物理ベースレンダリングを柔らかく説明してみる（４）

いよいよ鏡面反射BRDFのお話

　前回だいぶ寄り道しましたが、いよいよ鏡面反射BRDFのお話に入っていきます。現在のリアルタイムCGにおける物理ベースレンダリングでは、ディフューズ反射成分については、コスパの問題から正規化ランバートで済ませてしまう例もまだまだある、というお話を以前しました。

　物理ベースレンダリングの恩恵が分かりやすい意味で得られるのは、やはりスペキュラ（鏡面反射）成分についてでしょう。そのお話をしていきます。よく聞くGGXなどの単語も一体なんぞそれ、というのが今回の記事でわかってくることと思います。

　ただし、第1回冒頭でも書いたとおり、本記事はなんとなく手っ取り早くわかった気になりたい人向けの記事ですので、正確さや網羅性を犠牲にしています。内容でいえば他の方が書かれた記事の方がはるかに詳しいので、CGにある程度の自信がある方はそちらをご覧になった方が良いと思います。

現在の鏡面反射BRDFでの定石の式 - Torrance-Sparrowモデル

　いきなりぶっちゃけた話にしてしまいます。この定石が得られるまでに数多くのCG研究者の方々の努力や改善の系譜があったわけですが、それらは実際に各種の論文や技術発表資料などから参考文献リストを自分なりにたどっていくのが良いと思います（私も勉強中です）¹。
　とはいえ、闇雲にたどっていっても、よほどCGの勉強が好きな方でない限り、理解への壁は高いでしょう。

　手っ取り早く概要をつかみたいという方は、まずは現在の鏡面反射BRDFの定石（Torrance-Sparrowモデル）を覚えてしまいましょう。

f_{r,s} = \frac{DGF}{4(\vec{n}\cdot \vec{l})(\vec{n}\cdot \vec{v})}.

　ここで、
　$f_{r,s}$は、BRDFの関数（より広義のBSDFの中でも、反射を扱うBRDFを指すのでrがついていると思われます）であり、さらにスペキュラについてのBRDFであることを示すためにsがついています。
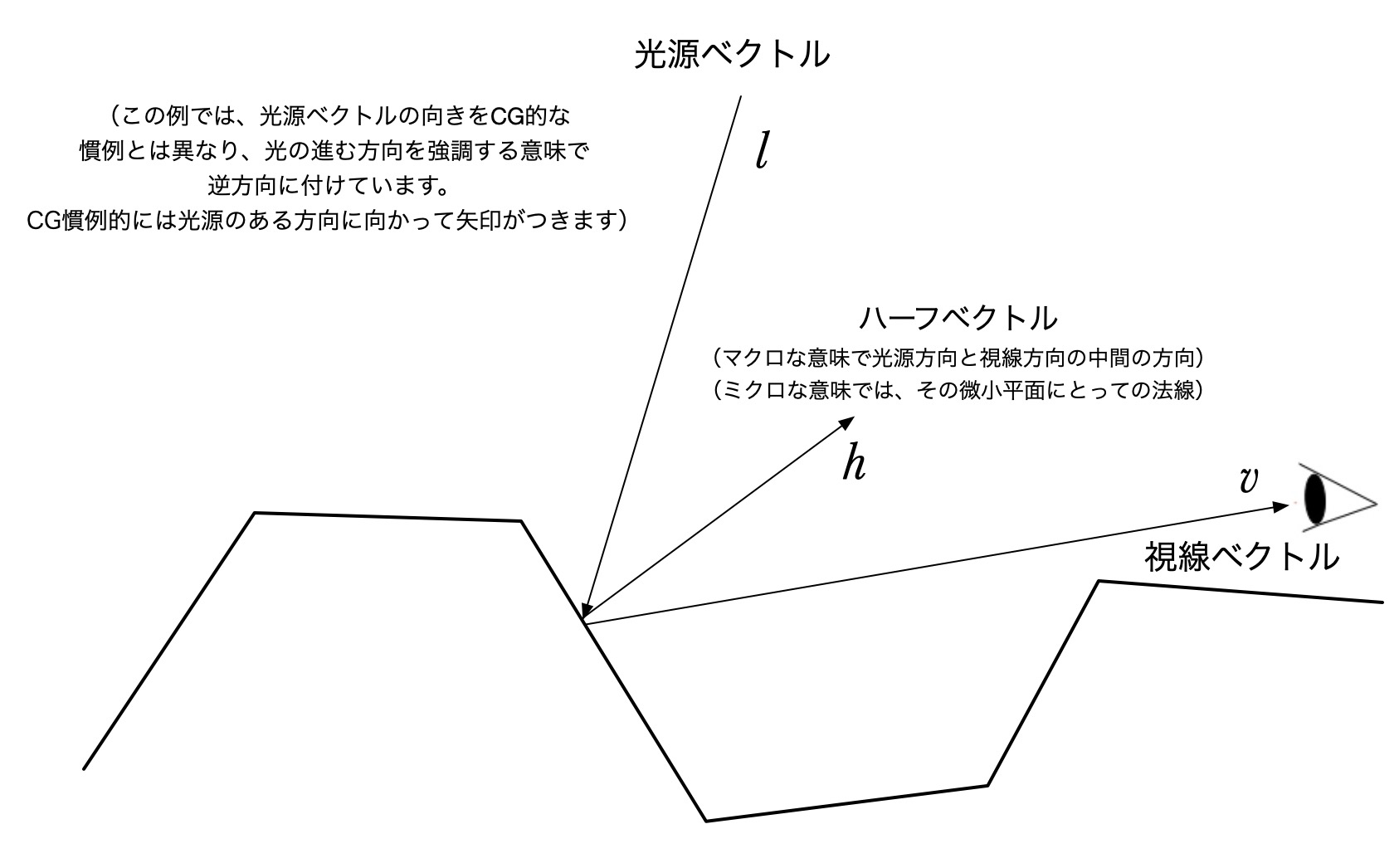
　$\vec{n}$は物体表面の法線（マイクロファセット法線ではなく、マクロな意味での物体表面の法線です。ノーマルマッピングを併用している場合は、ノーマルマップ後の法線を利用することになるでしょう）です。
　$\vec{l}$はライトベクトル、$\vec{v}$は視線ベクトルになります。$D$, $G$, $F$は後ほど説明します。

　記述の仕方によっては、以下のように書かれることもあると思いますが、意味は同じです。

f(x,\omega', \omega) = \frac{DGF}{4(\vec{n}\cdot \vec{\omega'})(\vec{n}\cdot \vec{\omega})}.

f(x,\omega_o, \omega_i) = \frac{DGF}{4(\vec{n}\cdot \vec{\omega_o})(\vec{n}\cdot \vec{\omega_i})}.

　このTorrance-Sparrowモデル²は光学分野で60年代後半に考案され、この定式をベースにコンピュータグラフィックス分野ではBlinnモデル³やCook-Torranceモデル⁴といった派生系が生まれました。
現在の物理ベースレンダリングにおいて、スペキュラ（鏡面反射）成分のBRDFについて議論する際は、実質的にこのTorrance-Sparrowモデルを前提として話がされることがほとんどだと思います。この式の形は覚えてしまいましょう。

　その上で、式の分子の部分である$D$, $G$, $F$についてこれから説明していきます。

D: 微小面法線分布関数（マイクロファセット法線分布関数）, NDF

　D項は微小面法線分布関数といいます。マイクロファセット法線分布関数、英語表記ではNDF(Normal Distribution Function)と書かれたりもします。

　これは、物体表面のミクロレベルの各微小平面の法線がどれくらい指定の方向を向いているか、という法線の分布を表す関数になります。ライティング計算において、法線が重要なのはご存知のとおりですね。ミクロスケールでも同様です。
　ただ、どの微小平面も様々な方向を向いているわけで、一つ一つ吟味するなどとてもやっていられません。そこで、だいたいの分布の傾向を数学的に関数で表すようにした、というわけなのですね。⁵

　このD項ですが、実際の式は一種類ではありません。CG研究者たちによって、実に様々な分布関数が提案されています。
　もともとのCook-Torranceの論文ではBeckmann分布という分布関数が提案されています。

D_{beckmann} = \frac{1}{m^2\cos^4\alpha} e^{-(\tan\alpha/m)^2}

　現在では、それとは別のGGX(Trowbridge-Retiz)という分布が使われることが多くなっています。確かに、物理ベースレンダリングのお話でGGXってよく聞きますね。ようやく出てきました。このGGX分布はWalterという方の論文（Cook-Torranceをベースに透過材料を表現するため、BSDFモデルを提案）で初めて「GGX」という表記で出てきたのですが、同様のモデルを過去にTrowbridge&Retizらも提案していたため、Trowbridge-Retiz分布とも呼ばれたり、両方併記されることが多いです。
　GGXが現在よく使われる理由は、そこそこの計算コストで、反射ローブにおけるそれなりの長いテールを維持できるからだそうです。反射ローブ？？　以前の記事の図を思い出してください。あんなのです。
　ようは、反射のピーク（反射が一番強い箇所）から離れた角度になればなるほど、反射の強さは急速に落ちていくのですが、離れた角度になってもすぐに完全に反射がなくなるのではなく、ある程度は反射が残ります。それをテールというのですが、それが長いということです。
こういうCG用語って、意外とその意味をわかりやすく説明しているケースってないですよね。困りますよね。ちなみにスペキュラスパイクは、反射のピークの突起を指します。誰か教えてくれなきゃそんなの分からんがな…。

　さて、GGXの式は以下のとおりです。

D(h) = \frac{\alpha^2}{\pi((\vec{n} \cdot \vec{h})^2(\alpha^2-1)+1)^2}.

　文献によっては以下のようにも書かれていますが、

D(h) = \frac{\chi^+ (\vec{n} \cdot \vec{h}) \alpha^2}{\pi((\vec{n} \cdot \vec{h})^2(\alpha^2-1)+1)^2}.

$\chi^+ (\vec{n} \cdot \vec{h})$は法線とハーフベクトルの内積が0以下なら0、0より大きければ1を表すステップ関数です。つまり、内積がゼロ以下のときは0にして全体の値がマイナスにならないようにしています。別の言い方をすると、マクロ面とマイクロ面が同じ側にある方向に対してのみ、マイクロ面が見えることを保証しています。

　$h$はハーフベクトルといい、ライトベクトルと視線ベクトルを足して正規化したベクトルです（より感覚的に言えば、光源方向と視線方向の中間の方向を指します）。つまり、各微小平面のうち、物体表面における（マクロな意味での）ハーフベクトルの方向を向いているものの割合が、視線方向に実際に反射する光の鏡面反射成分に寄与することを意味しています。
　どういうことか、以下の図でイメージしてみてください。（マクロ的な意味での）ハーフベクトルの方向を（法線が）向いている微小平面が、絵的に見ても反射に寄与するように見えるでしょう？　実際にそうなのです。

　さて、この簡略化された式はUnreal Engineの技術資料⁶で提案されたもので、この$\alpha$はユーザーが触るマテリアルパラメータとしての$roughness$（ラフネス、粗さ）を２乗した値になります。現在の多くのゲームエンジンやリアルタイム向けCGツールでは、この簡略化型の式で実装されていることが多いようです。
　このように、同じ分布の式でも、言及する論文や実装するエンジンなどによって、具体的な式の形が結構異なっているケースはよく見られます。どこかの記事やWikipediaなどで、「これこれの式はこれだー！」って書かれているのを、それそのままに受け取ると理解の半分しか得られないので注意しましょう（単純に細部に表記ミスがある場合だってあるかもしれません！）。

G: 幾何減衰項

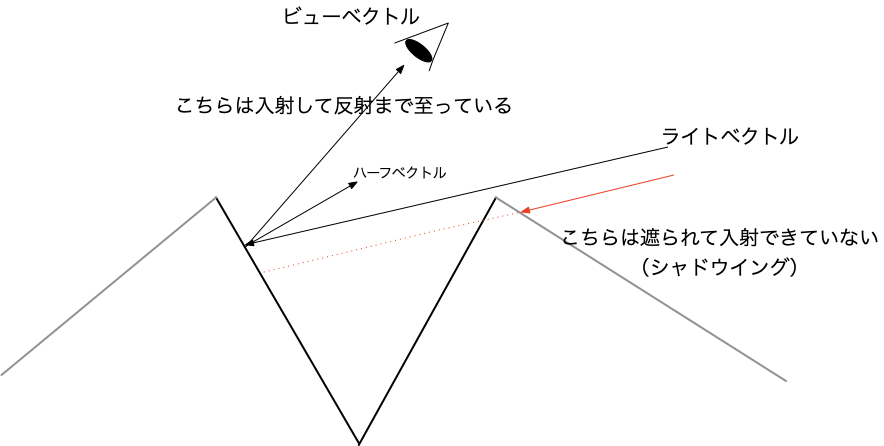
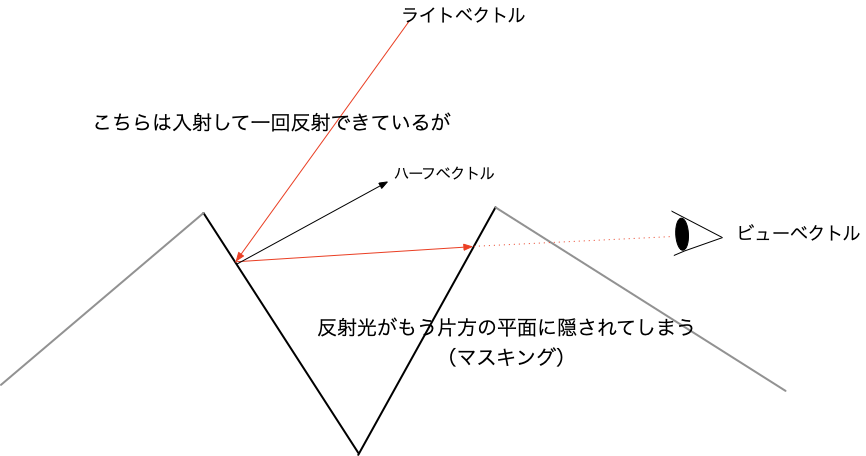
　このG項は幾何減衰項ともいい、マイクロファセット同士が光の反射経路を遮蔽する（ローカルオクルージョンとも呼ばれます）ことにより、失われてしまう光の反射成分（減衰）を考慮するものです。具体的な遮蔽のパターンとして、主にシャドウイングとマスキングがあります。

シャドウイング

マスキング

　このG項ですが、元々は物理学の分野で生まれたもののようです。この遮蔽構造のマイクロファセットモデル化にはいくつかの種類があり、主なものにV-cavityモデルとSmithモデルがあります。

V-cavityモデル

V-cavityモデルは前の図にもあった、シンメトリーな２つ平面の同士が織りなすV字型の谷の集まりと捉える考え方です。その形からV-cavity型などと呼ばれたりもします。

1967年にTorrance と Sparrowによって提案されたマイクロファセットモデルで、後にOren Nayar BRDFなどでもベースの考え方とされてきました。

Smithモデル

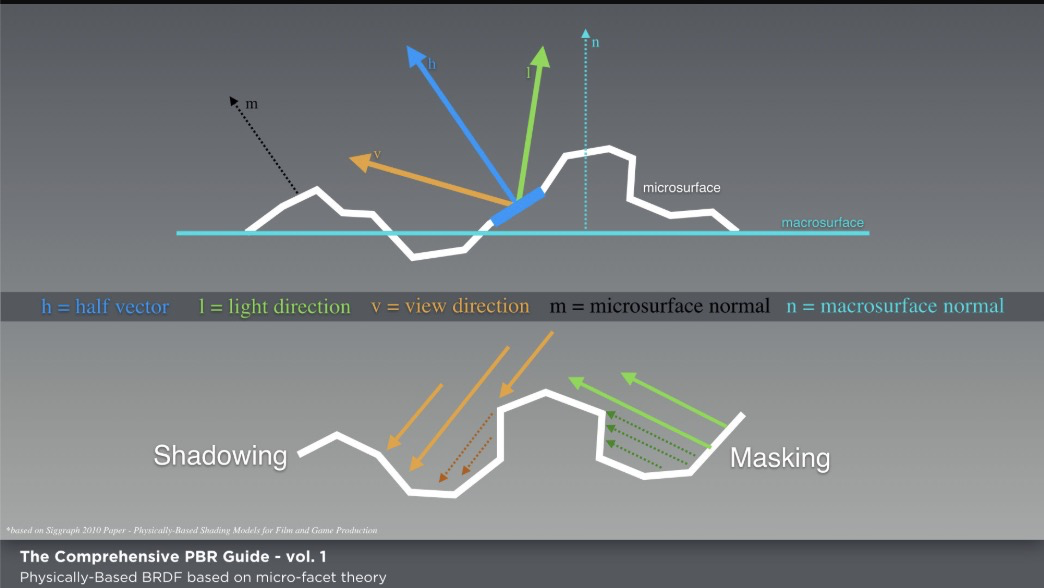
Wes McDermott「The Comprehensive PBR Guide by Allegorithmic - vol. 1 Light and Matter : The theory of Physically-Based Rendering and Shading」©Allegorithmic　より引用

今日では主にspecular BRDFを始めとして、こちらのSmithモデル⁷で考えることが多くなっているように思います。V字型というよりも、でこぼこ型とでもいいましょうか、ところどころV字的な部分もあると思いますが、より一般的な凹凸の様相を考えた形になります。

さらにCG分野においては、このシャドウイングとマスキングをあえて別々に取り扱い、その乗算で近似して表そうという考え方が出てきました。これをSeparable Masking and Shadowingといいます。

G(\vec{\omega}_i,\vec{\omega}_o) \approx G_1(\vec{\omega}_i) G_1(\vec{\omega}_o)

$G_1$は単方向シャドウイング関数と呼ばれます。Schlickという方は論文で、さらに簡略化した$G_1$を提案しました。これはよくSmithモデルのSchlick近似と呼ばれます。

k = roughness \cdot \sqrt{\frac{2}{\pi}} \\
G_{Schlick}(v) = \frac{n \cdot v}{(n \cdot v)(1-k) + k} \\
G_{Smith}(l,v,h) = G_{Schlick}(l) G_{Schlick}(v)

　近年ではさらに改善が進んでおり、今までのG項では隣り合うマイクロファセット同士の高さに一貫性がなかった（隣のマイクロファセットが極端に出っ張ったり引っ込んだりする場合があり得た）のを修正したHeight-Correlated Masking and Shadowing⁸というものの採用が増えています。これはSmith Joint Masking and Shadowing FunctionやSmith Joint GGXとも呼ばれるそうです。

　元の論文の式がわかりにくかったので、実際の実装例のコードを元にした式を以下に示します。

V(l,v,h) = \frac{0.5}{\Lambda_l+\Lambda_v} \\
\Lambda_l = \vec{n} \cdot \vec{v} \sqrt{(\vec{n} \cdot \vec{l})^2 \cdot (1.0 - \alpha^2) + \alpha^2} \\
\Lambda_v = \vec{n} \cdot \vec{l} \sqrt{(\vec{n} \cdot \vec{v})^2 \cdot (1.0 - \alpha^2) + \alpha^2} \\
\alpha = roughness^2

　ん？　$V$？ $G$じゃないの？　実装の仕方にもよると思うのですが、この場合の式では、鏡面反射BRDFは少し変形され、以下の形になりますので注意してください。

\displaylines{
f_{r,s} = DVF \\
V = \frac{G}{4(\vec{n}\cdot \vec{l})(\vec{n}\cdot \vec{v})}
}

F:フレネル項

　以前の記事で、拡散反射は物体表面で一度屈折して媒質中に入った光（の一部）がその対象となるという話をしたと思います。逆に、表面ですぐに反射した光が鏡面反射に該当することもお話しました。

　それは当然、BRDFでも考慮しなければなりません。それがこのフレネル項です。

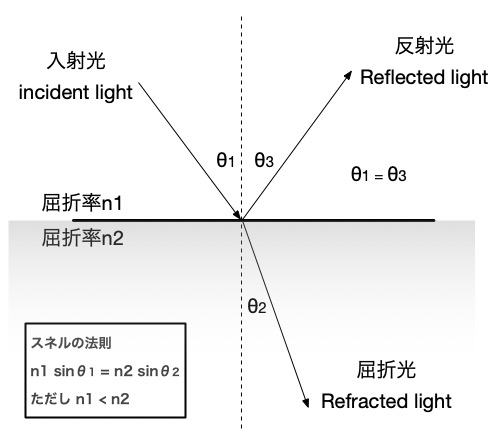
　フレネルのオリジナルの式は、光の偏光という現象を前提とした割と複雑な式になっており、リアルタイムCGでこれが直接使われることはほとんどありません。
　Schlickはこのフレネルの式を偏光を考えない場合で、オリジナルの結果に極力フィットするような近似式を提案⁹しました。現在では、こちらの近似式が使われることが多いです。

F(\vec n) = F_{0} + (1-F_{0})(1-(\vec l \cdot \vec n))^5.

ただし、通常マイクロファセットベースのスペキュラBRDFでは、内積部分に$(\vec l \cdot \vec n)$ではなくハーフベクトルを用いた$(\vec l \cdot \vec h)$としたバージョンが使われます。

F(\vec h) = F_{0} + (1-F_{0})(1-(\vec l \cdot \vec h))^5. \\
where \\ \vec h = \frac{\vec v + \vec l}{|\vec v + \vec l|}.

ちなみに、$(\vec l \cdot \vec h)$ではなく、$(\vec v \cdot \vec h)$としている場合も多くあります。

F(\vec h) = F_{0} + (1-F_{0})(1-(\vec v \cdot \vec h))^5.

いずれにしろ、スペキュラBRDFにおいては同じ意味です。なぜなら、$(\vec l \cdot \vec h)$も$(\vec v \cdot \vec h)$も、相手側のベクトル$\vec h$が$\vec l$と$\vec v$の中間の方向を示すので内積値が等しくなるからです。

$F_0$は、平面に垂直方向から光が入射した際の鏡面反射率になります。詳しくは今後の記事で説明しますが、物理ベースマテリアルのメタリックワークフローにおいては、メタリック１の領域にはベースカラーにこの$F_0$の値をいれることになります。

式全体を考える

　さて、$D$, $G$, $F$の中身を見てきましたが、物理ベースレンダリングの研究開発では、これらの各項にどのような関数を採用するか、制作する作品の特性に応じて検討することがよく行われます。そうして決まったこの３項をCook-Torranceの式に代入して考えればよいわけです。

f_{r,s} = \frac{DGF}{4(\vec{n}\cdot \vec{l})(\vec{n}\cdot \vec{v})}.

　さらに、拡散反射についても、例えばこちらは正規化ランバートで考えるとしましょう。

f_{r,d} = \frac{\rho_d}{\pi}

　拡散反射と鏡面反射を両方考える場合（殆どの場合、ライティングするときにはそうですよね）、両者を合算するわけですが、ただ単純に足してはいけません。以下のようにする必要があります。

f_{r} = f_{r,d} (1-F) + f_{r,s}

　$F$はフレネル項です。
　というのも、フレネルの法則から考えて、物体表面で屈折した光成分のみ、拡散反射の対象となりえるからです。$f_{r,s}F$としなくていいの？ と思われるかも知れませんが、Cook-Torranceの式を思い出してください。すでに内部にフレネル項がありますよね。だから外からさらに$F$をかけなくても大丈夫（むしろかけてはいけない）なのです。

ぶっちゃけ、実装ってどうやるの？

　上記を座学しても、いまいち腹落ち感がない、という方は多いでしょう。
　幸い、今はネット上で優れた物理ベースレンダリングの実装が多くあります。
　おすすめはKhronosによるglTFのPBRサンプルビューアーでしょう。最近公開された新版と旧版があり、旧版の方がシンプルな実装なので追いやすいと思います。README.mdの解説とフラグメントシェーダーのコードを交互に眺めてみると良いでしょう。
　今後の記事では、このサンプルビューアーのPBRシェーダーコードの読み解きなどもやっていければと思っています。
　ちなみに新版の方では、幾何減衰項にHeight-Correlated (Smith Joint) Masking and Shadowingが採用されています。

発展形

　この以下の物理ベースBRDFは、最も素朴な形と言っていいでしょう。

f_{r} = f_{r,d} (1-F) + f_{r,s}

　最近はレンダラーやゲームエンジンなどで、さらに複雑な複合BRDFが採用されています。有名なのはDisneyが発表したDisney Principled BRDFです。UnrealなどのゲームエンジンのスタンダードPBRマテリアルでは、このDisney Principled BRDFのサブセットに相当するものが採用されているケースが多いようです。複合BRDFは多くの研究機関やCGソフトウェア会社から様々なものが提案されています。上記の基本形に慣れたら、ぜひ皆さんも調べてみてください。

　多くのアドバンスドな複合BRDFに見られるパラメータ（BRDFレイヤー）には、例えば以下のものがあります。

クリアコート

車の塗装などがイメージしやすいと思います。本来の材質の上に、ワックスのような滑らかな塗装が塗布されたような材質は、工業製品を中心に私たちの暮らしの中に多く見られます。クリアコートはそうした表現に応えるためのBRDFレイヤーです。

(画像は @cx20 さんのgltf-testサイトにあるClearCoatTestモデルのBabylon.js版サンプルをキャプチャしたもの)

Sheen

ベルベットやソファーなど、布の生地の繊維が微細かつ特徴のある反射をもたらすことがあります。これは布地を表面を構成する繊維（ファイバー）の微細な束が、光に対して特徴的な散乱を起こさせることによります。この散乱をモデル化したのがSheenレイヤーです。

(https://github.com/KhronosGroup/glTF/tree/main/extensions/2.0/Khronos/KHR_materials_sheen より画像引用)

最近の研究

マイクロファセットの単一散乱モデルにおけるエネルギー損失の補填

　難しそうな見出しに、一体何のことだ？　とぎょっとされたかもしれません。
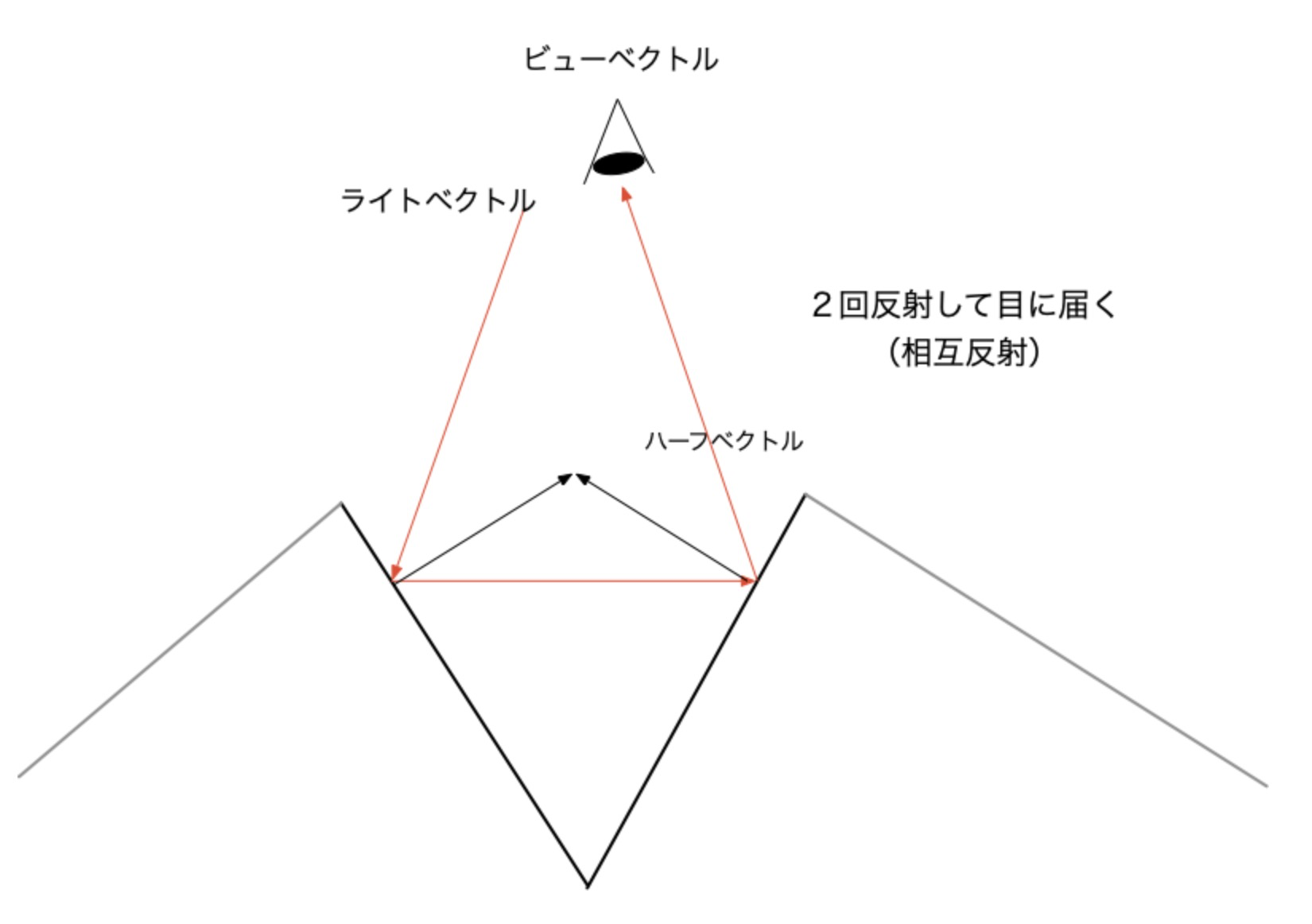
　これまでの既存の反射モデルには大きな問題が残されていました。マイクロファセット同士の相互作用（光の跳ね返り）が一度しか考慮されておらず、相互作用が複数回（多重散乱が）起きた結果、光がきちんと反射するケースを考慮できていないことです。
　下図は、複数回の散乱反射によって（マクロ的な意味でも）反射に成功するイメージ図です。

　この多重散乱による反射の成功（とそれを考慮していない反射モデルにおけるエネルギーの損失）は、ラフネス値が高い（つまり、ざらついた表面）のケースになるほど顕著だそうです。確かに、なんとなくイメージにあうような気がしますね。

　以下の２つの図は、Google Filamentレンダラーの技術資料からの引用です。単一散乱反射の方では、多重散乱反射のものに比べて、ラフネスの増加とともに実際にエネルギーの減少により、明らかに暗くなっていることがわかるかと思います。

Google Filament Document, 4.7.2 "Energy loss in specular reflectance"

　物理的により正確な品質を担保するため、その損失をなくさないといけないのですが、実際に多重散乱までまじめに取り扱うのは大変です。¹⁰

　そこで考え出されたのが、次の方法です。
　半球面全体の光を１（つまり、理想的な光で十分に満ちている）として、表面の鏡面反射を計算（拡散反射は考えない＝このときのBRDFのフレネル項は1.0＝完全鏡面反射とみなす）した結果、その半球面積分値は理想的には１になるはずです。この値はスペキュラ反射能または指向性アルベドと呼ばれています。
　しかし、実際は前述の損失があるため、１未満になります。１からこのスペキュラ反射能を引けば、損失の合計がわかります。その損失分をうまく補填するような追加のBRDF項を算出して加算することで、エネルギーロスの問題を解決してしまおうアイデアです。

　参考になる論文を挙げようと思ったのですが、少し古いものから新しいものまで複数出ているので、うまくまとめてあるGoogle Filamentレンダラーの技術資料における説明をご紹介します。

Google Filament Document, 4.7.2 "Energy loss in specular reflectance"

　この項は、主に事前計算されてテーブル化（リアルタイムCGでいうならテクスチャ化）されることが多いようですが、反射モデルが決まっている場合は、その加算項を数学的な近似式で与えてしまう場合もあるようです。

　また、リアルタイムレンダリングにおけるPBRではPunctual Light（ポイントライトなど）のケースに加え、IBL(Image based Lighting)における実装対応も別で考えなければいけません。
　ありがたいことに、最近ではIBLにおけるEnergy Conservation（エネルギー補填）向けに余計な追加の事前計算テーブル等の不要なより実用的な手法が登場しています¹¹。
　論文の情報だと取っ付きにくいという方は、以下のBruno Opsenica氏のブログ記事をご覧ください。具体的にIBLのシェーダーでどうすれば良いか、具体的なコードが示されています。

フレネル項によるディフューズレイヤーとスペキュラレイヤーの結合の正確性について

　より緻密な物理ベースレンダリングを考慮する場合、

f_{r} = f_{r,d} (1-F) + f_{r,s}

という線形補完的な結合モデルでは不十分な場合があるようです。この単純な混合によりエネルギー保存性が完全でない可能性があります。
Tri-Ace五反田らは、ディフューズフレネル項という、スペキュラフレネル項の$(\vec v \cdot \vec h)$を$(\vec l \cdot \vec n)$に置き換えたバージョンでディフューズ成分を(1 - F_diffuse)スケールすることで失われたエネルギーを担保する方法を提案しました。
http://simonstechblog.blogspot.com/2011/12/microfacet-brdf.html
http://renderwonk.com/publications/s2010-shading-course/gotanda/course_note_practical_implementation_at_triace.pdf

より緻密なモデルとしては、前述の指向性アルベドを利用したアプローチによりエネルギー保存を担保する方法が提案されています。
アドバンスドな内容になるため、とりいそぎ本記事では参考図書の該当箇所のみ紹介します。
「リアルタイムレンダリング第４版」（日本語版）の「9.9.3 滑らかなサーフェスの表面下モデル」の9.65式あたりの解説を読んでください。

しかし、通常のリアルタイムレンダリングではそこまで厳密に扱うのは実装コストや計算コストに見合わないことも多く、最初に紹介した

f_{r} = f_{r,d} (1-F) + f_{r,s}

で済ませることが多いようです。実際、物理ベースレンダリングを採用した3Dファイルフォーマットの１つ、glTFの仕様書の付録のBRDF実装の章では、fresnel_mixという上記の線形補完に相当する関数でディフューズBRDFとスペキュラBRDFを結合しています。

光の反射・散乱などの光学現象のより厳密な理解について

　私のこれまでの説明は手っ取り早くシェーダーでPBRレンダリングを実装するための浅い知識に過ぎません。
　光の性質と物体・媒質との相互作用には、我々が知らないもっと深い詳細があります。その詳細な世界について概念レベルでも触れておくと良いでしょう。

• Karmaシェーディング理論 | SideFX
• Introduction to “Physically Based Shading in Theory and Practice”

　光の性質と媒質との相互作用では多くの要因が働き、また光には粒子と波の二つの性質があるため、これらを説明するときの切り口によっては厳密さを担保することが難しいようです。こうした資料は複数を参照してバランスをとった方が良いでしょう（SideFXのサイト動画の説明の切り口については、以前私がSNSでシェアしたところ、「光の粒子性に頼った説明になり過ぎているのでは」といったご指摘をいただいたこともありました）

おわりに

　ようやく鏡面反射BRDFを取り上げることができました。だいぶざっくりになってしまいましたが。
　次は、ずっと座学もあれなので、glTFのPBRサンプルビューアーのコードの解説などできればと考えています。実装のレイヤーで理解できると、おそらくようやく腹落ち感がでてくるでしょうから。
　その次は、メタリック・ラフネスワークフローの先駆けである、Disney Principled BRDF（のサブセット）のお話をいたしましょうか。ゲームエンジンなどではそれに倣っている物が多いので、実際に皆さんにとっても有益かと思います。
　あればかりが有名になってしまって、それが全てでは決してないんですが…。

追記：
　結局、第５回は「光の単位について」になりました。なんでこう想定通りに進まないのか…。

1. Pocol, 「Direct3D12ゲームグラフィックス実践ガイド」 ↩

2. K.E.Torrance & E.M.Sparrow, "Theory for Off-Specular Reflection From Roughened Surfaces", 1966 ↩

3. James F. Blinn, "Models of Light Reflection for Computer Synthesized Pictures", 1977 ↩

4. Robert L. Cook&Kenneth E. Torrance, "A Reflectance Model for Computer Graphics", 1982 ↩

5. 関数は関数でも、このD項や全体のBRDFは確率密度関数というカテゴリに入ります（たまに「確率分布関数」と呼んでしまう方がいますが、「確率密度関数」と「確率分布関数」は別物です）。グラフにした場合、その関数曲線のある区間における面積が確率になります。つまり、BRDFは（光とともに）積分計算されることで答えとなる出射光の量がわかるわけです。BRDFはそれ自体では測ることができない微分関数といえます。 ↩

6. Brian Karis, Epic Games, "Real Shading in Unreal Engine 4", 2013 ↩

7. [SMITH, B. 1967] Geometrical shadowing of a random rough surface. IEEE Trans. on Antennas and Propagation 15, 668–671. ↩

8. Christophe Schlick, "An Inexpensive BRDF Model for Physically based Rendering", 1994 ↩

9. Heitz, E. Understanding the Masking-Shadowing Function, 2014 ↩

10. Eric Heitz, Johannes Hanika, Eugene d’Eon and Carsten Dachsbacher, "Multiple-scattering microfacet BSDFs with the Smith model", 2016 ↩

11. Carmelo J. Fdez-Aguera, "A Multiple-Scattering Microfacet Model for Real-Time Image-based Lighting"Journal of Computer Graphics Techniques Vol. 8, No. 1, 2019 ↩