概要
この記事は前回書いた記事「ゼロから作るDeepLearning -Pythonで学ぶディープラーニングの理論と実装-を読んだメモ ~パーセプトロン編~」の続編です。
今回話題にする「ニューラルネットワーク」のベースとなった「パーセプトロン」について書いています。
そちらも合わせてご覧ください。
前回は「パーセプトロン」という考え方、仕組みについて触れました。
今回はそれを発展させた「ニューラルネットワーク」について書いていきたいと思います。
ちなみに、ニューラルネットワークは最近話題の「ディープラーニング」のベースとなっているものの、定義的にはニューラルネットワーク自体がディープラーニングを指すものではないようです。
ニューラルネットワークを多層にして(つまり層を「深く」して)学習を強化することを「ディープラーニング」と呼ぶようです。
(とはいえ、多層にする方法は色々ありますが基本の部分はほとんど変わらないので、ニューラルネットワークを学ぶことでディープラーニングについてだいぶ理解が進むと思います)
なお、前回の記事同様、以下の書籍を読んだ上での個人的なメモ、備忘録となります。
ある程度の誤解、意訳などがあることを予め了承の上お読みください。
ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装
ニューラルネットワークとは
ニューラルネットワークを図で表すと以下のようになります。
上の○の部分はニューロンと呼ばれます。
そして一番左の層を「入力層」、中間を「中間層」、最後が「出力層」となります。
コンピュータになにかしらの入力を与え、それに基づく結果を得るのが機械学習です。
つまりコンピュータへの入力が入力層に与えられ、中間層を通り最後に出力層へとつながるわけです。
このことから、中間層を「隠れ層」と呼ぶこともあります。
入力と出力は人から見ることができますが、中間層は人から見ることができないためにそう呼ばれます。
図のように、ニューラルネットワークはニューロン(ノード)が層ごとに接続され、入力信号を「なにがしかの計算をした後に」出力層に送る構造を示しています。
そしてこのことは、前回の記事で触れたパーセプトロンとまったく同じ構造をしていることになります。
パーセプトロンの復習
パーセプトロンと同様、ニューラルネットワークも信号が各層を流れていきます。
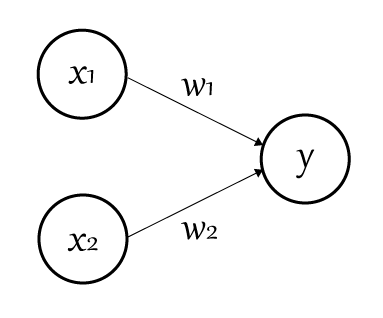
前回書いた記事からパーセプトロンの図を再掲すると以下のような形になっていました。
$x_1$と$x_2$にそれぞれ重み$w_1$、$w_2$をかけ合わせたものの合計が出力($y$)に伝わる様子です。
式で表すと以下です。
\begin{eqnarray}
y {=}
\begin{cases}
0 & : (b + w_1 x_1 + w_2 x_2) \leq 0 \\\
1 & : (b + w_1 x_1 + w_2 x_2) > 0
\end{cases}
\end{eqnarray}
ここで$b$は「バイアス」、つまり「どれだけニューロンが発火しやすいか」を表します。
そして$w_n$は「重み」です。これは各ニューロンの重要性を表すパラメータです。
重要度が高いニューロンほど重みが強くなり、より発火しやすさに貢献する、というわけですね。
ちなみに、上の図では上記の「バイアス」の部分が図示されていません。
それを含めてあらためて図にすると以下のように表すことができます。
上の図ではバイアスの部分のニューロンを、常に$1$を出力する特別なニューロンとして表現しています。
そのため、網掛けをして差別化をしています。
実際の計算では、「1 * b」となり、バイアスの値によって出力結果に影響を与えることが見て取れます。
これを元に、上記式をよりシンプルな形で表現してみます。
場合分けの動作(0を超えたら1を出力し、そうでなければ0を出力する動作)をひとつの関数で表すとして、
y = h(b + w_1 x_1 + w_2 x_2)
\begin{eqnarray}
h(x) {=}
\begin{cases}
0 & (x ≤ 0) \\
1 & (x > 0)
\end{cases}
\end{eqnarray}
ここで$h(x)$は上記の通り、入力に応じて0か1を出力する関数です。
つまり、入力信号の総和が$h(x)$という関数によって変換され、その変換された値が出力$y$になる、ということです。
活性化関数
上の関数の説明を読めばピンと来ると思いますが、前述の$h(x)$のことを一般に「活性化関数」と呼びます。
「活性化」という名前が意味する通り、入力によって与えられた信号が「活性化するか否か」を判断する関数、というわけです。
詳細は後述しますが、活性化関数に用いられる関数は、入力に対して0〜1の範囲で結果を返す関数となります。(ただ、最近では(後述の)ReLU関数を用いることが増えているそうで、この関数は閾値以下は0を、それ以外は入力をそのまま返す関数です)
基本的に活性化関数は「非線形」の関数であればいいようです。
(線形性の関数だと、隠れ層の計算が係数などを調整することで入力層と出力層だけでも計算が行えてしまい、隠れ層の意味がなくなる、というのが理由のようです)
なので、非線形の関数であれば色々利用することができます。(が、一般的に用いられる関数、より最適な関数はある程度決まっているようです)
余談。
ちなみに、自然数の指数関数であるexp関数を利用すると比較的シンプルに0〜1の値を得ることができます。
(注:活性化関数としては適していません)
y = 1 - exp(-x)
上記のyをグラフにプロットすると以下の結果が得られます。
xが増加するに従って急激にカーブを描いて1に近づいていき、でも1を超えずに徐々にカーブがゆるくなっていく様子が分かるかと思います。
こうした「0〜1」を返す関数は意外とあるので、色々調べてみても面白いかもしれません。
閑話休題。
活性化関数は、実はパーセプトロンでも利用していました。
その関数は「とある数値以下なら0を、それを超えたら1を出力する」という関数です。
これは「ステップ関数」と呼ばれます。
式にすると以下のように表されます。
\begin{eqnarray}
h(x){=}
\begin{cases}
0 & : x \leq n \\\
1 & : x > n
\end{cases}
\end{eqnarray}
Wikipediaから画像を引用させてもらうと以下のような形の関数です。
図を見てもらうと分かりますが、グラフがステップ(階段)のようになっているのが分かるかと思います。
これが「ステップ関数」と呼ばれる所以ですね。
さて、ニューラルネットワークではこの活性化関数をもっと柔軟なものに置き換えていきます。
ステップ関数では「0か1か」という、とてもデジタルな判断しか行なえません。
しかし、今求めているのは「人間のように」0か1かではなく、0.5などもありえる判断を行う仕組みです。
そのためにはステップ関数では都合が悪いのですね。
シグモイド関数
上記のように、パーセプトロンではステップ関数を活性化関数として利用していました。
ニューラルネットワークではここを変更していきます。
よく使われる関数のひとつに「シグモイド関数」というものがあります。
まず式にして見ると、以下の形で表される関数です。
h(x) = \frac{1}{1 + exp(-x)}
なお、$exp(-x)$は$e^{-x}$を表します。
$e$はネイピア数(自然数)で、$2.7182...$と続く数字です。
$e^x$を微分した結果が$e^x$になるという特性があります。
少し前に書いた「[DeepLearning] 計算グラフについて理解する」で図解した画像を再掲すると、シグモイド関数が描くグラフは以下のようになります。

ステップ関数をなめらかにしたような関数になっているのが分かるかと思います。
(そういえば、スムースステップ関数も似たような形ですね)
ReLU関数
書籍をさらに読み進めていくと、最近のディープラーニングの世界では、シグモイド関数ではなくこの「ReLU関数」が用いられることが多いそうです。
この関数をグラフにしてみると以下のような形になります。

図で表される通り、特定の値以下は0を、それ以外は入力の値をそのまま出力する、という関数になっています。
式としても表しておくと以下のようになります。
\begin{eqnarray}
h(x){=}
\begin{cases}
x & : x > 0 \\\
0 & : x ≤ 0
\end{cases}
\end{eqnarray}
内容自体はシンプルなのであまり説明はいらないかと思います。
ニューラルネットワークの実装
実装と見出しを書いておきながら、あくまでイメージ的な解説にとどめます。
実際に動くまでの実装は載せません。
詳細を知りたい方は書籍を御覧ください。
ここではニューラルネットワーク自体がどういうふうに実装され、実行されるのか、という「雰囲気」を感じ取ってもらうのが目的です。
(というか、自分自身、イチからすべてを構築できるほど理解していないので、動くものを作ろうとすると書籍で解説されているコードのほぼコピーになってしまうので・・・)
「層」を定義する
パーセプトロンと同様、ニューラルネットワークも「層」を重ねることでものごとを認識、推測、判断していきます。
そのため構造的にはパーセプトロンとほぼ変わらないグラフを形成します。
図にすると以下のようになります。
ご覧のように、冒頭で紹介したパーセプトロンの図と似た形になっているのが分かるかと思います。(入力があって重みがあり、出力につながる)
そして中間の「隠れ層」に記載されているのが「活性化関数」です。
出力層で使われる関数
パーセプトロンと異なる点としては最後の「出力層」に記述されているソフトマックス関数と恒等関数でしょう。
これは、ニューラルネットワークの出力をどう扱うか、を決定するものです。
通常、(後述の)ニューラルネットワークの学習では、教師データと訓練データを使い、実際に出力された結果を「ソフトマックス関数」で加工したものを利用します。
一方、学習が終わり、実際の推論を行う段になった場合には恒等関数が使われ、コンピュータが推論した結果をそのまま利用します。
恒等関数とソフトマックス関数
実は恒等関数は「なにもしない」関数です。
式にすると、
f(x) = x
入力をそのまま出力するだけの関数ですね。
なので推論時は、各層を経て計算された結果をそのまま利用する、というわけです。
一方、ソフトマックス関数は以下のような式になります。
y_k = \frac{exp(a_k)}{\sum_{i=1}^{n}exp(a_i) }
計算中の層の入力の$exp$関数の結果を、すべての層の$exp$の計算結果を合計したもので割ったものが最終的な出力となる関数です。
コンピュータの限界
ちなみに、上記のソフトマックス関数、式としては問題ないのですが、指数関数を利用しているためその結果は膨大なものになる可能性があります。
そのため、コンピュータが扱える数値の上限を簡単に超えてしまいます。(64bitの倍精度浮動小数点でさえも)
なので、それを防ぐために以下のように少し式を変形します。
\begin{eqnarray}
y_k = \frac{exp(a_k)}{\sum_{i=1}^{n}exp(a_i) }
&=& \frac{C exp(a_k)}{C \sum_{i=1}^{n}exp(a_i) } \\
&=& \frac{exp(a_k + log C)}{\sum_{i=1}^{n}exp(a_i + log C) } \\
&=& \frac{exp(a_k + log C')}{\sum_{i=1}^{n}exp(a_i + log C') } \\
\end{eqnarray}
まず最初の式の変形は、分子・分母ともに定数$C$を掛けたものです。
分子・分母に同じ数を掛けた結果は変わらないのでここは問題ありませんね。
そして次の式では、その定数を$exp$関数の中に入れています。
$exp$関数は、ネイピア数$e$の指数関数でした。
対して、自然数を底とする対数$log$は、引数の値となる指数部分の値を求める関数です。
そのため、$exp$関数の中に入れる場合はその逆数的な対数を取って入れることで整合性を保っているわけです。
そして最後。
最後は、その$log C$を定数$C'$として表しています。
これはつまりは、$exp$関数の中に任意の値を加算しても、出力結果が変わらないことを表しているのです。
このことを利用して、実際の実装では$exp$関数の引数から、「ある数字」を減算(マイナス値を加算)することで、指数関数の急激な増加を抑える制御を行います。
書籍によれば、一般的には$a_i$の中で一番大きな数値を引くと書いてあります。
これらを踏まえて、実際の実装(Pythonコード)を示すと以下のようになります。
書籍を参考にさせてもらうと、
a = np.array([1010, 1000, 990])
# np.exp(a) / np.sum(np.exp(a)) # これをそのまま計算すると
# array([nan, nan, nan]) # NaNになって不定となってしまう
c = np.max(a) # 1010
np.exp(a - c) / np.sum(exp(a - c))
# array([9,99954600e-01, 4.53978686e-05, 2.06106005e-09])
ニューラルネットワークの学習
パーセプトロンとの違いとしてステップ関数以外の活性化関数について見てきました。
そしてパーセプトロンとの一番の違いはニューラルネットワークの学習にあります。
機械学習のひとつであるディープラーニング。(そのベースとなるニューラルネットワーク)
機械「学習」と名がつく通り、人の手によって設定されるものではなく、自動的に物事を「学習」していく仕組みが必要です。
ということで、ディープラーニングを学ぶのに必須となる「学習」について見ていきましょう。
学習アルゴリズムの手順
学習アルゴリズムの手順について、本から引用させていただくと簡単には以下のようなフローになります。
前提
ニューラルネットワークは、適応可能な重みとバイアスがあり、この重みとバイアスを訓練データに適応するように調整することを「学習」と呼ぶ。ニューラルネットワークの学習は次の4つの手順で行う
ステップ1(ミニバッチ)
訓練データの中からランダムに一部のデータを選び出す。その選ばれたデータをミニバッチと言い、ここでは、そのミニバッチの損失関数の値を減らすことを目的とするステップ2(勾配の算出)
ミニバッチの損失関数を減らすために、各重みパラメータの勾配を求める。勾配は、損失関数の値を最も減らす方向を示す。ステップ3(パラメータの更新)
重みパラメータを勾配方向に微小量だけ更新する。ステップ4(繰り返す)
ステップ1、ステップ2、ステップ3を繰り返す。
ここで登場した「重み」と「バイアス」はパーセプトロンの復習のところで解説したものと同じものです。
なので重みとバアイスについての解説は不要でしょう。
重みとバイアスの学習
ニューラルネットワークを学ぶ上で重要になるのがこの重みとバイアスの学習です。
ニューラルネットワークが行っていることはこのふたつのパラメータ----重みとバイアス----を適正な値に調整していくこと。
そしてこれを「学習」と呼んでいるわけです。
パーセプトロンの解説でも書いた通り、このパラメータさえ適切な値に設定することができれば、コンピュータは人間と同じように物事を判断することができるようになります。
しかし、「適切な値にできれば」と一言で言ってもそれは容易なことではありません。
実際のところ、ディープラーニングと呼ばれる深い階層を持つネットワークを学習させようとすると数万、数百万というパラメータが必要になるそうです。
これを人の手でやっていくのはとてもじゃないですが現実的ではありません。
しかし昨今のPCの性能向上、そして理論の構築により現実的な時間でこれを計算できるようになってきた、というのがディープラーニングが隆盛を始めたきっかけのようです。
(さらに最近ではGPUを利用した計算あったり、Googleがディープラーニング用のGPUを開発したり、といったことまで出てきています)
しかしながら、ディープラーニングを理解する上では、この膨大なパラメータをなにがしかの方法を用いて適切に行うことが「学習する」ということとイコールだと考えてもらっていいと思います。
勾配の算出(パラメータの調整)
前述のように、ニューラルネットワークはバイアスと重み付けを適切に学習(調整)していき、結果として高度な認識を行う技術だということは解説しました。
ではその学習はどう行うのか。
その具体的な内容に入る前に、少しだけたとえ話を。
想像してみてください。
あなたは今、山道で遭難して地図もなにもない状態で当てもなく山の中を歩いています。
山に入る前の知識として、谷に向かっていけば村があったことを覚えています。
今、あなたが立っている場所から目的の「谷」に向かうにはどうしたらいいでしょうか。
答えは「分かりません」。
しかしなにも行動しなければ待つのは死だけです。
なのでなにかしら行動に移すはずですよね。そして「谷に村がある」ということをヒントに移動を開始するわけですから、とにかく「今いる位置より下る」方向に移動しようと考えるのが自然です。
もちろん、山は起伏があるので今いる位置から登ることがゴールかもしれません。(登った先の起伏の先に谷があるかもしれませんよね?)
しかし、地図がない以上、「下る」ことしか選択するすべはありません。
つまり、「とにかく下ることが正解に近づくだろう」という前提のもと行動する、というわけです。
・・・
これが、ディープラーニングでの「勾配」を利用した学習パラメータの最適化(学習)の概念です。
つまり、とにかく数値的に勾配が下っているところを探し、そちらに移動していくと学習が進む、と仮定して処理をしていくのです。
「人間」が調整する「ハイパーパラメータ」
仮にその方向が間違っていた場合は学習が一向に進まない、という自体ももちろんあります。
そこで「ハイパーパラメータ」と呼ばれる特殊なパラメータを人間が用いて「どれくらい移動するのか」「どの方向に進むべきなのか」の学習状況を補正していくのです。
(現状は)なにからなにまですべて自動で学べるわけではなく、あくまで人間がサポートして最適な答えを見つけ出す手助けをしてやる必要がある、というわけなんですね。
さて、この学習法(勾配を求めて最適化していく)ですが、いくつかのアルゴリズムがあり、それをまとめて「勾配降下法」と読んでいるようです。
いくつかあるアルゴリズムについては以下の記事がとてもまとまっているのでオススメです。
パラメータの更新
ディープラーニングの最後のステップとして「パラメータの更新」があります。
ここでのパラメータは「重み」と「バイアス」です。
勾配降下法によって算出された勾配を手がかりに、パラメータを勾配方向に微小量だけ更新します。
この「微小量」がどれくらいかは、前述のハイパーパラメータに寄ります。
ハイパーパラメータを適切に設定しないと勾配方向への更新によって訓練が適切に行われず、パラメータが発散してしまったり、といった問題が出てきます。
なのでハイパーパラメータの設定が重要なんですね。
損失関数
パラメータは勾配降下法によって最適な値を求めて調整していく、ということを説明しました。
さて、では。そもそも「最適な値」とはなんでしょうか?
なにを持って最適とし、なにを持って勾配を求めるのでしょうか。
その答えが「損失関数」です。
ニューラルネットワークではあるひとつの指標を元に最適な値を探します。
その指標を表すのが損失関数です。
損失関数は任意の関数を取ることができます。
そして書籍によると、関数には「2乗和誤差」と「交差エントロピー誤差」を利用するのが一般的なようです。
損失関数の結果の意味
ちなみに、損失関数の結果の意味するところは「認識精度の悪さ」だそうです。
「どれだけ精度が高いか」ではない点が面白いですよね。
ただ、「精度の悪さ」はマイナスを掛けて反転することで「どれだけ精度が高いか」を意味することもできるので、本質的には同じことを言っているわけです。
さて、では前述のふたつの関数について見ていきましょう。
2乗和誤差(mean squared error)
2乗和誤差とは、誤差の2乗の和を用いて値を求める関数です。
最小二乗法や標準偏差などでも用いられる、誤差の2乗を評価するものですね。
以前、「[数学] 最小二乗平面をプログラムで求める」という記事を書きました。
ここでも2乗を扱っています。
なぜ2乗を扱うかというと、「とある値」の2乗は、「とある値」が大きい場合はより大きく、小さい場合はより小さくなります。
そのため、標準偏差や分散などを求める際にばらつきを求める指標になる、というわけです。
(おそらく、そうした理由から今回の2乗和誤差を損失関数として利用しているのだと思います)
式にすると以下のように表されます。
E = \frac{1}{2} \sum_{k}(y_k - t_k)^2
ここで、$y_k$はニューラルネットワークによって算出された値、$t_k$は教師データを表します。
つまり、教師データ(要は正解データ)との誤差がすべて0なら100%正しい認識をしている、というわけです。
(損失関数は「精度の悪さ」を示す指標です。それが「0」ということは「精度の悪さがない」ということですよね)
しかしながら、学習途中ではその誤差は大きくなります。
そしてその2乗の和を取ることで、「どれくらい精度が悪いか」を判断している、というわけですね。
交差エントロピー誤差(cross entropy error)
もうひとつの損失関数が「交差エントロピー誤差」です。
式にすると以下のようになります。
E = -\sum_{k} t_k log y_k
ここで、$log$は底が$e$の自然対数($log$)を表します。
また、2乗和誤差の場合と異なり、ここでは$t_k$は正解ラベルです。
正解ラベルとは、正解となるインデックスが1でそれ以外は0となる表現です。(one-hot表現と言います)
例えば、分類対象が4つあったとすると、正解インデックスの表現は、仮に1番目が正解なら「1 0 0 0」と表現されます。
また仮に2番目なら「0 1 0 0」ですね。
つまり、そのラベルと$log y_k$を掛け算するということは、「正解ラベルの値だけが採用される」という意味です。
(0を掛ければどんな値も0になる)
そしてそれを合計することで「精度の悪さ」の値が算出できるわけです。
ちなみになぜそうなるかと言うと、採用された値が「小さければ」どんなに合計しても大きな値にはなりません。
そして$log y_k$は、ニューラルネットワークが算出した値が1に近いほど(つまり正解に近いほど)0に近づく関数です。
分かりやすくするためにグラフにしてみると以下のような曲線となります。

x軸が0から1の値を取り、それが1に近づくにつれて結果のy軸の値が0に近づいていくのが分かるかと思います。
(ちなみに算出される値は「マイナス」値です。そのため、合計した値にマイナスを掛けて値を反転しています。損失関数の示す値は「精度の悪さ」です)
なぜ損失関数を使うのか?
損失関数は「精度の悪さ」を計算するものでした。
しかし、本来得たい結果は「いかに正しい認識をするか」です。
であれば、「精度の良さ」を指標にしたほうがいいようにも思います。
でもそれではダメなのです。
損失関数で「精度の悪さ」を計算し、それを微分することで(つまり勾配を求めることで)正しい値に調整していくのが「学習」だと説明しました。
もし「精度の良さ」を指標にしてしまうと、徐々に勾配がなくなり結果としてパラメータの調整がされなくなってしまう、というのが理由です。
参考にした本から引用させてもらうと以下のように説明されています。
ニューラルネットワークの学習の際に、認識精度を "指標" にしてはいけない。
その理由は、認識精度を指標にすると、パラメータの微分がほとんどの場所で0になってしまうからである。
そのために、「精度の悪さ」を計算する損失関数を導入している、というわけなんですね。
学習(勾配計算)の最適化手法
今回の記事では、まだ自分でディープラーニングを構築できるほど理解が進んでいないのでコードなど実装周りについては解説しません。
(でないと書籍のコピー以上のものができないので)
実装の詳細に関してはぜひ、書籍を手に取ってみてください。
実装の概要だけを書いておくと、学習には「勾配」を用いると解説しました。
勾配を求めるというと偏微分を思い出します。
ちなみに、偏微分が勾配を表すイメージについては以前記事にしたので興味がある方は読んでみてください。
完全に余談ですが、レイマーチングなどでもこの偏微分が勾配を表すことを使って法線を求めたりしますね。
閑話休題。
つまり、すべての入力に対して偏微分を行い、その結果(=勾配)を利用してパラメータを調整していく、というのが学習の大まかな流れです。
通常の計算方法
まずはどんなことを行うのかのイメージだけを掴んでもらうために、書籍から該当コードを引用させていただくと、大まかには以下のような実装になります。
def numerical_gradient(f, x):
h = 1e-4 # 0.0001
grad = np.zeros_like(x) # xと同じ形状の配列を生成
for idx in range(x.size):
tmp_val = x[idx]
# f(x + h)の計算
x[idx] = tmp_val + h
fx_h1 = f(x)
# f(x - h)の計算
x[idx] = tmp_val - h
fx_h2 = f(x)
grad[idx] = (fx_h1 - fx_h2) / (h * 2)
x[idx] = tmp_val # 値をもとに戻す
return grad
ここで行っていることは比較的シンプルです。
入力値としてのxはnumpyの配列です。つまり、複数パラメータの各値が入っています。
言い換えれば、x.size個の変数($x_1, x_2, ... x_n$)が格納された配列と考えてください。
そしてそれをforループで回して、それぞれの変数を加工しています。
加工はhだけ増減させ、その状態で関数fを実行しその結果を差分で割っています。
これはまさに微分の処理ですね。
こんなやつ↓
\lim_{x \to a} \frac{f(x) - f(a)}{x - a} = \lim_{\Delta x \to 0} \frac{f(a + \Delta x) - f(a)}{\Delta x}
そして、forループで対象しているのは「ひとつの変数」のみです。
ひとつの変数だけを対象に、それ以外の変数を定数とみなして微分するのが偏微分なので、ここではまさに偏微分が行われている、というわけなんですね。
そしてその結果の配列がまさに求めたい「勾配(=grad)」になっている、と。
処理自体はシンプルなので分かりやすいでしょう。
ただ気になる点があると思います。
仮に、入力されたxの(つまりパラメータの)数が膨大だったらどうなるでしょう?(例えば数百万個レベル)
想像したくないですが、相当な処理負荷になることは目に見えています。
微分対象とする関数が複雑ならば、それはそれは処理時間がかかってしまうことになってしまいます。
ただ、概念的にはこれ以上のことはしていないのも事実です。
次の節ではその最適化手法としての「誤差逆伝播法」について触れます。
誤差逆伝播法
前述のように、ディープラーニングでの学習には「勾配降下法」と呼ばれる方法でパラメータを最適化していくのでした。
そして勾配を求める方法は「偏微分」でしたね。
しかし、すでに触れたように偏微分を真面目に計算してしまうと計算回数が膨大なものとなってしまいます。
これは単純に計算負荷の増大を招き、学習に数時間、それどころか数日レベルでかかることも当たり前のようです。
なので、この微分計算、つまり誤差計算をなんとかして最適化し計算を早く行いたいわけです。
そこで登場するのが表題の「誤差逆伝播法」というわけです。
計算グラフ
書籍によると、この誤差逆伝搬法を学ぶのには「数式」によるものと「計算グラフ」によるものとがあるそうです。
一般的な書籍は数式から入るようなのですが、分かりやすさとしては計算グラフのほうが視覚化できて分かりやすいという理由から、説明を「計算グラフ」で行っています。
そのため、ここでも計算グラフについて取り上げておきます。
計算グラフとは
計算グラフとは、計算の過程をグラフで「視覚化」して表したものです。
計算グラフは複数の「ノード」と「エッジ」によって表現されます。
(エッジはノード間をつなぐ直線として表されます)
図にすると以下のイメージ。
なお、計算グラフに関してはこれはこれで長くなってしまいそうだったので、それだけを抜き出して別記事にしたのでそちらをご覧ください。
詳細は計算グラフの記事を見てもらうとして、やっていること自体は前述の偏微分の処理を「より効率的に」行っているに過ぎません。
いったん、順方向に計算を行い(学習、推論と同様の計算)、その結果から損失関数によって精度の悪さを計算します。
今度は、損失関数によって得られた精度の悪さを入力として「逆順」にデータを流してやることで、効率的に「微分」を行っていきます。
要は、通常の数値計算ではひたすらに非効率だったものを、この「誤差逆伝播法」を用いて効率的に微分を行おう、というのが主な目的です。
結果として、学習に必要なパラメータの補正値を効率よく計算することができるというわけなんですね。
畳み込みニューラルネットワーク(CNN)
最後に少しだけ、CNNについて触れておきたいと思います。
CNNは画像認識、音声認識などいたるところで使われています。
画像認識のコンペティションなどではほとんどがCNNベースのディープラーニングだそうです。
ちなみに「畳み込み」というのは画像処理において「フィルター」などを実装する際に用いられるものです。
このフィルターを「カーネル」と読んだりします。
画像処理の畳み込み処理については以前、Qiitaで記事に書いたのでそちらも参考にしてみてください。
CNNでは畳み込み層とプーリング層が増える
前述のニューラルネットワークではいくつかのレイヤ(層)を形成して、すべてのレイヤを経由してなにがしかの値を出力する、という作りになっていました。
しかし、CNNではそこに「畳み込み層」と「プーリング層」のふたつが追加されます。
なお、畳み込み層のフィルター(カーネル)が「重み」に該当します。
畳み込み層の役割
前述のニューラルネットワークではすべての層のすべてのノードが、前後の層のノードとすべて結合していました(全結合層)。
そしてその計算の際、例えば2次元データである画像(チャンネル要素も含むと3次元)も1次元の配列に変換して計算を行っていました。
つまり、本来であれば3次元的に見たときに連続したデータであったとしても、1次元配列となった時点でそれらの詳細が失われてしまうことになります。
なんとなく問題が出てしまいそうなのが分かるかと思います。
そこで、畳み込みを利用することで、多次元の要素をその次元のまま扱い、隣あうデータなどからより詳細な情報を算出できるようにする、というのがCNNの特色です。(と解釈しています)
まとめ
以上でニューラルネットワーク編はおしまいです。
(だいぶ長い記事になってしまった・・・)
今回の記事ではニューラルネットワークの基礎的な部分を解説しました。
(解説というか、本を読んで自分が理解した(気になっている)部分をメモしたに過ぎませんが・・・。きっと将来、このへんの細かいところを忘れているだろうと思っているので、そのときに思い出すきっかけに、と書いたものです。まさに備忘録w)
色々な単語や概念が出てきたかと思いますが、理解するためのポイントとして大事なところは以下の2点かなと思っています。
- 物事を認識するためのニューロンの層を構築する
- 認識精度を自己学習するための「勾配降下法」を用いて最適化する
これだけです。
あとの部分はそのための手法や、最適化についての話になるかと思います。
もちろん、これを元に実際に実用性のあるものを構築しようとしたら、まだまだ足らない知識や足らない実装がたくさんあると思いますが、少なくとも昨今のディープラーニングの記事を読むときに、なんとなくは、内部でどんな事が行われているのかという雰囲気はつかめるようになったかと思います。