概要
最近のもっぱらの興味はディープラーニングです。
ディープラーニング自体の基礎から学習しようと、本記事のタイトルの本を手に取って学習を始めたのでそこで得た知識の備忘録です。
(書籍はこちら↓)
ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装
なお、本記事はこの本を読んで得た知識を備忘録としてまとめたものになります。
さらに、色々メモを取るには(自分の中で)新しい概念が多く、とても長い内容になってしまうのでまずは「パーセプトロン編」ということで、ニューラルネットワーク・ディープラーニングの元となっている考え方についてフォーカスを当てて記事を書いていきます。
そして当然ですが、多分に自分の理解を交えた記事になっています。
なので認識を間違えているところなどがあることを先に断っておきます。
しっかりとした内容を学ぶためには上記の本を読んでみてください。
上記の本では、算術ライブラリなどを除く基本的なライブラリ以外はまったく使用せずディープラーニングを構築していきます。
だからこその「ゼロから作る」なのです。
そのため、だいぶディープラーニングについての下準備ができました。
とても良書なのでぜひ手にとってみてください。
この記事で少しでもその内容を感じ取ってもらえたらと思います。
余談ですが、UnityにもML Agentというディープラーニングを用いたプラグインがあります。
このプラグインはGoogleが提供している「TensorFlow」というフレームワークを利用したものです。
(なので学習にはPythonを利用します)
ちなみにUnity ML Agentを解説してくれている書籍もあり、とても分かりやすいのでオススメです。
Unityではじめる機械学習・強化学習 Unity ML-Agents実践ゲームプログラミング
この本では、Unity上でどうやって学習させていくかを丁寧に解説してくれています。
また、ML Agentに同梱されているサンプルも分かりやすく解説してくれています。
しかしながら、やはり中でなにが行われているのか、ブラックボックスな部分が大きいと気持ち悪さがあります。
なにかあったときに当たりがつけづらくなりますし、柔軟性のある対応ができません。
なので本記事の対象である書籍が、このブラックボックスに対しての答えになってくれると思っています。
ディープラーニングとは
そもそもディープラーニングとはなんでしょうか。
Wikipediaから引用させてもらうと、
ディープラーニングまたは深層学習(しんそうがくしゅう、英: deep learning)とは、(狭義には4層以上[1][注釈 1]の)多層のニューラルネットワーク(ディープニューラルネットワーク、英: deep neural network)による機械学習手法である[2]。深層学習登場以前、4層以上の深層ニューラルネットは、局所最適解や勾配消失などの技術的な問題によって十分学習させられず、性能も芳しくなかった。しかし、近年、ヒントンらによる多層ニューラルネットワークの学習の研究や、学習に必要な計算機の能力向上、および、Webの発達による訓練データ調達の容易化によって、十分学習させられるようになった。その結果、音声・画像・自然言語を対象とする問題に対し、他の手法を圧倒する高い性能を示し[3]、2010年代に普及した[4]。
ということ。
いきなりだとなんのこっちゃ、ですが、人間がニューロンによって情報伝達を行い、情報処理をしていることをプログラム的に模倣したもの、と考えるといいかと思います。
人間のニューロンの仕組みを模倣している?
上でも書いたように、ニューラルネットワークを学んでいくとまさに人間の脳のモデル化だなと思う部分があります。
実際、ニューラルネットワークについてWikipediaから引用させてもらうと以下のように記載されています。
ニューラルネットワークはシナプスの結合によりネットワークを形成した人工ニューロン(ノード)が、学習によってシナプスの結合強度を変化させ、問題解決能力を持つようなモデル全般を指す。狭義には誤差逆伝播法を用いた多層パーセプトロンを指す場合もあるが、これは誤った用法である。一般的なニューラルネットワークでの人工ニューロンは生体のニューロンの動作を極めて簡易化したものを利用する。
まだまだ人間の脳と同一と呼ぶことはできないですが、「簡易化した人間の脳のモデル」というのはとてもワクワクしますね。
さて、このニューロンに近い考え方、実装の仕方をしたものに「パーセプトロン」と呼ばれるものがあるそうです。
パーセプトロン
まずはニューラルネットワークのベースの考え方となっているパーセプトロンの説明から。
これまたWikipediaから引用させてもらうと、
パーセプトロン(英: Perceptron)は、人工ニューロンやニューラルネットワークの一種である。心理学者・計算機科学者のフランク・ローゼンブラットが1957年に考案し、1958年に論文[1]を発表した。モデルは同じく1958年に発表されたロジスティック回帰と等価である。
パーセプトロンはニューラルネットワークのベースになっている概念で、ひとつのパーセプトロンによって(プログラムで言うところの)ANDやORなどの回路を設計することができるようです。
つまり、入力に対してひとつの出力を得ることができる、ということです。
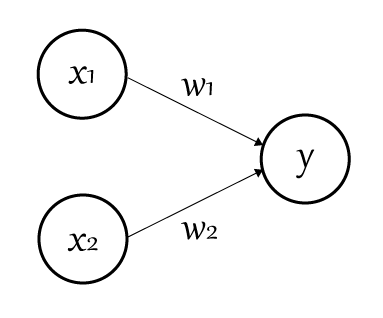
パーセプトロンは以下の図のようにあらわされます。
○はニューロンやノードと呼ばれます。そして$x_1$と$x_2$が入力信号を表し、$w_1$と$w_2$の「重み」を乗算しそれを合算したものを出力します。
そしてここで、「ある閾値」を超えた場合に電気信号は「1」を、そうでない場合は「0」を出力します。
これを「ニューロンの発火」などと呼ぶこともあります。
閾値を「$\theta$」と置くことにして数式にしてみると以下のようになります。
\begin{eqnarray}
y {=}
\begin{cases}
0 & : (w_1 x_1 + w_2 x_2) \leq \theta \\\
1 & : (w_1 x_1 + w_2 x_2) > \theta
\end{cases}
\end{eqnarray}
入力信号に対して重みを合算した結果の評価により分岐するのが分かるかと思います。
さらにこれを一般化しておくと以下のようになります。
\begin{eqnarray}
y {=}
\begin{cases}
0 & : (b + w_1 x_1 + w_2 x_2) \leq 0 \\\
1 & : (b + w_1 x_1 + w_2 x_2) > 0
\end{cases}
\end{eqnarray}
上の式の「$\theta$」を「$-b$」として右辺を0にしたものです。
そしてこの「$b$」を「バイアス」と呼びます。
上の式を見てもらうと分かりますが、このバイアスの値によって「ニューロンの発火のしやすさ」が変化することになります。
パーセプトロンでOR回路
上記の式を用いて試しにOR回路を作ってみましょう。すると以下のような式として表すことができます。
\begin{eqnarray}
y {=}
\begin{cases}
0 & : (-0.5 + x_1 + x_2) \leq \theta \\\
1 & : (-0.5 + x_1 + x_2) > \theta
\end{cases}
\end{eqnarray}
ちなみにここでは「$b = -0.5$」、「$w_1 = w_2 = 1$」です。
OR回路なので$x_1$と$x_2$に入るのは「$0$か$1$」です。
$x_1$と$x_2$に0と1を色々入れてみると、確かに$x_1$と$x_2$のどちらか(あるいは両方)に$1$が入るときに0以上の値になることが確認できると思います。
重み、バイアスは人間の手で設定する必要がある
上で示したOR回路は、バイアスと重みがそれぞれ「$-0.5$」と「$1$」でした。
これは「人間が」そう設定したわけですね。(人間が、どういうパラメータならOR回路になるか、を考えて設定したということです)
しかしこれでは機械「学習」とは言えません。
今回の記事では触れませんが、次回に書く予定の「ニューラルネットワーク」ではこのあたりの学習についても触れていきます。
パーセプトロンではバイアス、重みの値は人間がする必要がある、ということだけ覚えておいてください。
パーセプトロンの限界
ひとつのパーセプトロンだけでは限界があり、ひとつのパーセプトロンでは「線形」で表される回路しか作ることができません。
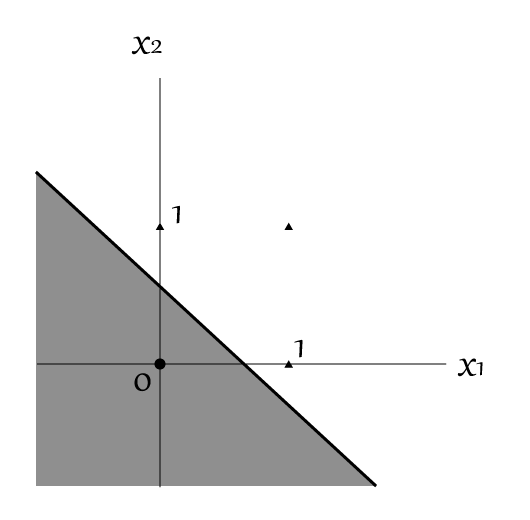
例えば、上のOR回路を図にしてみると以下の図のようになります。
●と▲を分離する線がパーセプトロンによる出力結果になります。
$x_1$と$x_2$の線上に乗っている▲がパーセプトロンへの入力「1」を表しています。
図では、直線によって●と▲が区切られているのが確認できますね。(網掛け部分が「0」を、それ以外の領域が「1」を出力します)
つまり、しっかりと式で書かれていたことが示されているわけです。
XOR回路は線形で表せない
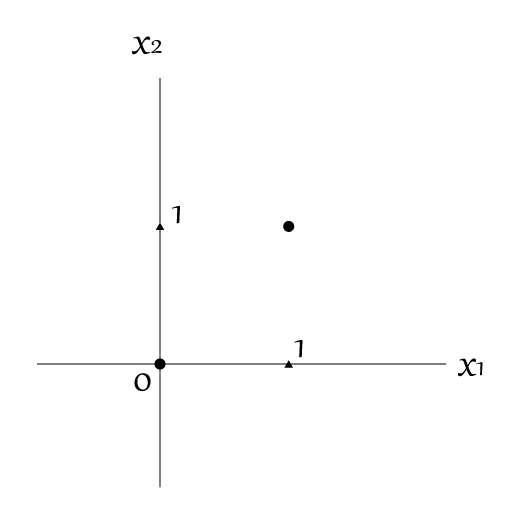
ではXOR回路を考えてみましょう。
XOR回路は$x_1$と$x_2$の「どちらか片方が$1$の場合にのみ$1$」となり、両方が$1$の場合は$0$を出力するものです。
これを上の図のようにマッピングしてみましょう。
さて、この▲と●を「直線」だけで分離することができるでしょうか?
想像通り、これは「直線」で区切ることはできません。
しかし「曲線」ならばこれを分離することが可能となります。
そしてこうした「複雑な処理」については、パーセプトロンを「多層」にすることで解決することができるようになります。
回路を複数つないでXORを実現する
先に答えを書いてしまうと、XOR回路は「AND」回路と「NAND」回路、「OR」回路を組み合わせることで実現することができます。
(※ NANDはANDの逆で、両方$1$の場合にのみ$0$を出力する回路)
そしてこの、「回路を複数接続する」というのが「層を複数つなぐ」ということとイコールとなります。
そしてニューラルネットワークへ
そしてこれをさらに多層に組み合わせ、より「深い」層を形成することで、本題である「ディープ(深い)ラーニング(学習)」が可能になる、というわけです。
つまり、誤解を恐れずに書けば、パーセプトロンを多層構造にして学習できる内容を大幅に拡張したものがディープラーニング、というわけです。
(注:あくまで「イメージ」です。なにかの文献や学術的な説明ではなく、自分のイメージを文章化したものだと思ってください)
ただ残念なことにパーセプトロンでは、(前述のように)「重みとバイアス」の調整を人間が行う必要があります。
この点が、昨今のディープラーニングの点と異なるところです。
ディープラーニング(ニューラルネットワーク)ではこの「重みとバイアス」の調整を自動化し、まるで人間が物事を学ぶかのように内容を理解するようにネットワークを構築していきます。
次の記事ではディープラーニングの基礎となっている「ニューラルネットワーク」について書いていきたいと思います。