デバッグ力を高める！ ～5 年間の経験から学んだ、競プロ・アルゴリズム実装におけるバグ取りの戦略～

こんにちは、大学 1 年になったばかりの E869120 です。
私は 5 年前に趣味で競技プログラミングを始め、AtCoder や日本情報オリンピックなどに出場しています。ちなみに、2021 年 5 月 5 日現在、AtCoder では赤（レッドコーダー）です。

今回は、アルゴリズムや競技プログラミングの問題を速く解くために必要な、効率的なデバッグの方法について記したいと思います。是非お読みください。

1. はじめに

皆さんがプログラミングの問題を解いていく際に、次のような場面に遭遇したことはありますでしょうか。おそらく、読者の大半が「はい」と答えると思います。

ソースコードに謎のミスを埋め込んでしまったせいで D 問題が解けない…
ああ、プログラムを 1 文字変えただけで WA（不正解）が AC（正解）に変わった、悲しい…

このように、プログラムにバグ（プログラム実装上のミス）を埋め込んでしまったせいで、

• 本来解けるはずだった問題の正解が遅れる
• 最悪の場合、コンテスト時間中に解けず、ついには競技が終了してしまう

といった場合もあるのです。これは初心者から最上級者まで、灰コーダーからレッドコーダーまでの共通の悩みであり、プログラムを一切バグらせない参加者は聞いたことがありません。

「バグ取りの時間短縮」の重要性

実際、自分の書いたプログラムをバグらせること、そしてバグを直すのに時間がかかってしまうことは、競技プログラミングにおいて致命的です。ひとつ例を挙げてみましょう。例えば、日立製作所社会システム事業部プログラミングコンテスト2020 において A 問題・B 問題の 2 問を解いた参加者のパフォーマンスは、次表の通りになっています。

時間（ペナルティ）	5 分	10 分	15 分	20 分	25 分
パフォーマンス	1792	1302	1008	816	679
参加者内順位	上位 12%	上位 27%	上位 40%	上位 50%	上位 57%

そこで、プログラムをバグらせなかったら 5 分で解けたはずの参加者がいたとしましょう。仮にバグのせいで 10 分追加で必要となった場合、パフォーマンスは 1792 から 1008 まで急落します。また、AtCoder では次のような特殊ルールがあります。

1 回誤答（WA や TLE など）の提出をするごとに、5 分間のペナルティが加算される。

したがって、仮にこの参加者がバグのせいで 2 回 WA（不正解） を出したとすると、ペナルティの合計が 5 + 10 + 5 + 5 = 25 分となり、パフォーマンスは 679 まで落ちるのです。たった一つのバグによって、天国と地獄ほどの差になってしまうことがよく分かると思います。

バグには典型的な対処法がある

しかし、バグを発生させる理由には、例えば次のような「典型パターン」があります。

• 添え字（$i, j$ など）を書き間違える
• コーナーケース（$H=1, W=1$ などの特殊ケース）を見落としてしまう

したがって、いくつかの点を気を付けたり、プログラムをバグらせた時の対処法を身に付けることで、ある程度デバッグにかける時間を軽減することができるのです。

本記事の概要

そこで本記事では、

• 前半で、埋め込みやすいバグの「典型パターン」
• 後半で、バグを発生させない、あるいはバグを速く修正するための典型テクニック

について、実際にバグ取りを行ってみる実戦編を交えながら解説します。

主にデバッグに苦手意識を持つ競技プログラミング参加者を対象とした記事ですが、実務でのプログラミングでも活用できるテクニックが含まれているかもしれないと考えているので、競プロ未経験の方も是非お読みください。なお、本記事では C++ の実装例を紹介していますが、読者が使うプログラミング言語に関係なく読める内容になっているでしょう。

目次

章	タイトル	備考
1.	はじめに
2.	そもそもどんなバグが起こるのか？	ここからサポートします
3.	ステップ A｜バグのないプログラムを書く方法
4.	ステップ B｜バグを起こしたらどうすれば良いか？	本記事のメインです
5.	ステップ C｜最終手段・ランダムチェッカーのすすめ
6.	ステップ D｜それでも原因が見つからない場合
7.	おわりに
8.	参考文献・参考資料

2. そもそもどんなバグが起こるのか？ ～典型パターン 10 個を整理～

いきなり、本命の「バグを減らす方法」「デバッグのテクニック」を紹介したいところですが、

• プログラムを書くときに、どのようなバグを発生させやすいのか

が理解できていなければ、実際にテクニックを活用するのは難しいです。一方、対戦型ゲームで敵の特徴を知れば勝ちやすくなることと同じように、バグの主原因を知ればデバッグもしやすくなるのです。そこで 2 章では、「典型的なバグ」を次の 10 個のパターンに分けて記します。 なお、タイトルに記載されている「頻出度」は、星の数が多いほど起こしやすいバグであることを意味します。5 が最高ランクです。

• 1 点目：入出力の形式を間違える
• 2 点目：型（int, long long など）を間違える
• 3 点目：添字を書き間違える
• 4 点目：境界や不等号を間違える
• 5 点目：操作を 1 個書き忘れる
• 6 点目：場合分けを忘れる
• 7 点目：オーバーフローや誤差のせいで不正解となる
• 8 点目：配列外参照をする
• 9 点目：複数テストケースの問題で、初期化を忘れる
• 10 点目：そもそも解法が間違っている

2-1. 入出力の形式を間違える（頻出度：3）

AtCoder などで出題される問題では、「入力」セクションに入力順序が書かれています。

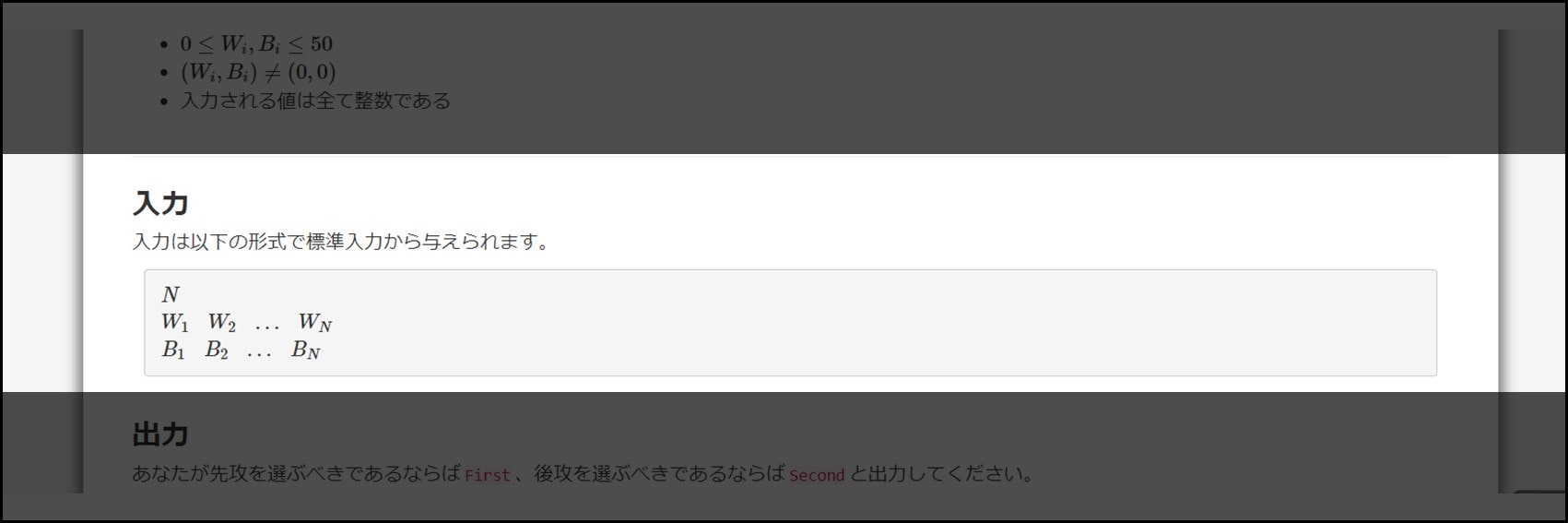
そこで、次のように間違った順序で入力を行うと、当然 WA（不正解）になってしまいます。一見当たり前のように思えるかもしれませんが、実は意外とやらかすミスです。

問題を速く解こうとするあまり入力セクションを確認し忘れ、自分の感覚に頼って「入力形式はこれだ！」と頭の中で勝手に決めつけてしまうことがあるので、注意が必要です。（私自身も過去に何度も失敗しています。）

#include <iostream>
using namespace std;
int N, W[100009], B[100009];
int main() {
    cin >> N;
    for (int i = 1; i <= N; i++) cin >> W[i] >> B[i];
    // 以下略
    return 0;
}

それに関連して、他にも次のようなミスが考えられます。

• $N$ と $K$ などの入力順を間違える（特に入力される値が 2・3 個しかない場合に注意）
• 入力が $N-1$ 行のところを $N$ 行入力してしまう（木構造が与えられる場合など）
• Yes と出力すべきところを間違って YES と出力してしまう
• 構築問題（答えの一例を出力させる問題）で、出力の順序や形式を間違える

2-2. 型（int・long long など）を間違える（頻出度：4）

まず、以下の問題を考えてみましょう。（出典：ABC165B）

高橋君は銀行に $100$ 円を預けており、毎年 $1\%$ の利子が付きます（複利、小数点以下切り捨て）。預金額が初めて $X$ 円以上になるのは何年後ですか？（制約：$101 \leq X \leq 10^{18}$）

この問題は単純なシミュレーションで解くことができますが、例えば次のようなプログラムを書くと WA（不正解）になってしまいます。

#include <iostream>
using namespace std;

int main() {
    int X, cur = 100, cnt = 0;
    cin >> X;
    while (cur < X) {
        cur += cur / 100;
        cnt += 1;
    }
    cout << cnt << endl;
    return 0;
}

理由はオーバーフローです。int 型は 32 ビット整数であるため、$X=10^{18}$ といった大きな数を表すことができないのです。それぞれの型で表せる整数の範囲は次表の通りであるため、この問題では long long 型を扱う必要があります。

型	表せる範囲（正確なもの）	大まかな値
int など、32 ビット整数	$-2^{31} \leq x < 2^{31}$	$±2×10^9$ 程度
long long など、64 ビット整数	$-2^{63} \leq x < 2^{63}$	$±9×10^{18}$ 程度

それに関連して、他にも次のようなミスが考えられます。

• 入力が小数であるにも関わらず、int などの整数型で入力を行ってしまう
• 入力が 2 文字以上の文字列であるにも関わらず、1 つの char 型で入力を行ってしまう
• $10^{19}$ を超える入力に対して long long などの整数型を使ってしまう（本当は string などの文字列型で入力しなければならない¹）

2-3. 添字を間違える（頻出度：5）

例えば、次のようなプログラムを考えてみましょう。

for (int i = 1; i <= N; i++) {
    for (int j = 1; j <= N; j++) cin >> A[i][i];
}

本来であれば A[i][j] が入力されるはずですが、A[i][i] となっています。単純なプログラムであればこの種のミスも少ないですが、プログラムが複雑になっていくにつれ、

• j であるはずのものが i になってしまう
• i であるはずのものが 1 になってしまう
• 1 であるはずのものが i になってしまう

など、添え字のミスが起こる可能性が高まるので、油断は禁物です。それに関連して、

• 特に変数の種類が増えた場合に、同じ変数を 2 回以上定義する
• + と -、あるいは ++ と -- を逆にする

といったバグも頻出なので、注意しておくようにしましょう。

2-4. 境界や不等号を間違える（頻出度：4）

まず、以下の問題を考えてみましょう。

整数 $X$ は 10 以上ですか？（制約：$1 \leq X \leq 20$）

この問題は、次のような実装で、簡単に AC（正解）を出すことができます。

#include <iostream>
using namespace std;

int main() {
    int X; cin >> X;
    if (X >= 10) cout << "Yes" << endl;
    else cout << "No" << endl;
    return 0;
}

しかし、意外と間違えやすいのが境界の処理です。例えば、次のようなプログラムを間違って書いてしまうと、WA（不正解）になってしまいます。

#include <iostream>
using namespace std;

int main() {
    int X; cin >> X;
    if (X > 10) cout << "Yes" << endl;
    else cout << "No" << endl;
    return 0;
}

詳しくは 4-3. 節で述べますが、不等号の種類・境界値の判定がしっかりできているかを確認することも重要です。

2-5. 命令を 1 個書き忘れる（頻出度：3）

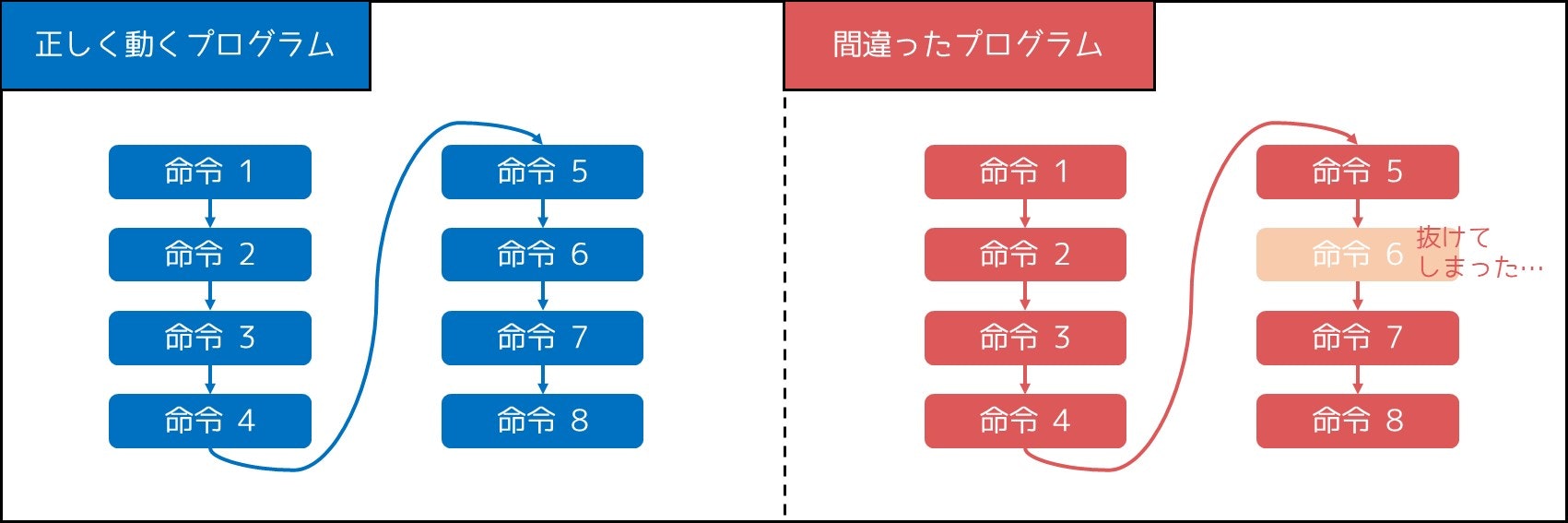
プログラミングでは、入力・出力・変数の定義・変数への加算など、様々な命令が上から順番に実行されていきますが、そのうち 1 つや 2 つが間違えて抜けた（あるいは書き忘れた）ことにより、WA（不正解）になってしまう場合もあります。

典型的なパターンとして、例えば以下のようなものが挙げられます。

• 配列や集合（C++ の場合 std::vector や std::set など）に値を追加する操作を 1 個だけ忘れる
• 無向グラフを扱う問題で $A_i \to B_i$ の辺のみを追加し $B_i \to A_i$ の辺を追加し忘れる

一見この種のバグは「ほとんどのテストケースで不正解となる」可能性が高そうに見えますが、実は大半のテストケースで正解する場合もあることに注意してください。

2-6. 場合分けを忘れる（頻出度：3）

まず、以下の問題を考えてみましょう。（出典：PANASONIC2020B）

$H \times W$ のマス目があって、一番左上のマスに角行が置かれています。角行は移動を繰り返すことで、いくつのマスに移動できますか？（制約：$1 \leq H, W \leq 10^9$）

上から $X$ 番目・左から $Y$ 番目のマスを $(X, Y)$ とするとき、$(X + Y) \bmod 2 = 0$ のマスに移動できるため、答えは $\lceil HW \div 2 \rceil$ であるように見えます。

#include <iostream>
using namespace std;

int main() {
    long long H, W;
    cin >> H >> W;
    cout << (H * W + 1LL) / 2LL << endl;
    return 0;
}

しかし、上のプログラムを提出すると WA（不正解）になります。なぜなら、$H=1$ または $W=1$ のとき、角行は一切動けず、答えが $1$ になってしまうからです。このように、特殊なケース（コーナーケース）での場合分け忘れによるバグは頻出です。

2-7. オーバーフロー・誤差によるバグ（頻出度：2）

まず、以下の問題を考えてみましょう。（出典：ABC169B）

$A_1 \times \cdots \times A_N$ が $10^{18}$ を超えるか判定してください。（制約：$N \leq 100, A_i \leq 10^9$）

そこで、次のようなプログラムを書くと、例えば $N = 3, A_1 = A_2 = A_3 = 10^8$ の場合に WA（不正解）となってしまいます。

#include <iostream>
using namespace std;

int main() {
    long long ret = 1, A[100009];
    for (int i = 1; i <= N; i++) cin >> A[i];
    for (int i = 1; i <= N; i++) {
        ret *= A[i];
        if (ret > 1000000000000000000LL) { cout << "Yes" << endl; return 0; }
    }
    cout << "No" << endl;
    return 0;
}

理由はオーバーフローです。計算途中で ret の値が $10^{24}$ になるはずですが、2-2. 節でも述べた通り long long 型ではおよそ $9 \times 10^{18}$ までの整数しか表せないため、ret が変な値になってしまうのです。

このように、計算途中でオーバーフローしないか確認することが大切です。それに関連して、次のようなバグも頻出です。

• 「1000000007 で割った余り」を求めさせる問題で、計算途中で余りを取り忘れる
• $A_1, A_2, \cdots, A_N$ の最大値を求めさせる問題で、答えが負になるテストケースもあるのに、最大値の初期値 Answer を 0 にしてしまう
• 浮動小数点数（double 型など）の誤差の影響で、間違って大小比較が行われる（PANASONIC2020Cなど）

2-8. 配列外参照をする（頻出度：3）

まず、以下の問題を考えましょう。

$A_1 + A_2 + \cdots + A_N$ の値を出力してください。（制約：$N \leq 10^5, A_i \leq 100$）

この問題は非常に簡単ですが、例えば次のようなプログラムを書くと WA（不正解）または RE（ランタイムエラー）になってしまいます。

#include <iostream>
using namespace std;

long long N, sum = 0, A[10000];

int main() {
    cin >> N;
    for (int i = 1; i <= N; i++) cin >> A[i];
    for (int i = 1; i <= N; i++) sum += A[i];
    cout << sum << endl;
    return 0;
}

$N = 10^5$ の最大ケースを考えてみましょう。このとき、入力の時点で要素 A[100000] にアクセスしていますが、配列は A[0], A[1], ..., A[9999] までしか定義されていないため、変な挙動を起こす可能性があります。このようなミスを配列外参照といいます。

このように、配列の大きさが本当に適切であるのか、チェックすることが大切です。

2-9. 初期化を忘れる（頻出度：2）

AtCoder では、以下のような「複数のテストケースからなる問題」が出題されることがあります。（出典：AGC051F、他にも ARC116A・ARC112A などが複数テストケース形式）

$Q$ 個のテストケースが与えられます。
$i$ 個目のテストケースでは、整数 $x_i, y_i$ が与えられるので、$1$ 秒の砂時計と $\sqrt{2}$ 秒の砂時計を使うことで $x_i + y_i \sqrt{2}$ 秒が測定できるか答えてください。

このような問題では、「問題を解く際に使う変数」を 2 回以上利用する場合があります。しかし、2 個目以降のテストケースについて解く前に、変数の値を全部 0 や false にするなどの初期化処理を行わなければ、

前のテストケースの計算結果が後のテストケースの計算結果に影響を及ぼす

場合があるのです。そこで次のように、テストケースごとに初期化を行うと、正解を出すことができます。（ここでは init が初期化のために用意された関数です）²

#include <iostream>
using namespace std;
bool used[100009];
int N, A[100009];

void init() {
    // ここで初期化を行う
    N = 0;
    for (int i = 0; i < 100009; i++) used[i] = false;
    for (int i = 0; i < 100009; i++) A[i] = 0;
}
void solve() {
    // ここで問題を解く
    // 省略
}
int main() {
    int Q; cin >> Q;
    for (int i = 1; i <= Q; i++) {
        init();
        solve();
    }
    return 0;
}

2-10. そもそも解法が間違っている（頻出度：5）

本章の最後に、最大の WA（不正解）になってしまう原因を紹介します。これは、

• そもそも自分の解法が間違っている

というパターンです。以下の問題を考えてみましょう。³

$N$ 個の商品があり、$i$ 個目の商品は価値が $v_i$、値段が $w_i$ 円です。各商品は $1$ 個までしか買うことができません。値段の合計が $LIMIT$ 円以下になるように買い物を行うとき、得られる価値の合計の最大値はいくつでしょうか？

直感的には、次のような貪欲法アルゴリズムで最適解が出せると思うかもしれません。

効率 $v_i \div w_i$ が大きい順に商品を取っていく。

プログラムの実装例は、次のようになります。

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

int N, LIMIT, V[1009], W[1009];
vector<pair<double, int>> vec;

int main() {
    cin >> N >> LIMIT;
    for (int i = 1; i <= N; i++) cin >> V[i] >> W[i];
    for (int i = 1; i <= N; i++) vec.push_back(make_pair(1.0 * V[i] / W[i], i));
    sort(vec.begin(), vec.end());

    int sum_weight = 0, sum_value = 0;
    for (int i = (int)vec.size() - 1; i >= 0; i--) {
        if (sum_weight + W[vec[i].second] > LIMIT) continue;
        sum_weight += W[vec[i].second];
        sum_value += V[vec[i].second];
    }
    cout << sum_value << endl;
    return 0;
}

しかし、これは例えば $N = 3, LIMIT = 10, (v_i, w_i) = (7, 8), (5, 6), (3, 4)$ などのケースで WA（不正解）になってしまいます。実際、

• 最適解は 2 番目と 3 番目の商品を選ぶこと（価値の合計は 5 + 3 = 8）

ですが、上のプログラムでは 1 番目の商品のみを選ぶため、価値の合計が 7 となるのです。⁴

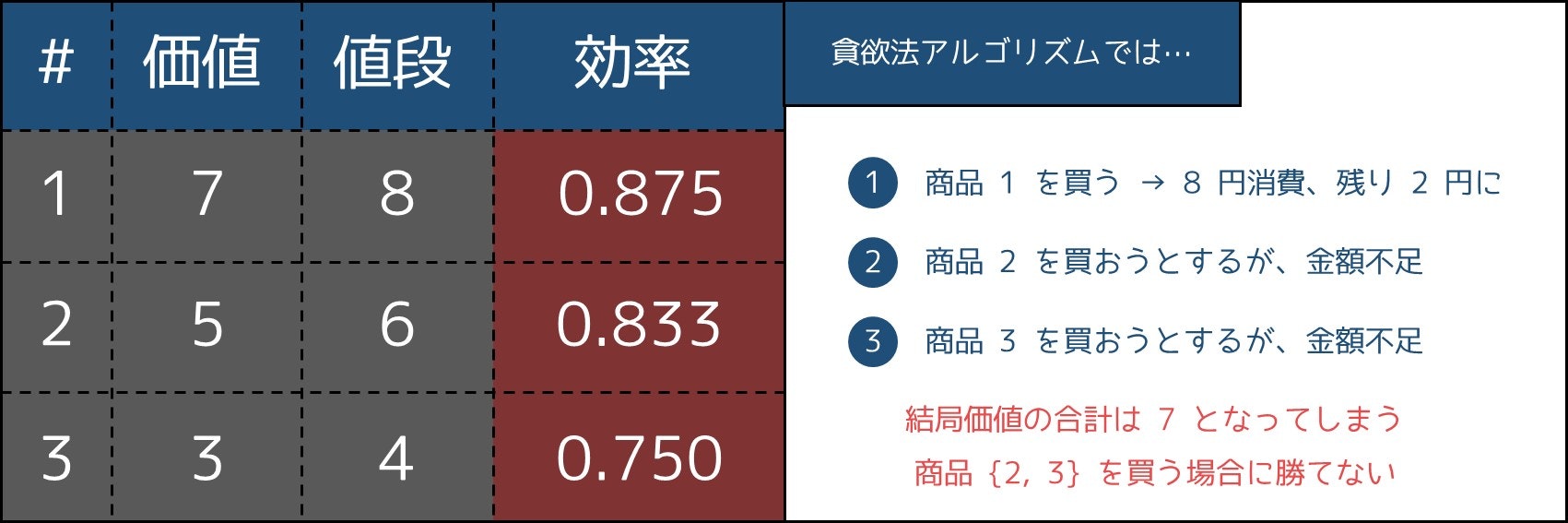
このように、「そもそも解法から間違っていること」も、不正解の原因の 1 つです⁵。詳しくは 3 章でも述べますが、これを回避する手段としては、例えば次のものが挙げられます。

• 数学的に証明してからアルゴリズムを実装する
• 全探索や動的計画法など、他の手段を検討する

---

ここまで、不正解（WA）を出す主な原因について、10 個のポイントに分けて解説しました。しかし、原因が分かっても、デバッグにかける時間を減らさなければ意味がありません。そこで 3 章では、バグの発生や不正解を出す可能性を減らす方法について記したいと思います。引き続きお読みいただけると嬉しいです。

3. ステップ A｜バグのないプログラムを書く方法

プログラミングコンテストにおいて、より速く正解を出すためには、「プログラムにバグを埋め込まないこと」が重要です。もちろんバグを発生させたときの対処も重要ですが、やはり最初に気にすべきことは「バグを減らすこと」だと思います。そこで、本章では考察や実装の観点で、デバッグをする羽目になる確率を少しでも減らす方法について、主に以下の 5 つのポイントに分けて解説したいと思います。

• 1 点目：コーディングしやすいエディタを用意する
• 2 点目：紙に実装方針を書いておく
• 3 点目：プログラムをいくつかのセクションに分ける
• 4 点目：関数を利用してコードを読みやすくする
• 5 点目：証明をきちんと考えてからプログラムを実装する

3-1. コーディングしやすいエディタを用意する

まず、皆さんに質問があります。

「メモ帳」を使って競技プログラミングの問題を解けますか？
たとえば ABC194B - Job Assignment を解いて、一発で正解を出せますか？

おそらく多くの人が自信を持って「Yes」と答えると思います。しかし、一度やってみてください。読者のうち半分程度は AC（正解）どころか、コンパイルすら通らないと思います。

コードの見やすさの面でも重要

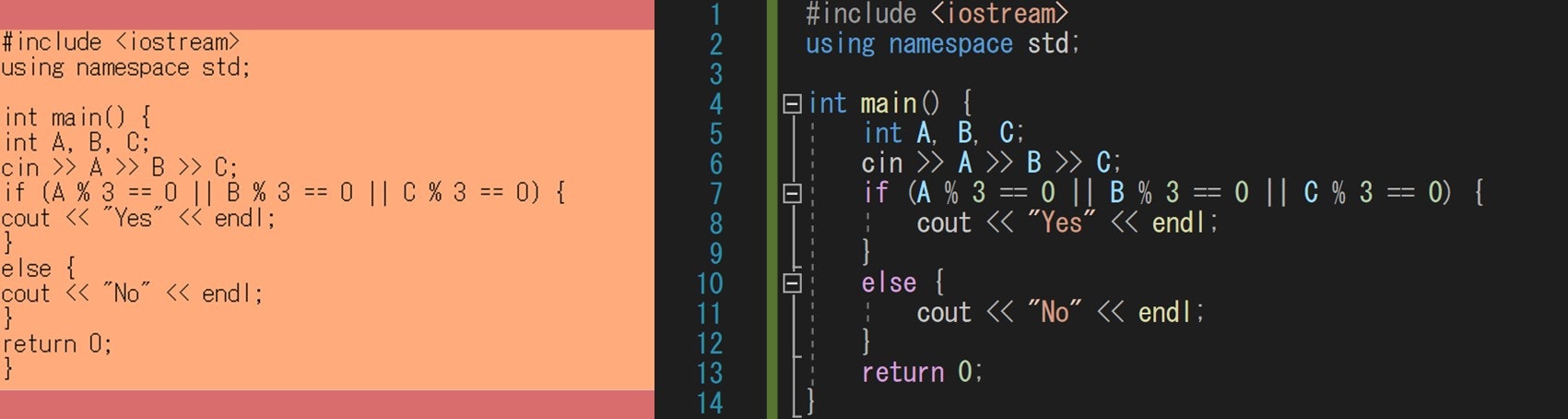
また、次の 2 つのプログラムは、どちらの方が見やすいと思いますか？

おそらく大半の人は「右の方が読みやすい」と思うはずです。当然、見やすいプログラムの方が実装やデバッグがしやすいので、このような面でも、

• 適切なインデントが自動で付けられる
• 適切なシンタックスハイライトが自動で付けられる

といった機能を備えた統合開発環境（IDE）やエディタを使うことは、競技プログラミングにおいて重要です。

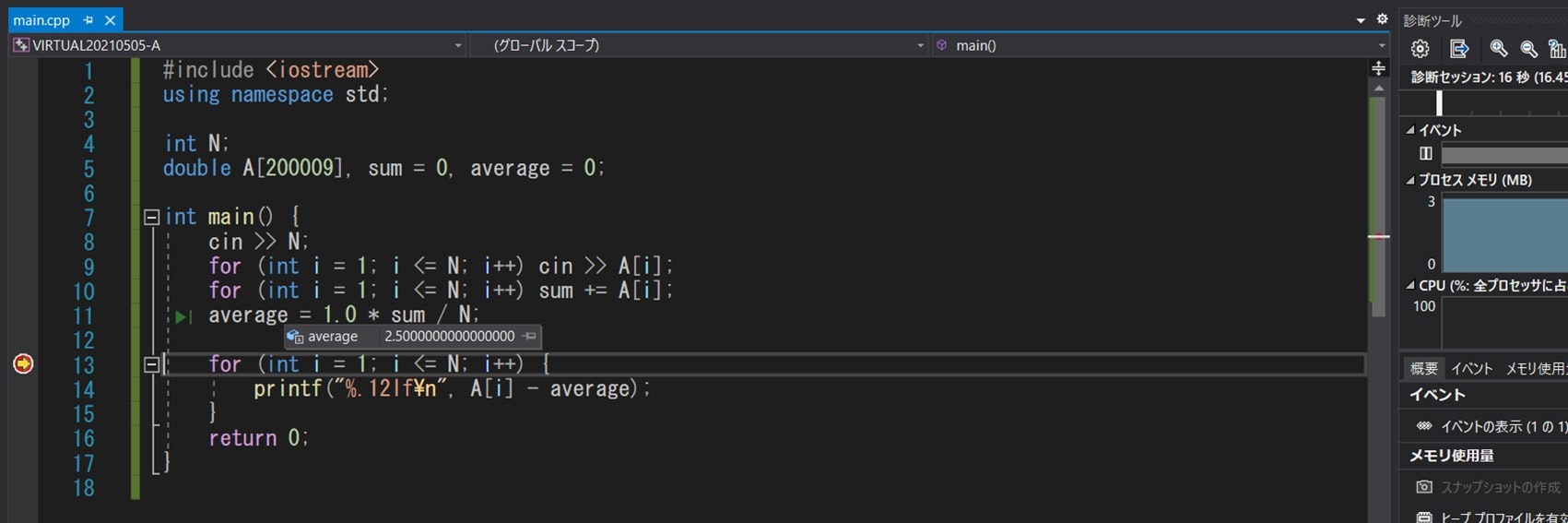
Visual Studio のすすめ

そこで私は、Microsoft Visual Studio などをお勧めしています。理由としては、次の 2 点が挙げられます。

• インデントやシンタックスハイライトが自動で付けられる
• ブレークポイント（デバッグの際に、指定箇所でプログラムを一時停止し、変数の値などを確認することができるもの）を設定することができる

一方、日本の競技プログラミング界の権威である @rng_58 さんが「Visual Studio は使いにくい」と主張しているように、人それぞれ意見が異なる点があります。したがって、自分に合った統合開発環境やエディタを選び、それに慣れることが一番重要です。

3-2. 紙に実装方針を書いておく

プログラミングコンテストで出題される問題の中には、

• 複雑な処理が要求される問題
• 多くの実装ステップが要求される問題

もあります。このような問題では、紙やホワイトボード、NotePad などに実装方針（どのようなステップでコードを書くかの概略）を書いておくことが重要です。

また、2-6. 節で述べたように、AtCoder では場合分けが要求される問題も出題されます。このような問題に対しても、

• 場合分けも含めた実装方針を紙に書く

ことで、バグを起こす可能性を軽減することができます。

[実装方針の書き方の例｜ARC117-C の場合]
1. 入力
2. N! が 3 で何回割り切れるかを配列 f[i] にメモする
3. 二項係数 C(n, r) を 3 で割った余りを計算する関数を作る
4. 答えを求める
5. 出力
※考察メモのイメージなので、理解できなくても先に進んで構いません

3-3. プログラムをいくつかのセクションに分ける

皆さん、プログラムの実装やデバッグを行う際に、次のような経験をしたことがありますか。

デバッグをするときに、どこでどういう処理を行っているか分からなくなる
そもそもどこでプログラムのミスを埋め込んだかを見つけにくい

そこで、コメントを付けてプログラムを複数のセクションに分けることで、このような問題を軽減することができます。より具体的に説明すると、

• 計算結果が正しいかどうかを、セクションごとに確認しやすい
• 実装が間違っているセクションが特定できた後も、バグを見つけやすい（20 行のセクションと 100 行のセクションでは、当然前者の方がデバッグが速い）

といったメリットがあります。しかし、あまりにもコメントが多すぎると逆に見にくくなってしまうので、10 ～ 30 行につき 1 個の割合で分割することを推奨しています。（例えば、下の実装は少しセクション数が多すぎるかもしれません）

#include <iostream>
#include <algorithm>
using namespace std;

long long N, A[1 << 18];

int main() {
    // Step #1. 入力
    cin >> N;
    for (int i = 1; i <= N; i++) cin >> A[i];

    // Step #2. 答えの計算
    long long Answer = 1, mod = 1000000007;
    sort(A + 1, A + N + 1);
    for (int i = 1; i <= N; i++) {
        Answer *= (A[i] - A[i - 1] + 1);
        Answer %= mod;
    }

    // Step #3. 出力
    cout << Answer << endl;
    return 0;
}

3-4. 関数を利用してコードを読みやすくする

皆さん、プログラムの実装において、このような経験をしたことがありますか。

プログラムが 5 重ループを含んでしまい、実装が大変になってしまった…
ほとんど同じ処理をいろいろな箇所に 3 回書いてしまい、コードが長くなってしまった…

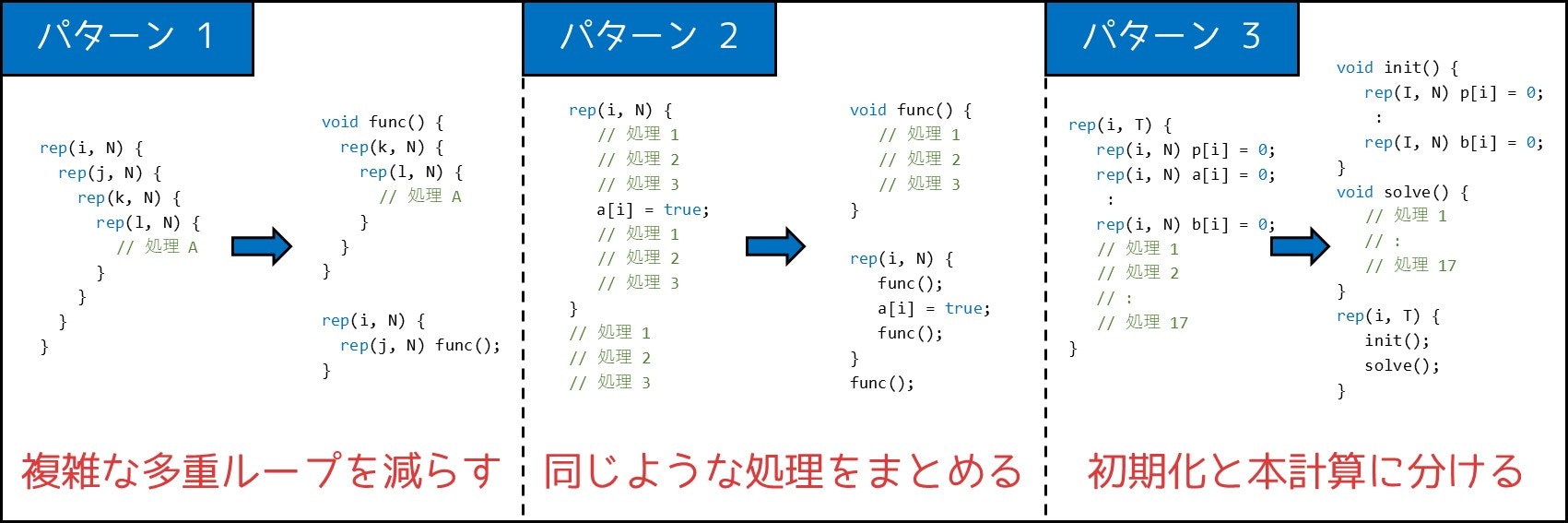
そこで、関数を使うことで実装量が減ったり、プログラムが読みやすくなったりする場合があります。具体的に述べると、関数を使うべき（と個人的に思っている）場面は、主に 3 つのパターンに分けられます。

• 4 重以上の多重ループをなんとかして分割したいとき
• プログラム中に、同じような処理を 2 度・3 度書いているとき
• 複数テストケースの問題で、初期化を行いたいとき（2-9. 節参照）

イメージとしては、下図のような感じです。（注：ここでの rep(i, N) は、for (int i = 1; i <= N; i++) を意味します。rep マクロとも呼ばれる書き方です。）

3-5. 証明を考えてからプログラムを実装する

2-10. 節でも述べたように、不正解（WA）を出してしまう最大の原因は「そもそも解法が間違っていること」、つまり嘘解法を生やしてしまうことです。実際に、

この解法はなんか正しそうだ、実装してみよう！

と思っても、実は解法が間違っていたというケースはたくさん聞きます。したがって、特に貪欲法（Greedy）など誤った直感に走りやすいアルゴリズムを扱う場合、「WA を出したとき解法が間違っている可能性を常に念頭に置くこと」は重要です。

なお、解法自体のミスを減らす方法はたくさんあります。例えば、

• 数学的に証明を考えてから実装する
• 紙の上でいくつかのテストケースを試してから実装する
• 全探索や動的計画法など、比較的確実性の高いアルゴリズムを使う

などが挙げられます。⁶

---

ここまで、バグや原因不明の不正解（WA）を発生させない方法について、5 つのポイントに整理して解説しました。しかし、それでもプログラマーは人間なので、確実にバグらせないことは不可能です。では、バグを起こしてしまった場合、どのように対処すれば良いのでしょうか。4 章ではこれについて記したいと思います。

4. ステップ B｜バグを発生させたらどうすれば良いか？

3 章でも述べたように、プログラムを実装していく過程でバグを埋め込まないことは大切です。しかし、ときどきバグを発生させることがあるのは、プログラミング初心者からレッドコーダーまで、人類共通の悩みです。

では、どうやってバグの解消、つまり「デバッグ」を行うことができるのでしょうか。これは大きく分けて 2 つのステップからなります。デバッグでは、それぞれのステップを効率的に行うことが重要です。

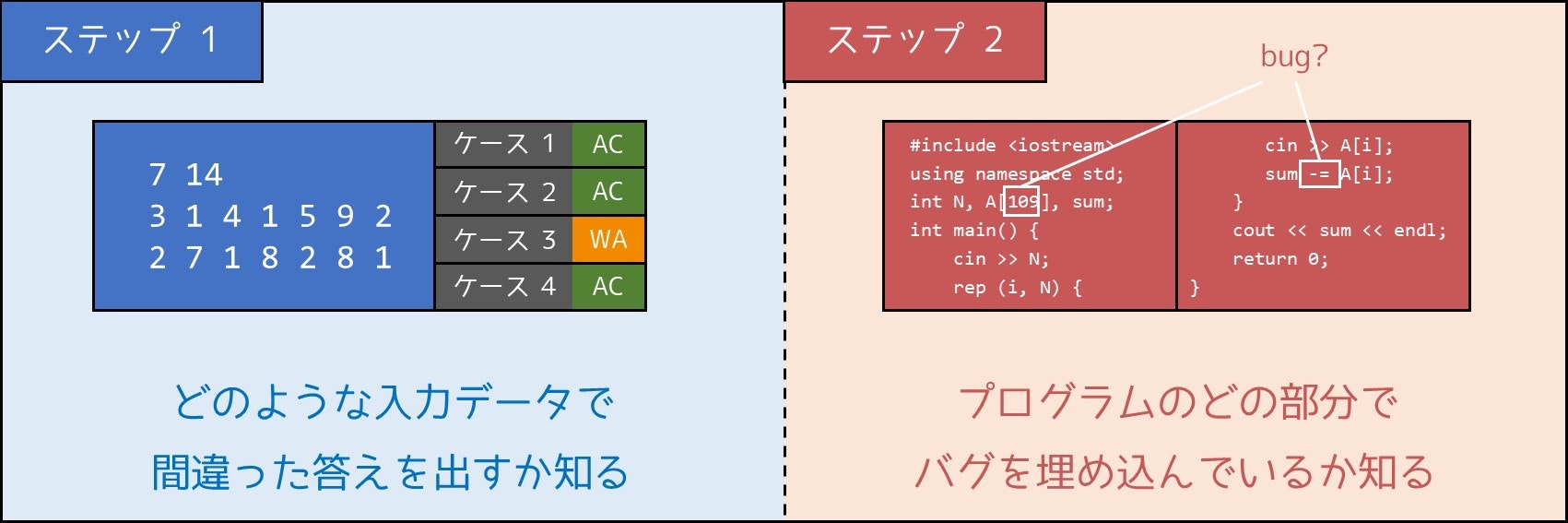
そこで本章では、デバッグの方法を 5 つのポイントに分けて解説したいと思います。実際に、次の手順に従ってデバッグをすると、経験的に上手くいくことが多いです。

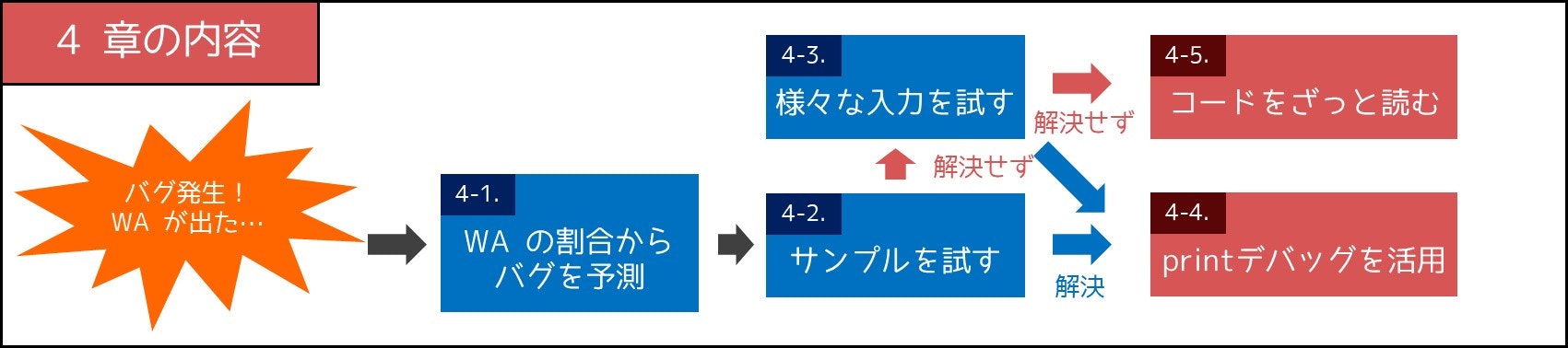
4-1. WA の割合からバグを予測（重要度：5）

あなたがプログラミングコンテストの問題で提出を行うも、残念ながら WA（不正解）が出てしまったとします。そこで、最初に行うべきことは何でしょう。これは、

どの程度のテストケースで WA（不正解）となっているか確認する

ことです！！！

WA の個数はどこで確認できるか？

AtCoder などのコンテストサイトでは、「提出詳細」のリンクに飛ぶと、次のような表示を見ることができます。これはコンテスト中・コンテスト終了後問わず閲覧可能です。

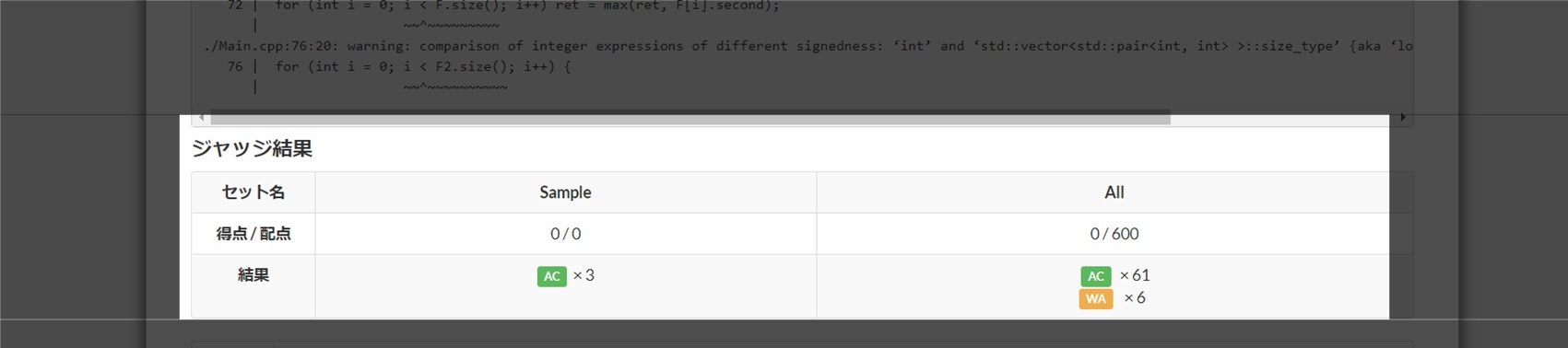
ここでは、主に以下の 3 点を確認することができます。

• サンプルケース（入出力例）では正解しているか？
• どのような原因で不正解となっているか？（WA・TLE・RE など）
• どの程度の割合のテストケースで不正解となっているか？

例えば上図の場合、サンプルケースでは全部正解している一方、全体では約 1 割のテストケースで不正解となっており、原因は WA であることが分かります。

---

そこで、それぞれの原因に対してどのようなバグや対処法が考えられるのでしょうか。全部で 5 つのパターンに大別できます。

パターン A｜サンプルに不正解がある

問題文中に提示されている入出力例のうち 1 つ以上で間違った出力をしています。
4-2. 節に書かれている通り、入出力例を確認しましょう。

パターン B｜原因が RE の場合

配列外参照や 0 割り（11 / 0・24 % 0 など、0 で割る計算を行う）などの理由が考えられます。コードをざっと読むとき、この種のバグを中心に確認すると良いです。（なお、配列外参照は必ずしも RE とは限らず、WA と表示される場合があることに注意してください）

パターン C｜原因が TLE の場合

そもそもアルゴリズムの効率が悪いケースの他にも、for 文や while 文の処理をバグらせてしまい、無限ループに陥っている可能性もあります。

パターン D｜原因が WA で、1～5 割程度しか正解がない場合

プログラムの根本的な部分で間違っている可能性が高いです。このような場合、4-3. 節に書かれている通り、サンプル以外のいくつかの入力データについて調べることで、誤答となるテストケースを探し出す手法が有効です。

パターン E｜原因が WA で、8～9 割程度正解がある場合

場合分けを忘れていたり、コーナーケースで引っかかっている可能性もあるので、このような点を確認すると良いです。しかし、軽微なバグや想定嘘解法の影響で、偶然このパターンになるケースもあるため、一概には言えません。⁷

---

このように、不正解の原因や個数を参考にすることで、バグの原因が絞り込める場合があります。しかし、「このようなバグの可能性が高い」だけであって、確実にそうとは限らないのでご注意ください。

4-2. サンプルを確認しよう（重要度：4）

AtCoder などプログラミングコンテストの問題文には、いくつか入出力例が付いています。通常は、3 個程度のテストケースが掲載されている場合が多いです。

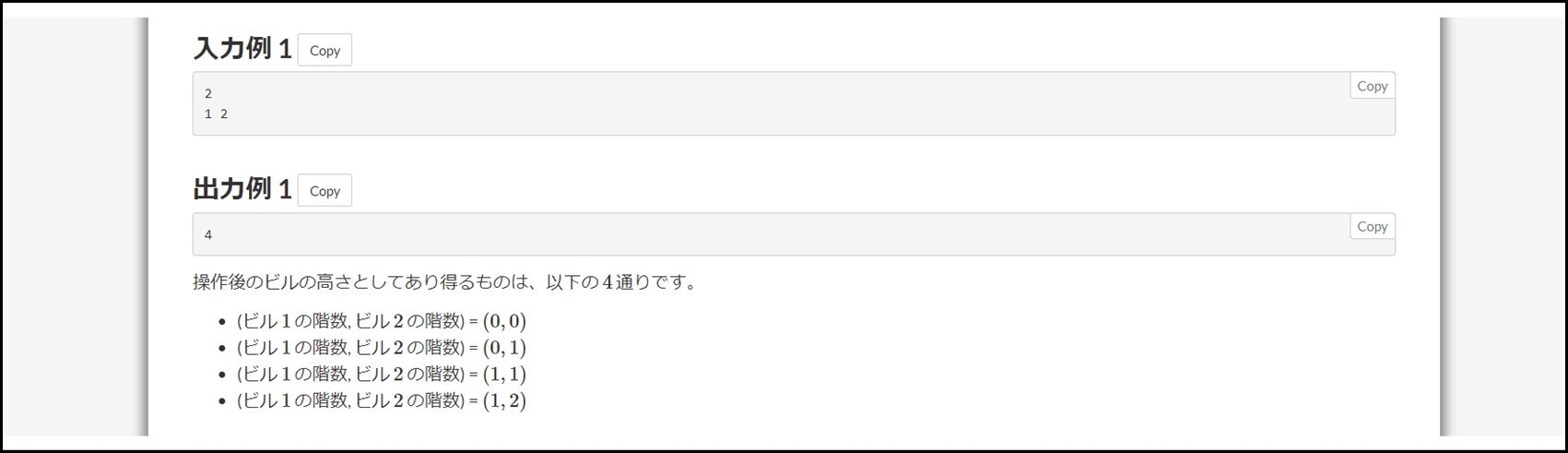
もしジャッジ結果の「Sample」セクションに不正解の表示があった場合、すぐに入出力例を全部試してみましょう。高々数個なので、1 分以内で「どのテストケースで誤答を出すか」確認できると思います。

そもそも提出の前に入出力例を試すべき

しかし、1 回の誤答につき 5 分間のペナルティが付くことを考慮すると、せっかく一部のテストケースが公開されているにも関わらず、それを使わないのは大損です⁸。ですが、残念ながら WA の提出のうち約 46% がサンプルケースのうち 1 個以上で不正解を出しているという衝撃の事実があり、意外と見落としやすい点でもあります⁹。

環境構築ができていない人は？

もしかしたら、人によっては Visual Studio のようなテスト環境を持っていない影響で、入出力例のチェックを行っていないかもしれません。しかし、AtCoder には自動でプログラムを実行する、コードテストという超便利機能があります。それを活用すると、環境が無くても WA の数を大幅に減らすことができるのです。（それに関連して、AtCoder Easy Test という、入出力例を自動で試してくれるソフトもあるので、これも是非利用してみましょう）

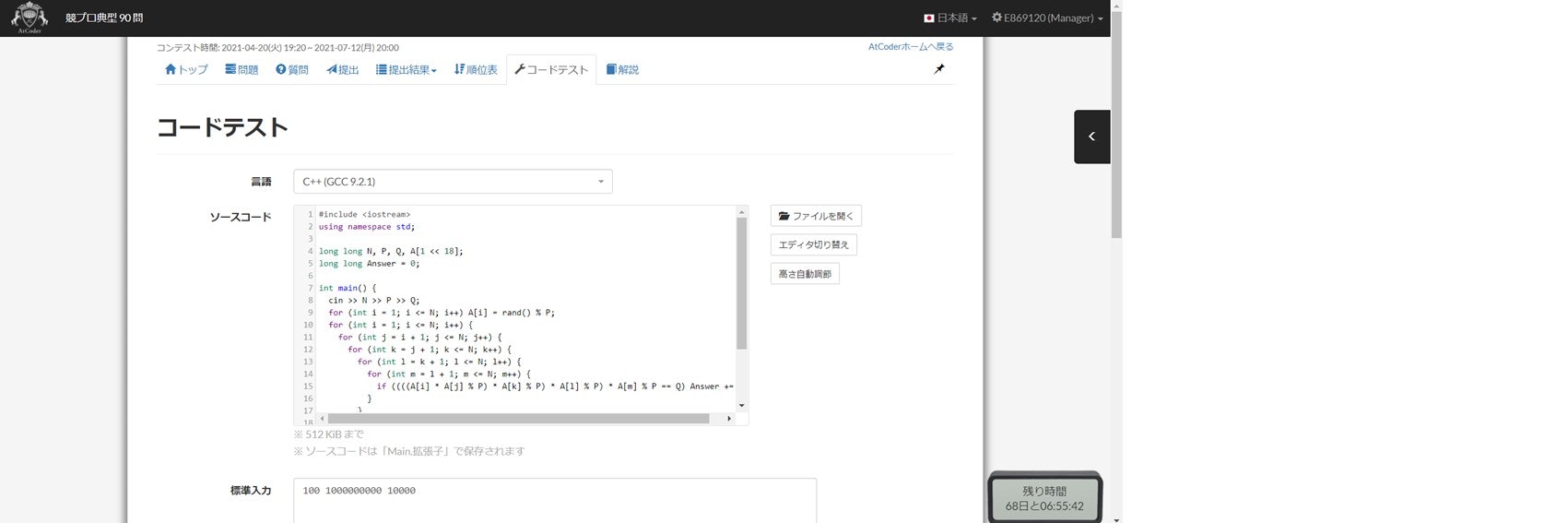
4-3. 適当なテストケースで試す（重要度：4）

4-2. 節では入出力例でのテストについて紹介しましたが、

サンプルでは全部正解したのに、その他のテストケースで合わない…

といった場合、どうすれば良いのでしょうか。1 つの対処法として、「適当なテストケースをいくつか入力して、合っているか調べる」ことが考えられます。サンプルケースは概ね 3 個程度と多くないため、追加で 10 個程度の「入力サイズが小さいテストケース」を自分で作って試すことで、誤答を出す入力データが 1 つ見つかる場合があります。

それに関連して、次のようなコーナーケースを試すことも重要です。これらは問題作成者側の意図で、あえて入出力例に載せない場合もあるため、追加で試す必要が出てきます。

• $N = 1, H = 1$ のような、入力される値が非常に小さい場合
• $A_1 = A_2 = \cdots = A_N$ のような特殊ケース
• 条件ギリギリの境界値をとるようなケース
• $N$ は小さいが $A_1, A_2, \cdots, A_N$ が大きいような、オーバーフローを誘発するケース

基本的に、入出力例を全部チェックするだけでも WA を出す可能性が大幅に減るので、誤答の確率を少しでも減らすために「提出する前に追加で 10 ～ 20 個のテストケースを試す」という戦略に出ることは時間の無駄であり、良い立ち回りではありません。しかし、一度 WA が出たら、このテクニックが有効になると思います。

4-4. print デバッグをする（重要度：2）

では、4-2. 節または 4-3. 節で紹介した方法で、誤答を出すテストケースが 1 つ判明したとしましょう。この先、どのようにして「プログラムの間違いがある箇所」を特定すれば良いのでしょうか。1 つのアイデアとして、次のものが挙げられます。

プログラムの途中の時点で、計算結果がおかしくなっているか調べる。

より分かりやすく説明するため、例を紹介します。以下のプログラムを考えてみましょう。

#include <iostream>
using namespace std;

int N, A[100009], B[100009];
int Q, L[100009], R[100009];

int main() {
    cin >> N;
    for (int i = 1; i <= N; i++) cin >> A[i];
    for (int i = 1; i <= N; i++) B[i] = B[i - 1] + A[i];
    // cout << B[N] << endl;
    cin >> Q;
    for (int i = 1; i <= Q; i++) {
        cin >> L[i] >> R[i];
        cout << B[R[i]] - B[L[i] - 1] << endl;
    }
    return 0;
}

そこで、例えば次のようなケースでバグを発生させたとしましょう。A[L] + A[L + 1] + ... + A[R] を出力させる意図のプログラムであるため、本来ならば 3000000000 を出力させるはずなのですが、残念ながら -1294967296 という出力を行っています。

3
1000000000 1000000000 1000000000
1
1 3

そこで、cout << B[N] << endl のコメントアウトを外してみると、B[N] = -1294967296 となっており、その時点でプログラムの誤りがあることがわかります。

もう少し分かりやすく説明しましょう。仮に 100 行のプログラムがあったとして、50 行目にデバッグ出力を追加したとします。そのとき、

• もしデバッグ出力の値がおかしかった場合はプログラムの前半にバグがある
• そうでない場合はプログラムの後半にバグがある

ということが分かるのです。このように、cout / printf などを使うと効率的に誤った箇所を見つけることができます。（この種のデバッグ方法を print デバッグと呼びます）

それに関連して、Visual Studio などブレークポイントが使えるエディタでは、print デバッグの代わりにブレークポイントを用いたデバッグを行うことも可能です。下図は本節で紹介したサンプルプログラムのバグ取りをする様子を示しています。

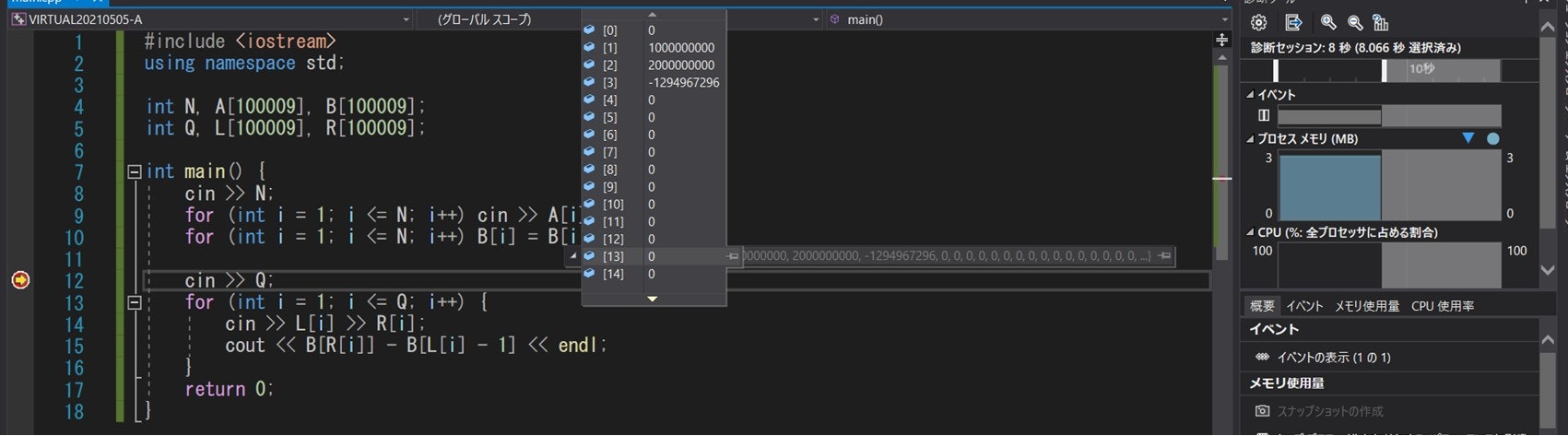
4-5. コードをざっと読む（重要度：3）

では、4-2. 節や 4-3. 節で説明したように、サンプルを含む複数のテストケースで試しても、誤答ケースが見つからなかったとしましょう。どうやってバグの手がかりを掴むことができるのでしょうか。1 つのアイデアとして、次のものが挙げられます。

コードをざっと読んで、ミスがないか確認する

しかし、ただプログラムを読むだけでは簡単に見つからない場合も多いので、主に

• 2 章｜そもそもどんなバグが起こるのか？ ～典型パターン 10 個を整理～

に載っているものに注意しながらバグを探すと、効率的です。

具体的に注意するべき点

特に、次のような点に注目すると、バグが特定できる可能性が高まります。

• 添え字ミスをしていないか？（i と j を逆にしていないか？）
• 境界処理をバグらせていないか？（>= と > を逆にしていないか？）
• 配列外参照をしていないか？（小さいケースでは気づかないバグ）
• 計算途中でオーバーフローを起こしていないか？
• 上限下限の設定は正しいか？（例えば、A[1], A[2], ..., A[N] の最大値を求めるとき、Answer の初期値を A[i] としてあり得る最小値以下にしているか？¹⁰）

---

ここまで、もしバグった場合にどう対処すれば良いのかを解説しました。しかし、目に付きにくいバグの場合、ここまで 5 つの手段を尽くしてもなお、そもそも不正解となる入力データ（誤答ケース）すら得られないこともあります。私自身の経験でも、発生させたバグのうち 20 回に 1 回程度は、ここまでの手順で解消することができませんでした。

しかし、まだ最終手段が残されています。これを 5 章で紹介したいと思います。

5. ステップ C｜最終手段・ランダムチェッカーのすすめ

4 章ではデバッグの方法について解説しましたが、残念ながら 5 つの手段すべてを検討しても原因が分からず、八方塞がりになってしまうこともあります。しかし、

ランダムチェッカーを作る

という最強の対処法を使うと、今まで全く目に見えなかったバグもほとんど解消できてしまうのです。本章ではそれについて、実際にランダムチェッカーを書いてみる「実演セクション」を交えながら、分かりやすく解説したいと思います。

5-1. ランダムチェッカーとは？

まず、ランダムチェッカーとは次のようなものです。

自動でランダムケースをたくさん（1000 個から 100 万個オーダーで）生成することで、自分のプログラムと実際の答えが異なるような入力データを探すプログラム。

したがって、ランダムチェッカーを動かすためには、主に「自分のプログラム」「計算に時間がかかるが正しいプログラム（いわゆる愚直解）」「ランダムにケースを生成するプログラム」の 3 つが必要です。

ランダムチェッカーのひな型

もう少しイメージを分かりやすくするために、書き方の一例を紹介します。なお、

• solve 関数は自分のプログラム（例：時間計算量 $O(N \log N)$ など）
• solve_Jury 関数は遅いが正しいプログラム（例：時間計算量 $O(N^2)$ や $O(2^N)$ など、解法が自明であるもの）であり、正しい答えを返すことが想定されている
• random_generate 関数はランダムにケースを生成するプログラム

となっています。

#include <iostream>
#include <vector>
using namespace std;

void random_generate(int N, vector<int> &A, vector<int> &B) {
    // ここでランダム生成をする。例えば次のような感じ。
    // for (int i = 0; i < N; i++) A[i] = rand() % 10 + 1;
    // for (int i = 0; i < N; i++) B[i] = rand() % 10 + 1;
}

int solve(int N, vector<int> A, vector<int> B) {
    // ここに自分のプログラムを書き、自分の答えを返す。
}

int solve_Jury(int N, vector<int> A, vector<int> B) {
    // ここに「遅いが正しいプログラム」を書き、正しい（と想定される）答えを返す
}

int main() {
    for (int t = 1; t <= 1000; t++) {
        int N = 8; // 入力データのサイズ（適当に決めて良い）
        vector<int> A(N), B(N); // プログラムで使用する変数
        random_generate(N, A, B);
        int J1 = solve(N, A, B);
        int J2 = solve_Jury(N, A, B);
        if (J1 != J2) {
            cout << "Wrong Answer on Test #" << t << endl;
            cout << "Jury = " << J2 << ", Output = " << J1 << endl;
            // テストケースを出力
            return 0;
        }
    }
    cout << "Yay!" << endl;
    return 0;
}

5-2. 実戦編：実際にランダムチェッカーを書いてみよう

ランダムチェッカーは確かに最強の手段ではありますが、実際に一度書いてみなければ慣れることはできません。また、AtCoder などのプログラミングコンテストでは「解くまでにかかる時間」も重要であるため、ランダムチェッカーを書くためにかけられる時間は僅か 5 ～ 10 分程度とシビアです。

そこで本節では、書き方に慣れてもらうために、実際にランダムチェッカーを書いてみることにします。（なお、書き方は人によって異なるため、既に自己流の書き方を持っている方は、実戦編を読み飛ばしても構いません。）

今回扱う問題

本節では、次の問題を扱います。

長さ $N$ の数列 $A = (A_0, A_1, ..., A_{N-1})$ が与えられます。$0 \leq i \lt j \leq N-1$ となるように $(i, j)$ を選んだとき、$A_j - A_i$ としてあり得る最大値はいくつですか？
制約：$2 \leq N \leq 10^5, 1 \leq A_i \leq 10^9$

例えば、$N = 6, A = (3, 1, 4, 1, 5, 9)$ の場合、$(i, j) = (1, 5)$ を選んだとき、最大値 $A_5 - A_1 = 9 - 1 = 8$ が達成でき、これが答えとなります。

今回扱うプログラム

本節では、次のプログラムのデバッグをすることを考えます。

int solve(int N, vector<int> A) {
    int Answer = 0, CurrentMin = A[0];
    for (int i = 1; i < N; i++) {
        Answer = max(Answer, A[i] - CurrentMin);
        CurrentMin = min(CurrentMin, A[i]);
    }
    return Answer;
}

ステップ 1｜遅くて正しい解法を書く

皆さんが最初に思いつく解法の 1 つとして、次のものが挙げられます。

• $(i, j)$ $[1 \leq i \lt j \leq N]$ の組を全探索する

これは全通り調べ上げているので、解法の正当性に疑いの余地がありません。そこで、この「全探索アルゴリズム」を関数 solve_Jury に組み込みましょう。実際に、solve_Jury(6, {3, 1, 4, 1, 5, 9} を呼び出すと 8 が返ってくるのが分かると思います。

int solve_Jury(int N, vector<int> A) {
    int Answer = -(1 << 30);
    for (int i = 0; i < N; i++) {
        for (int j = i + 1; j < N; j++) Answer = max(Answer, A[j] - A[i]);
    }
    return Answer;
}

ステップ 2｜ランダムケース生成を書く

次に、どのようにしてランダムケースを生成すれば良いのでしょうか。この部分は勘に頼るしかないのですが、N = 5 程度でも誤答ケースが存在しそうなので、とりあえず $N = 5$ にセットしましょう。また、A[i] も 1 以上 10 以下のランダムな値にしてみましょう。

例えば std::rand() 関数を使うと、次のように実装できます。

void random_generate(int N, vector<int> &A) {
    for (int i = 0; i < N; i++) {
        A[i] = rand() % 10 + 1;
    }
}

ステップ 3｜main 関数を書く

次に、solve・solve_Jury・random_generate など様々な関数を呼び出す main 関数の部分を書いてみましょう。

• テストケース数を 1000 に設定する
• 誤答ケースを問題で指定されている入力形式で出力した方が便利なので、それを出力する

といった項目を考慮した上で 5-1. 節のひな型に従って書くと、次のようになります。

int main() {
    for (int t = 1; t <= 1000; t++) {
        int N = 5;
        vector<int> A(N);
        random_generate(N, A);
        int J1 = solve(N, A);
        int J2 = solve_Jury(N, A);
        if (J1 != J2) {
            cout << "Wrong Answer on Test #" << t << endl;
            cout << "Jury = " << J2 << ", Output = " << J1 << endl;
            // 誤答ケースの出力
            cout << N << endl;
            for (int i = 0; i < N; i++) {
                if (i >= 1) cout << " ";
                cout << A[i];
            }
            cout << endl;
            return 0;
        }
    }
    cout << "Yay!" << endl;
    return 0;
}

ステップ 4｜ランダムチェッカーを実行してみる

最後に、自分で作ったランダムチェッカーを実行してみましょう。乱数を用いているので、実行結果は環境によって異なる場合がありますが、例えば次の結果が得られます。

Wrong Answer on Test #41
Jury = -1, Output = 0
5
10 7 6 2 1

このように、$N = 5, A = (10, 7, 6, 2, 1)$ という入力データで、本来ならば -1 と返すべきところを 0 と返しており、誤答となっていることが判明しました。

あとは、4 章の内容に従ってバグの箇所を探せば、solve 関数の前半で Answer = 0 に初期化してしまったことが問題だと分かります。そして、Answer = -(1 << 30) などに修正すると、バグがついに解消し、AC（正解）を得ることができるのです。

5-3. 理論編：ランダムチェッカーを実行するための注意点

いくらランダムチェッカーが最強であるとはいえ、そもそもランダムチェッカーの方が間違っていたら元も子もないです。そこで本章の最後に、注意点をいくつか記したいと思います。

注意点 1：適切に初期化をしていますか？

ランダムチェッカーでは $10^3 \sim 10^6$ 個のケースを生成し、それぞれについて実行します。つまり、2-9. 節で紹介した「複数テストケース形式」に相当します。

そこで、もし初期化を行わなかった場合、前の計算結果が後の答えに影響してしまうため、solve 関数や solve_Jury 関数が想定される答えを返さなくなってしまう可能性があります。そのため、テストケースの実行前に、すべてのグローバル変数を初期化するなどの対応が必要になってきます。

注意点 2：小さいケースを試していますか？

大半のバグでは $N$ が大きいほど誤答を出す確率が高まりますが、必ずしもそうとは限りません。例えば、5-2. 節に記したランダムチェッカーのサンプルプログラムを $N = 20$ で実行してみましょう。結果は次のようになります。

Yay!

残念ながら誤答ケースは 1 つも見つかりませんでした。理論的に検証してみると、$A_1 > A_2 > \cdots > A_N$ の場合にしか誤答を出さないため、誤答を出す確率は $1 \div N!$ 以下であることが分かります。このような場合、$N = 1, 2, 3$ など小さいテストケースを試すことも重要です。¹¹

注意点 3：C++ の rand 関数のワナ

実は Visual Studio で実行される rand 関数にはワナがあって、$0$ 以上 $32767$ 以下の整数しか返しません。したがって、例えば A[i] = rand() % 1000000000 + 1 とプログラムを書いても、A[i] が $32769$ 以上の値になることはなく、$[1, 10^9]$ の一様乱数としての機能を果たしません。このような点にも注意が必要です。

注意点 4：「遅いが正しい解法」は本当に正しいですか？

そもそも solve_Jury 関数で扱う解法は正しい答えを返すことが想定されているため、これを間違えた場合、正しくデバッグができません。したがって、次の点に注意が必要です。

• solve_Jury 関数を丁寧に書く
• 誤答ケースが見つからない場合、遅い解法の正当性やバグを疑う
• 誤答ケースが見つかっても、実は遅い解法が間違っている可能性を疑う

---

ここまで、ランダムチェッカーを用いたデバッグの方法について解説しました。やはり適切な使い方をすれば、この方法は最強に近く、私も競プロを始めてから 5 年間で数百回以上のバグを経験しましたが、最終手段であるランダムチェッカーですら解決できなかったことは僅か 2 件しかありませんでした。

しかし、それでも解決できない非常にアンラッキーなことが起こる可能性は、ゼロではありません。6 章では、これが起こる原因について紹介し、本記事を締めたいと思います。

6. ステップ D｜それでも原因が見つからない場合

本記事では、5 章までに次の内容を紹介してきました：

• 3 章｜バグのないプログラムを書く方法
• 4 章｜バグを発生させたらどうすれば良いか？
• 5 章｜最終手段・ランダムチェッカーのススメ

しかし、本当にごく稀ですが、ここまでの手段を尽くしても解決できないことがあります。

そこで記事の最後に、このような事象が起こる主な原因について、2 つのパターンに分けて解説したいと思います。

6-1. 問題文を誤読している

バグが解決できない原因として、問題文を誤読しているケースが考えられます。

この場合、solve 関数・solve_Jury 関数両方が「間違って思い込んだ問題文」をベースにして書かれるため、整合性があります。したがって、ランダムチェッカーではすべて正解してしまうのです。一方、実際に提出してみると、当然ですが WA（不正解）になってしまいます。

そこで、もしランダムチェッカーでも解決できない場合、問題文をもう一度読み、誤読していないか再確認することが大切です。なお、問題文が曖昧で分かりにくいと感じたときは、AtCoder の場合「質問」機能を使って問題文の意図を聞くことができます。

6-2. 実行環境の違いが原因で手元で正しく動いてしまう

もう一つの原因は「実行環境」です。
AtCoder と手元では実行環境が違う可能性があります。例えば C++ の場合、

• AtCoder では「GCC 9.2.1」
• Visual Studio では「Microsoft Visual C++」

が使われています。

もし実行環境が違うと、例えば未定義動作を起こしたときの挙動が異なる場合があるため、手元では正しく動くのに AtCoder では正しく動かない最悪のシナリオでは、バグの原因が分からずにコンテストが終わってしまうのです。

そこで、次のような対処法が考えられます。

AtCoder のコードテストを利用してランダムチェッカーを動かす

問題文を誤読していないにも関わらず、ランダムチェッカーで誤答ケースが見つからない場合は、この方法を使っても良いかもしれません。

7. おわりに

私はプログラミングにおいて、デバッグ力はとても重要だと考えています。バグの少ないプログラムを書けるか、そしてどの程度高速にバグを発見できるか。これらが「問題を解く速度」に直接影響し、プログラミングコンテストでのパフォーマンス、ひいてはプログラマとしての技術力にまで直結すると思います。

そこで、アルゴリズムなどの実装において発生しやすいバグ、そしてデバッグの手順をまとめることで、少しでも皆さんのスキルアップに貢献できればと思い、本記事を書くことにしたので、この記事が一人でも多くの方の役に立つことができれば、とても嬉しい気持ちです。

最後に、これは大学 1 年生が書いた記事なので、分かりにくい部分も多かったと思われますが、最後までお読みいただきありがとうございました。

8. 参考文献・参考資料

今後、さらにデバッグ力を磨きたいと考えている読者のために、関連する記事をいくつか載せておきます。特に一番上の記事は、バグの原因がたくさんリストアップされているので、非常に参考になると思います。

• Motsu_xe のブログ｜バグった原因集
• knshnb のブログ｜競技プログラミングで C++ を書く際に意識していること
• ヘクトのメモ｜競プロ初心者だった頃の注意すべき点を列挙する
• Qiita｜実装力で戦える！ ～競プロにおける実装テクニック 14 選

---

1. 例えば AtCoder Beginner Contest 176 B - Multiple of 9 などの問題では、string 型で整数を入力しなければなりません。なお、別の手段として多倍長整数を使うという方法もあります。 ↩

2. テストケース数が非常に多く、かつ $N$ の値がケースによってバラついているような問題の場合、初期化（init 関数の処理）のせいで実行時間超過（TLE）を起こす場合もあります。対処法としては、「前のテストケースの $N$ の値をメモしておいて、前のテストケースで使った部分だけを初期化する」「$N$ を入力してから init 関数を呼び出し、そのテストケースの実行に必要な部分だけを初期化する」などが考えられます。 ↩

3. ナップザック問題という有名問題です。動的計画法により、高速に解くことができます。 ↩

4. このように、直感に頼った未証明の Greedy は危険です。（リンク） ↩

5. 競技プログラミングでは、間違った解法を嘘解法と呼ぶこともあります。 ↩

6. ただし、コンテスト時間には限りがあるので、証明を考えても思いつかなかった場合、賭けに出て実装するのも手段の 1 つです。 ↩

7. 例えばこのソースコードでは、61 行目が本来 for (int i = A.size() - 1; i >= 0; i--) となっているべきところを間違えて for (int i = 0; i < A.size(); i++) と書いてしまっていますが、それでも 43 ケース中 40 ケースで正解が得られています。 ↩

8. 人によっては、「サンプル試す時間も無駄だから節約したい…」と思うかもしれませんが、私の経験上サンプルが一発で合う確率は 3 割程度である一方、サンプルで全部合わせた後に提出をして AC が得られる確率は 6 割程度と差があります。したがって、提出前に入出力例を試していない参加者は、それをするだけで相当 WA の数が減らせると思います。 ↩

9. AtCoder Beginner Contest 199 における WA の提出をランダム抽出したところ、107 件中 49 件がサンプルケースに 1 つ以上の不正解が見られました。コンテスト時間中の提出に絞っても、62 件中 25 件（40%）と非常に高い数値が出ています。 ↩

10. 例えば A[1] = -100, A[2] = -100 で Answer の初期値が -50 だった場合を考えてみましょう。そのとき、Answer = max(Answer, A[1])・Answer = max(Answer, A[2]) という処理を行った後の Answer の値は -50 のままであり、正しく求まっていません。 ↩

11. 他にも、2-6. 節で述べたコーナーケースや、「$A_i$ が全部小さい場合」「$A_i$ が全部同じ場合」「$A_i$ が大きくてオーバーフローを誘発する場合」などのテストケースを試すことも重要です。 ↩