Qiita記事データで技術の寿命を分析する 〜コンテンツログを用いた生存時間分析〜

本記事はNTTドコモSI部アドベントカレンダー19日目の記事です．

こんにちは! 先読みエンジンチームの橋本です. 業務ではエージェントサービスのためのパーソナルデータ解析の技術開発に取り組んでます．

本記事では，Qiita投稿記事データに生存時間分析の適用し，コンテンツ(継続的な記事投稿)の寿命を定量的に評価する方法を紹介します．

生存時間分析とは，イベント発生までの期間とイベントとの関係を分析する手法です．一般的に，医学分野における患者の死亡イベントまでの期間(人の寿命)や，工学分野における部品の故障イベントまでの期間(部品の寿命)の分析に使われます．今回はQiita投稿データにおいて，ユーザが特定の技術の記事の継続的な投稿をやめたことをイベントの発生として技術投稿の寿命の分析をしようと思います!

生存時間分析を用いることで，そのコンテンツの寿命が長い/短いものなのか，あるいはコンテンツの利用率の減少が緩やか/急なのかを評価することができます．評価結果の利用先として，コンテンツ分類タスクの特徴量作成や，コンテンツ利用履歴を用いたユーザ分類タスクの特徴量作成，あるいはコンテンツレコメンド施策に向けた意思決定など,いろいろ考えられます．

生存時間分析についての詳細は，下記の記事および書籍が参考になると思います．

• https://qiita.com/saltcooky/items/409329485be499a5b270
• https://note.com/maxwell/n/nc78c55afe944
• https://www.kyoritsu-pub.co.jp/bookdetail/9784320110359

分析の流れ

本記事の分析のざっくりとした流れは下記のとおりです．

1. データの前処理: 全ユーザに対して，特定のタグのついたQiita記事を投稿し続けている期間と，投稿をやめたかのフラグを算出する
2. ワイブルモデルへの適用: 上記を入力データとしてワイブルモデルをfitさせ(ワイブルモデルのパラメータを推定する)，ワイブルモデルから得られる生存率曲線を出力する．
3. タグごとの生存率の比較: 複数のタグ(技術)に対して上記を実施し生存率曲線のパラメータを比較してみる．

記事中のプログラムの実行環境はPython3.6, macOS 10.14.6です．また，lifelines 0.22.9という生存時間分析ライブラリをつかっていきます．

データセットについて

本記事では，下記で得られたQiitaデータセットを利用しております．
Qiitaの投稿記事からデータセット作った

本データセットはQiitaで提供されているAPIから取得されたユーザの記事投稿履歴のデータセットです．2011年から2018年までの投稿履歴が確認できます．
今回の分析を実施する上で

• ユーザのコンテンツ履歴であること．
• ユーザが定期的に同じコンテンツ(今回は同じ記事タグ)を利用する形のものであること．

の2つの条件を満たしておるため，本データを採用しました．

pandas dataframeでデータを読み込むと下記のようになります．

import pandas as pd

df = pd.read_csv('qiita_data1113.tsv', sep='\t')
df.head()

created_at	updated_at	id	title	user	likes_count	comments_count	page_views_count	url	tags
2011-09-30T22:15:42+09:00	2015-03-14T06:17:52+09:00	95c350bb66e94ecbe55f	GentooかわいいよGentoo	{'description': ';-)',...	1	0	NaN	https://...	[{'name': 'Gentoo', 'versions': []}]
2011-09-30T21:54:56+09:00	2012-03-16T11:30:14+09:00	758ec4656f23a1a12e48	地震速報コード	{'description': 'Emi Tamak...	2	0	NaN	https://...	[{'name': 'ShellScript', 'versions': []}]
2011-09-30T20:44:49+09:00	2015-03-14T06:17:52+09:00	252447ac2ef7a746d652	parsingdirtyhtmlcodesiskillingmesoftly	{'description': 'githubをギッハブと呼ぶな...	1	0	NaN	https://...	[{'name': 'HTML', 'versions': []}]
2011-09-30T14:46:12+09:00	2012-03-16T11:30:14+09:00	d6be6e81aba24f39e3b3	Objective-Cのクラスの実装のなかで以下の変数xはどういう扱いになるんでしょうか...	{'description': 'こんにちは。はてな...	2	1	NaN	https://...	[{'name': 'Objective-C', 'versions': []}]
2011-09-28T16:18:38+09:00	2012-03-16T11:30:14+09:00	c96f56f31667fd464d40	HTTP::Request->AnyEvent::HTTP->HTTP::Response	{'description'...	1	0	NaN	https://...	[{'name': 'Perl', 'versions': []}]

ちなみに，各記事においてtagsカラムから最大3つのタグをを抽出して，全体での個数をみたランキングは下記の形になります．

	index	tag
0	JavaScript	14403
1	Ruby	14035
2	Python	13089
3	PHP	10246
4	Rails	9274
5	Android	8147
6	iOS	7663
7	Java	7189
8	Swift	6965
9	AWS	6232

分析処理

1. 前処理

上記のデータセットを読み込んだDataFrameから必要なデータを抽出します．

df_base = <get tags>
df_base.head()

user_id	time_stamp	tag
kiyoya@github	2011-09-30 22:15:42+09:00	Gentoo
hoimei	2011-09-30 21:54:56+09:00	ShellScript
inutano	2011-09-30 20:44:49+09:00	HTML
hakobe	2011-09-30 14:46:12+09:00	Objective-C
motemen	2011-09-28 16:18:38+09:00	Perl
ichimal	2011-09-28 14:41:56+09:00	common-lisp
l_libra	2011-09-28 08:51:27+09:00	common-lisp
ukyo	2011-09-27 23:57:21+09:00	HTML
g000001	2011-09-27 22:29:04+09:00	common-lisp
suginoy	2011-09-27 10:20:28+09:00	Ruby

各レコードからuser_id, time_stampとしてcreated_at，tagを抽出しました．
tagが複数ついているものに関しては5つまでとりだし,それぞれ1つのレコードとしてconcatしました．
なお，tagの表記ゆれ(golangとGo，RailsとRubyOnRailsなど)は特に考慮しておりません．

lifelinesのワイブルモデルに入力するためにデータの形式を生存期間とイベントフラグの２カラムのデータに変換します．本データからは明確なイベント(記事投稿をやめた)や生存時間(継続的な記事投稿をしつづけている期間)が分からないため，独自に定義する必要があります．

イベントについて，本項では下記の2つの条件が満たされた場合にイベント発生と定義することにします．

1. 隣り合う2つの投稿の間の期間がθ日以上だった場合にイベント発生
2. 観測期間の締め切りと直近の投稿の期間がθ日以上だった場合にイベント発生

なお，観測期間の締め切りと直近の投稿の期間がθ日未満だった場合，観測打ち切りとしてあつかいます．

少しわかりにくいので，図で説明します．

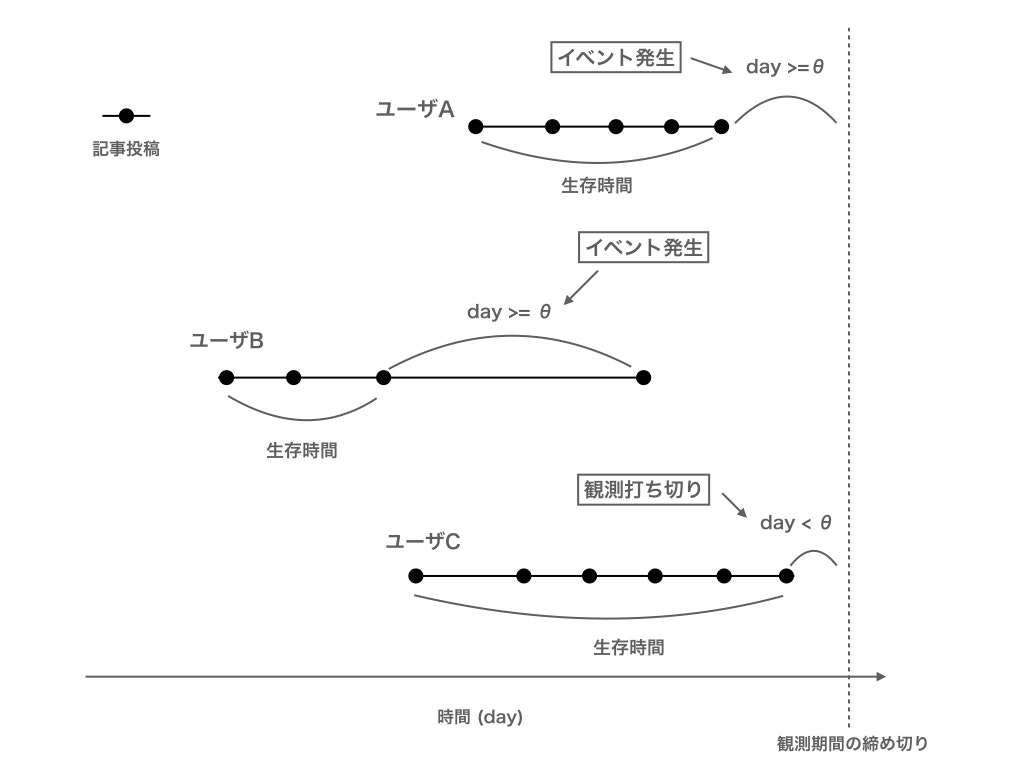
上記の図は，3ユーザに対して，記事投稿のタイミングを時系列に並べたものを示しております．
ユーザAは観測期間の締め切りと直近の投稿の期間がθ日以上です．したがって最終投稿の後でイベント発生という形になります．ユーザBは直近の2つの投稿の期間がθ日以上です．この場合もイベント発生として判断します．ユーザCは全て隣り合う2つの投稿の間の期間がθ未満かつ，観測期間の締め切りと直近の投稿の期間がθ日未満です．したがって，観測打ち切りとしてあつかいます．
また，生存時間についてはイベント発生までの期間または観測期間の締め切りまでの期間を生存時間とします．

今回は以上のルールでイベントの発生有無および生存時間を決定することにしました．
上記ロジックをmake_survival_dataset()として定義して実装すると下記のようになります．今回はθ=365日とします．また，観測締め切りとして2018/12/01を指定します．引数には特定のタグでフィルタしたDataFrameを入力する想定です．

import datetime
import pytz

def make_survival_dataset(df_qiita_hist, n = 365):
    id_list = []
    duration_list = []
    event_flag_list = []
    
    for index, (userid, df_user) in enumerate(df_qiita_hist.groupby('user_id')):
        # 観測の締め切りを末尾に追加する
        dt = datetime.datetime(2018, 12, 1, tzinfo=pytz.timezone("Asia/Tokyo"))
        last = pd.Series(['test', dt, 'last'], index=['user_id', 'time_stamp', 'tag'], name='last')
        df_user= df_user.append(last)
        
        # 隣り合う２つの投稿の間の期間を算出する (リストの先頭はNoneになる．)
        day_diff_list = df_user.time_stamp.diff().apply(lambda x: x.days).values
        
        # リストの長さが2以下のものは計算対象から外す．
        if len(day_diff_list) <= 2:
            continue
            
        # イベント発生するか否かを探索する．
        event_flag = False
        # イベント発生までの期間を計算するリスト
        day_list = []
        
        for day in day_diff_list[1:]:
            if day >= n:
                event_flag = True
                break
        
            day_list.append(day)
            
        # イベント発生までの期間を計算
        s = sum(day_list)
        
        # 期間が0のものは対象外とする
        if s == 0:
            continue
        
        # DataFrameを作成
        id_list.append(userid)
        duration_list.append(s)
        event_flag_list.append(event_flag)
        
        
    return pd.DataFrame({'userid':id_list, 'duration':duration_list, 'event_flag': event_flag_list})

Pythonタグがついたレコードを抽出し，make_survival_datasetに入力してみます．

df_python = df_base[df_base['tag'] == 'Python'].sort_values('time_stamp')
df_surv = make_survival_dataset(df_python, n=365)
df_surv.head()

userid	duration	event_flag
33yuki	154.0	False
5zm	432.0	False
AketiJyuuzou	57.0	True
AkihikoIkeda	308.0	False
Amebayashi	97.0	True

これで，ワイブルモデルへの入力するデータはできました．

2. ワイブルモデルへの適用

上記で作成したデータをワイブルモデルに入力し，パラメータのフィッティングおよび生存率曲線のプロットを実施します．
ここではPythonに加えて，Rubyタグが付いたデータをプロットしてみます．

import lifelines
%matplotlib inline
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'IPAexGothic'

_, ax = plt.subplots(figsize=(12, 8))

# Python
name = 'Python'
df_surv = make_survival_dataset(df_base[df_base['tag'] == name].sort_values('time_stamp'), n=365)
wf = lifelines.WeibullFitter().fit(df_surv['duration'], df_surv['event_flag'], label=name)
wf.plot_survival_function(ax=ax, grid=True)

# Ruby
name = 'Ruby'
df_surv = make_survival_dataset(df_base[df_base['tag'] == name].sort_values('time_stamp'), n=365)
wf = lifelines.WeibullFitter().fit(df_surv['duration'], df_surv['event_flag'], label=name)
wf.plot_survival_function(ax=ax, grid=True)

ax.set_ylim([0, 1])
ax.set_xlabel('生存期間(日)')
ax.set_ylabel('生存率')

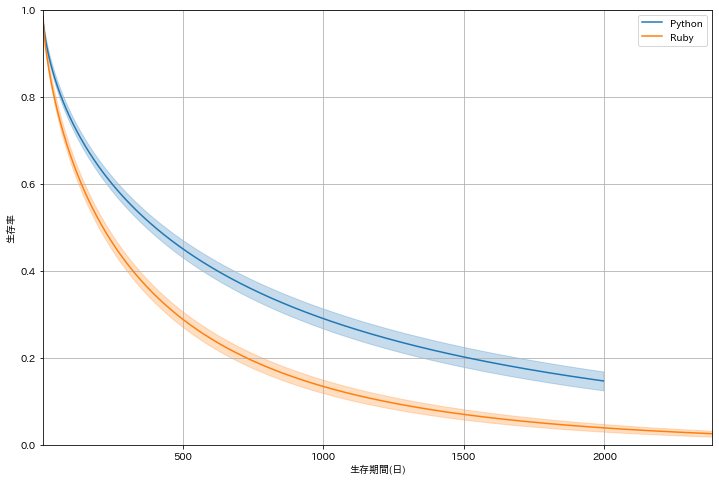
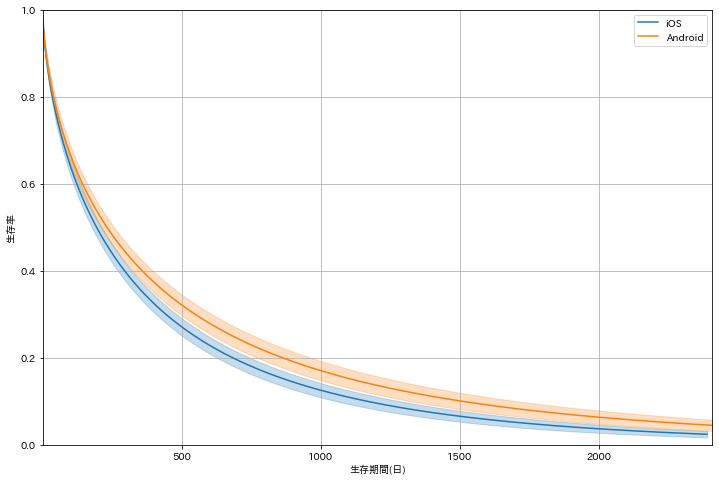
縦軸は日数，縦軸は生存率(投稿し続けているユーザの割合)です．全体として，日数が進むに連れて生存率が下がっていることがわかります．Pythonに着目すると，1500日のタイミングで，生存率がちょうど0.2を下回っていることが確認できます．これは，投稿開始から1500日後になると20%の人がその後も投稿を続けることを意味してます．一方で残りの80%は継続的な投稿をやめてしまうことを意味しています．
PythonとRubyを比較する1500日後に10%ほど差があることがわかります．これを見る限りでは，**総合的にRubyの記事よりものPythonの記事の方が生存時間が長く，継続的な記事投稿がされる傾向があるといえます．**Pythonの寿命が長い背景には，近年の機械学習/データ分析のツールとしての需要増加が影響していると思われます．

このように，コンテンツログに対しイベント発生と生存時間を定義し生存時間分析を実施することで，コンテンツの生存時間を比較することができます．

3. タグごとの生存率曲線のパラメータ比較

lifelinesのドキュメントによると生存率曲線は下記の数式に基づいてプロットされています．

$$ S(t) = \exp(-(t/\lambda)^{\rho}) \ where\ \lambda > 0, \rho > 0 $$

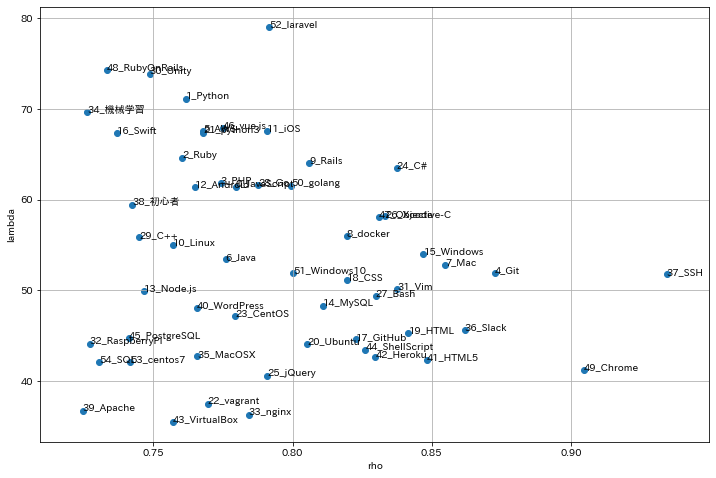
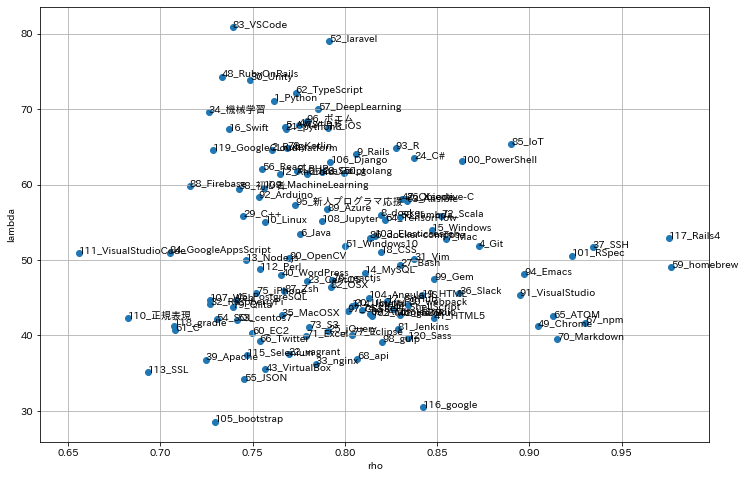
生存率曲線はパラメータλとρに依存しており，Weibull Fitterのfit関数は上記のパラメータを算出する形になっております．なので，WeibullFitterから得られるλとρの値を2次元グラフにプロットすることで，タグごとの生存率曲線の類似度を目視で確認することができます．

データセットの中で投稿ユーザ数が1000人以上のタグに絞って，プロットしてみました．

縦軸にλ，横軸にρがプロットしてあります．

一般的に，λの値が大きいほど生存時間が長く，ρの値が大きいほど時間経過ともに生存率曲線の傾きが急になっていく傾向があります．
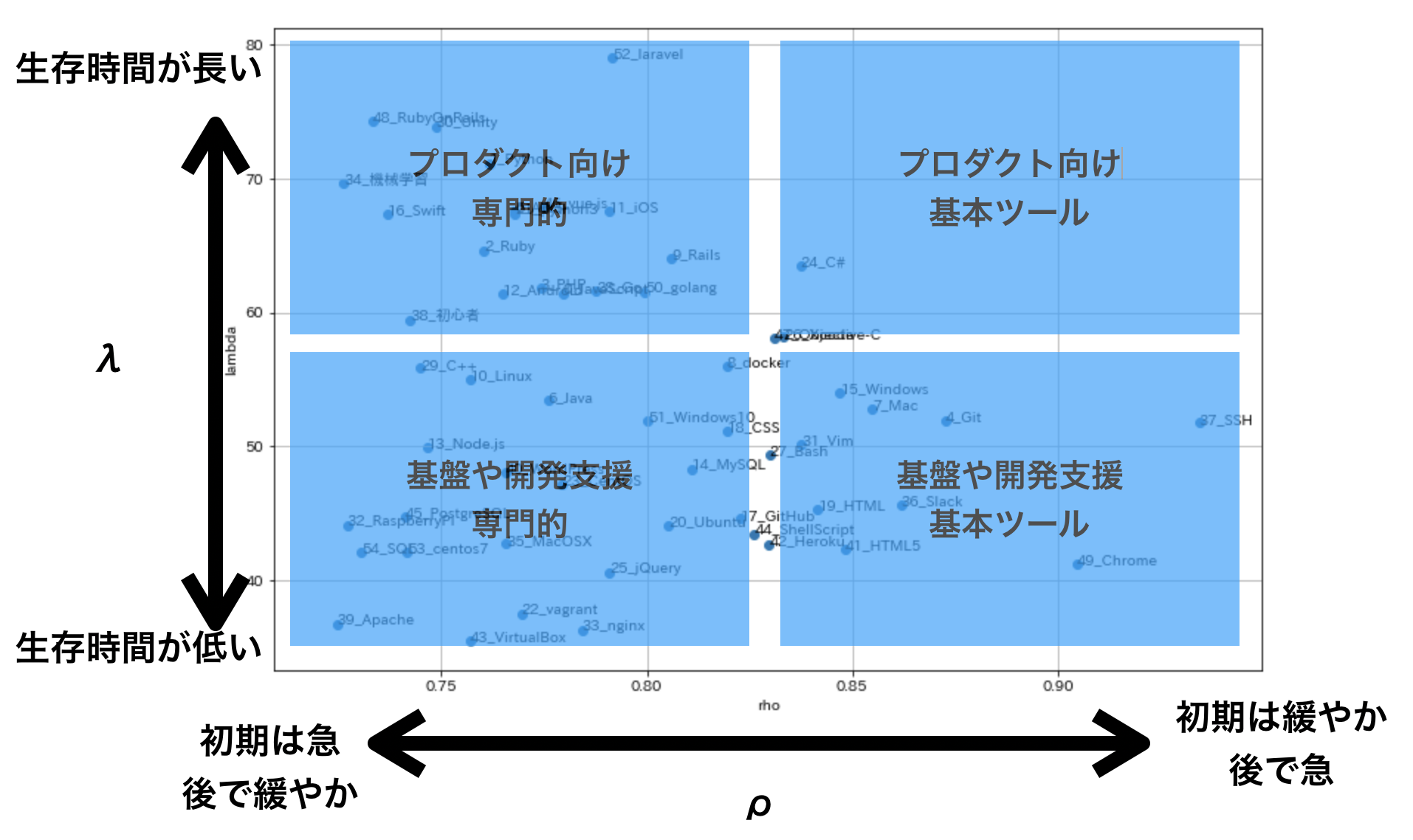
ざっくりとλとρの大小で分類してみると下記の感じでしょうか

• λが大: 生存時が長い

  • PHP(およびLaravel),Ruby(およびRails)，C#，iOS，Androidなど
  • プロダクトに使われることが多く(ユーザが多い?)プログラミング言語（およびフレームワーク)やモバイル開発が多い印象
  • プロダクトに使われる言語やフレームワークなのでネタが多く記事投稿が継続しやすい
  • アップデートによる機能変化のインパクト度合いなどにも関係してそう

• λが小: 生存時間が短い

  • CentOS，Ubuntu，PostgreSQL，Nginx，Git，Slackなど
  • OSやミドルウェアなどの開発基盤ツールやGitやSlackなどの開発支援のツールが集中している印象
  • 基盤部分なのでネタが比較的少ないため記事投稿が短期的になりやすい

• ρが大: 時間経過ともに生存率曲線の傾きが急になっていく

  • SSH，Chrome，Git，Slack，Mac，Windowsなど
  • 基本的なツールが集中している印象
  • 基本ツールに関する記事は入門的な記事投稿が多く，投稿開始後は継続的な投稿が少し続くがしばらくたつと減少する

• ρが小: 時間経過ともに生存率曲線の傾きが緩やかになっていく

  • プログラミング言語，ミドルウェア，Linux系OSなど
  • 比較的専門性が高いツール(技術)が集中している印象.
  • 専門性が高いツール(技術)の記事は投稿開始後すぐにやめやすいが継続的に投稿していく人もいる

まとめると下記の図のようになります．

だいたいの物に関しては解釈と合っている(?)印象です．
パラメータの違いが，実際の技術の種類とも関係があっておもしろいですね．
C♯とObjective-C などちょっと微妙な部分もありますが...

まとめ

Qiita記事データに対して生存時間分析を実施し，生存時間の長さと生存率曲線の傾きの変化度合いの2つの観点でコンテンツを分類しました．ざっくりとした解釈でしたがパラメータの違いと技術の種類とも関係がありそうなことがわかりました．
本記事で紹介した内容は他のコンテンツログにでも適用できる方法だと思います．コンテンツ利用ログに触れる機会がある方は参考にしてみていただければと思います．
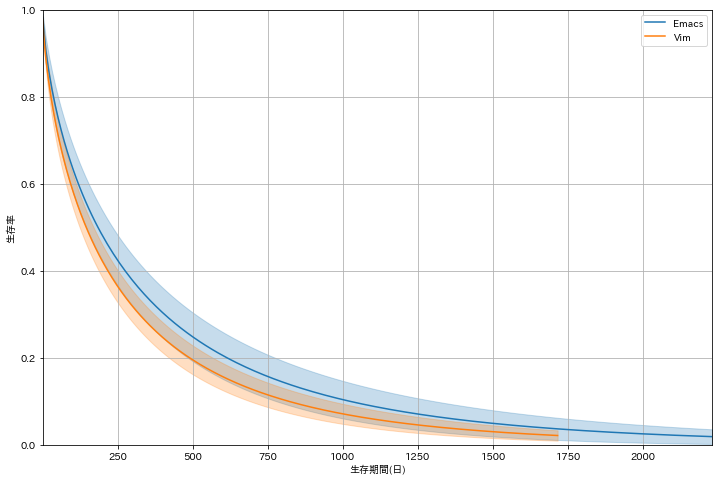
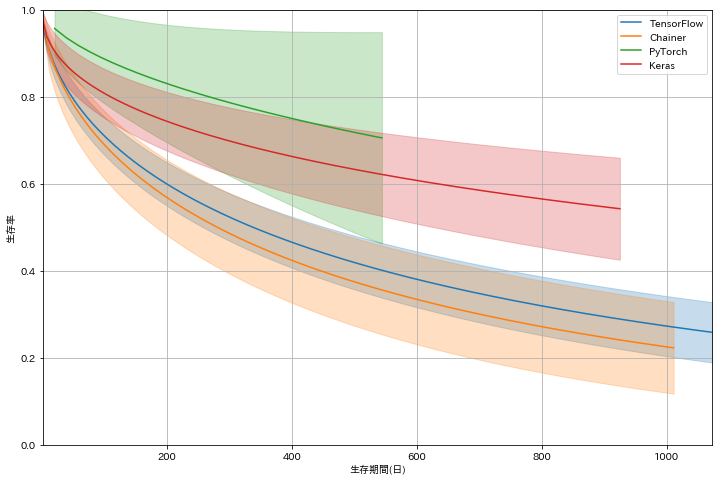
最後におまけの分析結果をいくつか共有して終わりにします．
それでは，よいお年を〜

おまけ

iOS V.S. Android

Emacs V.S. Vim

代表的なDeepLearningフレームワーク

投稿ユーザ数が500人以上でパラメータプロット