Go to Qiita Advent Calendar 2024 Top
LoginSignup
88
63

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 3 years have passed since last update.

NTTドコモ R&D Advent Calendar 2020

Day 25
@dcm_demizu

強化学習コンペで交通×AIに挑戦：KDDCUP2020 RL Track 世界3位獲得！

Last updated at Posted at 2020-12-24

はじめに

Happy Holidays 🎉

NTTドコモの出水です．最終日の本記事では，ドコモR&Dチームで参加した強化学習コンペティションの取組みと活用方法をお届けします！

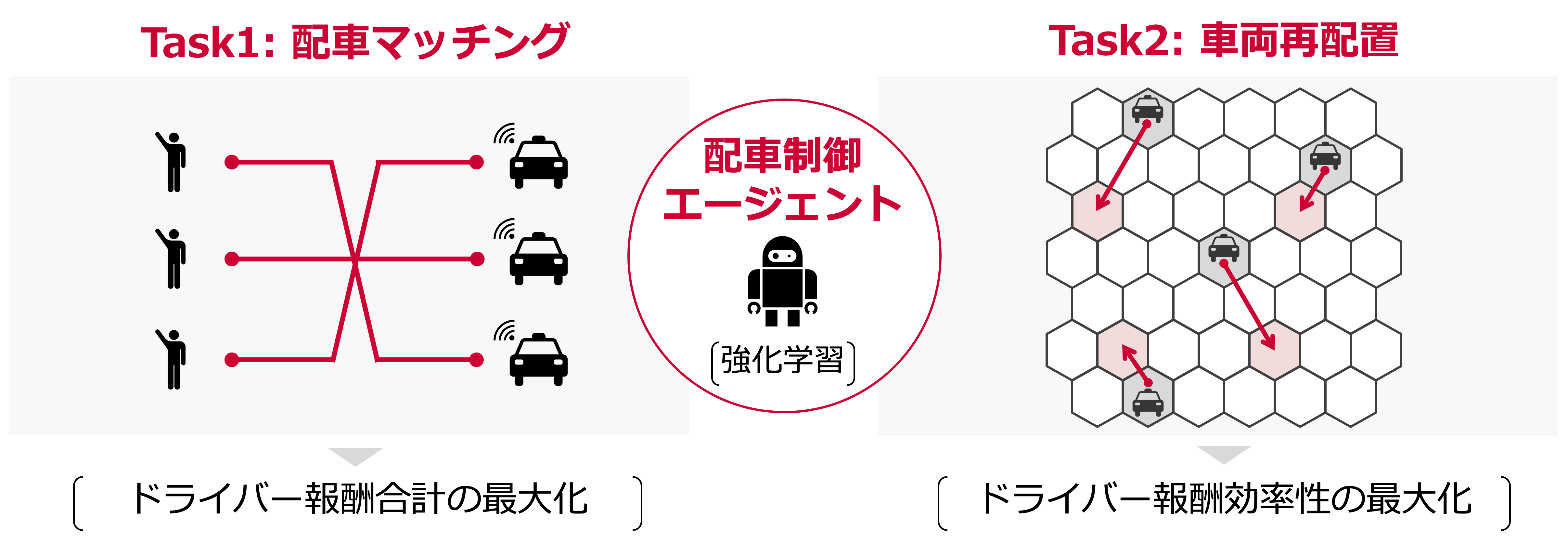
コンペのテーマは**「交通$\times$AI」**で，タクシーの配車割当てや再配置 (Taxi dispatching & repositioning) を最適化するAIの開発でした🚖

Source : [KDD Cup 2020 Reinforcement Learning Competition](https://outreach.didichuxing.com/competition/kddcup2020/)

ドコモR&Dでは，データサイエンス分野の技術力向上を目的に，世界最高峰のデータ分析コンペティションKDD Cupへ毎年参加しています．
2019年は１部門で優勝，続く2020年は３部門で入賞を果たしました1．

受賞したうち機械学習2部門は，以下記事で紹介しています．

そして強化学習部門RL Trackは，世界で1,000チーム以上が参戦し，ドコモR&Dチームが３位を獲得しました．
フルリモートの状況下で，チームメンバの技術を集結した結果です！

本記事では，今回のアプローチや優勝チームの手法解説，強化学習を使う上でのポイントも交え，強化学習の面白さや期待感についても，お伝えしたいと思います！

こんな方におすすめ

  • 機械学習や強化学習をこれから学ぼうとされている方
  • 強化学習を使ったコンペティションに興味がある方
  • ビジネスに強化学習がどのように活用できるか気になる方

本記事の内容

  • 強化学習の概要と機械学習における位置付け
  • タクシー配車制御における強化学習を用いたドコモR&Dチームのアプローチ
  • コンペティションの上位チーム手法や，強化学習の活用方法についての解説

コンペティション概要

今回のお題は，オンデマンド交通におけるタクシー配車を強化学習で最適化するものでした．

「オンデマンド交通」とは，利用者の乗車要望に基づき運行する交通サービスです．
サービス事業側は，車両を適切に配車し，運行効率を向上させることが重要になります．
特に関心の高い，以下の2つの配車タスクが，コンペティションの課題として出題されました．

  • Task 1 : 乗車オーダーとドライバーのマッチング (Order dispatching)
  • Task 2 : タクシー車両の再配置 (Vehicle repositioning)

problem_v2.png

スポンサーは本分野リーディングカンパニーの滴滴出行 (Didi Chuxing)，コンペティションプラットフォームは実績あるBiendata で開催されました．
特に，リアリティがある問題設定やスポンサーからのデータ提供による今回のコンペティションは，個人的に没頭するほど興味深いものでした！

強化学習とは

まずは強化学習の概要から説明し，本コンペティションで強化学習を用いるモチベーションを解説していきます．

概要

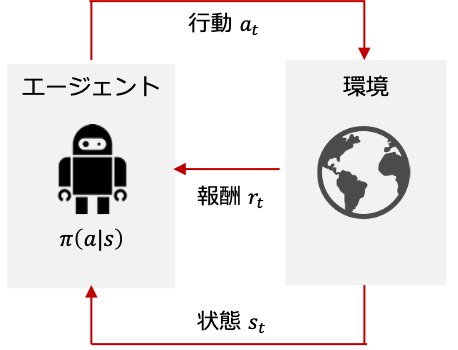
強化学習 (Reinforcement Learning) は，エージェントが試行錯誤を通じて，最適な制御を獲得する機械学習のひとつの手法です．

about_RL.png

強化学習では図にあるマルコフ決定過程 (Markov Decision Process) のように，行動$a_t$，状態$s_t$，報酬$r_t$を伴います．
エージェントは，この報酬を最大化するような方策 $\pi(a_t|s_t)$ や，状態$s_t$で行動$a_t$をとった際の行動価値$Q(a_t, s_t)$を，環境から学習することになります．

バンディットアルゴリズム

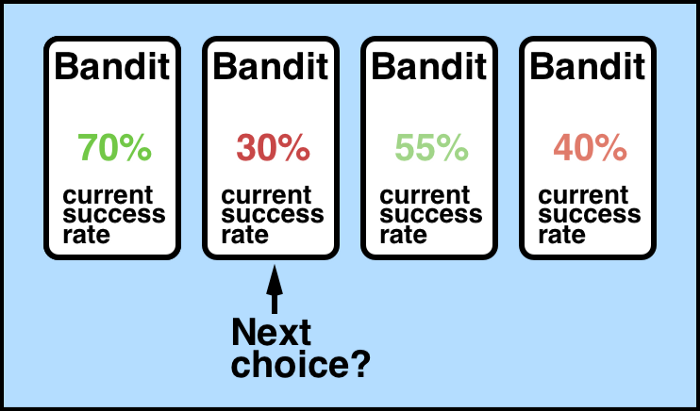
強化学習の特殊なパターンとして，多腕バンディット問題 (Multi-armed Bandit Problem) があります．

about_bandit.png

Source : Solving the Multi-Armed Bandit Problem

複数の候補（例：スロットマシンの台）を腕 (arm) として考え，未知の報酬分布を持つ$K$本の腕を逐次的に選択し，累計報酬を最大化させる問題です．

多腕バンディット問題では，行動$a_t$によって状態$s_t$が変化しないため，よりシンプルな問題設定と言えます．時間発展として考えると，以下の違いがあります．

  • 強化学習：$s_1$, $a_1$, $r_1$, $s_2$, $a_2$, $r_2$, $\dots$
  • 多腕バンディット問題：$a_1$, $r_1$, $a_2$, $r_2$, $\dots$

深層強化学習

次は，強化学習の発展形で，深層学習と組み合わせた深層強化学習 (Deep Reinforcement Learning) が，近年，大きな進歩を見せています．

例えば，行動価値関数（Q関数）に深層学習を適用し，他にも学習の安定化の工夫を施したDQN (Deep Q-Network) があります．

適用事例として有名なものは，Google DeepMindが構築したAlphaGoで，囲碁世界チャンピオンにも勝利しました．
深層強化学習は今や，こうしたゲーム分野だけでなく，システム制御やコンシューマ向けサービスへの活用も進み始めています．
例えば，同じくGoogle DeepMindは，深層強化学習によってデータセンターの冷却電力を40%削減できたと発表しました．

機械学習での位置付け

上記では，強化学習やその周辺を簡単に説明しました．
次は，**教師あり学習，教師なし学習といった他の機械学習とどう違うのか？**という点に触れていきます．

自身の理解の助けとなった，以下の資料を引用して説明すると，最も異なる点はデータの与え方にあります．

  • 教師あり・なし学習では，前提としてデータは所与
  • 一方，強化学習では，環境を探索して主体的にデータを獲得する必要あり

また，学習目的にも以下の違いが見られます．

  • 教師あり学習：完璧な予測
  • 教師なし学習：法則の発見
  • 強化学習：適用行動の獲得

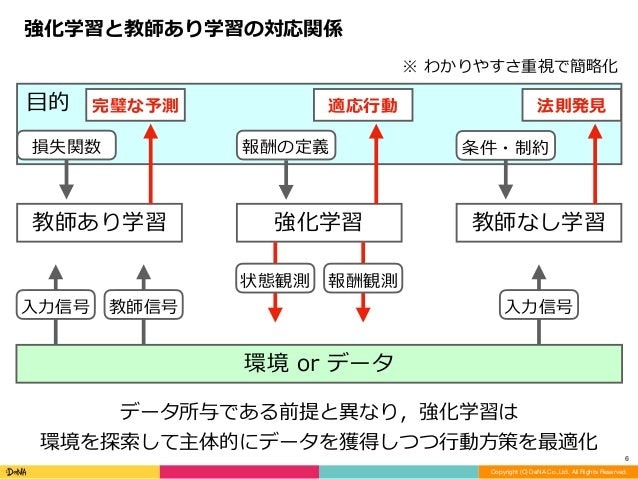
thumbnail
Source : 多様な強化学習の概念と課題認識

なぜ強化学習？

強化学習と他の機械学習との違いを明確にしたところで，本コンペティションで強化学習を使うモチベーションを説明します．

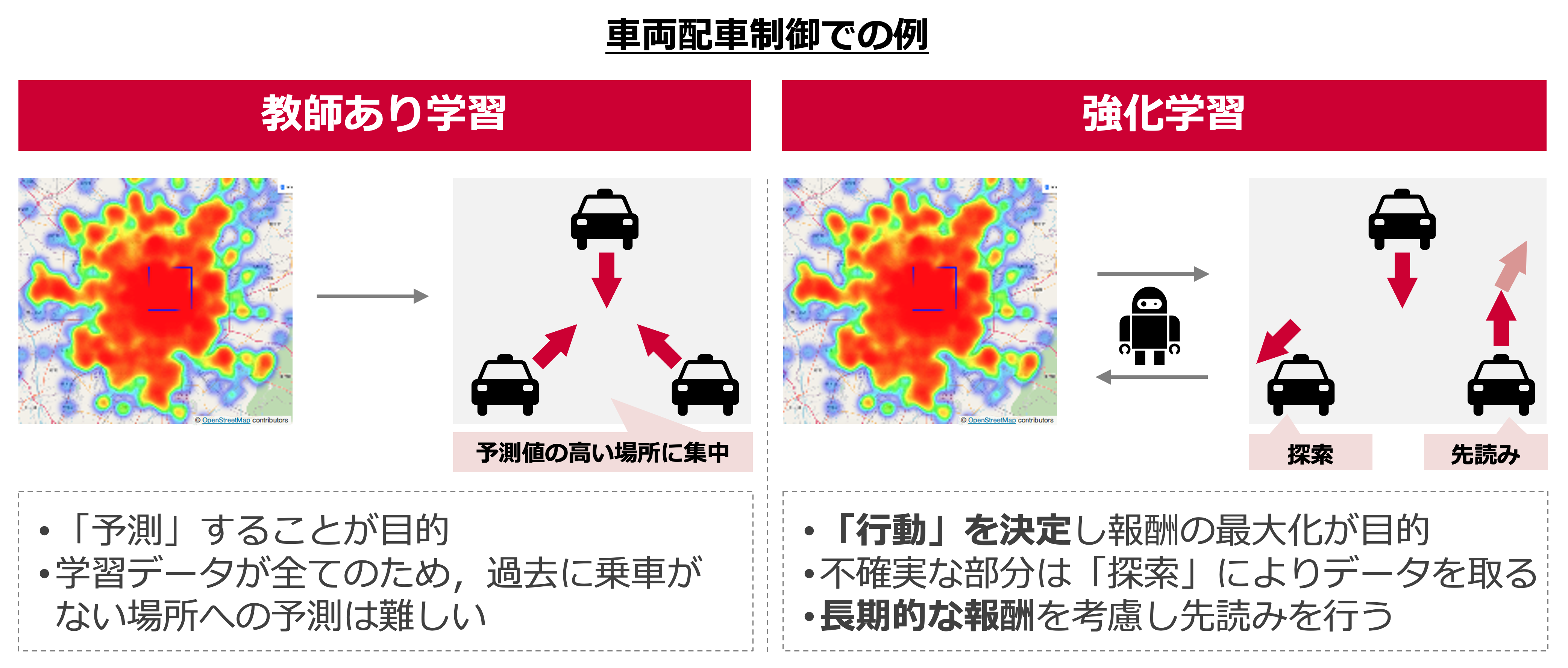
SV_RL_v2.png

タクシー車両の配車制御を考えた場合，「最も需要が集まりそうな場所」を予測する，教師あり学習のアプローチも考えられます．
この場合，所与でデータが大量にあれば高精度に需要を予測できますが，過去に乗車がない場所の予測は難しいと考えられます．

一方，「配車を通じて得られる報酬の最大化」を目的とした，強化学習のアプローチでは，

  • この様な需要が不確実な乗車ポイント（過去に配車していない）も「探索」によりデータを取って判断する
  • 更に，長期的な報酬を加味して，（先読みのような形で）人が思いつかないような配車パターンを獲得する

といったメリットが期待できます．ただし，これらを享受するには，報酬の定義や（マルコフ決定過程における）状態の与え方を適切におこなう必要があります．

こうした背景から，タクシーの配車制御（Order dispatching, Vehicle repositioning）の強化学習アプローチが，DiDi AI Labをはじめ近年，盛んに提案されています．

コンペティション詳細

ここからは，今回の強化学習コンペティションの詳細を説明していきます！

タスク

コンペ概要で触れたように，今回，2つのタスクOrder DispatchingとVehicle Repositioningが出題され，エージェントの性能はそれぞれの指標で評価されます．

  • Task 1 : Order Dispatching

    • 制御内容：乗車リクエストにたいして，配車すべき車両のマッチングを決定（時間ウィンドウは2秒間）
    • 評価方法：ドライバーの平均総利得の最大化

  • Task 2 : Vehicle Repositioning

    • 制御内容：空車状態の複数車両について，各々の再配置ポイントを決定（5分以上の空車車両が対象）
    • 評価方法：ドライバーの報酬効率性の最大化

また，前提として**「強化学習の手法を用いることが推奨される」とコンペティションルールに記載**されていました．

コンペの難しさ

今回はコードコンペティションで，Order dispatchingとVehicle repositioningのそれぞれのクラス(Dispatcher, Repositioner)を記述し，pythonコードを提出する方式でした．

以下に今回のコンペティションの難しさをまとめます．

  1. タスク同士の依存関係

    • 乗車マッチングと再配置の各アクションは影響し合うはず
    • 双方のアルゴリズムを実装して，コードをサブミットする

  2. 公式なシミュレータは未提供

    • 過去実績のデータが与えられるのみ
    • サブミット時の詳細ログは残らない（スコアのみ開示）

  3. ダイナミクスにおける情報量の少なさ

    • 車両の細かな挙動条件が明かされていない部分がある

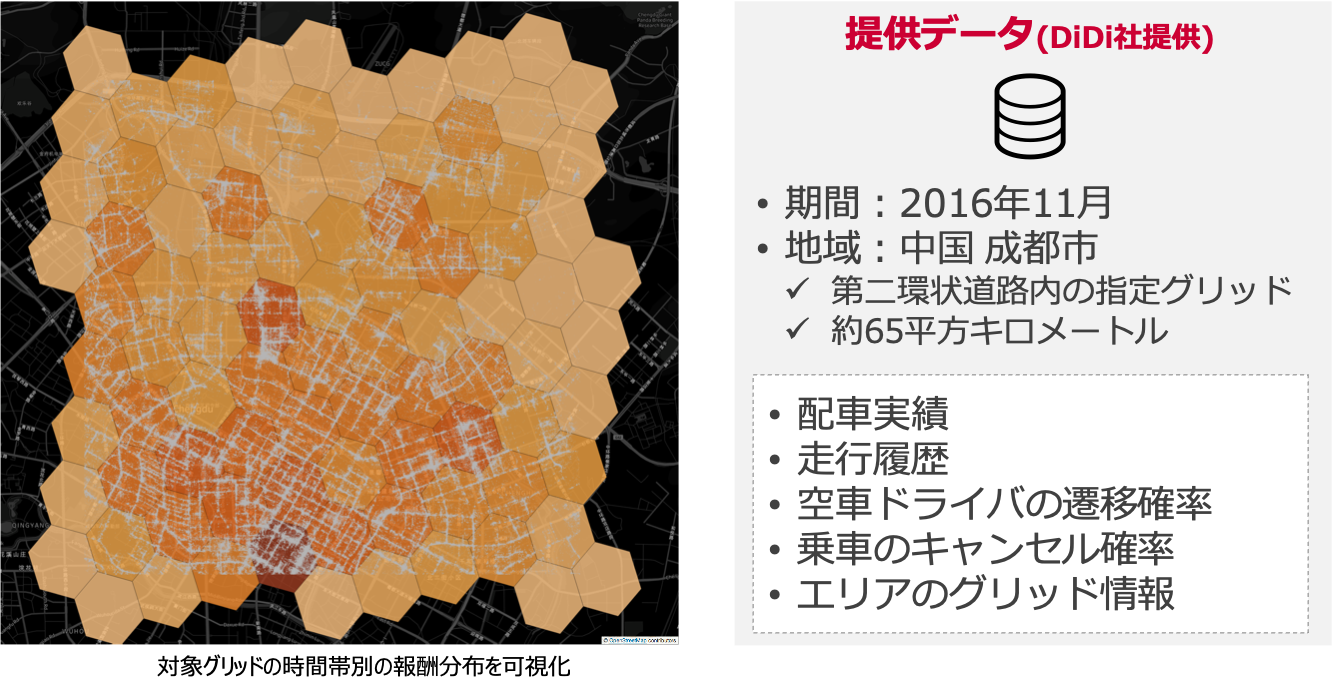
提供データ

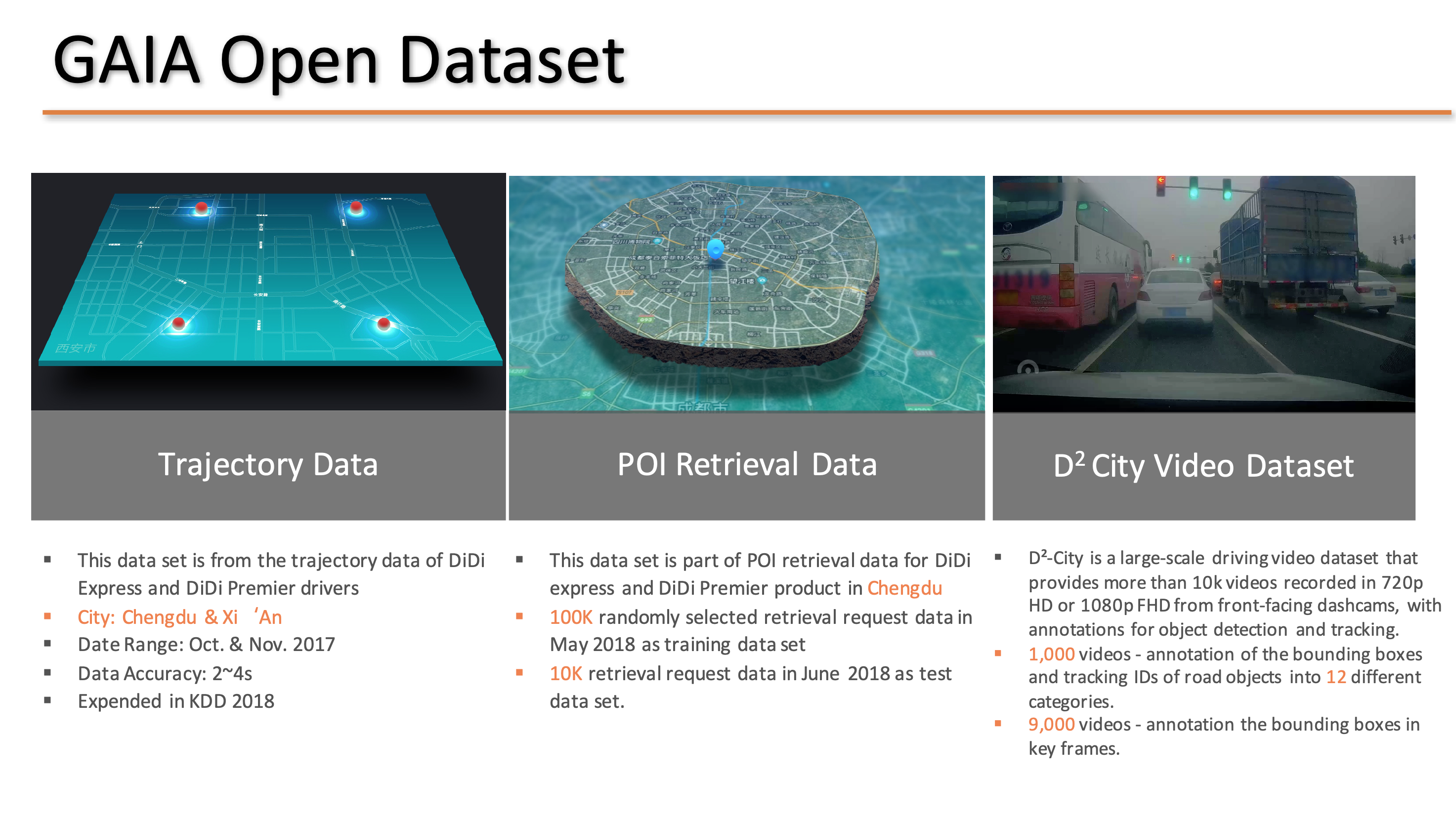
gaia.png
Source : [Deep Reinforcement Learning with Applications in Transportation, KDD2019 Tutorial] (https://outreach.didichuxing.com/internationalconference/kdd2019/tutorial/DRL-with-Applications-in-Transportation_KDD19tut_20190729.pdf)

Didi Chuxingが公開しているGAIA Open Dataset上で，コンペ参加者向けに過去の配車・走行に関するデータセットが提供されました．

  • データ対象
    • 期間：2016年11月分
    • 場所：中国 成都市エリア
  • データ種類
    • 配車実績
    • 走行履歴
    • 空車ドライバの遷移確率
    • 乗車のキャンセル確率
    • エリアのグリッド情報

ある時間帯でのグリッド別の報酬分布を可視化した例を以下に示します．

コンペティションで対象とされるグリッド範囲は，約65平方キロメートルのエリアとなります．

about_Data.png

アプローチ

では，私たちNTT DOCOMO LABSチームの手法紹介に入ります．

サマリー

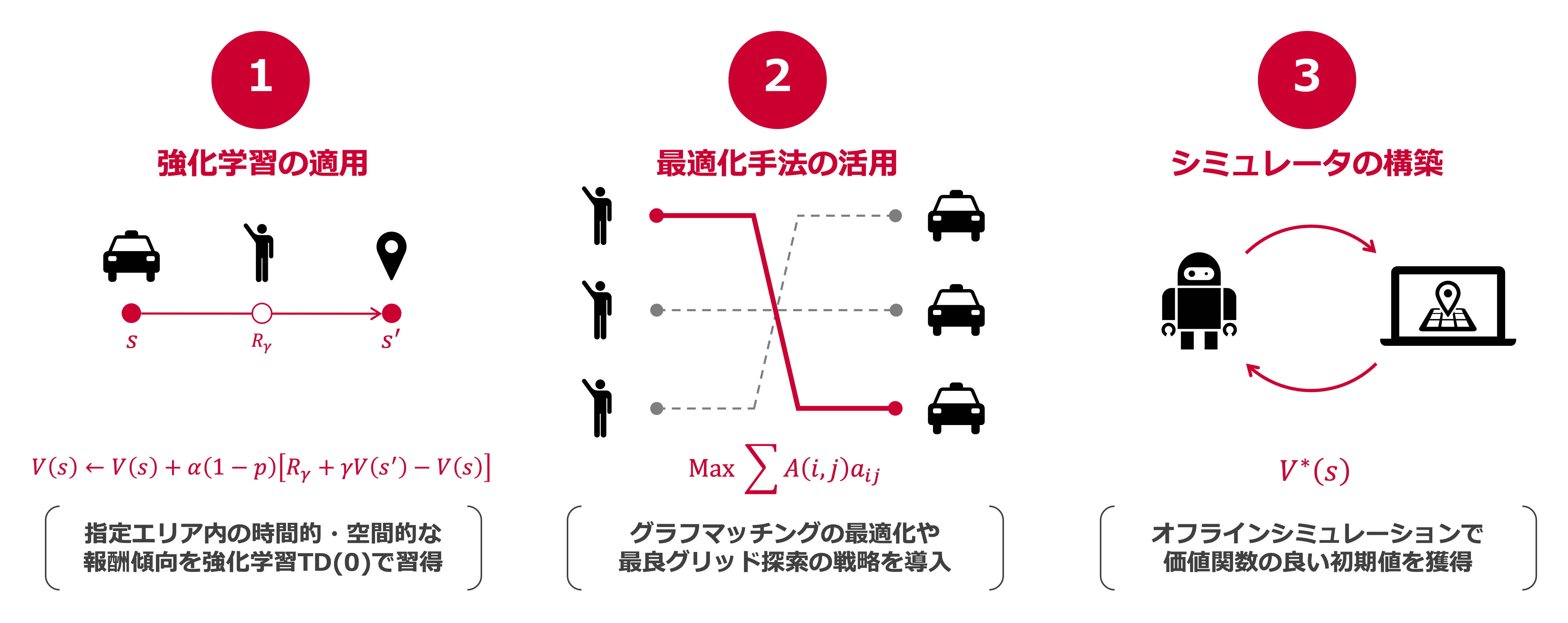
私たちは，サブミット環境の情報が未知である点に留意して，なるべくシンプルで学習を安定化させつつ，高報酬を獲得するエージェントの構築を目指しました．

そのための主な工夫点は，以下の３つです．

  1. 時空間の報酬傾向を価値関数に反映し，TD(0)で学習
  2. グラフマッチングやグリッド探索に最適化手法を活用
  3. オフラインでのシミュレータを実装し，良好な初期値を獲得

approach_v2.png

順に各ポイントを解説していきます．

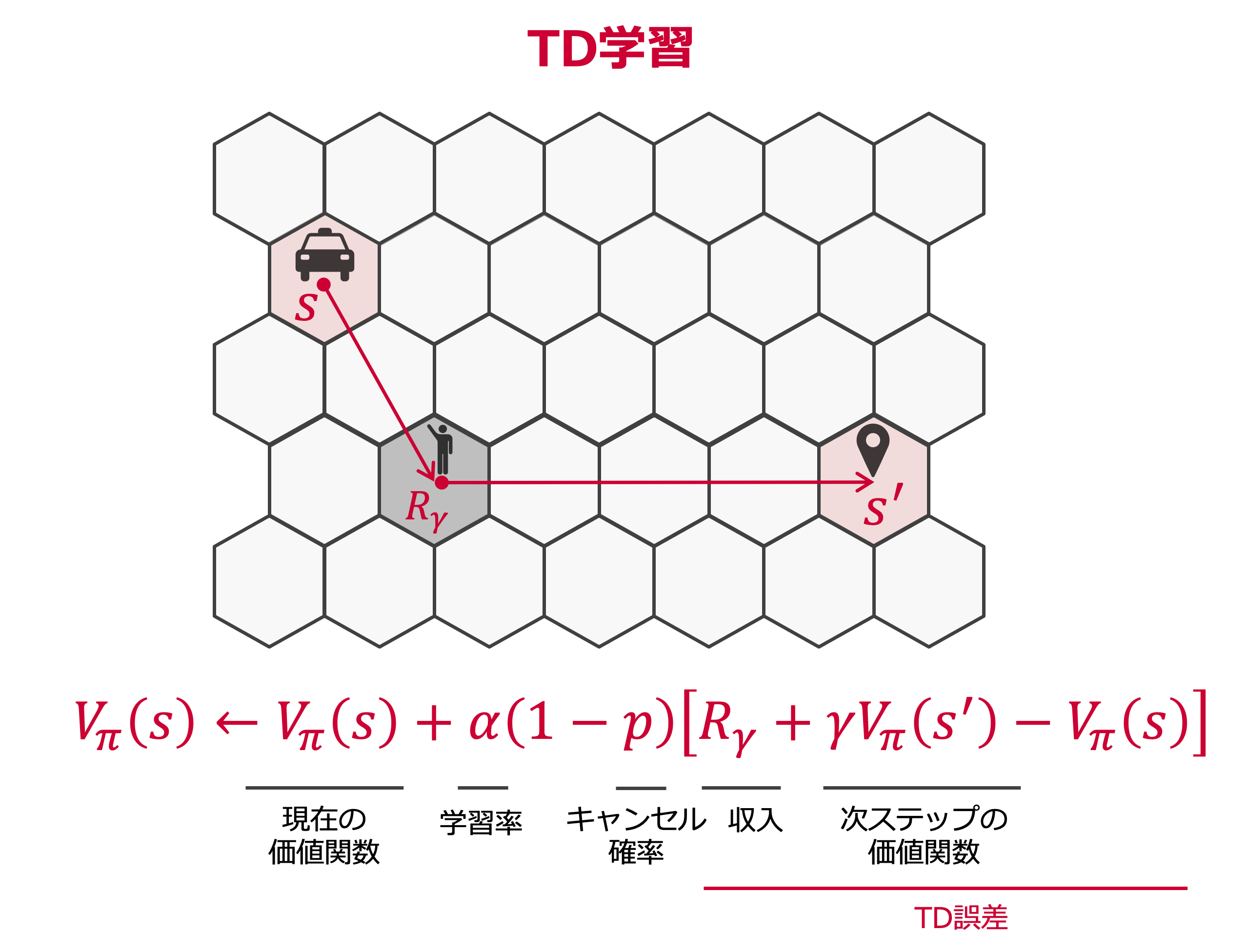
価値関数の学習

まず，強化学習のアプローチをとる上での，モデリングについてです．

私たちは各車両を（区別せずに）単一のエージェントとみなし，マルコフ決定過程を以下で定義しました．

  • 時間ステップ：離散時間（2秒間の時間ウィンドウ）
  • 状態：ドライバーの時空間的な情報（グリッドID,時間インデックス）
  • 行動：乗車またはアイドル状態
  • 報酬：乗車料金
  • 状態価値：各状態における収入期待値

approach_TD0_2.png

このように定義したもとで，状態価値の更新は，KDD2018の論文2を参考にTD学習 (Temporal Difference Learning) を採用しました．
$$ V_\pi (s) \leftarrow V_\pi (s) + \alpha(1-p) [R_\gamma + \gamma V_\pi (s')-V_\pi (s)]$$

approach_TD0_1.png

Order Dispatching

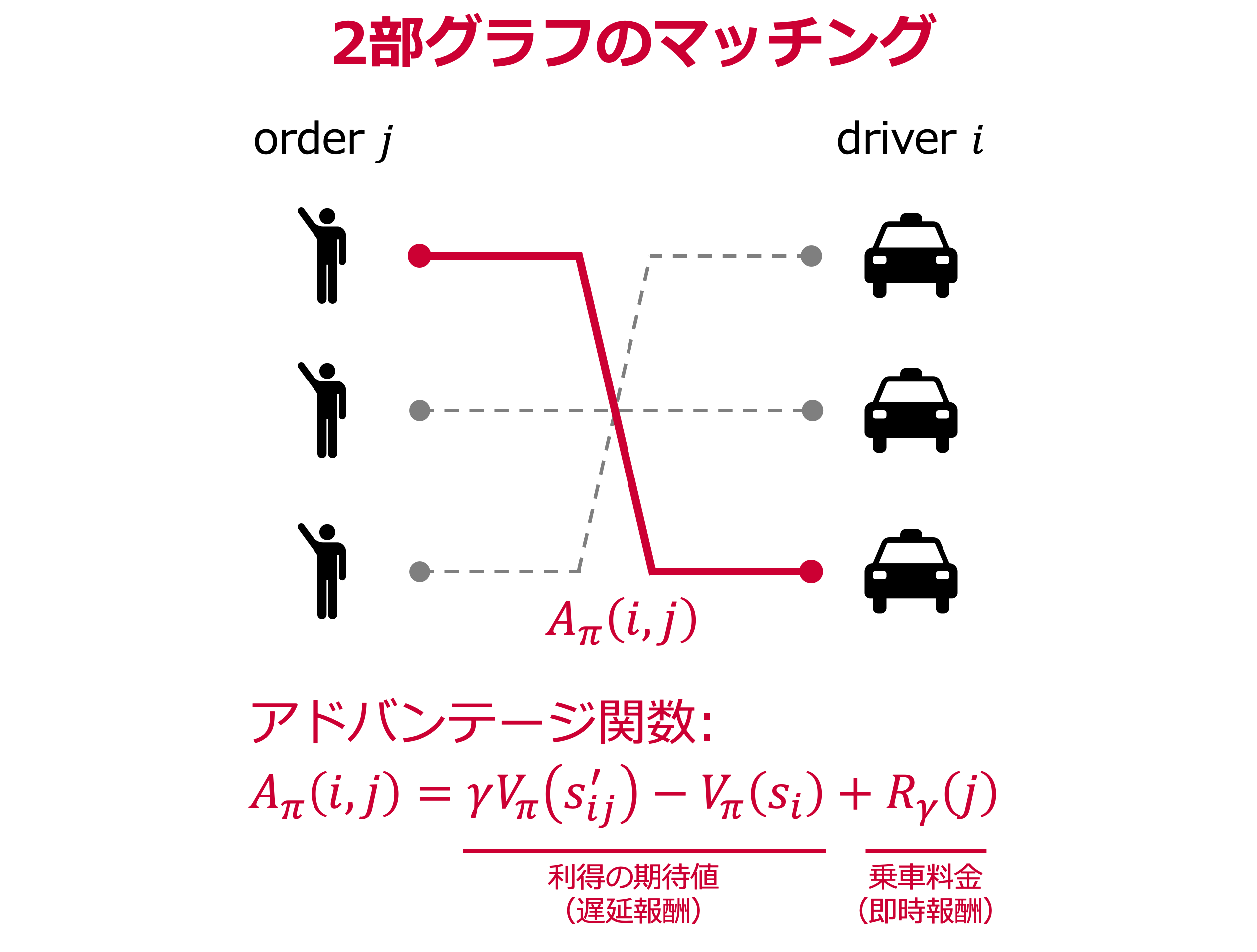
時空間的な状態価値を定義し，学習則を与えた次は，各タスクのプランニングについて考えます．

まず，乗車オーダーとドライバーのマッチングであるOrder Dispatchingは，先ほどのKDD2018の論文2のアプローチを取り入れています．

まず，将来の利得分も考慮した乗車割当てを2部グラフで表現する際に，以下のアドバンテージ関数を用いました．

$$ A_\pi (i,j) = \gamma V_\pi (s'_{ij})-V_\pi (s_i) + R_\gamma(j) $$

approach_dispatch_1.png

このマッチングを組合せ最適化問題として定式化すると以下になります．
この最適化では，ハンガリアン法(Kuhn-Munkres algorithm)3を用いることで，高速な求解を目指しました．
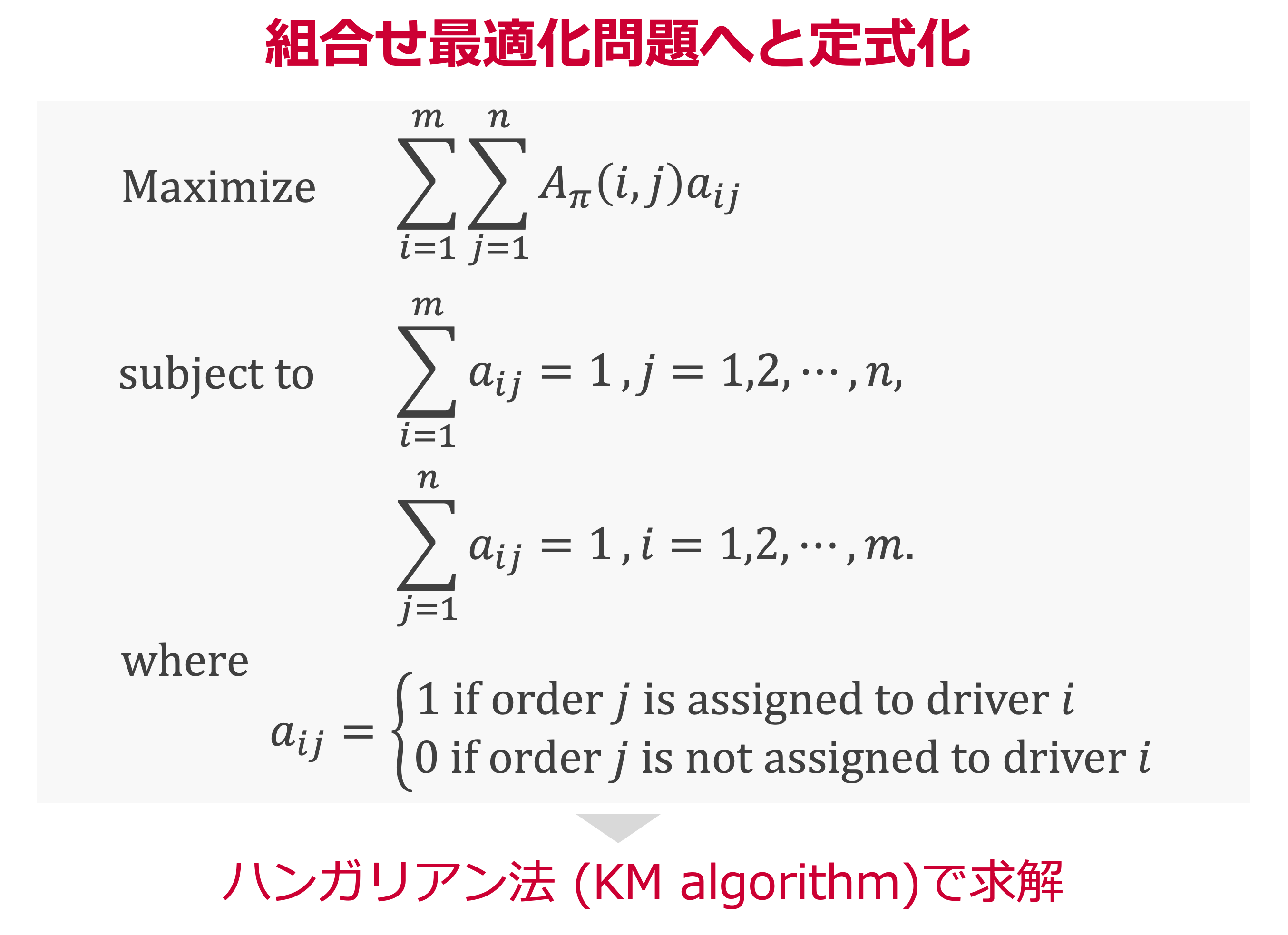
approach_dispatch_2.png

実装例 : KM algorithm

ハンガリアン法を使った実際の導出は，scipy.optimizeのlinear_sum_assignmentを利用しています．

たとえば，ドライバー3台，乗車オーダーが3件で以下のアドバンテージ関数が得られた状況の実装例を示します．

A_{\pi}(i,j)=
\begin{bmatrix}
4 & 1 & 3 \\
2 & 0 & 5 \\
3 & 2 & 2
\end{bmatrix}

import numpy as np
from scipy.optimize import linear_sum_assignment

driver_id = ['d_1', 'd_2', 'd_3'] # ドライバーID
order_id  = ['o_1', 'o_2', 'o_3'] # オーダーID

# アドバンテージ関数
adv = np.array([[4, 1, 3], [2, 0, 5], [3, 2, 2]])

# ハンガリアン法（KM algorithm）の実行
row_ind, col_ind = linear_sum_assignment(adv, maximize=True)
driver_order_idx = list(zip(row_ind,col_ind))

# マッチング結果を出力
matching = \
list(map(lambda idx : {"driver_id" : driver_id[idx[0]],
                       "order_id"  : order_id[idx[1]],
                       "score"     : adv[idx[0],idx[1]]},
         driver_order_idx))

print(matching)

こちらの出力は以下で，マッチングによる報酬スコア合計は11となります．

[{'driver_id': 'd_1', 'order_id': 'o_1', 'score': 4},
 {'driver_id': 'd_2', 'order_id': 'o_3', 'score': 5},
 {'driver_id': 'd_3', 'order_id': 'o_2', 'score': 2}]

論文紹介資料

今回のアプローチである，TD学習やハンガリアン法をOrder dispatchingに適用する部分は，KDD2018の論文2を参考に実施しました．

また，この論文を含むOrder dispatchingやRepositioningの紹介資料として，以下の2つ資料が非常に参考になりました！
thumbnail
Source : タクシー配車アルゴリズムへの強化学習活用：Reinforcement Learning Application

thumbnail
Source : KDD2018 DiDi "large-scale order dispatch in on-demand ride-hailing platforms: a learning and planning approach"

Vehicle Repositioning

次に，空車状態の車両再配置のプランニングについてです．

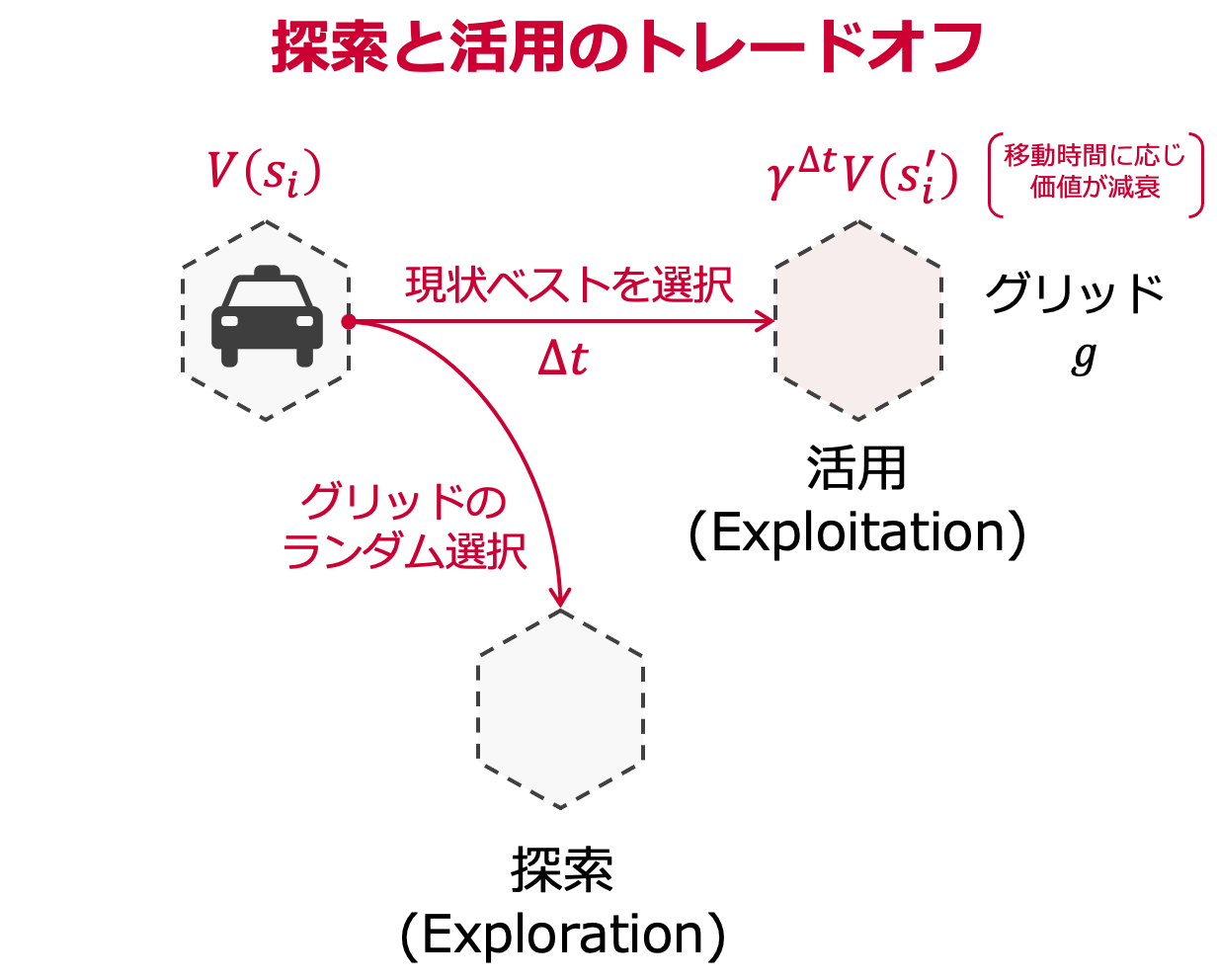
ここでも，状態価値関数を利用するのですが，グリッド探索を行うために，$\varepsilon$-Greedy algorithmを試しました．

  • 活用：（グリッドまでの移動時間$\Delta t$を考慮した）現状ベストの状態価値をもつグリッドを選択
  • 探索：（各グリッドの報酬傾向を得るために）移動先のグリッドをランダムに選択

approach_reposition_2.png

パラメータ$\varepsilon$によって，ランダム性を制御しています．
サブミットやオフライン検証を通じて，最終的にはperfect greedy ($\varepsilon=0$)なエージェントで実行しました．

approach_reposition_3.png

シミュレータ

本コンペでは，過去データとサブミット環境（各ステップの報酬や状態の履歴は残らない）のみが与えられていました．

そのため，エージェントの学習状態を適切に把握するために，自分たちで配車制御のシミュレータを構築する必要がありました．
私たちは，過去データを用いオフライン環境で学習させるアプローチをとり，得られた状態価値$V^{*}_{\pi}(s)$をサブミット時の良好な初期値として活用しました．

approach_simulator_1.png

コンペ結果

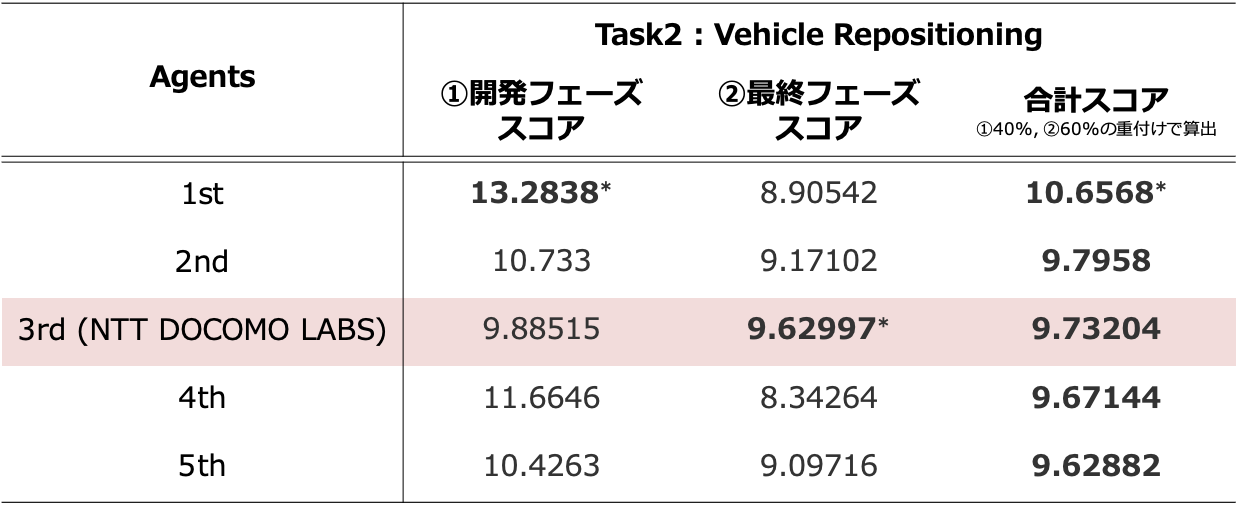
Task1, Task2ともに開発フェーズの上位25チームが，最終フェーズに残り，各フェーズの重付けスコアで，コンペティション順位が決定されました．

私たちNTT DOCOMO LABSは，Task2 (Vehicel Repositioning)で開発フェーズを通過し，最終フェーズでは全チーム中の最高スコアを獲得しました．

最終順位は重み付けスコアにより3位となりましたが，
開発フェーズ，最終フェーズでも安定して高スコアが出せていた点は，オフライン環境でのシミュレーションや良い初期値を獲得したことによるものと考えられます．

result.png

他の手法紹介

Dispatch : 1位チームの手法

Task1の優勝チームPolar Bear（Beihang University, 4Paradigm Inc.）の手法は以下の通りです．

  • エージェントの学習とプランニングは，同じくTD学習，KMアルゴリズムを利用
  • 2部グラフのマッチングは，K近傍グリッドのみに限定して高速化
  • 状態価値を，単一グリッドでなく周辺グリッドも考慮したCoarse codingで表現(X.Tang et al. KDD20194のアプローチ)

KDD2019.png

Source : A Deep Value-network Based Approach for Multi-Driver Order Dispatching, KDD 2019

Reposition : 1位チームの手法

Task2の優勝チームTLab (Purdue University, Southeast University)の手法は以下の通りです．

  • Globalなエージェントが，全車両を同時に制御するアプローチ
  • 状態もGlobalとLocalの2種類を導入し，グリッドの解像度はN＝30程度に限定
  • 方策ネットワークには，Double Deep Q-Learning5を採用
  • 自前のシミュレータは，Juliaで実装（Python実装版に比べて10倍の高速化に成功）

非常に特徴的な手法や，実装面での工夫がなされていて，参考になりました．
特に，Globalなエージェントを導入することで，ドライバー同士の需要の取り合いなども解消されると考えられます．
また，オフライン環境におけるシミュレータの高速化は，私たちのチームでも課題となっていました．
python実装をJuliaに書き換えて，10倍の高速化をされたのは本当にすごいと思いました．
（これを機に，本格的にJuliaを学んでいこうと思います！）

教師あり学習との比較

ここまでは強化学習ありきで説明してきましたが，モチベーションでも触れたように，

「Task2のVehicle Repositionは，過去データを基にした教師あり学習でどの程度の精度が出るか？🤔」

という疑問がありました．
そこで，コンペティションの序盤では，教師あり学習でグリッド別の乗車需要を予測し貪欲法で再配置を決定するルールベースのアプローチも検討していました．

コンペティションで与えられた過去データを基に，現在時刻から$T$分先（$T=10,20,\dots, 60$）の各グリッドのRewardを予測するモデルを，LightGBMで作成し，サブミットしました．　

アプローチ 開発フェーズスコア
強化学習(TD Learning) 9.62997
教師あり学習(LightGBM)+貪欲法 8.62987

今回の過去データセットとサブミット環境での結果一例ではありますが，強化学習の性能の良さに驚きました！

検討手法と振り返り

今回のコンペティションでは，モデルフリーの強化学習を利用しましたが，（学習済みの）需要予測モデルを活用したモデルベースのアプローチも検討していました．

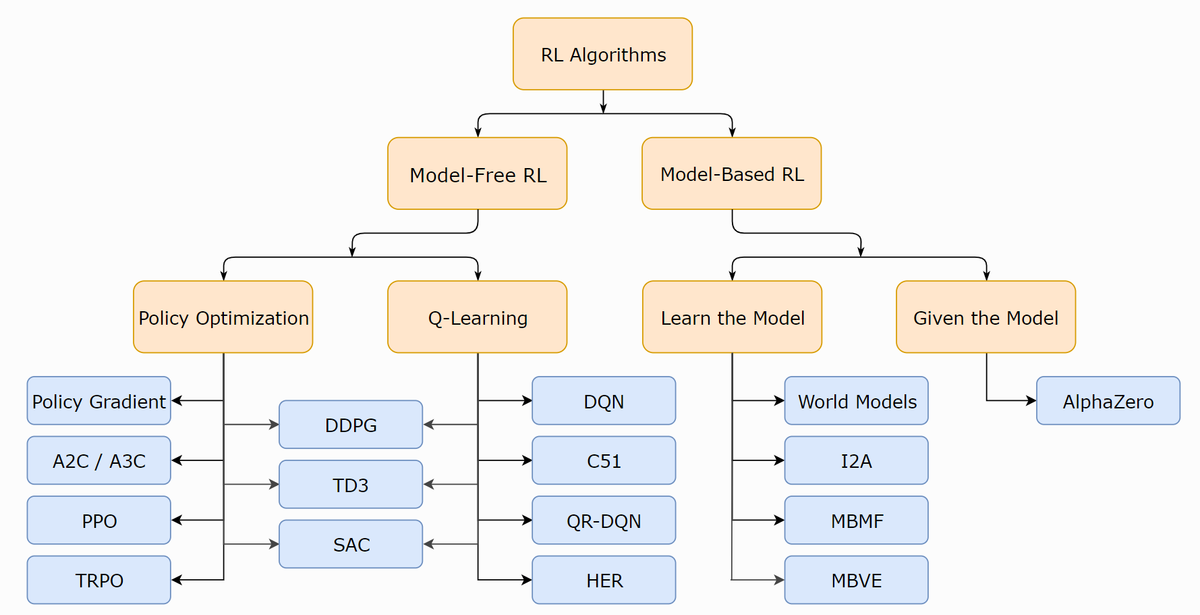
rl_algorithms_9_15.png
Source : A Taxonomy of RL Algorithms, Open AI Spinning Up

モデルベースの強化学習では，サンプル効率が良いとされており，本コンペティションでも学習収束が速まることを期待して実装を進めましたが，サブミット時の計算時間の打ち切り制限に引っかかる等で，コンペ期限内での評価はできませんでした．

コンペ全般で言えることですが，試したい手法を早期に洗いざらいリストアップし，計画的に分担・進行させることが何よりも重要だと感じました．

しかし今回，約3ヶ月といったコンペ期間で，フルリモートの状況下で社内部署の垣根を超え，以下をチームメンバで集結できた経験は，とても貴重なものでした！

report.png

  • 交通分野のドメイン知識に基づく戦略立て
  • 最先端の強化学習手法のサーベイと活用検討
  • 既存データセットを元にした予測モデルの検証
  • 未知環境を考慮した強化学習と最適化手法の実装
  • オフライン環境の配車制御シミュレータの構築
  • マシン環境，データベース整備やコード管理
  • リーダーボード監視・通知に基づく方針修正

強化学習コンペティションの紹介

強化学習を使ったコンペティションにご興味をもたれた方に，今回以外の情報を以下でリストアップしています．

また，今回のKDD Cup 2020 RL Trackは，コンペ終了後もPost-Competition Submissionとして，Order Dispatching (Task 1)やVehicle Repositioning (Task 2) の評価が可能な状態になっています．

両タスクとも，開発フェーズと最終フェーズのどちらの環境でもサブミットできますので，汎用的なエージェントが学習できているかを確認することも可能です．

強化学習のビジネス活用：広告配信の最適化

ここでは，ビジネスで強化学習のアプローチがどのように使われているか，簡単にご紹介します．

ビジネスにおいて，最適な行動選択を求められる機会は多くあります．
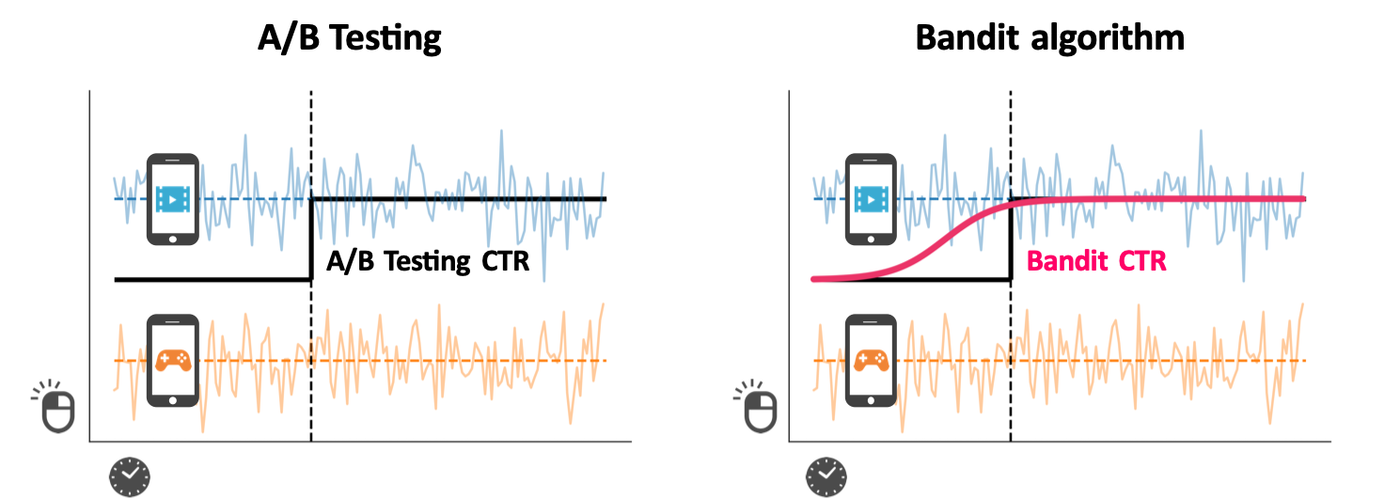
例えば，Web広告の配信を考えた場合，複数の広告の中から最適なものを選び，ユーザに表示させたいというものです．なるべくクリック率（CTR）が高いものを選択し，累計クリック数を増やすことが可能ですが，CTRは試行させてみるまでは分かりません．

こうした場合に，バンディットアルゴリズムを適用することができます．

ab_test.png

一般的なA/Bテストでは，検証をすることで最適な選択は可能ですが，検証している間に効果が低いものも同じ分だけ選択するため，ロスが生じてしまいます．

これに対しバンディットアルゴリズムでは，一定期間内で報酬を最大化させるため，トレードオフの関係にある次の２つの戦略を織り交ぜながら，学習を進めていきます．

  • 探索（exploration）: 候補の期待報酬についての情報を獲得する
  • 活用（exploitation）: 獲得した情報を使いより良い候補を選択する

さらに，ユーザ情報といったコンテキストを考慮して，広告配信のパーソナライズ（ユーザ毎の広告出し分け）に取り組んだ事例を以下記事に解説しています．

バンディットアルゴリズムによる広告配信の最適化【基礎と実践】

さいごに

本記事では，強化学習を中心にした学習体系や，コンペティションの事例について紹介しました．
今回のKDD Cup 2020 RL Trackのアプローチについては，以下でスライドを公開しております．

thumbnail
Source : KDD Cup 2020 RL Track : Learning to Dispatch and Reposition Competition 3rd Place Solution

また，昨年のKDD2019 tutorialのDeep Reinforcement Learning with Applications in Transportationでは，DiDi AI Labによる重厚なTutorial資料が公開されました．
強化学習の基礎から，交通分野における強化学習の最先端手法まで広くまとめられており，非常にオススメでです！

Source : [Deep Reinforcement Learning with Applications in Transportation, KDD2019 Tutorial] (https://outreach.didichuxing.com/internationalconference/kdd2019/tutorial/DRL-with-Applications-in-Transportation_KDD19tut_20190729.pdf)

今回の記事が，強化学習に触れる上での皆さまの一助となれば幸いです！

これからも最先端のAI・ビッグデータ分析技術を強化し，新しい価値や感動を提供し続けることができるよう，取り組んでまいります．

それでは良いお年を🎍

  1. NTT DOCOMOテクニカル・ジャーナル Vol. 28 No. 3 : [pdf] ↩

  2. Xu, Zhe, et al. "Large-scale order dispatch in on-demand ride-hailing platforms: A learning and planning approach." KDD2018. ↩ ↩2 ↩3

  3. Munkres, James. "Algorithms for the assignment and transportation problems." Journal of the society for industrial and applied mathematics, 1957. ↩

  4. Tang, Xiaocheng, et al. "A deep value-network based approach for multi-driver order dispatching." KDD2019. ↩

  5. van Hasselt, Hado, Arthur Guez, and David Silver. "Deep Reinforcement Learning with Double Q-Learning." AAAI2016. ↩

88
63
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
88
63

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?