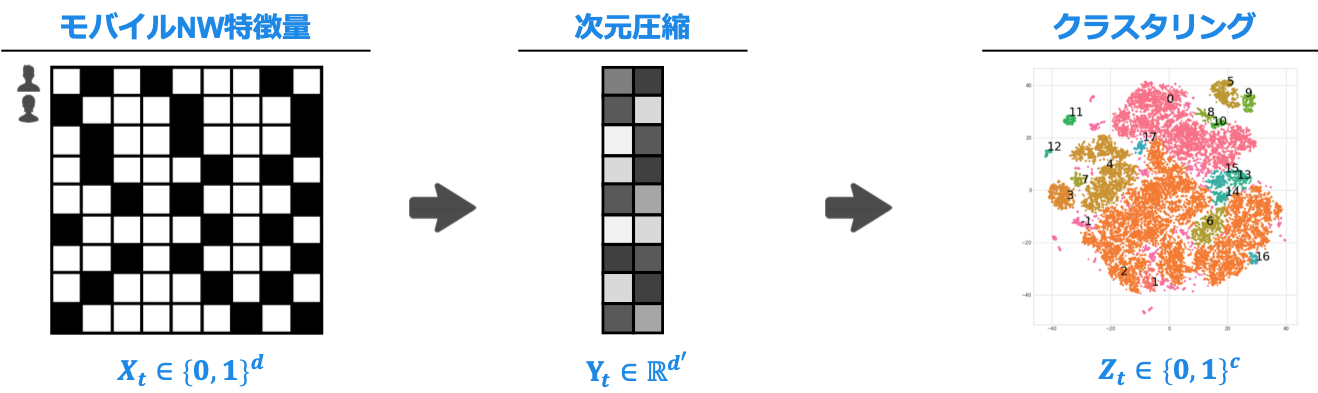バンディットアルゴリズムによる広告配信の最適化【基礎と実践】

こんにちは，NTTドコモの出水です。
私は業務で，マーケティング分野を中心に社内外のデータ解析や社会システムの最適化に取り組んでいます。

本記事では，Bandit algorithmに焦点を当てて，アルゴリズムの基礎的な解説や，実システムへ広く適用するための手法例について述べます。
また，最後にpythonでのサンプルコードも載せています。

Bandit algorithmとは

ビジネスにおいて最適な選択を求められる機会は多くあります。例えば，Web広告の配信 を考えた場合，複数の広告クリエイティブの中から最適なものを選び，アクセスユーザに表示させたいというものです。なるべく クリック率（CTR） が高いものを選択することで，累計クリック数を増やすことが可能ですが，CTRは試行させてみるまでは分かりません。

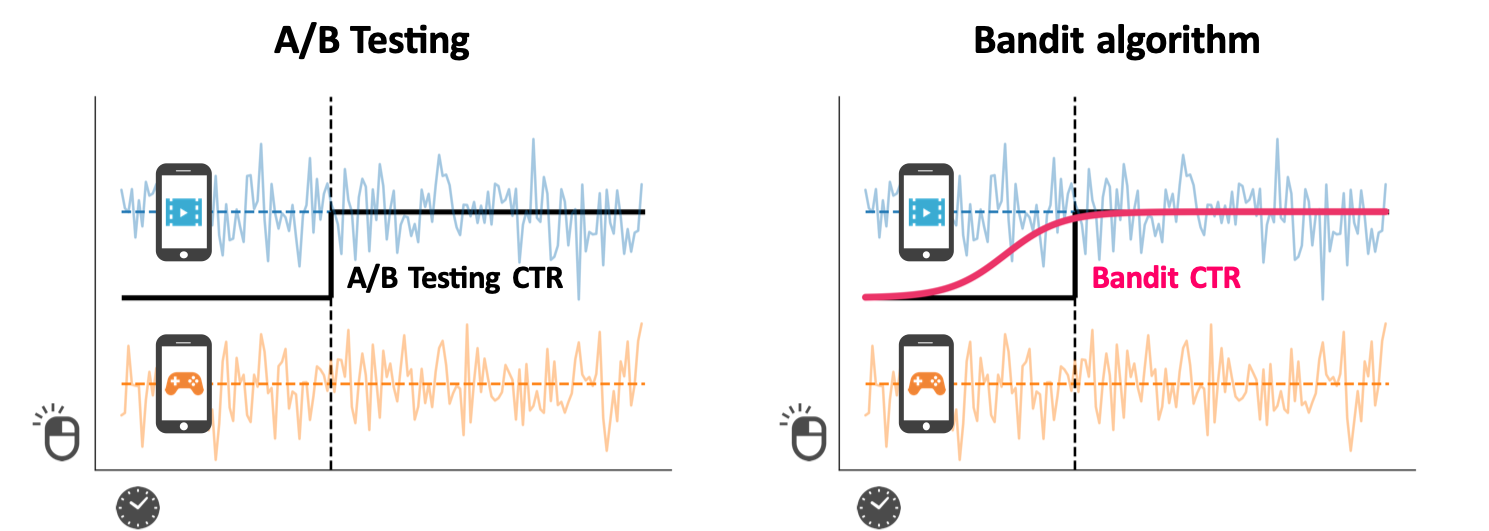
一般的に用いられる手法として，A/Bテスト があります。図にあるように，2つの広告クリエイティブの場合，アクセスユーザをランダムに振り分けてCTRを検証した後に，より高い方を採用します。このように，検証をすることで最適な選択は可能ですが，検証している間に効果が低いものも同じ分だけ選択するため，ロスが生じてしまいます。

これに対しBandit algorithmでは，累計の報酬（クリック数など）を最大化させることが目的です。一定期間内で報酬を最大化させるため，トレードオフの関係にある次の２つの戦略を組み合わせていきます。

• 探索（exploration）: 候補の期待報酬についての情報を獲得する
• 利用（exploitation）: 獲得した情報を使いより良い候補を選択する

これらの戦略を柔軟に取り込むことで，図のようにA/Bテストに比べて，より良い結果が見込めます。

アルゴリズムについて

強化学習における位置付け

例に挙げたWeb広告配信のような問題は，多腕バンディット問題（Multi-armed Bandit problem; MAB） と呼ばれています。一つひとつの候補を腕（arm）として考え，未知の報酬分布を持つ$K$本の腕を逐次的に選択し，その累計報酬を最大化することが目的です。

多腕バンディット問題は，強化学習（Reinforcement Learning） の一部として考えることができます。
強化学習では図にあるマルコフ決定過程（Markov Decision Process）のように，行動$A_t$，状態$S_t$，報酬$R_t$を伴います。しかし，多腕バンディット問題では，行動$A_t$によって状態$S_t$が変化しないため，よりシンプルな問題設定と言えます。時間発展として考えると，以下のようになります。

• 強化学習 : $S_1, A_1, R_1, S_2, A_2, R_2, \dots$
• 多腕バンディット問題 : $A_1, R_1, A_2, R_2, \dots$

このように，多腕バンディット問題は，シンプルな問題設定ですが，先ほど述べた様に探索と利用のトレードオフは存在するため，様々なアプローチが考えれられています。代表的なアルゴリズムとして，$\epsilon$-Greedy, Softmax, UCBやThompson Sampling 等が挙げられます。

コンテキスト拡張

再びWeb広告の例に戻って，問題を深掘りしたいと思います。先ほどの例では，アクセスユーザ全体にたいしてCTRが高い広告クリエイティブを見出そうとしていました。しかし，実際にはユーザの層によって，効果の高いものは変わってくるはずです。すなわち，図で示すようにユーザ等の特徴量（Context） を考慮して，それに応じた報酬分布を仮定します。

このように，それぞれのユーザにマッチした広告クリエイティブを選択することで，さらに報酬を増やすことを目指します。特に，特徴量を用いない（Context-freeな）アルゴリズムにたいして，特徴量を考慮したものをContextual Banditと呼びます。

Contextual Bandit

アルゴリズムのおおまかな流れを以下に示します。Contextual Banditでは，ユーザ等の特徴量$X_t$を観測した上で，取るべき行動$a_t$を決定します。その際の報酬$r_t$を受け取った後，報酬分布に関するモデルのパラメータを更新していきます。特に，線形モデルを仮定してUCBを拡張した LinUCB ¹や，同じくThompson Samplingを拡張した LinTS ²があります。

モバイルネットワーク特徴量の活用

ここでは，実サービスにContextual Banditを適用する際，提案した手法³とその効果について述べます。

問題設定

キャンペーンサイトにおけるランディングページ最適化 を目的に，広告プラットフォームへのContextual Bandit適用を目指しました。図のように，アクセスユーザにたいしてランディングページを出し分けることで，累計のコンバージョン数を増やすことが見込めます。

その際に，どのような特徴量を利用するか は重要なポイントです。サービスによっては，詳細なユーザ属性や利用ログといった豊富な特徴量が常に取得できているとは限りません。また，こうした explicitな特徴量 を新たに取得することは，開発コストの増加やプライバシーポリシーの変更等の理由で容易ではありません。

一方で，端末情報や通信情報といった implicitな特徴量 は，獲得コストも低く，加えて，どのようなモバイルサービス上においても共通して利用できることが多いです。ただし，広告クリエイティブのクリックやコンバージョンとの相関は明確ではありません。

そこで，このimplicitな特徴量である モバイルネットワーク特徴量 を活用し，Contextual Banditを広く利用できるようにする手法を考えました。

モバイルネットワーク特徴量

ユーザがモバイルサイトへアクセスした際に取得できる情報で，サイトの種類に依存せず，容易にデータ取得することができます。これらは カテゴリカル変数 である場合が多く，One-hot encoding によりバイナリーベクトルとして表現することが可能です。

しかし，これらの特徴量は，非常に多くのカテゴリーが存在するため，特徴量ベクトルの次元数は膨大です。このままの状態でContextual Banditにかけると，スパース性の問題 や 計算負荷の問題 が発生してしまいます。

提案手法

こうした課題を解決するため，以下のアプローチをとりました。

1. 高次元なモバイルNW特徴量を低次元空間へ離散化

Contextual Banditにおける重要特徴量の抽出と収束速度の向上 を目指して，以下の処理しています。

高次元かつスパースなモバイルネットワーク特徴量 $X_t\in\{0,1\}^d$ について，
まず次元圧縮（今回はPCA）により連続的な値の特徴量ベクトル $Y_t\in\mathbb{R}^{d'}$ に変換します。
さらにクラスタリング（k-means）によって，低次元な空間 $Z_t\in\{0,1\}^c$ へと離散化させました。

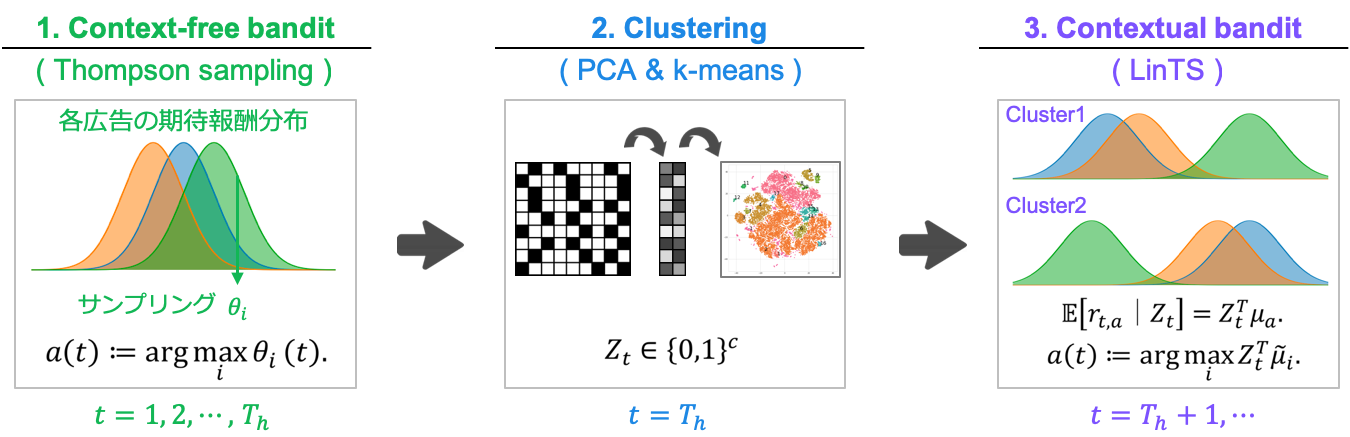
2. Context-freeとContextualのハイブリッド手法

キャンペーンサイトごとにアクセスユーザの傾向は異なるため，その都度，クラスタリングを実行することで適切な出し分け を目指します。

クラスタリングを実行するためには，ある程度データが蓄積されている必要があるため，はじめはContext-freeなBanditで運用し，アクセスユーザについてのデータを獲得します。
そして，開始から期間 $T_h$ が経った後に，蓄積したデータを基にしてクラスターを生成します．
その後の訪問ユーザ $u_t$ に対しては，所属クラスターを示すベクトル $Z_t\in\{0,1\}^c$ を計算した上で，Contextual bandit algorithmを適用します。

今回，Context-free Banditとして Thompson Sampling を, Contextual Banditとして LinTS を採用しました。
特に，Contextual Banditにおいて，各armの期待報酬は $Z_t\in\{0,1\}^c$ にたいする線形モデルである
$$\mathbb{E}[r_{t,a} | Z_t] = Z^T_t \mu_a$$
として表現できます。試行を繰り返すことで，線形モデルのパラメータは以下のように推定できます。

\hat{\mu}_a(t)=B(t)^{-1}\left(\sum^{t-1}_{\tau=1}Z_\tau\cdot r_{a,\tau}\right),\\
B(t)=I_d\sum^{t-1}_{\tau=1}Z_\tau\cdot Z_\tau^{T}

ここで，クラスタリングによって $Z_t$は低次元に圧縮されているため，逆行列 $B(t)^{-1}$ の計算負荷を抑えることができます。

効果測定

オフライン検証

弊社のグループ会社が持つ広告プラットフォーム上で，過去に実施したA/Bテストの結果を用い，提案手法のオフラインシミュレーション をしました。
データセットは2種類あり，スペインとギリシャのそれぞれのキャンペーンサイトにおけるコンバージョン結果です。また，広告の候補数はどちらも$K=2$です。

シミュレーションによるコンバージョン率の結果を次の表に示します。提案手法によってどちらのデータセットにおいても，Context-free Banditからコンバージョン率が向上していることが分かります。これにより，implicitなモバイルNW特徴量がWeb広告配信において有効であることが示せました。

実際に生成されたクラスターの特徴と，コンバージョン率の傾向についても調べました。
今回，どちらもデータセットもクラスター数は$c=4$としています。スペインのデータセットでは，NWモード,デバイスの軸で分かれている傾向で，ギリシャではNWモードとオペレータ，ブラウザーの軸で分かれている傾向にありました。
このように 適用する国やキャンペーンサイトによって，クラスター特徴は異なる ことが確かめられました。

次にコンバージョン率（CVR）を示します。スペインのデータセットでは，クラスターごとで優位な広告が異なっており，ギリシャでは，広告間のCVR差が拡大していました。この結果から，クラスター生成によって広告の出し分け効果や，学習速度の向上に寄与していると考えられます。

オンライン検証

先ほど述べた広告プラットフォームへ提案手法を導入し，オンライン環境での性能検証 をおこないました。
対象サイトは，世界9カ国の142のキャンペーンサイトで，2週間に渡って計測をおこないました。
全サイトの平均CTRの比較を表に示します。提案手法によって，オンライン環境においてもContext-free Banditからクリック率を大幅に向上することができました。

サンプルコード

Thompson samplingのcontext拡張²についてのサンプルコードです。

import numpy as np

def ind_max(x):
    m = max(x)
    return x.index(m)

class THOMPSON_CB():
    R = 0.001
    delta = 0.05

    def __init__(self, counts, values):
        self.counts = counts # 腕の選択回数
        self.values = values # 観測したCTR
        return

    def initialize(self, n_arms, n_features, n_horizon): # 初期化
        self.counts = [0 for col in range(n_arms)]
        self.values = [0.0 for col in range(n_arms)]
        self.n_features = n_features # 特徴次元数
        self.epsilon = 1 / float(math.log(n_horizon))
        self.B = dict()
        self.mu= dict()
        self.f = dict()
        return

    def select_arm(self, user): # user:featureベクトル
        n_arms = len(self.counts) # 腕の数
        prior_prob = [0.0 for arm in range(n_arms)] # 時刻tにおける各腕の事後確率

        for arm in range(n_arms):
            if self.counts[arm] == 0:
                self.B[arm] = np.identity(self.n_features)
                self.mu[arm]= np.zeros(self.n_features).reshape(self.n_features,1)
                self.f[arm] = np.zeros(self.n_features).reshape(self.n_features,1)

            b = np.array(user).reshape(self.n_features,1)
            mean = self.mu[arm].T.tolist()[0]
            v = THOMPSON_CB.R*math.sqrt((1/float(self.epsilon))*self.n_features*math.log(1/float(THOMPSON_CB.delta)))
            cov = (v**2)*np.linalg.inv(self.B[arm])

            sample_mu = np.random.multivariate_normal(mean, cov, 1).T # Sampling
            prior_prob[arm] = np.dot(b.T, sample_mu) # 事後確率 = b^(T)*sample_mu

        return ind_max(prior_prob)

    def update(self, chosen_arm, reward, user):
        self.counts[chosen_arm] = self.counts[chosen_arm] + 1
        n = self.counts[chosen_arm]

        value = self.values[chosen_arm]
        new_value = ((n - 1) / float(n)) * value + (1 / float(n)) * reward
        self.values[chosen_arm] = new_value

        b = np.array(user).reshape(self.n_features,1)
        self.B[chosen_arm] += np.dot(b, b.T) # B <- B + b・b^T
        self.f[chosen_arm] += reward*b # f <- f + r・b
        self.mu[chosen_arm] = np.dot(np.linalg.inv(self.B[chosen_arm]), self.f[chosen_arm]) # mu = B^(-1)・f
        return

さいごに

本記事では，Bandit algorithmの紹介から実システムへの適用例について述べました。
特に，特徴量を考慮したContextual Banditにおいて，特徴量自体の性質に着目して，効果的な学習と容易にサービスへ展開ができる手法 を提案しました。

Contextual Banditは，近年も多く発表がなされており，ベイジアン深層学習と組み合わせたものや⁴，深層強化学習で効率性を高めるためにContextual Banditを取り入れたもの⁵があります。また，Contextual Banditに限らず，Bandit algorithmは多くのバリエーションがあります（Adversarial Bandit, Combinatorial Banditなど）。詳しく見られたい方は，BanditBookが非常に参考になるかと思います。DeepMindの研究者が書かれたドラフト版で500ページ以上にわたって解説されています。

1. Li, Lihong, et al. "A contextual-bandit approach to personalized news article recommendation." WWW, 2010. ↩

2. Agrawal, Shipra, and Navin Goyal. "Thompson sampling for contextual bandits with linear payoffs." ICML, 2013. ↩ ↩²

3. 出水 宰，Rubén Manzano，Sergio Gómez，深澤 佑介, "モバイルネットワーク特徴量を用いた Contextual Bandit Algorithm", MBL研究会, 2018 ↩

4. Riquelme, Carlos, George Tucker, and Jasper Snoek. "Deep Bayesian Bandits Showdown." ICLR, 2018. ↩

5. Zahavy, Tom, et al. "Learn What Not to Learn: Action Elimination with Deep Reinforcement Learning." NIPS , 2018. ↩