前編の記事では，運動エネルギー汎関数$ T[n] $に対する近似式を，LDAによって明示的な形で求めました。こうすることで，電子密度だけが含まれる単純な方程式系が導かれましたが，その一方で，それを解いて得られるモデルは非常に精度が低く，実用に耐えないものでした。つまり，運動エネルギー汎関数$ T[n] $にLDAを適用したことがまずかったのです。これに対し，KohnとShamは1965年に発表した論文（参考文献[1]）で，$ T[n] $に対する巧妙（ある意味で狡智）な間接的アプローチを提案しました。この方法は，Kohn-Sham法と呼ばれ，この方法によって，密度汎関数理論は，厳密な計算を行うための実際的な道具となりました。現在では，DFTといえば専らこのKohn-Sham法のことを指し，そしてKohn-Sham法は，化学と固体・物性物理学の両分野であまねく用いられています（原子核物理学でも用いられているようです）。後編では，このKohn-Sham法について詳述したいと思います。
Kohn-Sham法
さて，KohnとShamが行ったことを一言で言えば，$ T[n] $の厳密な表式が分からないので，代わりに軌道（波動関数のようなもの）を使って運動エネルギーを求めることにした，となります。これによって，Kohn-Sham法はHohenberg-Kohnの定理や，Levyの制限付き探索で想定された純粋な密度汎関数理論ではなくなりました。にもかかわらず，外部ポテンシャルと電子密度との一対一対応を利用して変分原理で電子状態を求めるという意味で，Kohn-Sham法はHohenberg-Kohnの定理の厳密な定式化であることは強調しておくべきでしょう。
ここで，KohnとShamが行ったことを理解するには，$ N $電子系の基底状態における運動エネルギーに対する近似なしの式
T=%
%TCIMACRO{\dsum \limits_{i}^{N}}%
%BeginExpansion
{\displaystyle\sum\limits_{i}^{N}}
%EndExpansion
n_{i}%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
\phi_{i}^{\ast}\left( \vec{r},s\right) \left( -\dfrac{1}{2}\nabla
^{2}\right) \phi_{i}\left( \vec{r},s\right) d\vec{r}ds \quad(1)
から出発するのが便利でしょう（厳密性のために，ここではスピン次元を明示することにします）。ただし，Hartree原子単位系を用いました（以下，断りなしにHartree原子単位系を用いることとします）。ここで，$ \phi_{i} $と$ n_{i} $はそれぞれ自然スピン軌道とその占有数です。ここで，Pauliの原理から$ 0\leq n_{i}\leq1 $が要請されます（Kohn-Sham法では，軌道の占有数は0以上1以下の任意の実数の値を取ることができます）。一方，Hohenberg-Kohnの定理からは，$ T $が全電子密度
n\left( \vec{r}\right) =%
%TCIMACRO{\dsum \limits_{i}^{N}}%
%BeginExpansion
{\displaystyle\sum\limits_{i}^{N}}
%EndExpansion
n_{i}%
%TCIMACRO{\dsum \limits_{s}}%
%BeginExpansion
{\displaystyle\sum\limits_{s}}
%EndExpansion
\left\vert \phi_{i}\left( \vec{r},s\right) \right\vert ^{2} \quad(2)
の汎関数であることが保証されています。$ (1) $式を用いて運動エネルギーを求めようと思っても，複雑な電子同士のCoulomb相互作用のある現実の系では，$ (1) $式あるいは$ (2) $式の項数は無限個となり，簡単な場合ですら正面から取り扱うのは非常に困難です。
この問題を解決するため，KohnとShamは，相互作用のある現実の系を，仮想的な，それと同じ密度を与える相互作用のない系の問題に置き換えて考えることを提案しました。この仮想的な系は，Kohn-Shamの補助系（Kohn-Sham auxiliary system）と呼ばれます。Kohn-Shamの補助系は，相互作用のない粒子からできていますが，この系の基底状態の電子密度は，現実の系の基底状態の電子密度と，全く同じです（そう定義したのですから，当然です）。言い換えれば，Kohn-Shamの補助系は，同じ電子密度（と全エネルギー）を与える別の系です。つまり，現在用いられているKohn-Sham法では，現実の系ではなく，人間が勝手に作った仮想的な系について計算しているということです。とすると，最大の問題は，現実の系における（電子密度と全エネルギー以外の）化学的・物理的性質と，Kohn-Shamの補助系におけるそれとが，どれだけ似ているか，ということになります。この問題については，以下でおいおい議論していきたいと思います。
ところで，相互作用のある電子系の基底状態の電子密度はどのようなものでも，相互作用のない電子系の基底状態の電子密度として厳密に再現できるのでしょうか。この疑問は，「相互作用のないv表示可能性」と呼ばれます。残念なことに，この疑問に対する一般的な証明はまだありません。ここで，相互作用のないv表示可能な電子密度は，Kohn-Sham v-表示可能な電子密度と呼ばれ，単純な $ N $個の規格直交化された波動関数が作る電子密度の部分集合になっています。従って，仮に正確な$ E_{xc}[n] $の表式（後述）が得られたとしても，実在系の電子密度がKohn-Sham v-表示可能でないなら，正しい電子密度に辿り着くことはないし，従って正しいエネルギーも得られないことになります（参考文献[2]）。そして，Levyによって指摘されたように，Kohn-Sham v-表示可能ではない合理的な電子密度が存在することが知られており（参考文献[3]），実際、Kohn-Sham v-表示可能でない電子密度が見つかっています（参考文献[4]）。つまり，v表示可能性の問題は，Kohn-Sham法では解決するどころかむしろ悪化しています（当然、「基底状態の電子密度$ n_{0}(\vec{r}) $が$ v $表示可能でない場合もあり得る」のに，「個別の系で基底状態を求めたときに，$ v $表示可能な$ n_{0}(\vec{r}) $となっていることが期待される」という矛盾も解決していません）。にもかかわらず，計算結果は非常に「理にかなって」いるように見えるので，Kohn-Sham法は正しいとされています（あるいは少なくともそう仮定されています）。実際，ほとんどの非縮退原子・分子系の基底状態密度は，Kohn-Sham v-表示可能な電子密度です（参考文献[5]）。
さて，Kohn-Shamの補助系の導入により，この系の運動エネルギー汎関数$ T_{s}[n] $は，厳密に以下の式で書けるようになりました。
T_{s}\left[ n\right] =%
%TCIMACRO{\dsum \limits_{i}^{N}}%
%BeginExpansion
{\displaystyle\sum\limits_{i}^{N}}
%EndExpansion%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
\phi_{i}^{\ast}\left( \vec{r},s\right) \left( -\dfrac{1}{2}\nabla
^{2}\right) \phi_{i}\left( \vec{r},s\right) d\vec{r}ds \quad(3)
また，$ n(\vec{r}) $は下記の条件
n\left( \vec{r}\right) =%
%TCIMACRO{\dsum \limits_{i}^{N}}%
%BeginExpansion
{\displaystyle\sum\limits_{i}^{N}}
%EndExpansion%
%TCIMACRO{\dsum \limits_{s}}%
%BeginExpansion
{\displaystyle\sum\limits_{s}}
%EndExpansion
\left\vert \phi_{i}\left( \vec{r},s\right) \right\vert ^{2} \quad(4)
を満たします。ここで，前編の記事の$ (15) $式を以下のように書き換えます。
F\left[ n\right] =T_{s}\left[ n\right] +J\left[ n\right] +E_{xc}\left[
n\right] \quad(5)
ただし，
E_{xc}\left[ n\right] \equiv T\left[ n\right] -T_{s}\left[ n\right]
+V_{ee}\left[ n\right] -J\left[ n\right] \quad(6)
です。$ E_{xc}[n] $は交換相関エネルギーと呼ばれますが，これには，十分に小さいであろうと考えられる，現実の系の運動エネルギー$ T $と，Kohn-Shamの補助系における運動エネルギー$ T_{s} $の差が含まれます（これは相関エネルギーの問題に関係します。別の記事で詳しく解説します）。また，$ V_{ee} $は，複雑な電子同士のCoulomb相互作用（古典的および量子力学的相互作用の両方を含む）によるエネルギーです。Kohn-Sham法の真髄は，$ (5) $式のように，独立粒子運動エネルギー項 $ T_{s}[n] $と古典的な電子－電子間のCoulomb相互作用によるエネルギー項$ J[n] $とを陽に分割することにより，残りの交換相関エネルギー（汎関数） $ E_{xc}[n] $が，密度の局所的あるいはほぼ局所的汎関数として無理なく近似できるという点にあります（ただ，別の記事で解説するように例外はあります）。これはすなわち，交換相関エネルギー$ E_{xc}[n] $が，
E_{xc}\left[ n\right] =%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
n\left( \vec{r}\right) \epsilon_{xc}\left( \left[ n\right] ,\vec
{r}\right) \quad(7)
のように書けると言うことです。ここで$ \epsilon_{xc}([n], \vec{r}) $は位置$ \vec{r} $にある1電子あたりのエネルギーであり，それは位置$ \vec{r} $の近傍の密度$ n(\vec{r}) $にのみ依存しています。ところで，前編の記事の$ (14) $～$ (16) $式と，$ (3) $式と$ (5) $式から，Kohn-Sham法による全エネルギー（汎関数）
E_{KS}\left[ n\right] =%
%TCIMACRO{\dsum \limits_{i}^{N}}%
%BeginExpansion
{\displaystyle\sum\limits_{i}^{N}}
%EndExpansion%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
\phi_{i}^{\ast}\left( \vec{r},s\right) \left( -\dfrac{1}{2}\nabla
^{2}\right) \phi_{i}\left( \vec{r},s\right) d\vec{r}ds\mathbf{+}\dfrac
{1}{2}%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
\dfrac{n\left( \vec{r}\right) n\left( \vec{r}^{\prime}\right) }{\left\vert
\vec{r}-\vec{r}^{\prime}\right\vert }d\vec{r}d\vec{r}^{\prime}+E_{xc}\left[
n\right] +%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
v\left( \vec{r}\right) n\left( \vec{r}\right) d\vec{r} \quad(8)
が得られます。ただし，軌道$ \phi_{i}(\vec{r},s) $は次式
%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
\phi_{i}^{\ast}\left( \vec{r},s\right) \phi_{j}\left( \vec{r},s\right)
d\vec{r}ds=\delta_{ij} \quad(9)
によって規格直交化されていなければなりません。$ (8) $式と$ (9) $式から，Lagrangeの未定乗数法を用いることにより，いわゆるKohn-Sham方程式，
\left[ -\dfrac{1}{2}\nabla^{2}+v_{eff}\left( \vec{r}\right) \right]
\phi_{i}\left( \vec{r},s\right) =\varepsilon_{i}\phi_{i}\left( \vec
{r},s\right) \quad(10)
が得られます。$ (10) $式が，化学や固体・物性物理学の分野であまねく使われている方程式です。ここで，$ v_{eff}(\vec{r}) $はKohn-Sham有効ポテンシャル，$ \phi_{i}(\vec{r},s) $はKohn-Sham軌道，$ \varepsilon_{i} $はKohn-Sham軌道のエネルギー固有値です。ここで，$ v_{eff}(\vec{r}) $は，
v_{eff}\left( \vec{r}\right) =v_{ext}\left( \vec{r}\right) +v_{Hartree}%
\left( \vec{r}\right) +v_{xc}\left( \vec{r}\right) \quad(11)
によって定義されます。ここで，$ v_{ext}(\vec{r}) $は，通常は核による外部ポテンシャル，$ v_{Hartree}(\vec{r}) $は古典的な電子－電子間のCoulomb相互作用によるポテンシャル（Hartreeポテンシャル）で，
v_{Hartree}\left( \vec{r}\right) =%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
\dfrac{n\left( \vec{r}^{\prime}\right) }{\left\vert \vec{r}-\vec{r}^{\prime
}\right\vert }d\vec{r}^{\prime} \quad(12)
で定義されます。さらに，$ v_{xc}(\vec{r}) $は以下の式
v_{xc}\left( \vec{r}\right) =\dfrac{\delta E_{xc}\left[ n\right] }{\delta
n\left( \vec{r}\right) } \quad(13)
で定義され，交換相関ポテンシャルと呼ばれます。$ (10) $式，$ (11) $式，$ (13) $式で重要なことは，ポストHartree-Fock法において，基底状態と励起状態との電子配置間の相互作用として取り込まれてきた電子相関を，Kohn-Sham方程式では，ポテンシャル汎関数として簡便に取り込んでいることです。また，Kohn-Sham方程式の固有関数（≒波動関数）は問題の解として得られますが，固有関数はKohn-Sham有効ポテンシャル$ v_{eff}(\vec{r}) $の計算に必要な電荷密度を構築する際にも必要なので，Kohn-Sham方程式は強く非線形になっていて，解析的に解くことができないことも重要です。またここで，$ (8) $式を，$ \varepsilon_{i} $を含む形で書き直すと，Kohn-Sham法による全エネルギー$ E_{KS}[n] $は，
E_{KS}\left[ n\right] =%
%TCIMACRO{\dsum \limits_{i}^{N}}%
%BeginExpansion
{\displaystyle\sum\limits_{i}^{N}}
%EndExpansion
\varepsilon_{i}-\dfrac{1}{2}%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
\dfrac{n\left( \vec{r}\right) n\left( \vec{r}^{\prime}\right) }{\left\vert
\vec{r}-\vec{r}^{\prime}\right\vert }d\vec{r}d\vec{r}^{\prime}+E_{xc}\left[
n\right] -%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
v_{xc}\left( \vec{r}\right) n\left( \vec{r}\right) d\vec{r} \quad(14)
となります。ここで，右辺第1項はKohn-Sham方程式のエネルギー固有値の総和，右辺第2項はHartreeエネルギー，右辺第3項は交換相関エネルギー，右辺第4項は交換相関ポテンシャルの期待値です。$ (14) $式を見ると分かりますが，Kohn-Sham法による全エネルギーは，単純に各Kohn-Sham軌道のエネルギー固有値の総和とならないことに注意してください（なおこれは，Hartree-Fock法にも言えることです）。なお，鋭い方なら，$ (14) $式の右辺第4項と，右辺第5項は，相殺されて消えるのではないか，と思われるかもしれません。ところが，一般にそうはなりません。この点については，また別の記事で議論します。
ところで，勘違いしないようにして頂きたいのですが，Kohn-Shamの補助系における相互作用のない系とは，電子－電子間の相互作用を全て無視するという意味ではありません。例えば，他の電子から受ける古典的なCoulomb相互作用は，Kohn-Sham方程式において，Hartreeポテンシャルとして取り入れられています（$ (11) $式）。これは，電子の平均的な電荷分布から生じる静電ポテンシャルです。ところで，Kohn-Sham方程式には，直接的な電子－電子間の相互作用の項が含まれていません。結果として，Kohn-Sham方程式は，Hartree-Fock方程式と同じように，一電子に対するSchrödinger方程式の形をしています（独立電子近似）。これを「相互作用のない」と呼んでいます。
なお$ (10) $式は，前々回の記事で解説したHartree-Fock方程式と同様に，非線形偏微分方程式であり，一般に解析的はおろか，そのままでは数値的にも解けません。従って，Kohn-Sham方程式を解く際は，Hartree-Fock方程式のときと同様，専ら基底で展開し，行列方程式に変換して，自己無撞着に解くという方法が用いられます。
さて，$ (10) $式で注意すべきなのは，Kohn-Sham軌道$ \phi_{i}(\vec{r},s) $は，直接には，どんな物理的な意味も持っていないと言うことです。Kohn-Sham軌道は，相互作用のない補助系の電子軌道であり，実際の系の電子に対する波動関数であると考えることはできません。実際，結晶の巨視的な分極は，電子密度のみから求めることは困難であり，波動関数の位相が必要であることが知られていますが，これはKohn-Sham軌道からは正しく与えられません。
なお，前編の記事で「私の中での密度汎関数理論の未解決問題」として例に出した，「電子密度$ n(\vec{r}) $から，多体波動関数$ \psi(\vec{r}_{1},\vec{r}_{2,\ldots,}\vec{r}_{N}) $をどう決定するか」という問題は，Kohn-Sham法では，電子密度から多体波動関数を得るのに，Kohn-Sham軌道のSlater行列式を作ってやれば良いだけなので，解決したことになります．
さらにこれは，Kohn-Sham方程式のエネルギー固有値$ \varepsilon_{i} $にも言えることであり，Kohn-Sham方程式のエネルギー固有値は，直接にはどんな物理的な意味も持っていません。従って，Kohn-Sham方程式のエネルギー固有値を，実際の系のものと見なすことはできません。つまり，Kohn-Sham法で計算した分子軌道ダイアグラムや，固体におけるバンド分散の図は，現実の系のものと見なすことはできません。ただし，これには例外があり，有限の系に対する最も高いエネルギー固有値$ \varepsilon_{max} $は，系のイオン化エネルギー$ I $の符号を変えたものと等しくなります。つまり，
\varepsilon_{max}=-I \quad(15)
です。これは，有限な系の長距離での漸近的密度は$ \varepsilon_{max} $（あるいは$ -I $）によって決められるという要請，
n\left( \vec{r}\right) \sim\exp\left[ -2\left( -2\varepsilon_{max}\right)
^{\frac{1}{2}}r\right] =\exp\left[ -2\left( 2I\right) ^{\frac{1}{2}%
}r\right] \quad(16)
から来るものです。ただし，この規則は厳密な交換相関汎関数を用いたKohn-Sham法によって初めて成り立つものであり，一般のKohn-Sham法では，$ (15) $式あるいは$ (16) $式は成り立ちません。この点については，別の記事でより詳細に議論します。
さて上記で，「Kohn-Sham方程式のエネルギー固有値は，直接にはどんな物理的な意味も持っていません」と書きましたが，実際には，Kohn-Sham方程式のエネルギー固有値は，実験値とよく比較されます。この根拠は，以下のJanakの定理
\dfrac{\partial E_{KS}}{\partial n_{i}}=\varepsilon_{i} \quad(17)
です（$ n_{i} $は，$ (1) $式で出てきた軌道の占有数です）。ここで，イオン化エネルギーを，$ i $番目の軌道$ \phi_{i}(\vec{r}) $から，電子を1個取り去るためのエネルギーだと定義します。この記事で説明した，Hartree-Fock法におけるKoopmansの定理によれば，
E^{N}-E^{N-1}=\varepsilon_{i} \quad(18)
であり，この$ \varepsilon_{i} $は，イオン化エネルギーの逆符号と等しいことが分かります。ここで，$ E^{N} $はN個の電子からなる系の基底状態における全エネルギーであり， $ E^{N-1} $は，その系から電子を1個取り出した場合，つまりN-1個の電子からなる系の全エネルギーです（ただし，電子を取り去ることに対し，一電子波動関数は不変であると仮定しています（つまり，電子の緩和効果は無視できると仮定しています））。ここで，$ (17) $式の左辺は差分ではなく微分になっており，このため，エネルギー固有値$ \varepsilon_{i} $はイオン化エネルギーの逆符号であるとは言えません。しかし同時に，差分と微分の差が小さいと仮定して，
\dfrac{\partial E_{KS}}{\partial n_{i}}\approx E_{KS}^{N}-E_{KS}%
^{N-1}=\varepsilon_{i} \quad(19)
とすれば，Kohn-Sham法においても，エネルギー固有値$ \varepsilon_{i} $を，イオン化エネルギーの逆符号と見立てても良いということになります（上述のように，有限の系に対する最も高いエネルギー固有値$ \varepsilon_{max} $に対しては，$ (19) $式が厳密に成り立ちます（あくまで，厳密な交換相関汎関数を用いた場合のことですが））。 なお，ここで注意すべきなのは，$ (17) $式のJanakの定理においては，Koopmansの定理のように，電子数の変化に対して一電子波動関数が不変である，という仮定（＝電子の緩和効果が無視できるという仮定）が不要であることです。このJanakの定理により，Kohn-Sham法で計算した分子軌道ダイアグラムや，固体におけるバンド分散の図を，実験結果と比較することがある程度正当化されます。
さて，ここまでの議論では，交換相関エネルギー$ E_{xc}[n] $（あるいは交換相関ポテンシャル$ v_{xc}(\vec{r}) $）の明示的な表式については明らかにしてきませんでした。ここで，$ E_{xc}[n] $は，次式のように交換と相関の寄与に分解することができ，
E_{xc}\left[ n\right] =E_{x}\left[ n\right] +E_{c}\left[ n\right] \quad(20)
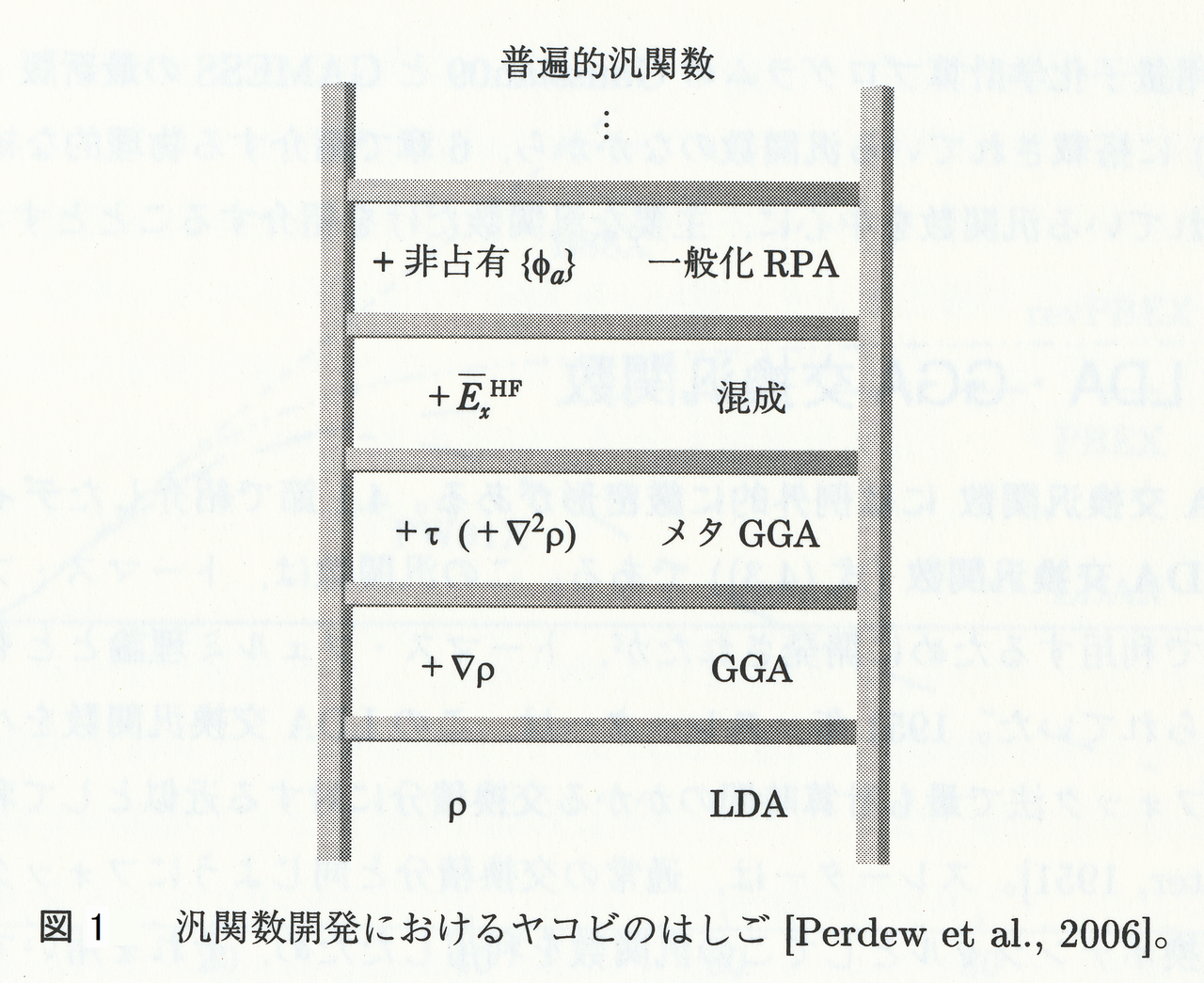
となります。$ (20) $式の$ E_{x}[n] $は，交換エネルギーと呼ばれ，同種Fermi粒子の間で働く相互作用の一つ（交換相互作用）によるエネルギーであり，純粋に量子力学的な効果です。また，$ E_{c}[n] $は，運動エネルギー，Coulomb相互作用，そして交換相互作用以外の全ての相互作用（量子多体問題と深い関係がある）によるエネルギーであり，相関エネルギーと呼ばれています。相関エネルギーという言葉自体は，この記事や，この記事でも出てきましたが，密度汎関数理論における相関エネルギーは，Hartree-Fock法のそれと比べて，定義が違っています。なぜなら，上述したように，密度汎関数理論における相関エネルギーには，現実の系の運動エネルギー$ T $と，Kohn-Shamの補助系における運動エネルギー$ T_{s} $の差，$ T - T_{s} $が含まれているからです（$ T - T_{s} $は必ず正の値を取ります）。ところで，$ E_{xc}[n] $（または$ v_{xc}(\vec{r}) $）は一般に交換相関汎関数と呼ばれ，Kohn-Sham法において最も重要な項ですが，残念なことに厳密な表式は未だに導かれていません。しかし，交換相関汎関数については，過去数十年にわたって改善され続けてきた歴史があり，また現在でもそれは続いています。ただしこの結果，多種多様な交換相関汎関数が乱立することになってしまいました。ところで，その交換相関汎関数は階層的に分類することができ，この様子は，新約聖書の一節になぞらえて，「ヤコビのはしご（Jacob's ladder）」と呼ばれています（下図）。
上図は参考文献[6]から引用しました。ここで，ヤコビのはしごの下の段から，それぞれの汎関数の特徴を簡単に説明しますと，
- LDA（Local Density Approximation，局所密度近似）：最も簡単な交換相関汎関数であり，電子密度$ n(\vec{r}) $のみに依存します。LDA相関汎関数は，二種類のスピン密度$ n^{\alpha}(\vec{r}) $および$ n^{\beta}(\vec{r}) $に依存するので，正確には，局所密度近似ではなくLSDA（Local Spin Density Approximation, 局所スピン密度近似）です。しかし，実際にはLSDAも，総じてLDAと呼ばれています。ここには，前編の記事で出てきたDiracの交換汎関数（歴史的経緯からSlaterの交換汎関数と呼ばれることが多い），VWN相関汎関数，PW92相関汎関数などが含まれます。
- GGA（Generalized Gradient Approximation，一般化勾配近似）：LDAを，電子密度の勾配$ \nabla n( \vec{r}) $を用いて補正した交換相関汎関数です。ここには，B88交換汎関数，LYP相関汎関数，PBE交換相関汎関数，PW91交換相関汎関数などが含まれます。
- meta-GGA（メタGGA）：GGAを，運動エネルギー密度$ \tau $（あるいは電子密度のラプラシアン$ \nabla^{2} n(\vec{r}) $）を用いて補正した交換相関汎関数です。ここには，PKZB交換相関汎関数，TPSS交換相関汎関数，KCIS相関汎関数，mBJ交換相関汎関数，M06-L交換相関汎関数などが含まれます。
- Hybrid functional（混成汎関数）：LDA，GGAやメタGGAの交換項を，Hartree-Fock交換を一定の割合で混ぜることにより補正した交換相関汎関数です（厳密には，Hartree-Fock交換とGGA交換との間に厳密交換が存在しているという「仮定」が基本にある汎関数を指します）。相関項については，LDA，GGAやメタGGAのものをそのまま用います。ここには，B3LYP交換相関汎関数，PBE0交換相関汎関数，HSE交換相関汎関数，M06-2X交換相関汎関数などが含まれます。
- 一般化RPA：RPAとは，乱雑位相近似（Random Phase Approximation） の略です。混成汎関数では，Kohn-Sham占有軌道のみを用いていましたが，RPAではそれに加えてKohn-Sham仮想軌道も用います。Kohn-Sham仮想軌道を用いるという意味で，GGA交換相関項にHartree-Fock交換に加え，Møller–Plesset (MP2)の相関を混ぜた，ダブルハイブリッド汎関数（B2PLYPなど）もここに分類されます（参考サイト[1]）。
となります。図1で重要なことは，文字通りに受け取るならば，下の段から上の段にいくと汎関数は，常により良いものとなると解釈できるのですが，必ずしもそうではないことです（参考文献[7]）。特に，上の段の汎関数が経験的な場合は，下の段の汎関数の方がより精確な結果を与える場合も多々あります（一般に，上の段の汎関数ほど経験的パラメータが増える傾向があります）。例えば，GGAはLDAよりも精確な結果を与えるとしばしば仮定されています。これは多くの場合正しいのですが，例外もあり，例えば，遷移金属と酸化物の表面エネルギーの計算では，GGAよりLDAの方が良い結果を与えます（参考文献[8]）。つまり，年を経るごとにヤコビのはしごを上るように普遍的な汎関数に着実に近づいており，結果として最新の汎関数のほうが優れている，と考えるのはあまりにも楽観的すぎると言えます。これは，摂動の高次項を計算することで，系統的に解の精度を改良できるのが特長である，ポストHartree-Fock法とは好対照です。
またまた記事が長くなってしまったので，この記事はこれで終わりにしたいと思います。個々の汎関数の詳細な説明は，次回の記事を楽しみにお待ち下さい（「できるだけ簡単に密度汎関数理論（Density Functional Theory, DFT）の汎関数について説明してみる」というタイトルになる予定です）。
なお，GTOを用いたLDA-VWN汎関数による水素原子のエネルギーの計算の記事と，[GTOを用いたLDA-VWN汎関数によるヘリウム原子のエネルギーの計算の記事]
(https://qiita.com/dc1394/items/8cf5ffc5eee42ad849a2 "局所密度近似（LDA）でヘリウム原子のエネルギーを計算してみる（C++17のソースコード付き）")もQiitaに投稿しましたので，こちらも合わせてお読みいただければと思います。
#参考文献
[1] W. Kohn and L. J. Sham, Phys. Rev. 140, A1133 (1965).
doi:10.1103/PhysRev.140.A1133
[2] 高橋英明, 分子シミュレーション研究会会誌「アンサンブル」16(1) 51-54 (2014).
doi:10.11436/mssj.16.51
[3] M. Levy, Phys. Rev. A 26, 1200 (1982).
doi:10.1103/PhysRevA.26.1200
[4] A. Schindlmayr and R. W. Godby, Phys. Rev. B 51, 10427 (1995).
doi:10.1103/PhysRevB.51.10427
[5] R. C. Morrison, J. Chem. Phys. 117, 10506 (2002).
doi:10.1063/1.1520136
[6] 常田貴夫『密度汎関数法の基礎』講談社（2012）
[7] D.S.ショール, J.A.ステッケル『密度汎関数理論入門: 理論とその応用』吉岡書店（2014）
[8] D. Alfé and M. J. Gillan, J. Phys. Condens. Matt. 18, L435 (2006).
doi:10.1088/0953-8984/18/35/L01
[9] R.G.パール, W.ヤング 『原子･分子の密度汎関数法』シュプリンガー・フェアラーク東京（1996）
[10] R.M.マーチン 『物質の電子状態 上』シュプリンガー・ジャパン株式会社（2010）
#参考サイト
[1] ダブルハイブリッド密度汎関数理論 doubly hybrid density functional theory - 計算化学.com