この記事では,前回、前々回の記事で解説したHartree-Fock法と双璧をなす理論である,密度汎関数理論(Density Functional Theory, DFT)を,できるだけ簡単(?)に説明していきたいと思います。が,その前にまず,
Hartree-Fock法に電子相関を取り込む方法について,簡単に紹介したいと思います。
序論 ポストHartree-Fock法から密度汎関数理論へ
前回の記事で,Hartree-Fock法では電子相関が無視されており,これがしばしば非物理的な結果をもたらす,と述べました。では,Hartree-Fock法で欠けていた電子相関を取り込むには,一体どうすれば良いのでしょうか。
結論から言うと,「基底状態の電子配置に,励起状態の電子配置を加える」という考え方から導かれた,Hartree-Fock法を拡張した理論によって,電子相関を取り込むことが可能です。具体的には,摂動法によって励起配置に由来する電子相関を考慮したり(Møller–Plesset法),基底状態の電子配置の軌道(=Hartree-Fock軌道)から構成されたSlater行列式に,励起演算子を作用させることにより電子相関を考慮したり(結合クラスター(Coupled Cluster, CC)法),基底状態の電子配置の軌道から構成されたSlater行列式と,励起状態の電子配置の軌道から構成された複数のSlater行列式の線形結合を用いることによって,電子相関を考慮したりします(配置間相互作用(Configuration Interaction, CI)法,やMCSCF(Multi-Configurational Self-Consistent Field)法の一種であるCASSCF(Complete Active Space Self-Consistent Field)法)。
これらの方法は,ポストHartree-Fock法と総称されますが,電子相関を精度良く取り込める代わりに,計算コストが非常に大きいのが欠点です。具体的な計算量のオーダーとしては,基底の数を$ N $とすると,ランダウの記号を用いて,CASSCF法は$ O(N^{5}) $,Møller–Plesset法は$ O(N^{5}) $以上,結合クラスター法や配置間相互作用法は$ O(N^{6}) $以上と,Hartree-Fock法の$ O(N^{4}) $と比べて,どうしても計算コストが大きくなってしまうのが大問題です(この計算量のオーダーについては,参考文献[1]から引用しました)。
では,基底状態の電子配置のみを考え(つまりこれは,単一Slater行列式を用いて,全波動関数を固有値の低い方からN個の一電子波動関数で構築するということです),かつ一電子方程式を解くことのみで電子相関を取り込むことはできないのでしょうか。結論から言うと,これは可能であり,その方法が以下で詳しく説明する,密度汎関数理論(のうちのKohn-Sham法)です。
密度汎関数理論(Density Functional Theory, DFT)とは何か
密度汎関数理論を一言で言うと,系のあらゆる物理量(性質)は,基底状態の電子密度の一義に決まる汎関数であるというものです。これだけでは何のことかさっぱり分からないと思いますので,まずは前々回の記事で,Hartree-Fock法を解説する際に出発点として用いた,ヘリウム原子に対するSchrödinger方程式を例にとって,密度汎関数理論について解説していくことにします。なお,密度汎関数理論の概略のみ知りたい方は,拙著のスライドをご覧になった方がよろしいかと思います。
Hartree原子単位系を用いると(以下,断りなしにHartree原子単位系を用いることとします),(Born-Oppenheimer近似の下で)ヘリウム原子に対するSchrödinger方程式は,
\left[ -\dfrac{1}{2}\nabla_{1}^{2}-\dfrac{1}{2}\nabla_{2}^{2}-\dfrac
{2}{r_{1}}-\dfrac{2}{r_{2}}+\dfrac{1}{\left\vert \vec{r}_{1}-\vec{r}%
_{2}\right\vert }\right] \psi\left( \vec{x}_{1},\vec{x}_{2}\right)
=E\psi\left( \vec{x}_{1},\vec{x}_{2}\right) \quad(1)
と書けます。ここで,この方程式は3次元×2=6次元の偏微分方程式です(スピン次元については,とりあえず横に置いておきます)。前々回の記事で解説したHartree-Fock法では,$ (1) $式を「変数分離」できるとして近似することで,3次元の偏微分方程式に帰着させたわけですが,その代償として,電子相関を取りこぼしてしまったのでした。
では,$ (1) $式を近似なしに直接解くことはできないのでしょうか。結論から言えば,これは可能です。実際,$ (1) $式を,近似なしに有限要素法で解いた論文が存在します(参考文献[2])。しかし,ヘリウム原子の場合は近似なしに数値的に解けるとしても,一般にN電子系では,3N次元のSchrödinger方程式を解かなければならないので,一般の多電子原子,あるいは分子となると,事情が全く違ってきます。例えば,リチウム原子では9次元,ベリリウム原子では12次元,そして周期表のずっと下の方,例えばウラン原子では,3次元×92=276次元の偏微分方程式を解かなければなりません。さらに,分子となると,例えばタンパク質などの高分子に対しては,数万次元の偏微分方程式を解かなければならなくなります。つまり,一般の多電子原子や分子に対するSchrödinger方程式を,近似なしに有限要素法などで解くのは,計算量が莫大になるため不可能です(また,一般の3N次元のSchrödinger方程式を近似なしに解くときは,計算途中の式も,人の手では扱えないほど恐ろしく複雑になることでしょう)。
困りました。何か良い方法はないでしょうか。ここで,冷静になって考えてみると,多電子原子(あるいは分子)に対するSchrödinger方程式が,3N次元の偏微分方程式になってしまうのは,波動関数が3Nの次元を有するからです。つまり,3N次元の多体波動関数$ \psi(\vec{r}_{1},\vec{r}_{2,\ldots,}\vec{r}_{N}) $を近似なしに求めることにこだわる限り,絶対に3N次元の偏微分方程式を解かなければならないのです(細かいことを言うと,前述したCI法の一種であるFull CI法を使えば,一般のN電子系であっても3次元の電子軌道のSlater行列式の線形結合から,3N次元のSchrödinger方程式の近似なしの解が得られますが,計算量が莫大になるという点は全く変わりません)。仕方がないので,ここで発想の大転換を行います。具体的には,多体波動関数$ \psi(\vec{r}_{1},\vec{r}_{2,\ldots,}\vec{r}_{N}) $の代わりに,以下の式
n\left( \vec{r}\right) \equiv N%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
\cdots%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
\psi^{\ast}\left( \vec{r}_{1},\vec{r}_{2,\ldots,}\vec{r}_{N}\right)
\psi\left( \vec{r}_{1},\vec{r}_{2,\ldots,}\vec{r}_{N}\right) d\vec{r}%
_{2}\cdots d\vec{r}_{N} \quad(2)
で定義される3次元の電子密度$ n(\vec{r}) $を「基本的な変数」として考えます。通常の量子力学では,「電子密度は粒子の存在確率を表す」と習いますが(Bornの確率解釈),これに加えて,電子密度$ n(\vec{r}) $には,多体波動関数$ \psi(\vec{r}_{1},\vec{r}_{2,\ldots,}\vec{r}_{N}) $の有する全ての情報が含まれていると考えるのです。もしこの考え方が正しいならば,複雑な3N次元の多体波動関数を求める代わりに,3次元の関数である電子密度を求めれば良いので,問題が著しく簡単になることが期待されます。さて問題は,このような考え方は果たして正しいのかどうか,仮に正しいとしてそれを数学的に定式化できるのかどうかです。これらについては,次節で詳しく解説したいと思います。
Hohenberg-Kohnの定理
前節の最後で述べた問題は,1964年にHohenbergとKohnが発表した記念碑的な論文(参考文献[3])によって,見事に解決されました。具体的には,同論文でHohenbergとKohnは,以下の定理が成り立つことを示しました。
- エネルギーの零点の取り方を除いて,基底状態の電子密度$ n_{0}(\vec{r}) $から外部ポテンシャル$ v(\vec{r}) $が決定される。
この定理は,現在ではHohenberg-Kohnの第一定理と呼ばれています。ここで,物質中の電子に対しては,外部ポテンシャルというのは要するに(原子)核によるCoulombポテンシャルです。また,この定理からは,外部ポテンシャル$ v(\vec{r}) $のみならず,基底状態のHamiltonian演算子$ \hat{H} $すらも,基底状態の電子密度$ n_{0}(\vec{r}) $によって決定されることが導かれます。証明は背理法によりますが,この記事では割愛します。ただし,この定理の証明に際し,重要な二つの仮定が用いられていることには注意するべきでしょう。二つの仮定とは,
- $ N $電子系の基底状態が縮退していないこと(非縮退基底状態の仮定)
- 任意の電子密度$ n(\vec{r}) $を与えると,必ず,それを基底状態の電子密度とするような$ v(\vec{r}) $が一つは存在すること($ v $表示可能性の仮定)
です。これらの仮定の妥当性については,後述したいと思います。さて,この定理はつまるところ,基底状態の電子密度$ n_{0}(\vec{r}) $と,外部ポテンシャル$ v(\vec{r}) $が一対一対応する,ということを述べています。もっと言うと,基底状態の電子密度$ n_{0}(\vec{r}) $と,基底状態の多体波動関数$ \psi_{0}(\vec{r}_{1},\vec{r}_{2,\ldots,}\vec{r}_{N}) $は,外部ポテンシャル$ v(\vec{r}) $を通じて一対一対応するということです。このことは,系のすべての物理量は基底状態の電子密度$ n_{0}(\vec{r}) $を与えれば一意的に決まるもの,即ち電子密度の汎関数であると言うことを意味しています(汎関数についての説明は割愛しますが,Googleで検索すれば情報はいくらでも得られます)。しかし,$ n_{0}(\vec{r}) $を実際に決定する際に,対応する多体波動関数$ \psi_{0}(\vec{r}_{1},\vec{r}_{2,\ldots,}\vec{r}_{N}) $の情報が必要とされるのであれば,上記の定理は実際にはあまり意味をなさないでしょう。また,上記の定理は,要するに電子密度は(原子)核の位置と種類を一義に決めるということを意味していますが,実はこの程度のことは通常の量子力学(加藤の定理)を用いれば簡単に証明できます。
従って,同論文で真に驚くべきは,多体波動関数$ \psi(\vec{r}_{1},\vec{r}_{2,\ldots,}\vec{r}_{N}) $の情報を一切必要とせずに,$ n_{0}(\vec{r}) $を求めるプロセスを提示した以下の定理です。
- どのような外部ポテンシャル$ v(\vec{r}) $に対しても成り立つ,電子密度の汎関数$ E_{HK}[n] $(Hohenberg-Kohnの「普遍的な」エネルギー汎関数)が存在する。どのような$ v(\vec{r}) $に対しても系の厳密な基底状態のエネルギーはこの汎関数の大局的な極小値であり,汎関数を最小にする電子密度$ n(\vec{r}) $は厳密に基底状態の電子密度$ n_{0}(\vec{r}) $である。
これは,Hohenberg-Kohnの第二定理と呼ばれています(証明は第一定理と同じく背理法によりますが,割愛します)。長々と難しいことが書いてありますが,この定理の言わんとしていることは,要するに,種々の電子密度$ n(\vec{r}) $があり得るが,$ E_{HK}[n] $に代入すれば,得られるエネルギーが最小となるような電子密度$ n_{0}(\vec{r}) $が,系の基底状態の電子密度(=3N次元のSchrödinger方程式の基底状態の解である多体波動関数$ \psi_{0}(\vec{r}_{1},\vec{r}_{2,\ldots,}\vec{r}_{N}) $に対応)であり「正解」である。従って,電子密度$ n(\vec{r}) $を色々と変化させて,そのような電子密度$ n_{0}(\vec{r}) $を何とかして探し出せばよい,と言うことです。ここで,この定理を数学的に定式化すると,電子密度$ n(\vec{r}) $を全空間で積分すると全電子数Nになるという拘束条件
%
%TCIMACRO{\dint}%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
n\left(\vec{r}\right)d\vec{r} = N \quad(3)
の下で,$ E_{HK}[n] $を最小化することになります。すなわち,Lagrangeの未定乗数法を使って,電子密度$ n(\vec{r}) $が停留条件
\delta\left\{ E_{HK}\left[ n\right] -\mu\left[
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
n\left( \vec{r}\right) d\vec{r}-N\right] \right\} =0 \quad(4)
を満たすとき,これは「正解」の基底状態の電子密度$ n_{0}(\vec{r}) $であり,一意的に定まります。ここで,$ \mu $はLagrangeの乗数(物理的には化学ポテンシャルあるいはFermiエネルギー)です。さて,$ (4) $式をよく見てみると,通常のSchrödinger方程式を使った量子力学と,ほとんど変わらないことが分かります。すなわち,多体波動関数$ \psi(\vec{r}_{1},\vec{r}_{2,\ldots,}\vec{r}_{N}) $が,$ 1 $に規格化されていなければならないという拘束条件
%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
\cdots%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
\psi^{\ast}\left( \vec{r}_{1},\vec{r}_{2,\ldots,}\vec{r}_{N}\right)
\psi\left( \vec{r}_{1},\vec{r}_{2,\ldots,}\vec{r}_{N}\right) d\vec{r}%
_{1}d\vec{r}_{2}\cdots d\vec{r}_{N}=1 \quad(5)
の下で,ハミルトニアン$ \hat{H} $の期待値の汎関数(=エネルギー汎関数)
\varepsilon\left[ \psi\right] =%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
\cdots%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
\psi^{\ast}\left( \vec{r}_{1},\vec{r}_{2,\ldots,}\vec{r}_{N}\right) \hat
{H}\psi\left( \vec{r}_{1},\vec{r}_{2,\ldots,}\vec{r}_{N}\right) d\vec{r}%
_{1}d\vec{r}_{2}\cdots d\vec{r}_{N} \quad(6)
を最小化する問題を考えます。すると,多体波動関数$ \psi(\vec{r}_{1},\vec{r}_{2,\ldots,}\vec{r}_{N}) $が,停留条件
\delta\left\{ \varepsilon\left[ \psi\right] -E\left[
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
\cdots%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
\psi^{\ast}\left( \vec{r}_{1},\vec{r}_{2,\ldots,}\vec{r}_{N}\right)
\psi\left( \vec{r}_{1},\vec{r}_{2,\ldots,}\vec{r}_{N}\right) d\vec{r}%
_{1}d\vec{r}_{2}\cdots d\vec{r}_{N}-1\right] \right\} =0 \quad(7)
を満たすときの多体波動関数$ \psi_{0}\left( \vec{r}_{1},\vec{r}_{2,\ldots,}\vec{r}_{N}\right) $は,3N次元のSchrödinger方程式の基底状態の解となります(参考サイト[1])。ここで,$ E $はLagrangeの乗数であり,物理的にはエネルギー期待値です。$ (7) $式と$ (4) $式は良く似ており,両者を比較すると,通常の量子力学と密度汎関数理論の違いは,少なくともエネルギーに関していえば,前者はエネルギーを多体波動関数の汎関数と見なすが,後者はエネルギーを電子密度の汎関数と見なす,という点だけである,ということが分かると思います。
さて,3N次元のSchrödinger方程式を直接解く代わりに,$ (4) $式を解けば,万事上手く行くことが分かったので,(自然に)勝ったッ!(最初の記事から数えて)第3部完!…としたいところですが,そうは問屋が卸しません。なぜならば,Hohenberg-Kohnの「普遍的な」エネルギー汎関数$ E_{HK}[n] $の厳密な表式(通常の量子力学における$ (6) $式に相当するもの)は,全く知られていないからです。これには理由があり,$ E_{HK}[n] $を見つけるための手段は,多体波動関数$ \psi(\vec{r}_{1},\vec{r}_{2,\ldots,}\vec{r}_{N}) $を使ったもとの定義より他には,全く与えられていないのです。加えて,$ E_{HK}[n] $のすべての部分は,電子数の関数として非解析的な振る舞いをするでしょう。従って,そのような$ E_{HK}[n] $の厳密な表式を求めることは極めて困難です。
さらに,仮に$ E_{HK}[n] $の厳密な表式が得られたとしても,そこから得られる情報は,系の基底状態の電子密度と基底エネルギーのみであり,これら以外の物理量に関しては一切情報が得られないことも大問題です(系の基底状態の電子密度と基底エネルギー以外の,任意の物理量$ X $の基底状態での値は,前述のように,原理的にはエネルギーと同様,「正解」の基底状態の電子密度$ n_{0}(\vec{r}) $の汎関数$ X[n_{0}] $として与えられるのですが,肝心の$ X[n_{0}] $の表式については,厳密式どころか,近似式すら得られていないのです)。
現在でも,「普遍的な」エネルギー汎関数$ E_{HK}[n] $を求めるべく努力が続けられていますが,現状では近似汎関数が用いられています。というわけで以下では,$ E_{HK}[n] $の近似汎関数について,解説していきたいと思います。が,その前に,Hohenberg-Kohnの第一定理を証明する際に用いた二つの仮定について,その妥当性を次節にて検討していくことにしましょう。
v表示可能性とLevyの制限付き探索
前節で,Hohenberg-Kohnの第一定理を証明する際に二つの仮定を用いましたが,このうち非縮退基底状態の仮定については,取り除くことが可能であることを,1985年にKohn自身が証明しました(証明は例によって割愛します)。従って現在では,たとえ基底状態が縮退していたとしても,基底状態の電子密度$ n_{0}(\vec{r}) $に対して外部ポテンシャル$ v(\vec{r}) $は一意的に定まるので,密度汎関数理論が成り立つことが分かっています。
しかし,もう一つの$ v $表示可能性の仮定については,これは難しい問題($ v $表示可能性問題と呼ばれています)です。$ v $表示可能性問題とは要するに,いかなる外部ポテンシャル$ v(\vec{r}) $を持ってしても,基底状態のものとしては表現できない電子密度$ n(\vec{r}) $があるのではないか(=外部ポテンシャル$ v(\vec{r}) $の下でSchrödinger方程式を解いて求まった多体波動関数を,$ (2) $式に代入することにより電子密度$ n(\vec{r}) $が得られるが,そもそもSchrödinger方程式の基底状態の解(を$ (2) $式に代入したもの)になっていない$ n(\vec{r}) $があるのではないか)というものです。 HohenbergとKohn自身,そのことを気にしていましたが,最初の証明では「そのような病的な電子密度$ n(\vec{r}) $は物理的には興味がないものであり,考える必要がない」とバッサリ切り捨てています。しかしこの問題は後になって,一時は密度汎関数理論の厳密性に疑問が呈されたほどに数学的には深刻に考えられました(実際,$ v $表示可能ではありませんが,物理的にはもっともらしい$ n(\vec{r}) $が多数存在することが証明されました(反例が明示されました))。
このことは,密度変分原理($ (4) $式)に深刻な影響を及ぼすことになりました。なぜなら,これまでの証明法では,$ v $表示可能でない$ n(\vec{r}) $については密度変分原理が成り立つかどうかわからないからです。また,それなら$ v $表示可能である$ n(\vec{r}) $の範囲でのみ変分探索を実行しようと思っても,$ n(\vec{r}) $が具体的に与えられたときに,それが$ v $表示可能であるかどうかは簡単には分かりません($ n(\vec{r}) $が$ v $表示可能であることの必要十分条件は全く知られていません。ただ,必要条件なら得られています。後述)。
これは,仮に$ v $表示可能な$ n(\vec{r}) $を初期電子密度として変分探索を開始したとしても,変分探索の途中で$ n(\vec{r}) $が$ v $表示可能でなくなってしまうことも考えられるということです。従って,変分探索の毎ステップごとに$ n(\vec{r}) $が$ v $表示可能かどうかを一々チェックしなければならないことになりますが,これはそのための計算量を鑑みると非現実的です。さらに,仮に$ n(\vec{r}) $が$ v $表示可能かどうかが簡単に分かったとしても,基底状態の電子密度$ n_{0}(\vec{r}) $が$ v $表示可能でない場合(純状態$ v $表示不可能)には,最低エネルギー状態を与える$ n_{0}(\vec{r}) $が変分の探索範囲にない(それゆえ,探索が決して終了しないか,たまたま終了したとしても正しい結果が得られない)ことになります。
前述の困難を打破するため,LevyとLiebは,$ E_{HK}[n] $を,$ v $表示可能な範囲より広い$ N $表示可能(後述)な範囲で,密度変分原理が適用可能な形に書き直しました(参考文献[4],参考文献[5])。LevyとLiebは,
F_{LL}\left[ n\right] =\min\limits_{\psi\rightarrow n\left( \vec
{r}\right) }%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
\psi_{n\left( \vec{r}\right) }^{\ast}\left( \vec{r}_{1},\vec{r}_{2,\ldots
,}\vec{r}_{N}\right) \left( \hat{T}+\hat{V}_{ee}\right) \psi_{n\left(
\vec{r}\right) }\left( \vec{r}_{1},\vec{r}_{2,\ldots,}\vec{r}_{N}\right)
dr_{1}dr_{2}\ldots dr_{N} \quad(8)
および,
E_{LL}\left[ n\right] =F_{LL}\left[ n\right] +%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
v\left( \vec{r}\right) n\left( \vec{r}\right) d\vec{r} \quad(9)
を用いれば,$ n(\vec{r}) $が$ v $表示可能であろうがなかろうが,問題なくHohenberg-Kohnの第二定理の密度変分原理が成り立ち,$ n_{0}(\vec{r}) $を探索することができる,ということを示しました。ここで,$ (8) $式の$ \hat{T} $は運動エネルギー演算子, $ \hat{V}_{ee} $は電子間相互作用の演算子です。なお,$ (8) $式は,Levy-Liebの密度汎関数と呼ばれています。
さて,$ (8) $式および$ (9) $式の意味するところは,こういうことです。まず,電子密度$ n(\vec{r}) $を固定して,そのような特定の$ n(\vec{r}) $を与える多体波動関数$\psi_{n\left(\vec{r}\right)}\left(\vec{r}_{1},\vec{r}_{2,\ldots,}\vec{r}_{N}\right) $の組の中で,$ \hat{T} + \hat{V}_{ee} $の期待値を評価し,その値を最小化するような$\psi_{n\left(\vec{r}\right)}\left(\vec{r}_{1},\vec{r}_{2,\ldots,}\vec{r}_{N}\right) $を探します。そして,その最小値を$ F_{LL}[n] $($ (7) $式)と定義します。次に,今度は$ n(\vec{r}) $を固定せずに,$ (8) $式の左辺$ E_{LL}[n] $を最小化するような$ n(\vec{r}) $を探索します。つまり,最小化を二段階に分けて行います。このプロセスは,Levyの制限付き探索とよばれています。
Levyの制限付き探索は,次のように例えることができます。学校全体で一番背の高い生徒を見つける(=$ n_{0}(\vec{r}) $を探索する)のに,全員を校庭に一列に並ばせる必要はありません。単に,各教室で一番背の高い生徒を校庭に呼び出してから(=まず$ F_{LL}[n] $を決定する),背の高い順に一列に並べれば良いのです(=次に$ E_{LL}[n] $を最小化するような$ n(\vec{r}) $を探索して,$ n_{0}(\vec{r}) $を決定する)。
このような定式化で何が嬉しいのかというと,$ n(\vec{r}) $が$ v $表示可能な領域では,$ F_{LL}[n] $は,
F_{HK}\left[ n\right] =E_{HK}\left[ n\right] -%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
v\left( \vec{r}\right) n\left( \vec{r}\right) d\vec{r} \\
=F_{LL}\left[
n\right] \quad(10)
となることが分かり($ (10) $式の左辺をHohenberg-Kohnの「普遍的な」エネルギー汎関数と呼ぶこともあるようです。ここでの「普遍的な」という言葉の意味は,すべての電子系に対して同じであり,外部ポテンシャル$ v(\vec{r}) $とは無関係であるという意味です),また,$ n(\vec{r}) $が$ v $表示不可能な領域でも,汎関数$ F_{LL}[n] $が定義できる点です。この点が,$ (4) $式の,Hohenberg-Kohnの第二定理による$ n_{0}(\vec{r}) $の探索より優れていると言えるでしょう。前述のように,$ n(\vec{r}) $が$ v $表示可能であるための必要十分条件は知られていないので,Hohenberg-Kohnの定理は,現在では,Levyの制限付き探索と比較して,あまり重要な意味を持たない,と言われることさえあります(参考文献[6])。
ところで,$ (8) $式のLevy-Liebの密度汎関数は,$ \psi(\vec{r}_{1},\vec{r}_{2,\ldots,}\vec{r}_{N}) $から導かれるいかなる$ n(\vec{r}) $に対しても定義できます。これは$ N $表示可能性と呼ばれ,簡単な条件を満たすどのような$ n(\vec{r}) $に対しても,そのような$ \psi(\vec{r}_{1},\vec{r}_{2,\ldots,}\vec{r}_{N}) $が存在することはすでに分かっています(Harrimanの構成法,参考文献[7])。なおその条件($ n(\vec{r}) $が$ N $表示可能であるための必要十分条件)とは,
\begin{aligned}
& n\left( \vec{r}\right) \geq0 \quad(11) \\
& %
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
n\left( \vec{r}\right) d\vec{r}=N \quad(12) \\
& %
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
\left\vert \nabla n\left( \vec{r}\right) ^{\frac{1}{2}}\right\vert
^{2}d\vec{r}<\infty \quad(13)
\end{aligned}
です。$ (11) $式は,$ n(\vec{r}) $が非負である条件,$ (12) $式は,$ n(\vec{r}) $を全空間で積分すると系の全電子数Nに等しくなる条件,$ (13) $式は$ n(\vec{r}) $が十分になめらかな変化をするための条件です。いかにももっともな条件だと思います。また,上記の条件は$ n(\vec{r}) $が$ v $表示可能であるための必要条件であることも分かっています。つまり,$ N $表示可能性は$ v $表示可能性の必要条件となっているのです。
ここで,Hohenberg-Kohnの定理と比較したときの,Levyの制限付き探索のもう一つの利点を挙げることができます。すなわち,Levyの制限付き探索では,$ N $表示可能な$ n(\vec{r}) $を用いますが,個別の系で基底状態を求めたときに,(証明はされていませんが)$ v $表示可能な$ n_{0}(\vec{r}) $となっていることが期待されているのです(参考文献[8])。
ところで,「基底状態の電子密度$ n_{0}(\vec{r}) $が$ v $表示可能でない場合もあり得る」と書いたのに,「個別の系で基底状態を求めたときに,$ v $表示可能な$ n_{0}(\vec{r}) $となっていることが期待される」というのは,矛盾しているのではないかと思う方もいらっしゃると思いますが,実は私もそう思います。これは,私の中では密度汎関数理論の未解決問題の一つです。
最近,LLMとの対話で,外部ポテンシャル$ v $が与えられているのなら,それに対応する基底状態の電子密度$ n_{0}(\vec{r}) $は必ず$ v $表示可能(正確に言えばアンサンブル$ v $表示可能)であり,Levyの制限付き探索でこの電子密度に必ず到達できることを知りました。LLMのハルシネーションでなければ,これで長年の疑問は解決したことになります。
私の中での密度汎関数理論の未解決問題といえば,以下のような疑問もあります。そもそも密度汎関数理論は,3次元の関数である電子密度$ n(\vec{r}) $のみで,すべての議論が完結するのが「売り」ではなかったのでしょうか。しかし,$ (8) $式のLevy-Liebの密度汎関数では,結局,3N次元の多体波動関数$ \psi(\vec{r}_{1},\vec{r}_{2,\ldots,}\vec{r}_{N}) $の情報が必要となってしまっています。これでは,3N次元のSchrödinger方程式を,$ (7) $式の変分法で解くのとあまり変わらないのではないでしょうか。そもそも,$ n(\vec{r}) $から,$ \psi(\vec{r}_{1},\vec{r}_{2,\ldots,}\vec{r}_{N}) $を決定するには,どうすれば良いのでしょうか($ n(\vec{r}) $に対応するHamiltonian演算子$ \hat{H} $を求めてから、$ \psi(\vec{r}_{1},\vec{r}_{2,\ldots,}\vec{r}_{N}) $を求めるというのでは、密度汎関数理論の意味が全くないでしょう。なお、逆の問題は,$ (2) $式で既に示しました)。
これらの問題については,私も色々な本で調べたり,論文を漁ったりしてみましたが,解答は得られませんでした。ただ,現在の密度汎関数理論の標準的なスキームであるKohn-Sham法では,電子密度$ n(\vec{r}) $と同時に,3次元の関数である電子軌道(一電子波動関数のようなもの)も併用するので,先ほどの二つの疑問のうち後者の疑問は自然に氷解します(残念ながら,前者の疑問は残ったままです)。Kohn-Sham法については,後編にて詳しく論じたいと思います。
局所密度近似とThomas-Fermi(-Dirac)モデル
この節では,$ E_{HK}[n] $の近似式について述べていきたいと思います。$ E_{HK}[n] $の近似式を求めるに際して,まずは「同じ密度を持っている均質で一様な電子ガス」(一様電子ガス)を考えます。このような系では,$ E_{HK}[n] $は厳密に解析的に求めることができます(ただし,相関汎関数については,解析的に求めることができません。後編で詳しく解説します)。そして,実際に計算したい系も,「局所的には」一様電子ガスのように振る舞うと仮定します。これは,局所密度近似(Local Density Approximation, LDA)と呼ばれますが,この仮定,あるいは近似の妥当性については,以下でおいおい議論していきます。
さて,前述のように電子密度の汎関数としてのN電子系の全エネルギーは$ E_{HK}[n] $で与えられます。ここで,$ E_{HK}[n] $は,$ (10) $式から分かるように,二つの項に分解でき,
E_{HK}\left[ n\right] =F_{HK}\left[ n\right] +%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
v\left( \vec{r}\right) n\left( \vec{r}\right) d\vec{r} \quad(14)
となります。さらに,$ (8) $~$ (10) $式からの類推により,$ F_{HK}[n] $は三つの項に分解することができると考えられ,
F_{HK}\left[ n\right] =T\left[ n\right] +J\left[ n\right]
+E_{xc}\left[ n\right] \quad(15)
となります。ここで,$ T[n] $は運動エネルギー汎関数,$ J[n] $は古典的な電子-電子間のCoulomb相互作用によるエネルギーの汎関数(Hartreeエネルギーと呼ばれます),$ E_{xc}[n] $は量子力学的な(非古典的な)電子-電子間のCoulomb相互作用によるエネルギーの汎関数(交換相関エネルギーと呼ばれます。後編で詳しく解説します)です。ここで,厳密な表式が分かっているのは$ J[n] $のみであり,
J\left[ n\right] =\dfrac{1}{2}%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
\dfrac{n\left( \vec{r}\right) n\left( \vec{r}^{\prime}\right) }{\left\vert
\vec{r}-\vec{r}^{\prime}\right\vert }d\vec{r}d\vec{r}^{\prime} \quad(16)
と書けます。$ T[n] $と$ E_{xc}[n] $に対しては,前述のように厳密な表式が知られていません。従って,仕方がないので,これらの項に対してはLDAを適用します。すると,$ T[n] $と$ E_{xc}[n] $は
T\left[ n\right] \approx T_{TF}\left[ n\right] =\dfrac{3}{10}\left(
3\pi^{2}\right) ^{\frac{2}{3}}%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
n\left( \vec{r}\right) ^{\frac{5}{3}}d\vec{r} \quad(17)
および,
Exc\left[ n\right] \approx K_{D}\left[ n\right] =-\dfrac{3}{4}\left(
\dfrac{3}{\pi}\right) ^{\frac{1}{3}}%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
n\left( \vec{r}\right) ^{\frac{4}{3}}d\vec{r} \quad(18)
となります。ここで,$ T_{TF}[n] $は,Thomas-Fermiの運動エネルギー汎関数と呼ばれており,また,$ K_{D}[n] $は,Diracの交換エネルギー汎関数と呼ばれています(導出は例によって割愛します)。これらの式は,実はHohenberg-Kohnの定理が発表されるよりはるか以前から知られているものであり,$ T_{TF}[n] $が導かれたのは1927年,$ K[n] $が導かれたのは1928年のこと(Wikipediaのトーマス=フェルミ模型の記事より)です(なお,Schrödinger方程式が発表されたのは1926年のことです)。ところで,$ (14) $~$ (18) $式から,局所密度近似による(歴史的経緯からThomas-Fermi-Diracモデルと呼ばれることが多い)エネルギー汎関数$ E_{TFD}[n] $は,次式
E_{TFD}\left[ n\right] =C_{F}%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
n\left( \vec{r}\right) ^{\frac{5}{3}}+%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
v\left( \vec{r}\right) n\left( \vec{r}\right) d\vec{r}\mathbf{+}\dfrac
{1}{2}%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
\dfrac{n\left( \vec{r}\right) n\left( \vec{r}^{\prime}\right) }{\left\vert
\vec{r}-\vec{r}^{\prime}\right\vert }d\vec{r}d\vec{r}^{\prime}-C_{x}%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
n\left( \vec{r}\right) ^{\frac{4}{3}}d\vec{r} \quad(19)
となります。ここで,
\begin{aligned}
& C_{F}=\dfrac{3}{10}\left( 3\pi^{2}\right) ^{\frac{2}{3}} \quad (20) \\
& C_{x}=\dfrac{3}{4}\left( \dfrac{3}{\pi}\right) ^{\frac{1}{3}} \quad (21)
\end{aligned}
です。式$(19)$を見ると,電子密度$ n(\vec{r}) $だけの表式となっていることが分かります。この意味では,この式こそ密度汎関数理論のあるべき姿を最も簡潔に示したものと言えます。ここで,第一近似として右辺第4項を無視するならば,
E_{TF}\left[ n\right] =C_{F}%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
n\left( \vec{r}\right) ^{\frac{5}{3}}+%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
v\left( \vec{r}\right) n\left( \vec{r}\right) d\vec{r}\mathbf{+}\dfrac
{1}{2}%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
\dfrac{n\left( \vec{r}\right) n\left( \vec{r}^{\prime}\right) }{\left\vert
\vec{r}-\vec{r}^{\prime}\right\vert }d\vec{r}d\vec{r}^{\prime} \quad(22)
となりますが,これはThomas-Fermiモデルにおけるエネルギー汎関数$ E_{TF}[n] $と呼ばれています。
さてここで,原子に対する$ E_{TF}[n] $を考えてみましょう。原子では,
v\left( \vec{r}\right) =-\dfrac{Z}{r} \quad(23)
ですから(ここで$ Z $は原子番号です),これを$ (22) $式に代入すると,
E_{TF}\left[ n\right] =C_{F}%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
n\left( \vec{r}\right) ^{\frac{5}{3}}-%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
\dfrac{Z}{r}n\left( \vec{r}\right) d\vec{r}\mathbf{+}\dfrac{1}{2}%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
\dfrac{n\left( \vec{r}\right) n\left( \vec{r}^{\prime}\right) }{\left\vert
\vec{r}-\vec{r}^{\prime}\right\vert }d\vec{r}d\vec{r}^{\prime} \quad(24)
となります($ (1) $式と比べてみてください)。また,全電子数は$ Z $なので,
%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
n\left( \vec{r}\right) d\vec{r}=Z \quad (25)
が成り立ちます。ところで,$ (25) $式の制約条件の下での$ (24) $式の$ E_{TF}[n] $の停留条件は,(4)式と同様に,
\delta\left\{ E_{TF}\left[ n\right] -\mu_{TF}\left[
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
n\left( \vec{r}\right) d\vec{r}-N\right] \right\} =0 \quad (26)
となります。ここで,$ \mu_{TF} $はThomas-Fermiモデルにおける化学ポテンシャルです。$ (24) $式と$ (26) $式から,対応するEuler-Lagrange方程式
\mu_{TF}=\dfrac{5}{3}C_{F}n\left( \vec{r}\right) ^{\frac{2}{3}}-\phi\left(
\vec{r}\right) \quad(27)
が得られます。ここで,$ \phi(\vec{r}) $は,核および全電子の分布により生じた点$ \vec{r} $における古典的な静電ポテンシャルであり,
\phi\left( \vec{r}\right) =\dfrac{Z}{r}-%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
\dfrac{n\left( \vec{r}^{\prime}\right) }{\left\vert \vec{r}-\vec{r}^{\prime
}\right\vert }d\vec{r}^{\prime} \quad(28)
です。ここで,$ (27) $式を$ n(\vec{r}) $について解くと,
n\left( \vec{r}\right) =\left( \dfrac{3}{5C_{F}}\right) ^{\frac{3}{2}%
}\left[ \mu_{TF}+\phi\left( \vec{r}\right) \right] ^{\frac{3}{2}} \quad(29)
となります。さて,原子は核とそれに束縛された電子集団から成り立つ複合系という概念で捉えられるものです。したがって,この束縛された電子集団の電子密度$ n(\vec{r}) $は,$ r\rightarrow\infty $でゼロでなくてはなりません。しかも,この極限では,$ (28) $式から分かるように,$ \phi(\vec{r}) $もゼロにならなくてはならないので,結局,$ (29) $式が,$ r\rightarrow\infty $でも成立するための条件として,
\mu_{TF}=0 \quad(30)
が導かれます。従って,$ (29) $式は,
n\left( \vec{r}\right) =\left( \dfrac{3}{5C_{F}}\right) ^{\frac{3}{2}%
}\left[ \phi\left( \vec{r}\right) \right] ^{\frac{3}{2}} \quad(31)
となります。ここで,古典的な電磁気学のPoisson方程式をこの原子に適用すると,
\nabla^{2}\phi\left( \vec{r}\right) =4\pi n\left( \vec{r}\right) -4\pi
Z\delta\left( \vec{r}\right) \quad(32)
が得られます。さらに,$ (32) $式に,$ (31) $式を代入すると,
\nabla^{2}\phi\left( \vec{r}\right) =4\pi\left( \dfrac{3}{5C_{F}}\right)
^{\frac{3}{2}}\left[ \phi\left( \vec{r}\right) \right] ^{\frac{3}{2}}-4\pi
Z\delta\left( \vec{r}\right) \quad(33)
となります。ここで,この$ \phi(\vec{r}) $に対する境界条件としては,前述の,(1)$ r\rightarrow\infty $で$ r\phi(\vec{r})\rightarrow 0 $の他に,原子核近傍では核からのポテンシャルが支配的であるはずの要請から,(2)$ r\rightarrow0 $で,$ \phi(\vec{r})\rightarrow Z/r $という条件が課せられることになります。ところで,このような境界条件の下での微分方程式$ (33) $は,球対称な解しか持たないことが分かっているので,$ \phi(\vec{r}) $を
\phi\left( \vec{r}\right) \equiv\dfrac{Z}{r}y\left( x\right) \quad(34)
のように置き,$ x $だけの関数の形に書くことにします。ただし,
x=\alpha r,\alpha=Z^{\frac{1}{3}}\left( 4\pi\right) ^{\frac{2}{3}}\dfrac
{3}{5C_{F}}=\left( \dfrac{128}{9\pi^{2}}\right) ^{\frac{1}{3}}Z^{\frac{1}{3}} \quad(35)
です。$ (34) $式と$ (35) $式を,$ (33) $式に代入すると,最終的に,
\dfrac{d^{2}y\left( x\right) }{dx^{2}}=\dfrac{1}{\sqrt{x}}\left[ y\left(
x\right) \right] ^{\frac{3}{2}} \quad(36)
なる非線形常微分方程式が得られます。$ (36) $式は,Thomas-Fermi方程式と呼ばれています。ここで,$ y(x) $の境界条件は,前述の$ \phi(\vec{r}) $の境界条件を適宜読み替えることにより得られ,(1)$ y(\infty) = 0 $,および,(2)$ y(0) = 1 $となります。
$ (36) $式は,解析的には解けないので,数値的に解くことになります。著者は,$ (36) $式を有限要素法で解きましたが(このスライドとこのコード参照),いかんせんあまり精度が高くありませんでした。それでも,だいたいの傾向を掴むには十分なので,拙作のコードで$ (36) $式を解いた結果を載せたいと思います。
まず,$ y(x) $は,以下のプロットのような単調減少関数となります。
ここで,Thomas-Fermiモデルの電子密度$ n_{TF}(\vec{r}) $は,$ (31) $式,$ (34) $式および$ (35) $式から,
n_{TF}\left( \vec{r}\right) =\dfrac{32Z^{2}}{9\pi^{3}}\left[
\dfrac{y\left( x\right) }{x}\right] ^{\frac{3}{2}}=\dfrac{32Z^{2}}{9\pi
^{3}}\dfrac{y^{\prime\prime}\left( x\right) }{x} \quad(37)
となります。ここで,$ Z = 1 $(水素原子)として,$ n_{TF}(\vec{r}) $を図示すると,下図のようになります。
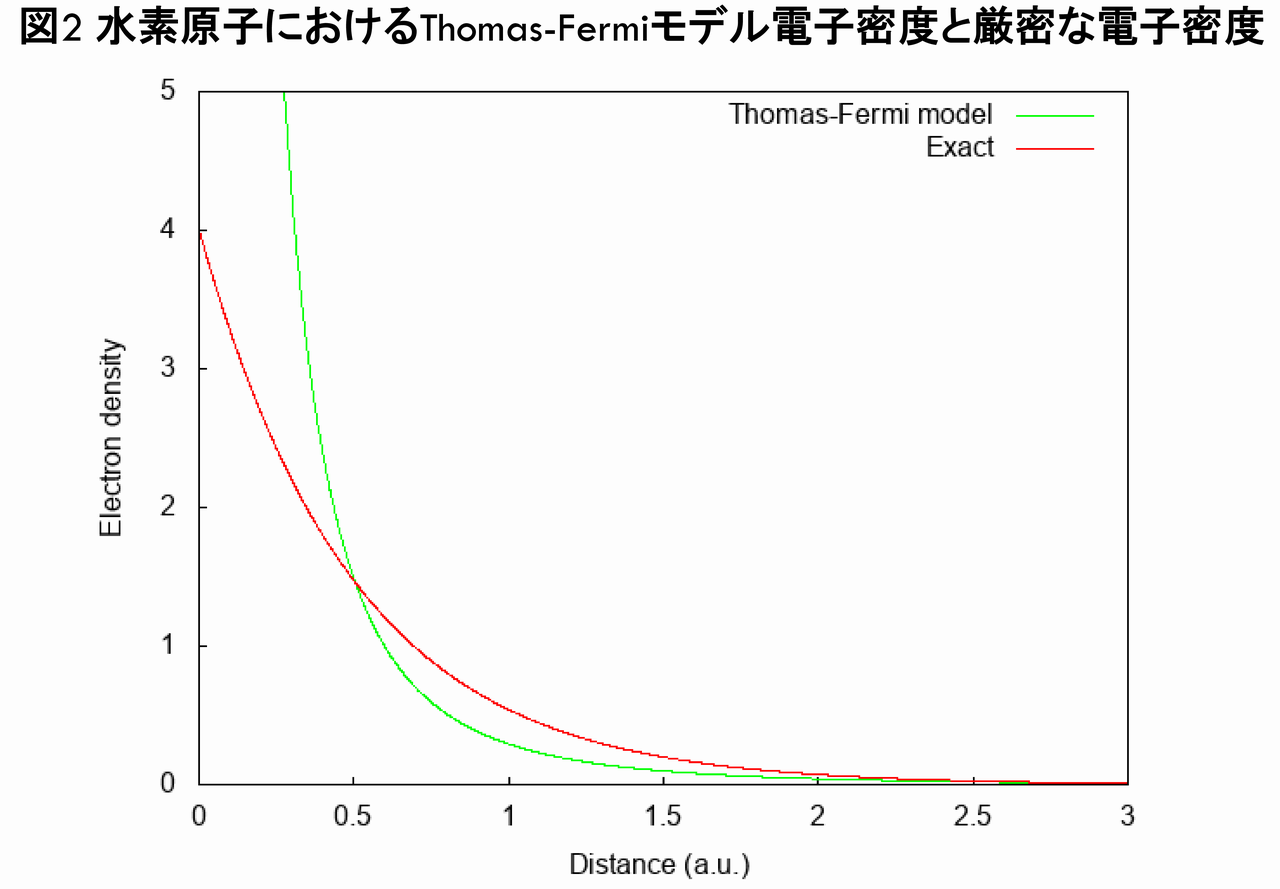
ここで,赤線は水素原子の厳密な密度$ n_{exact}(\vec{r}) $であり,Thomas-Fermiモデルの電子密度$ n_{TF}(\vec{r}) $(緑線)と比較しました。図2から分かるとおり,$ n_{TF}(\vec{r}) $は原点で発散してしまっており,$ n_{exact}(\vec{r}) $とは全く異なる,不正確な電子密度となっていることが分かります(実際,$ r\rightarrow0 $で,$ n_{TF}(\vec{r}) \propto r^{-3/2} $が導かれます)。次に,y軸を対数目盛にした場合の,$ n_{TF}(\vec{r}) $と$ n_{exact}(\vec{r}) $の比較は以下のグラフのようになります。
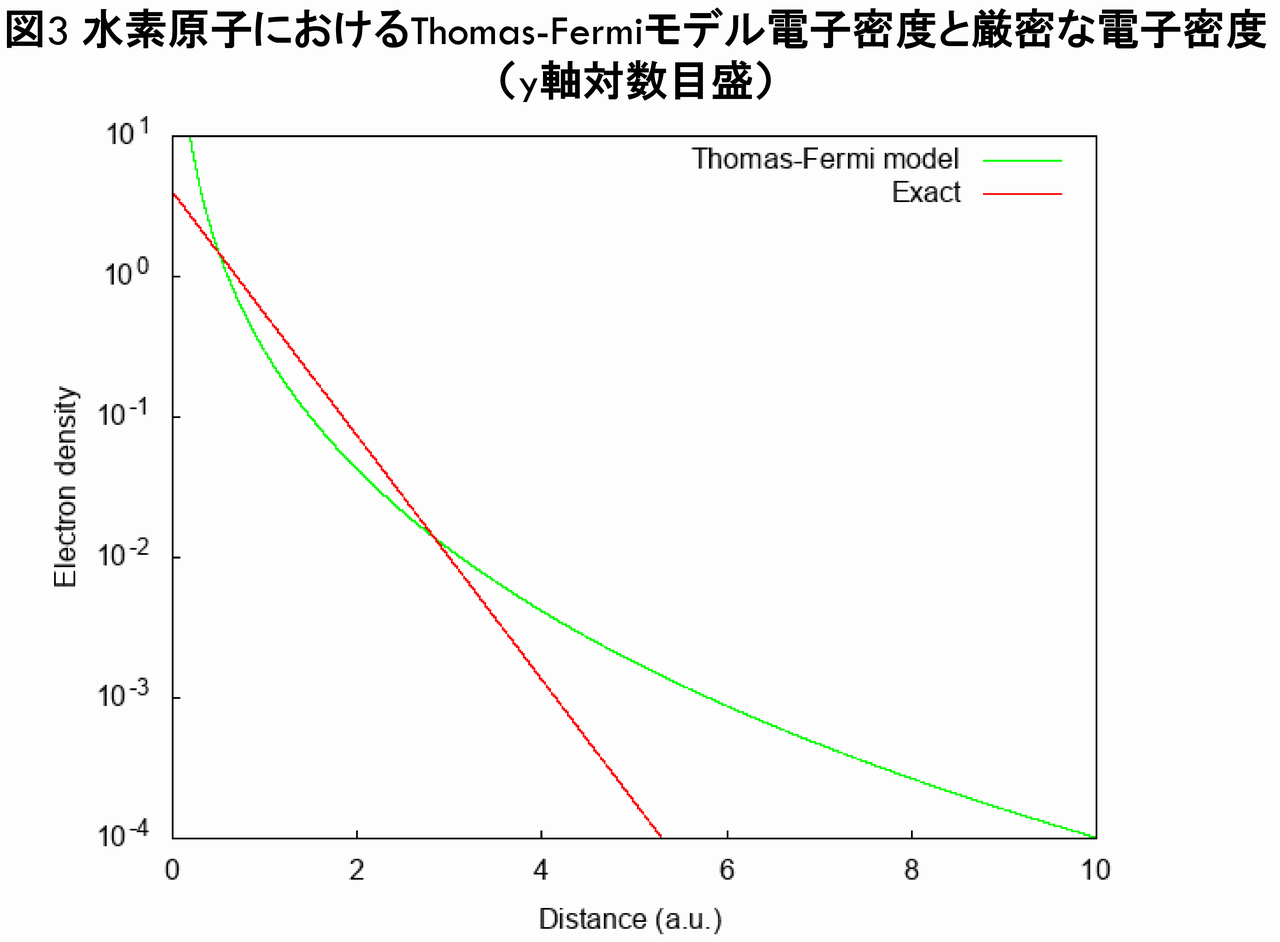
図3からも,$ n_{TF}(\vec{r}) $は$ n_{exact}(\vec{r}) $のように遠方で指数関数で減少しておらず,不正確な電子密度となっていることが分かります(実際,$ r\rightarrow\infty $で,$ n_{TF}(\vec{r}) \propto r^{-6} $が導かれます)。さらに,動径方向の電荷分布を表す$ r^{2}n(r) $を,$ n_{TF}(\vec{r}) $と$ n_{exact}(\vec{r}) $とで比較したグラフが下図です。
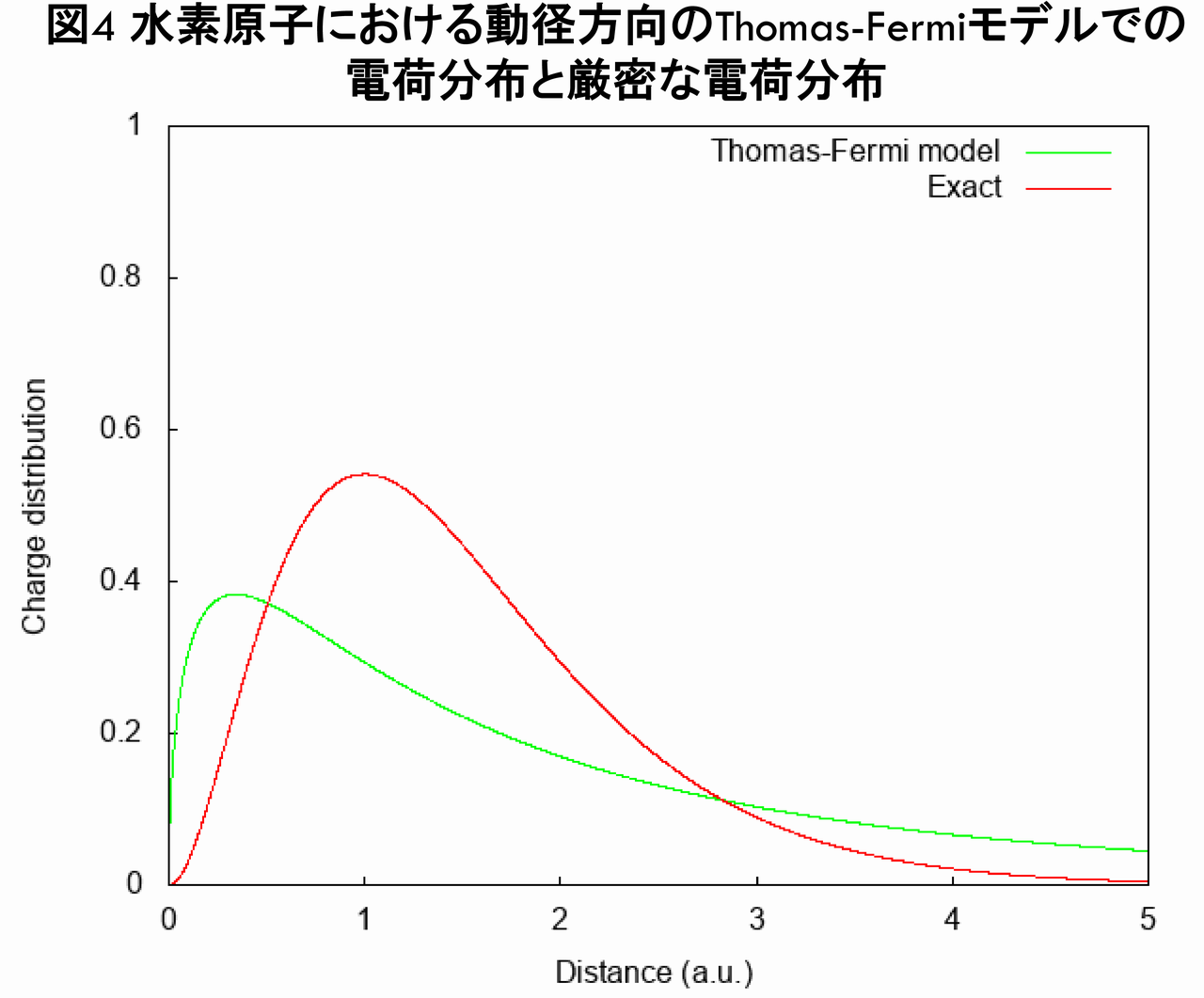
図4から分かるとおり,$ n_{TF}(\vec{r}) $は,$ n_{exact}(\vec{r}) $と全く似ていないことが分かります。また,この電荷分布を三次元プロットで比較したのが下図です。

図5から分かるとおり,Thomas-Fermiモデルの電荷分布の様子は,かなり三次元空間上に広がったものとなっており,図6の厳密な電荷分布の様子とは全く異なっていることが分かります(なお,電荷分布の三次元プロットには拙作のコードを用いました)。さらに,Thomas-Fermiモデルにおける原子の全エネルギーは,以下の式
E=-%
%TCIMACRO{\dint \nolimits_{0}^{Z}}%
%BeginExpansion
{\displaystyle\int\nolimits_{0}^{Z}}
%EndExpansion
dZ\left[
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
\dfrac{n_{TF}\left( \vec{r}\right) }{r}d\vec{r}\right] \quad(38)
で計算できます。ここで,$ (37) $式と,$ (38) $式から,
E=-4\pi%
%TCIMACRO{\dint \nolimits_{0}^{Z}}%
%BeginExpansion
{\displaystyle\int\nolimits_{0}^{Z}}
%EndExpansion
dZ%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
\dfrac{xn_{TF}\left( \vec{r}\right) }{\alpha^{2}}dx=-\dfrac{3}{7}%
\alpha\left[ y^{\prime}\left( \infty\right) -y^{\prime}\left( 0\right)
\right] Z^{\frac{7}{3}} \quad(39)
が得られ,これを数値的に計算すると,結局,
E=-0.7687Z^{\frac{7}{3}} \quad(40)
が得られます。$ (40) $式がThomas-Fermiモデルにおける原子のエネルギーです。これは,厳密な原子のエネルギーと比較すると,いずれの原子に対しても低すぎるエネルギー値を与えます。例えば,水素原子では54%,ヘリウム原子では33%,クリプトン原子では20%,そしてラドン原子では15%も低く出てしまう,といった具合です。ここで,鋭い方はもう気付いたかもしれませんが,厳密な原子のエネルギーより,Thomas-Fermiモデルによって計算された原子のエネルギーの方が値が常に低くなると言うことは,つまり変分原理が破れているらしいと言うことです。なぜかこの点について書かれた文献が見当たらないのですが,おそらくこれは,Thomas-Fermiモデルにおける原子の全エネルギー汎関数$ (24) $式が,変分原理を破るほど不正確であることを意味しているのだと思います。
さて,全エネルギーだけでなく,Thomas-Fermiモデルでは,決して説明出来ない実験事実がいくつもあることが知られています。たとえば,$ (37) $式で与えられるように,電子密度$ n(\vec{r}) $の$ Z $依存性が単に$ Z^2 $に比例しているのであれば,($ Z $の関数としてのある種の周期性の現れである)原子の周期表やそれの微視的起源である電子の殻構造の存在などは決して説明できません。また,$ (30) $式に示したように化学ポテンシャルが常にゼロであれば,原子にいくつかの電子を加えた負イオンは,(原子に電子を1つ加えるときには,その電子は少なくとも原子の化学ポテンシャル$ \mu $以上のエネルギー状態に置かなければなりませんが,$ \mu = 0 $なら,束縛状態に電子を置くことはできないから)決して安定束縛状態として存在し得ないということになりますが,これは$ H^- $イオンの存在を持ち出すまでもなく,事実に反することです。さらに,Thomas-Fermiモデルでは分子の形成を説明できないことも分かっています。
このように,Thomas-Fermiモデルでは化学や原子分子物理学の重要な多くの概念を定性的にすら説明できないので,大変不満足なものであることは明らかです。従って,これを改良するべく,Thomas-Fermiモデルを修正する試みが多数なされてきました。
真っ先に考えられるのは, $ (19) $式の$ E_{TFD}[n] $において,Diracの交換エネルギー汎関数$ K_{D}[n] $を無視して,$ (22) $式の$ E_{TF}[n] $を導いたのがまずかったのではないかという疑問です。しかし,Diracの交換エネルギー汎関数を無視せずに,Thomas-Fermi-Diracモデルによって原子のエネルギーを求めると,状況は改善されないばかりか,いっそう悪くなります。すなわち,$ K_{D}[n] $は正ですから,与えられた$ n(\vec{r}) $に対して,$ E_{TFD}[n] $は$ E_{TF}[n] $よりもさらに負の方向に大きくなります。さらに,$ E_{TFD}[n] $を$ n(\vec{r}) $について完全に最小化すると,エネルギーの値はもっと低くなってしまいます。
別の手段として,$ n_{TF}(\vec{r}) $は原点で発散していますが,これを原点で連続になるように改良する,という処方もあり,これは修正Thomas-Fermiモデルと呼ばれます。修正Thomas-Fermiモデルでは,もとのThomas-Fermiモデルよりずっともっともらしい原子の記述を与えますが,いぜんとして上記の問題は残ったままです。
さらに別の処方として,$ (24) $式第1項の運動エネルギー汎関数に何らかの補正をすることで,Thomas-Fermi(-Dirac)モデルを改良する,ということも考えられます。では,なぜ運動エネルギー汎関数を改良する必要があるのでしょうか。ここで,電荷分布をThomas-Fermiモデルと厳密なそれとで比較した図4を見ると,前者では電荷分布の主要部分が核に近づきすぎていることが分かります。つまり,もともと量子力学では核の引力ポテンシャルによる電子の局在化と,運動エネルギーによる電子の遍歴化という相反する二つの効果を折衷して電子状態が決定されているという原則から言えば,Thomas-Fermiモデルでは運動エネルギーの効果が十分に取り込まれておらず,引力ポテンシャルによる核への電子の吸引力が強すぎたということを意味しているのです。
さて,運動エネルギー汎関数を改良するには,LDAでは無視されている電子密度の非一様性を考慮する必要があります。具体的には,Thomas-Fermi(-Dirac)モデルの運動エネルギー汎関数に対して,密度勾配補正(Weizsacker補正)を加えて改良します。ここで,Thomas-Fermi(-Dirac)モデル運動エネルギーに対する密度勾配補正は,1粒子のGreen関数のWigner変換を半古典的に$ \hbar $展開することで得られます。密度勾配補正されたThomas-Fermi-Diracモデルは,Thomas-Fermi-Dirac-Weizsackerモデルと呼ばれますが,これはThomas-Fermi(-Dirac)モデルと比べると,修正Thomas-Fermiモデルと同様,ずっともっともらしい原子の記述を与えます。しかし,やはり上記の問題は残ったままです。では,Weizsacker補正(2次の密度勾配補正)より高次の密度勾配補正を行えば,より高い精度が得られるのではないかと思われるかもしれませんが,原子や分子の場合には,残念ながらこれが正しいのは4次までであり,6次の密度勾配補正は発散してしまいます。
従って,これらの処方で精度を上げることは,見たところほとんど不可能であり,代わりに現在では,専ら後編で詳細に述べる,Kohn-Sham法が使われています。ただし,「運動エネルギーに対して,正確な電子密度の汎関数を探す」という方針が,完全に放棄されたわけではないことには言及しておきたいと思います。事実,いくつかの研究室が,現在でもこの方針で研究を続けています(参考サイト[2])。この方針は,Orbital-free密度汎関数理論と呼ばれていますが,個人的には,これが上手く行くといいなと切に願っています。
さて,最初は前後編に分けるつもりはなかったのですが,非常に長くなったので,Kohn-Sham法の解説は後編の記事に回したいと思います。
参考サイト
[1] 量子力学/変分法 - 武内修@筑波大
[2] Orbital-free 密度汎関数理論における運動エネルギー汎関数の開発
[3] 「第一原理計算と密度汎関数理論」- 白井光雲
参考文献
[1] A. Tanaka, K. Maekawa, and K. Suzuki, Theoretical Calculations in Reaction
Mechanism Studies, Organic Synthesis Research Laboratory (2013).
[2] W. Zheng and L.-A. Ying, Int. J. Quant. Chem. 97, 659 (2004).
doi:10.1002/qua.10770
[3] P. Hohenberg and W. Kohn, Phys. Rev. 136, B864 (1964).
doi:10.1103/PhysRev.136.B864
[4] M. Levy, Proc. Natl. Acad. Sci. USA 76 6062 (1979).
doi:10.1073/pnas.76.12.6062
[5] E. H. Lieb, Int. J. Quant. Chem. 24, 243 (1983).
doi:10.1002/qua.560240302
[6] 高橋英明, 分子シミュレーション研究会会誌「アンサンブル」16(1) 51-54 (2014).
doi:10.11436/mssj.16.51
[7] J. E. Harriman, Phys. Rev. A. 24, 680 (1981).
doi:10.1103/PhysRevA.24.680
[8] 小田竜樹, 分子シミュレーション研究会会誌「アンサンブル」9(38) 40-44 (2008).
doi:10.11436/mssj1998.9.38_40
以下は全体的に参考にした文献です。
[9] R.G.パール, W.ヤング 『原子・分子の密度汎関数法』シュプリンガー・フェアラーク東京(1996)
[10] 高田康民 『多体問題特論―第一原理からの多電子問題 (朝倉物理学大系)』朝倉書店(2009)
[11] R.M.マーチン 『物質の電子状態 上』シュプリンガー・ジャパン株式会社(2010)