はじめに
この記事は,できるだけ簡単にHartree-Fock法を解説してみる(C++17のコード付き)(Physics Advent Calendar 2017 25日目)の記事の続きです。この記事では,前回の記事に引き続き、できる限り簡単(?)に、Hartree-Fock(ハートリー・フォック)法を解説していきます。
Hartree-Fock方程式とGTO(ガウス型軌道)による展開の特徴と問題
前回の記事では、Hartree-Fock法の方程式であるHartree-Fock方程式を基底で展開すると、Roothaan方程式と呼ばれる行列方程式が得られ、また展開の際に用いる基底には、専らGTOが用いられることを述べました。この記事ではまず、Hartree-Fock方程式をGTOで展開した際に生じる問題について述べ、次にHartree-Fock方程式そのものの特徴と問題について述べたいと思います。
GTOの問題
Hartree-Fock方程式をGTOで展開すると、STO(スレーター型軌道)で展開した場合に比べ、二つの問題が生じます。ヘリウム原子に対するHartree-Fock方程式を例にとって、このことを確認してみましょう。ヘリウム原子に対するHartree-Fock方程式を、1個のSTOのみで展開して解いた際の、波動関数$ \phi_{STO}\left( r\right) $と、n個のGTOの線形結合で展開して解いた際の波動関数$ \phi_{GTO}\left( r\right) $を比較すると、以下のグラフ(図1)のようになります(ヘリウム原子の系の対称性を思い出せば、波動関数が動径方向$ r $のみに依存する関数となり、なおかつ1番目の電子の(空間部分の)波動関数と、2番目の電子の(空間部分の)波動関数が等しくなることは明らかです。すなわち、$ \phi\left( \vec{r}_{1}\right) =\phi\left( \vec{r}_{2}\right) =\phi\left(r\right) $です)。
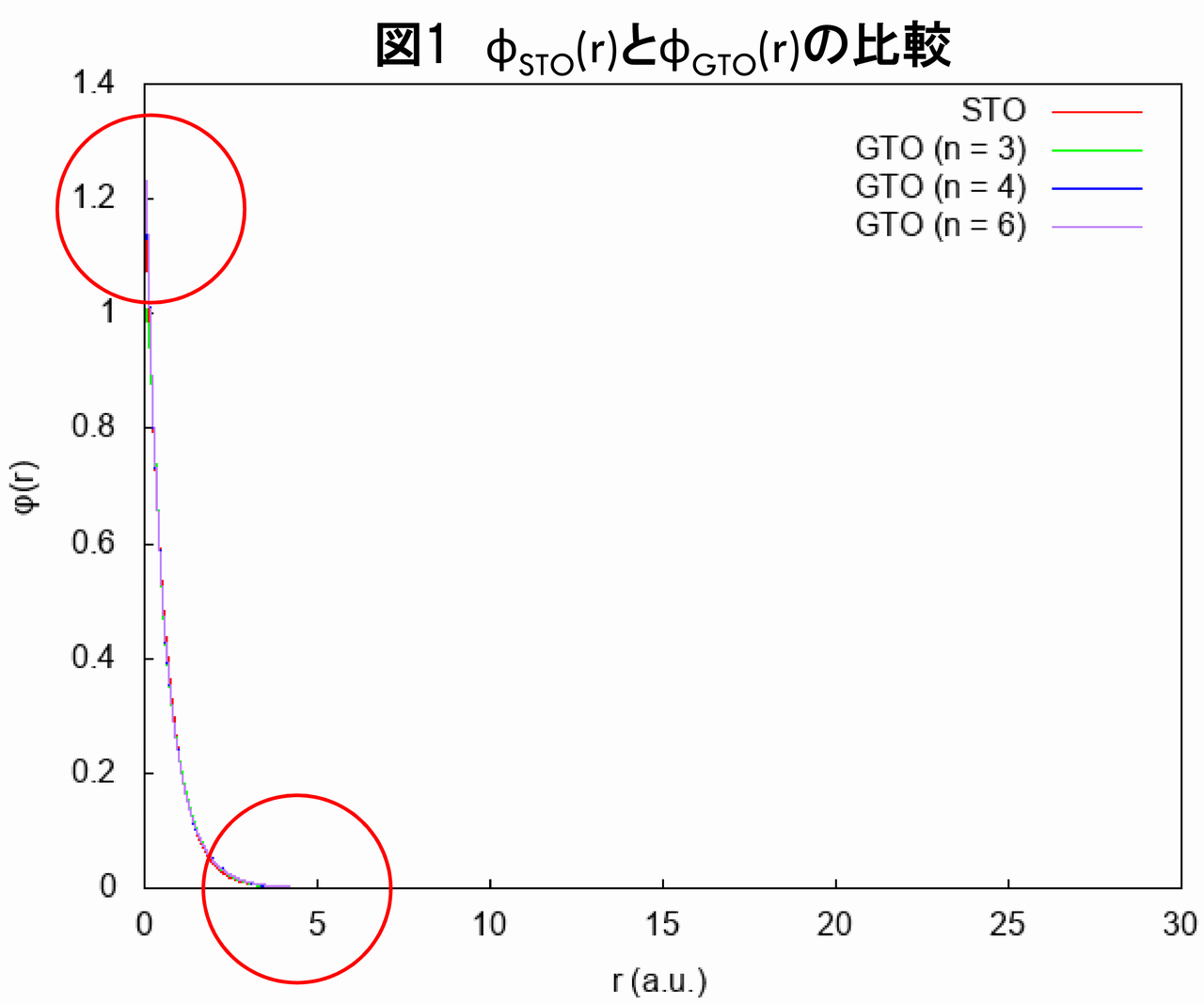
図1を見ると、$ \phi_{STO}\left( r\right) $と$ \phi_{GTO}\left( r\right) $とで、それほど差がないように見えます。しかし、実は両者は、核近傍と核から離れた遠方で、明らかに差があります。以下でこれを詳しく見ていきましょう。
核近傍におけるGTOの問題
核近傍における、GTOの問題を議論するため、図1を核近傍で拡大したグラフを以下に示します(図2)。
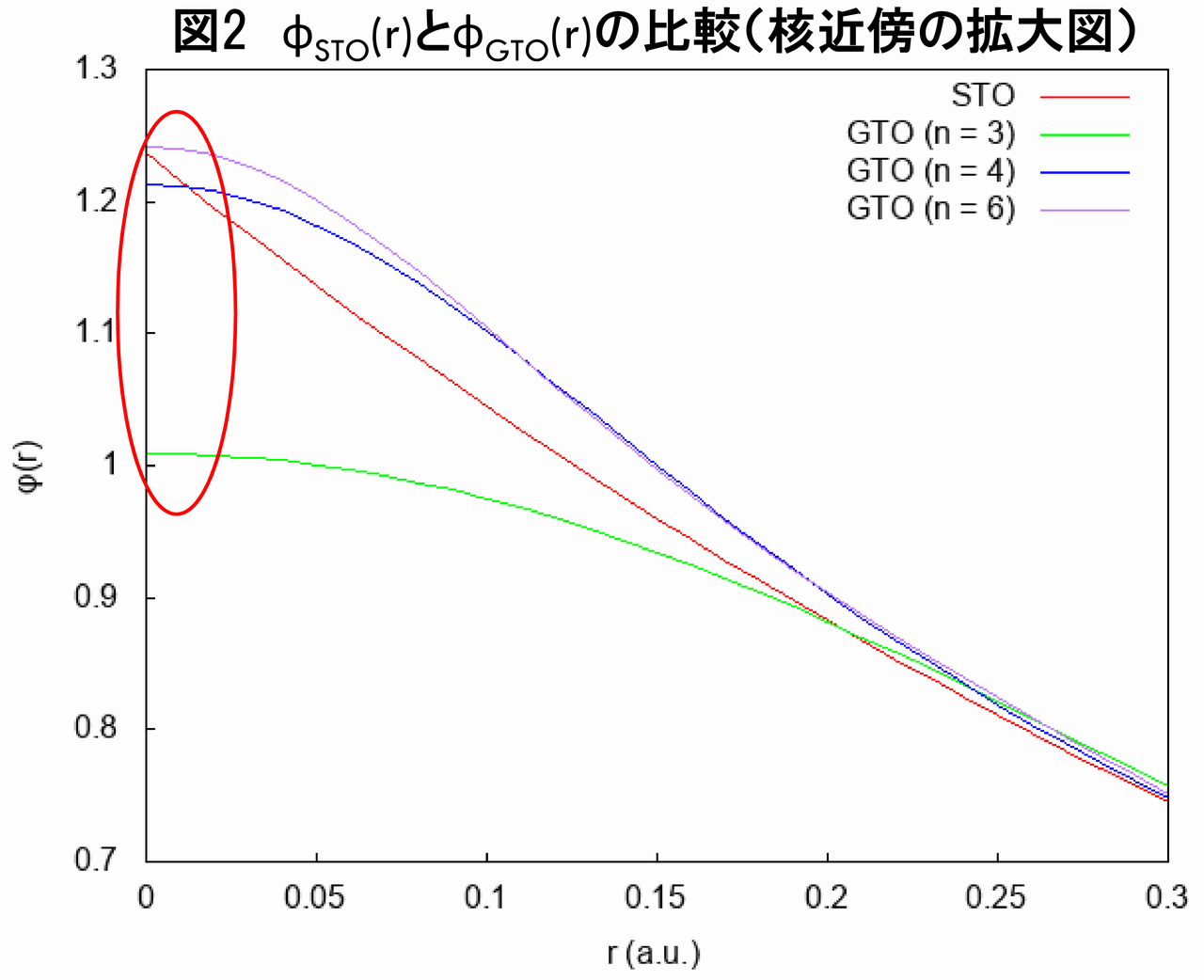
図2から分かるように、$ \phi_{STO}\left( r\right) $と比べて、$ \phi_{GTO}\left( r\right) $は核近傍で「丸まって」います。この理由は何なのでしょうか。これを理解するために、ヘリウム原子に対するHartree-Fock方程式をもう一度振り返ってみましょう。
\left[ -\dfrac{1}{2}\nabla_{1}^{2}-\dfrac{2}{r_{1}}+%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
d\vec{r}_{2}\left\vert \phi\left( \vec{r}_{2}\right) \right\vert ^{2}%
\dfrac{1}{\left\vert \vec{r}_{1}-\vec{r}_{2}\right\vert }\right] \phi\left(
\vec{r}_{1}\right) =E^{\prime}\phi\left( \vec{r}_{1}\right) \qquad(1)
$ (1) $式をよく見ると、原点(核の位置)で何やら変なことが起こっていることが分かります。すなわち、左辺括弧の中の第二項(Coulomb項)は、原点に極を持ちますが、一方で、右辺の$ \phi\left( \vec{r}_{1}\right) $は、原点に極を持っていてはなりません。なぜならば、$ \phi\left( \vec{r}_{1}\right) $は、Bornの確率解釈から、絶対値を二乗すると、電子の存在確率を表す関数となるはずだからです(もし、$ \phi\left( \vec{r}_{1}\right) $が、原点に極を持つような不連続な関数だったならば、核近傍に電子を見出す確率が無限大となってしまい、そのような関数は物理的に不適切です)。原点において、$ \phi\left( \vec{r}_{1}\right) $は連続であり、かつ左辺が発散しない、という、相反する二つの条件を満たすためには、原点での$ \phi\left( \vec{r}_{1}\right) $のラプラシアンが発散し、Coulomb項の発散を相殺していなければなりません。これは、核カスプ条件と呼ばれます。
ここで、STO、すなわち$ e^{-ar} $型の関数が、核カスプ条件を満たしていることを見てみましょう。球対称な系での、三次元極座標でのラプラシアンは、
\nabla^{2}=\dfrac{\partial^{2}}{\partial r^{2}}+\dfrac{2}{r}\dfrac{\partial
}{\partial r} \qquad(2)
です。$ (2) $式に、$ e^{-ar} $を作用させてみると、
\nabla^{2}e^{-ar}=\dfrac{\partial^{2}}{\partial r^{2}}e^{-ar}+\dfrac{2}{r}\dfrac{\partial}{\partial r}e^{-ar}=a^{2}e^{-ar}-\dfrac{2a}{r}e^{-ar} \qquad(3)
となり、確かに原点で発散していることが分かります。
一方、GTO、すなわちガウス関数$ e^{-ar^{2}} $を、$ (2) $式に作用させてみると、
\nabla^{2}e^{-ar^{2}}=\dfrac{\partial^{2}}{\partial r^{2}}e^{-ar^{2}}%
+\dfrac{2}{r}\dfrac{\partial}{\partial r}e^{-ar^{2}}=4a^{2}r^{2}e^{-ar^{2}%
}-6ae^{-ar^{2}} \qquad(4)
となり、これは原点で有限の値を持ちます(またGTOは、原点で極値を取るとは言うまでもありません)。つまり、GTOは核カスプ条件を満たしません。
上記の計算から、GTOはSTOに比べて、核近傍での物理的記述が不十分であることが分かります。これはあまり問題にされることはありませんが、GTOの欠点であることは間違いないでしょう。
核から離れた遠方におけるGTOの問題
次に、核から離れた遠方におけるGTOの問題を議論するため、図1のy軸対数プロットを以下に示します(図3)。
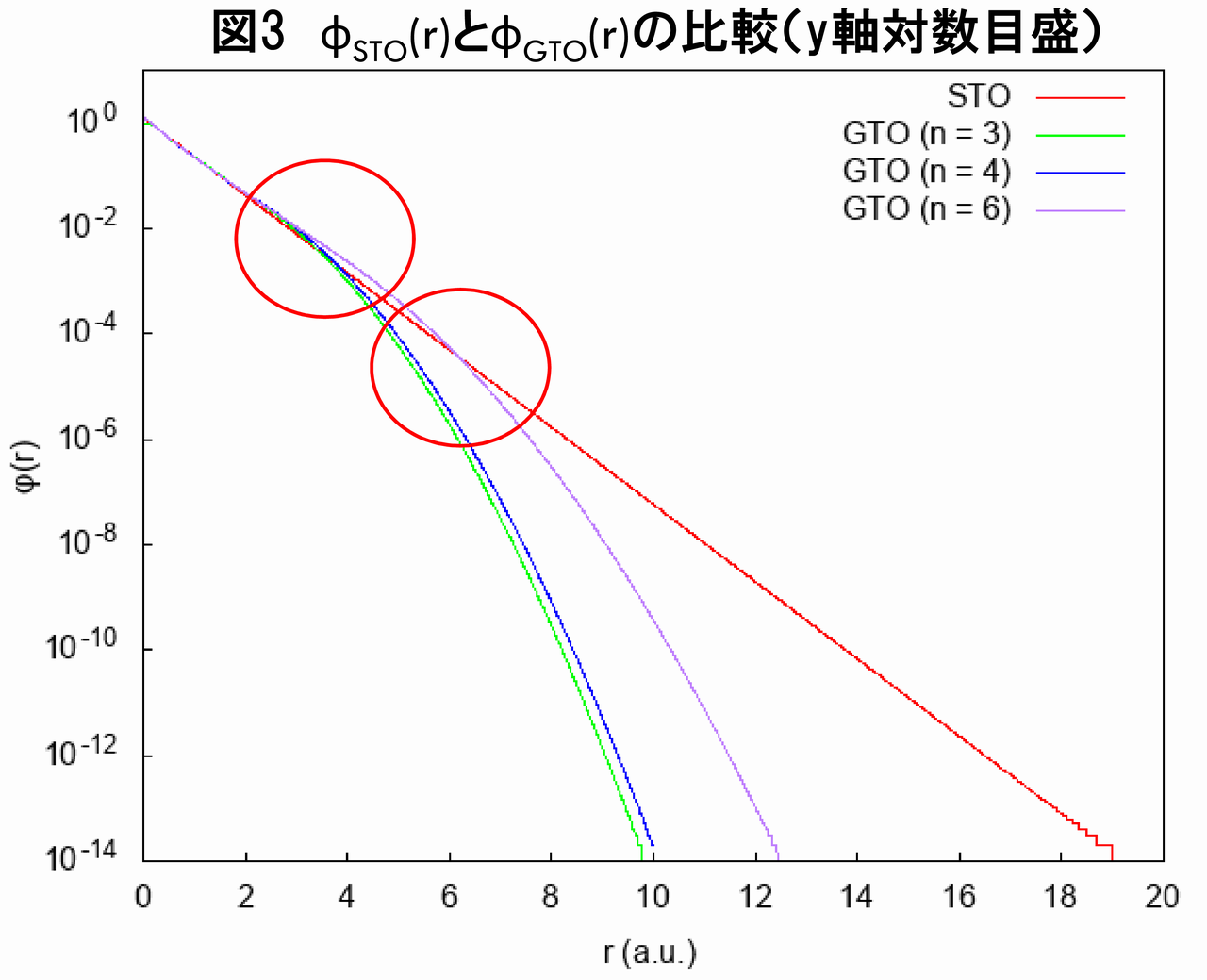
一般に、Hartree-Fock方程式における(1電子)波動関数は、核から離れた遠方で、指数関数で減衰する性質があることが知られています(参考文献[1])。STOがこの条件を満たすことは言うまでもありません。しかし、図3から分かるように、$ n = 3 $と$ n = 4 $のGTOは、$ r $が概ね4 (a.u.)より大きくなると、STOと比べて急激に減衰し、前述の条件を満たしません。また、$ n = 6 $のGTOは、$ n = 3 $や$ n = 4 $のそれよりかなり改善されますが、それでも$ r $が概ね7 (a.u.)より大きくなると指数関数より速く減衰し、やはり前述の条件を満たさないことが分かります。
上述のように、GTOはSTOに比べて、核から離れた遠方でも、物理的記述が不十分であることが分かります。核近傍におけるGTOの問題と同様に、この問題もGTOの欠点であることは論を俟たないのですが、取り上げられることはあまりありません。
Hartree-Fock法による特徴と問題
Hartree-Fock法には、大きな特徴と大きな問題が、それぞれ一つずつあります。以下でこれらについて詳しく説明します。
Hartree-Fock法の特徴-自己相互作用の相殺
前回の記事で、ヘリウム原子においては、Coulomb演算子$ J\left( \vec{r}_{1}\right) $と、交換演算子$ K\left(\vec{r}_{1}\right) $を(1電子)波動関数$ \phi\left( \vec{r}_{1}\right) $に作用させた結果が等しくなることを述べました。すなわち、
J\left( \vec{r}_{1}\right) \phi\left( \vec{r}_{1}\right) =K\left(
\vec{r}_{1}\right) \phi\left( \vec{r}_{1}\right) \qquad(5)
です。また、ヘリウム原子におけるCoulomb項は、
2J\left( \vec{r}_{1}\right) \phi\left( \vec{r}_{1}\right) =2%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
d\vec{r}_{2}\left\vert \phi\left( \vec{r}_{2}\right) \right\vert ^{2}%
\dfrac{1}{\left\vert \vec{r}_{1}-\vec{r}_{2}\right\vert }\phi\left( \vec
{r}_{1}\right) \qquad(6)
であり、交換項は、
K\left( \vec{r}_{1}\right) \phi\left( \vec{r}_{1}\right) =%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
d\vec{r}_{2}\left\vert \phi\left( \vec{r}_{2}\right) \right\vert ^{2}%
\dfrac{1}{\left\vert \vec{r}_{1}-\vec{r}_{2}\right\vert }\phi\left( \vec
{r}_{1}\right) \qquad(7)
ですから、Coulomb項が交換項のちょうど2倍となっていることも確認しました。これらはどういった意味があるのでしょうか。
結論から言うと、ヘリウム原子における交換項は、自分自身の軌道と相互作用する非物理的な項であり、Coulomb項の半分も、自分自身の軌道と総合作用する非物理的な項です(電磁気学などで学んだように、電子(電荷)は自分自身とは相互作用しません)。そして上手い具合に、両者がちょうど完全に相殺しています。この相殺は、ヘリウム原子に限らず、原子や分子の計算で一般に起こることであり、Hartree-Fock法の大きな特徴と言えます。一方で、次回か次々回で解説する予定の密度汎関数理論(Density Functional Theory、DFT)では、この相殺が完全ではなくなるため、重大な問題が引き起こされることが知られています。
Hartree-Fock法の問題-電子相関の欠如
Hartree-Fock法では、例えばヘリウム原子の場合、多電子波動関数$ \psi\left( \vec{x}_{1},\vec{x}_{2}\right) $を、
\psi\left( \vec{x}_{1},\vec{x}_{2}\right) =\phi\left( \vec{r}_{1}\right)
\phi\left( \vec{r}_{2}\right) \dfrac{1}{\sqrt{2}}\left[ \alpha\left(
s_{1}\right) \beta\left( s_{2}\right) -\alpha\left( s_{2}\right)
\beta\left( s_{1}\right) \right] \qquad(8)
と「変数分離」してしまう、と前回の記事で述べました。これは、かなり良い近似ではありますが、やはり代償を伴います。その代償が、電子相関です。電子相関によるエネルギー、すなわち相関エネルギーは、例えばヘリウム原子の場合、-0.0420 (Hartree)であり、これはヘリウム原子の精確なエネルギーである-2.9037 (Hartree)の、約1.4%に過ぎません。また、ヘリウム原子の精確な交換エネルギー(これは上述したように、全て自己相互作用によるものですが)である-1.0258 (Hartree)(この値は参考文献[2]より引用しました)と比べても、約4.1%に過ぎません。さらに、これは割合としてはむしろ大きい場合であり、ほとんどの場合、相関エネルギーは交換エネルギーの2~3%程度です。しかし、電子相関を無視することは、しばしば非物理的な結果をもたらします。例えば、次回で説明する予定の、水素分子の解離などはその顕著な例です。次節では、電子相関の欠如が、むしろ良い方向に作用している例について説明します。
Hartree-Fock法の特徴-Koopmansの定理
この節では、ヘリウム原子のイオン化エネルギーについて考えてみることにしましょう。ヘリウム原子の(第一)イオン化エネルギーは、
I=E\left( He^{+}\right) -E\left( He\right) \qquad(9)
です。ただし、右辺第一項はヘリウムイオンのエネルギー、第二項はヘリウム原子のエネルギーです。ここで、厳密に計算したヘリウム原子のエネルギ-の代わりに、Hartree-Fock法で計算したそれを使うことにしましょう。そうすると、$ (9) $式は以下のように書けます。
I\simeq E\left( He^{+}\right) -E_{HF}\left( He\right) \quad(10)
ただし、右辺第二項はHartree-Fock法で計算したヘリウム原子のエネルギーです。ここで、$ E\left( He^{+}\right) $は、1電子系なので、以下の式で書けるでしょう。
E\left( He^{+}\right) =%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
d\vec{r}_{1}\phi^{\ast}\left( \vec{r}_{1}\right) \left( \dfrac{1}{2}%
\nabla_{1}^{2}-\dfrac{2}{r_{1}}\right) \phi\left( \vec{r}_{1}\right) \qquad(11)
また、$ E_{HF}\left( He\right) $は、前回の記事で述べたように、以下の式で書けるでしょう。
E_{HF}\left( He\right) =%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
d\vec{r}_{1}\phi^{\ast}\left( \vec{r}_{1}\right) \left[ -\dfrac{1}{2}%
\nabla_{1}^{2}-\dfrac{2}{r_{1}}+%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
d\vec{r}_{2}\left\vert \phi\left( \vec{r}_{2}\right) \right\vert ^{2}%
\dfrac{1}{\left\vert \vec{r}_{1}-\vec{r}_{2}\right\vert }\right] \phi\left(
\vec{r}_{1}\right) + \\
%%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
d\vec{r}_{1}\phi^{\ast}\left( \vec{r}_{1}\right) \left( -\dfrac{1}{2}%
\nabla_{1}^{2}-\dfrac{2}{r_{1}}\right) \phi\left( \vec{r}_{1}\right) \qquad(12)
ただし、
%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
d\vec{r}_{1}\phi^{\ast}\left( \vec{r}_{1}\right) \left( -\dfrac{1}{2}%
\nabla_{1}^{2}-\dfrac{2}{r_{1}}\right) \phi\left( \vec{r}_{1}\right) =%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
d\vec{r}_{2}\phi^{\ast}\left( \vec{r}_{2}\right) \left( -\dfrac{1}{2}%
\nabla_{2}^{2}-\dfrac{2}{r_{2}}\right) \phi\left( \vec{r}_{2}\right) \qquad(13)
を使いました($ (13) $式はヘリウム原子の系の対称性から自明です)。ここで、$ (12) $式の右辺第一項は、$ (1) $式の軌道エネルギー$ E^{\prime} $と等しくなるはずですから、結局、$ (12) $式は、
E_{HF}\left( He\right) =E^{\prime}+%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
d\vec{r}_{1}\phi^{\ast}\left( \vec{r}_{1}\right) \left( -\dfrac{1}{2}%
\nabla_{1}^{2}-\dfrac{2}{r_{1}}\right) \phi\left( \vec{r}_{1}\right) \qquad(14)
となるでしょう。従って、イオン化エネルギー$ I $は結局、$ (11) $式と$ (14) $式から、
I\simeq%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
d\vec{r}_{1}\phi^{\ast}\left( \vec{r}_{1}\right) \left( \dfrac{1}{2}%
\nabla_{1}^{2}-\dfrac{2}{r_{1}}\right) \phi\left( \vec{r}_{1}\right)
-\left[ E^{\prime}+%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
d\vec{r}_{1}\phi^{\ast}\left( \vec{r}_{1}\right) \left( -\dfrac{1}{2}%
\nabla_{1}^{2}-\dfrac{2}{r_{1}}\right) \phi\left( \vec{r}_{1}\right)
\right] =-E^{\prime} \qquad(15)
となります。つまり、イオン化エネルギー$ I $は、$ (1) $式の軌道エネルギー$ E^{\prime} $の符号を逆転したものに等しいのです。実際に、前回の記事で紹介したプログラムによる$ n = 3 $、$ n = 4$、$ n = 6 $のときの軌道エネルギー$ E^{\prime} $の計算結果(の絶対値)と、実験によるイオン化エネルギー(この値は参考サイト[1]から引用しました)を比較した表を、以下に示します。
| n | 軌道エネルギーの絶対値 (Hartree) |
|---|---|
| 3 | 0.8976 |
| 4 | 0.9142 |
| 6 | 0.9172 |
| 実験 | 0.9036 |
上図のように、実験によるイオン化エネルギーと、Hartree-Fock法による計算との誤差は、$ n = 3 $、$ n = 4$、$ n = 6 $のときのいずれも、1%程度となっており、非常に良い結果となっています。この、「(第一)イオン化エネルギー$ I $は、Hartree-Fock方程式の軌道エネルギー$ \epsilon $の符号を逆転したものに等しい」という法則は、ヘリウム原子だけでなく、Hartree-Fock法で一般の原子や分子を計算したときに広く成り立つので、Koopmans(クープマンズ)の定理と呼ばれています(この定理は、T. C. Koopmansによって、1934年に示されました(参考サイト[2])。余談ですが、T. C. Koopmansは、後に経済学に転向し、1975年にはノーベル経済学賞を受賞しました)。
しかし、実際にはこれは定理ではありません。と言うのも、この「定理」は、二つの要因による誤差がうまく打ち消し合った結果だからです。
誤差の第一の要因は、電子相関を無視していることです。前述のように、厳密な$ E\left( He\right) $は、電子相関の効果によって$ E_{HF}\left( He\right) $より-0.0420 (Hartree)だけ、マイナスの方向に大きくなっています。
誤差の第二の要因は、電子の緩和効果を無視していることです。すなわち、ヘリウム原子から電子が引き抜かれてヘリウムイオンになったとき、残された一つの電子は、引き抜かれた電子による遮蔽効果がなくなるため、ヘリウム原子の時よりも核により近づくことができます。従って、ヘリウム原子の$ \phi\left( \vec{r}_{1}\right) $と、ヘリウムイオンの$ \phi\left( \vec{r}_{1}\right) $とは、異なった関数になります。$ (11) $式では、ヘリウム原子の$ \phi\left( \vec{r}_{1}\right) $を用いて、$ E\left( He^{+}\right)$を評価していますが、つまるところこれは厳密な$ E\left( He^{+}\right)$ではないのです。実際、計算してみると、ヘリウム原子の$ \phi\left( \vec{r}_{1}\right) $を用いた$ E\left( He^{+}\right)$と、厳密な$ E\left( He^{+}\right)$では、後者の方が-0.0590 (Hartree) だけ(ただし、$ n = 4 $あるいは$ n = 6 $の場合)、マイナスの方向に大きいことが分かります。
軌道エネルギーが、イオン化エネルギーの第一近似として妥当な値を与えるのは、この二つの要因による誤差が、上手い具合に相殺してくれるからです。それゆえ、「定理」が成り立っているように見えます。一方、電子親和力の場合は、上述の二つの要因による誤差が相殺せず、逆に累積するため、軌道エネルギーが電子親和力の良好な近似となることは少ないことが知られています(それどころか、定性的に誤った結果を与えることすらあります)。
まとめ
Hartree-Fock方程式をGTOで展開した際に、核近傍と核から離れた遠点で生じる問題について述べました。また、Hartree-Fock法における特徴である自己相互作用と、Hartree-Fock法における問題である電子相関の欠如について述べました。最後に、電子相関の欠如の、いわば怪我の功名の結果として得られる「定理」である、Koopmansの定理について述べました。
参考サイト
[1] イオン化エネルギー - Wikipedia
[2] Koopmans' theorem - Wikipedia
参考文献
[1] R.G.パール, W.ヤング 『原子・分子の密度汎関数法』シュプリンガー・フェアラーク東京(1996)
[2] R.M.マーチン 『物質の電子状態 上』シュプリンガー・ジャパン株式会社(2010)