局所密度近似（LDA）でヘリウム原子のエネルギーを計算してみる（C++17のソースコード付き）

この記事では，LDA汎関数（Dirac-Slaterの交換汎関数（参考文献[1]，参考文献[2]）とVWN相関汎関数（参考文献[3]）の組み合わせ）を用いて，Kohn-Sham方程式を解き，この記事の$ (1) $式の右辺の$ E $を計算してみることにします。なお，Kohn-Sham方程式そのものについてはこちらの記事で，また水素原子に対するKohn-Sham方程式については，こちらの記事で解説しています。

#ヘリウム原子に対するKohn-Sham方程式
さて，早速ですが，ヘリウム原子に対するKohn-Sham方程式は，LDA-VWN汎関数を用いた場合，Hartree原子単位系で（以下，断りなしにHartree原子単位系を用いることとします），

\left[  -\dfrac{1}{2}\nabla^{2}-\dfrac{2}{r}+2%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
d\vec{r}^{\prime}\left\vert \phi\left(  \vec{r}^{\prime}\right)  \right\vert
^{2}\dfrac{1}{\left\vert \vec{r}-\vec{r}^{\prime}\right\vert }-\left(
\dfrac{3}{\pi}\right)  ^{\frac{1}{3}}n\left(  \vec{r}\right)  ^{\frac{1}{3}%
}+v_{c}^{VWN}\left(  \vec{r}\right)  \right]  \phi\left(  \vec{r}\right)
=E^{\prime}\phi\left(  \vec{r}\right) \quad(1)

となります。ただし，

n\left(  \vec{r}\right)  =2\left\vert \phi\left(  \vec{r}\right)  \right\vert
^{2} \quad(2)

です。ここで，$ (1) $式の左辺括弧の中の第3項はHartreeポテンシャル，第4項はLDA交換ポテンシャル，左辺括弧の中の第5項はVWN相関ポテンシャルです。ここで，$ (1) $式を，この記事の $ (7) $式と比較すると，左辺括弧の中のHartreeポテンシャル項が2倍になり，また左辺第4項，左辺第5項が増えていることが分かります。
ここで，Hartreeポテンシャル項が，この記事の $ (7) $式のちょうど2倍になることの理由は，この記事で説明しました。つまり，元々Hartreeポテンシャルには，自分自身と相互作用する非物理的な項が含まれており，ヘリウム原子の場合，それはHartreeポテンシャルのちょうど半分を占めます。ところが，Hartree-Fock法の場合，交換ポテンシャルにも自分自身と相互作用する項が存在していて，かつHartreeポテンシャルの自分自身と相互作用する項と，交換ポテンシャルの自分自身と相互作用する項がちょうど相殺してくれているのです。従って，この記事の$ (7) $式のHartreeポテンシャルは，元々の分から自分自身と相互作用する分を差し引いた，物理的に正しい量になっているというわけです（そして，自分自身と相互作用する非物理的な交換ポテンシャルは，完全に消えてくれています）。
さて，LDA-VWN交換相関汎関数を用いたKohn-Sham法では，LDA交換ポテンシャルは，この記事の$ (18) $式とこの記事の$ (13) $式から，

v_{x}^{LDA}\left(  \vec{r}\right)  =\left(  \dfrac{3}{\pi}\right)  ^{\frac
{1}{3}}n\left(  \vec{r}\right)  ^{\frac{1}{3}} \quad(3)

となります（この式は，$ (1) $式ですでに出しました）。ここで，Kohn-Sham法でもHartreeポテンシャルについて，Hartree-Fock法と同様のことが期待できるでしょうか。結論から言うと，「Kohn-Sham法では，Hartreeポテンシャルの自分自身と相互作用する非物理的な項は，完全には消えてくれない」です。これは自己相互作用問題と呼ばれています。さて，$ (3) $式に対応するLDA交換エネルギーは，この記事の$ (18) $式から，

E_{x}^{LDA}\left[  n\right]  =-\dfrac{3}{4}\left(  \dfrac{3}{\pi}\right)
^{\frac{1}{3}}n\left(  \vec{r}\right)  ^{\frac{4}{3}} \quad(4)

となります。従って，ヘリウム原子のエネルギーは，この記事の$ (8) $式および$ (14) $式から，

E=2E^{\prime}-\dfrac{1}{2}%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
\dfrac{n\left(  \vec{r}\right)  n\left(  \vec{r}^{\prime}\right)  }{\left\vert
\vec{r}-\vec{r}^{\prime}\right\vert }d\vec{r}d\vec{r}^{\prime}+%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
\left\{  -\dfrac{3}{4}\left(  \dfrac{3}{\pi}\right)  ^{\frac{1}{3}}n\left(
\vec{r}\right)  ^{\frac{4}{3}}d\vec{r}+\epsilon_{c}^{VWN}\left(  \left[
n\right]  ,\vec{r}\right)  \right\}  n\left(  \vec{r}\right)  d\vec{r}-%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
\left[  -\left(  \dfrac{3}{\pi}\right)  ^{\frac{1}{3}}n\left(  \vec{r}\right)
^{\frac{1}{3}}+v_{c}^{VWN}\left(  \vec{r}\right)  \right]  n\left(  \vec
{r}\right)  d\vec{r} \quad(5)

となります（$ E^{\prime} $が2倍されているのは，空間軌道$ \phi $に，2個の電子が詰まっているからです）。ここで，$ \epsilon_{c}^{VWN}\left( \left[ n\right] ,\vec{r}\right) $（あるいは$v_{c}^{VWN}(\vec{r}) $も）は，本来であれば二種類のスピン密度$ n^{\alpha}(\vec{r}) $および$ n^{\beta}(\vec{r}) $の両方に依存するのですが，ヘリウム原子は閉殻系でスピン分極していないので，単に，

n^{\alpha}\left(  \vec{r}\right)  =n^{\beta}\left(  \vec{r}\right)
=\dfrac{n\left(  \vec{r}\right)  }{2} \quad(6)

とすれば済みます（なお一般の場合には，$ \alpha $スピンと$ \beta $スピンの各々に対して，別々にKohn-Sham方程式を解いて，これらを連立させなければなりません）。なお一般に，LDA-VWNの相関エネルギー汎関数，および相関ポテンシャル汎関数の式は非常に複雑なので，ここでは紹介しません。
さてここで，この記事で行ったように，

\phi\left(  \vec{r}\right)  =%
%TCIMACRO{\dsum \limits_{p=1}^{n}}%
%BeginExpansion
{\displaystyle\sum\limits_{p=1}^{n}}
%EndExpansion
C_{p}\chi_{p}\left(  \vec{r}\right) \quad(7)

なる$ n $個の基底を用いて，$ (1) $式を展開し，かつ左から$ \chi_{p}(\vec{r}) $を乗じ，$ \vec{r} $について全空間で積分すると，

F_{pq}=h_{pq}+2%
%TCIMACRO{\dsum \limits_{r,s=1}^{n}}%
%BeginExpansion
{\displaystyle\sum\limits_{r,s=1}^{n}}
%EndExpansion
C_{r}C_{s}Q_{prqs}+K_{pq} \quad(8)

および

\mathbf{F}\vec{C}=E^{\prime}\mathbf{S}\vec{C} \quad(9)

なる，一般化固有値問題が得られます。ただし，

h_{pq}=%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
d\vec{r}\chi_{p}\left(  \vec{r}\right)  \left(  -\dfrac{1}{2}\nabla
_{1}^{2}-\dfrac{2}{r_{1}}\right)  \chi_{q}\left(  \vec{r}\right) \quad(10) \\

Q_{prqs}=%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
d\vec{r}d\vec{r}^{\prime}\chi_{p}\left(  \vec{r}\right)  \chi_{r}\left(
\vec{r}^{\prime}\right)  \dfrac{1}{\left\vert \vec{r}-\vec{r}^{\prime
}\right\vert }\chi_{q}\left(  \vec{r}\right)  \chi_{s}\left(  \vec{r}^{\prime
}\right) \quad(11) \\

K_{pq}=%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
d\vec{r}\chi_{p}\left(  \vec{r}\right)  \left[  -\left(  \dfrac{3}{\pi
}\right)  ^{\frac{1}{3}}n\left(  \vec{r}\right)  ^{\frac{1}{3}}+v_{c}%
^{VWN}\left(  \vec{r}\right)  \right]  \chi_{q}\left(  \vec{r}\right) \quad(12) \\

S_{pq}=%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
d\vec{r}\chi_{p}\left(  \vec{r}\right)  \chi_{q}\left(  \vec{r}\right) \quad(13)

です。なお，$ (10) $式は1電子積分，$ (11) $式はCoulomb積分，$ (13) $式は重なり積分と呼ばれます。また，$ (12) $式は，交換相関積分と呼ぶことにします。複雑そうに見えますが，やっていることは，この記事で解説したことと全く同じです）。後は$ (9) $式を数値的に解くだけです。
ここで，基底にGTOを用いると，基底状態については，$ l = 0 $の関数（s関数）だけが必要であり，これは，原子核に中心がある（そのためそこを原点に置く）ので，$ \chi_{p}(\vec{r}) $は，以下のようになります。

\chi_{p}(\vec{r})  =e^{-\alpha_{p}r^{2}} \quad(14)

$ (14) $式を用いると，ヘリウム原子における，1電子積分$ h_{pq} $とCoulomb積分$ Q_{prqs} $，および重なり積分$ S_{pq} $は，解析的に求められます（計算結果は，この記事に記載してあるので，ここでは省略します）。ただし，$ (12) $式の交換相関積分$ K_{pq} $だけは，以下の式によって，数値的に求めなければなりません。

K_{pq}=4\pi%
%TCIMACRO{\dint _{0}^{\infty}}%
%BeginExpansion
{\displaystyle\int_{0}^{\infty}}
%EndExpansion
r^{2}\chi_{p}\left(  r\right)  \left[  -\left(  \dfrac{3}{\pi}\right)
^{\frac{1}{3}}n\left(  r\right)  ^{\frac{1}{3}}+v_{c}^{VWN}\left(  r\right)
\right]  \chi_{q}\left(  r\right)  dr \quad(15)

ここで，具体的な$ \alpha_{p} $の値についてですが，この記事に，$ n = 4 $の場合の値を記載しましたので，ここでは省略します。さてこれで，行列要素を埋めるための情報が全て得られましたので，以下の手続きに従って，$ (9) $式を自己無撞着に解くだけです。

1. 固有ベクトル$ \vec{C} $の要素$ C_{p} $の初期値を適当に選びます。これは例えば，全部$ 1 $とかで構いません（今はヘリウム原子という単純な系を考えているので，たいていの初期値から正しい解に収束するはずです。ただ，全部0だけはダメです）。また，重なり行列$ \mathbf{S} $も計算しておきます。
2. 固有ベクトル$ \vec{C} $を，

\vec{C}:=\dfrac{1}{\sqrt{4\pi%
%TCIMACRO{\dsum \limits_{p=1}^{n}}%
%BeginExpansion
{\displaystyle\sum\limits_{p=1}^{n}}
%EndExpansion%
%TCIMACRO{\dsum \limits_{q=1}^{n}}%
%BeginExpansion
{\displaystyle\sum\limits_{q=1}^{n}}
%EndExpansion
C_{p}C_{q}%
%TCIMACRO{\dint _{0}^{\infty}}%
%BeginExpansion
{\displaystyle\int_{0}^{\infty}}
%EndExpansion
r^{2}\chi_{p}\left(  r\right)  \chi_{q}\left(  r\right)  dr}}\vec{C} \quad(16)

とすることにより，Kohn-Sham固有関数を正規化します。
3. 電子密度$ n(r) $を，

n\left(  r\right)  =2\left[
%TCIMACRO{\dsum \limits_{p=1}^{n}}%
%BeginExpansion
{\displaystyle\sum\limits_{p=1}^{n}}
%EndExpansion
C_{p}\chi_{p}\left(  r\right)  \right]  ^{2} \quad(17)

により求めます。
4. ステップ2で求めた固有ベクトル$ \vec{C} $と，ステップ3で求めた電子密度$ n(r) $から，$ (8) $式によって，Fock行列$ \mathbf{F} $を計算します。
5. $ (8) $式の一般化固有値問題を数値的に解きます。
6. エネルギー$ E $を，

E=2E^{\prime}-2%
%TCIMACRO{\dsum \limits_{p,q,r,s=1}^{m}}%
%BeginExpansion
{\displaystyle\sum\limits_{p,q,r,s=1}^{m}}
%EndExpansion
C_{p}C_{q}C_{r}C_{s}Q_{prqs}+K^{\prime}-2%
%TCIMACRO{\dsum \limits_{p,q=1}^{n}}%
%BeginExpansion
{\displaystyle\sum\limits_{p,q=1}^{n}}
%EndExpansion
K_{pq} \quad(18)

により求めます。ここで，$ K^{\prime} $は，

K^{\prime}=4\pi%
%TCIMACRO{\dint _{0}^{\infty}}%
%BeginExpansion
{\displaystyle\int_{0}^{\infty}}
%EndExpansion
r^{2}\left[  -\dfrac{3}{4}\left(  \dfrac{3}{\pi}\right)  ^{\frac{1}{3}%
}n\left(  \vec{r}\right)  ^{\frac{4}{3}}d\vec{r}+\epsilon_{c}^{VWN}\left(
\left[  n\right]  ,\vec{r}\right)  \right]  n\left(  r\right)  dr \quad(19)

で定義されますが，これは数値的に求めなければなりません。
7. ステップ5で求まった固有ベクトル$ \vec{C} $から，電子密度$ n(r) $を$ (17) $式によって求め，これらから，Fock行列$ \mathbf{F} $を計算します。
8. ステップ5～7を，前回計算したエネルギー$ E_{old} $と，今回計算したエネルギー$ E_{new} $の差の絶対値$ \left\vert E_{new}-E_{old}\right\vert $が，ある閾値未満になるまで繰り返します。

LDA-VWN汎関数によってヘリウム原子のエネルギーを求めるプログラム

上述の方法によって，ヘリウム原子の（基底状態の）エネルギーを求める，C++17のプログラムは以下のようになります（多次元配列のためにBoost C++ Librariesを，また一般化固有値問題の解を求めるためにEigenを，また交換相関エネルギーおよび交換相関ポテンシャルの計算のためにLibxcを，そして数値積分のためにALGLIBをそれぞれ使っていますので，注意してください）。ただし，全部載せると非常に長くなってしまうので，一部だけを掲載しています。なお，完全なコードはGitHubのこちらで公開しています。

std::optional<double> Helium_LDA::do_scfloop()
{
    // GTOの肩の係数が格納された配列を生成
    make_alpha();

    // 1電子積分が格納された2次元配列を生成
    make_oneelectroninteg();

    // 2電子積分が格納された4次元配列を生成
    make_twoelectroninteg();

    // 重なり行列を生成
    make_overlapmatrix();

    // 全て1.0で初期化された固有ベクトルを生成
    make_c(1.0);

    // 固有ベクトルを正規化
    normalize();

    // 新しく計算されたエネルギー
    auto enew = 0.0;

    // SCFループ
    for (auto iter = 1; iter < Helium_LDA::MAXITER; iter++) {
        // Fock行列を生成
        make_fockmatrix();

        // 一般化固有値問題を解く
        Eigen::GeneralizedSelfAdjointEigenSolver<Eigen::MatrixXd> es(f_, s_);

        // E'を取得
        auto const ep = es.eigenvalues()[0];

        // 固有ベクトルを取得
        c_ = es.eigenvectors().col(0);

        // 前回のSCF計算のエネルギーを保管
        auto const eold = enew;

        // 今回のSCF計算のエネルギーを計算する
        enew = calc_energy(ep);

        std::cout << boost::format("Iteration # %2d: KS eigenvalue = %.14f, energy = %.14f\n") % iter % ep % enew;

        // SCF計算が収束したかどうか
        if (std::fabs(enew - eold) < Helium_LDA::SCFTHRESHOLD) {
            // 収束したのでそのエネルギーを返す
            return std::make_optional(enew);
        }
    }

    // SCF計算が収束しなかった
    return std::nullopt;
}

double Helium_LDA::calc_energy(double ep)
{
    // E = 2.0 * E'
    auto e = 2.0 * ep;

    for (auto p = 0; p < nalpha_; p++) {
        for (auto q = 0; q < nalpha_; q++) {
            for (auto r = 0; r < nalpha_; r++) {
                for (auto s = 0; s < nalpha_; s++) {
                    // E -= 2.0 * ΣCp * Cq * Cr * Cs * Qprqs
                    e -= 2.0 * c_[p] * c_[q] * c_[r] * c_[s] * q_[p][q][r][s];
                }
            }
        }
    }

    // E += K'
    e += calc_exc_energy();

    for (auto p = 0; p < nalpha_; p++) {
        for (auto q = 0; q < nalpha_; q++) {
            // E -= 2.0 * ΣCp * Cq * Kpq
            e -= 2.0 * c_[p] * c_[q] * k_[p][q];
        }
    }
    
    return e;
}

double Helium_LDA::calc_exc_energy() const
{
    using namespace boost::math::constants;
    
    auto const func = [this](double x)
    {
        auto rhotemp = 0.0;
        for (auto r = 0; r < nalpha_; r++)
        {
            rhotemp += c_[r] * std::exp(-alpha_[r] * x * x);
        }
        
        rhotemp *= rhotemp;

        // 電子密度
        std::array<double, 2> rho = { rhotemp, rhotemp };

        // 交換相関エネルギー
        std::array<double, 2> zk_x{}, zk_c{};

        // 交換エネルギーを求める
        xc_lda_exc(pxfunc_.get(), 1, rho.data(), zk_x.data());

        // 相関エネルギーを求める
        xc_lda_exc(pcfunc_.get(), 1, rho.data(), zk_c.data());

        return x * x * (zk_x[0] + zk_c[0]) * rhotemp;
    };

    // K'を求める
    return 8.0 * pi<double>() * gl_.qgauss(func, 0.0, Helium_LDA::MAXR);
}

void Helium_LDA::input_nalpha()
{
    while (true) {
        std::cout << "使用するGTOの個数を入力してください (3, 4 or 6): ";
        std::cin >> nalpha_;

        if (!std::cin.fail() && (nalpha_ == 3 || nalpha_ == 4 || nalpha_ == 6)) {
            break;
        }

        std::cin.clear();
        std::cin.ignore(Helium_LDA::MAXBUFSIZE, '\n');
    }
}

void Helium_LDA::make_alpha()
{
    switch (nalpha_) {
    case 3:
        alpha_ = { 0.31364978999999998, 1.1589229999999999, 6.3624213899999997 };
        break;

    case 4:
        alpha_ = { 0.297104, 1.236745, 5.749982, 38.2166777 };
        break;

    case 6:
        alpha_ =  { 0.18595935599999999, 0.45151632200000003, 1.1627151630000001, 3.384639924, 12.09819836, 65.984568240000002 };
        break;

    default:
        BOOST_ASSERT(!"make_alpha()関数のswitch文のdefaultに来てしまった！");
        break;
    }
}

void Helium_LDA::make_c(double val)
{
    c_.resize(nalpha_);
    // 固有ベクトルCの要素を全てvalで初期化
    for (auto i = 0; i < nalpha_; i++) {
        c_[i] = val;
    }
}

void Helium_LDA::make_exchcorrinteg()
{
    using namespace boost::math::constants;
    
    for (auto p = 0; p < nalpha_; p++) {
        for (auto q = 0; q < nalpha_; q++) {
            auto const func = [this, p, q](double x)
            {
                auto rhotemp = 0.0;
                for (auto r = 0; r < nalpha_; r++)
                {
                    rhotemp += c_[r] * std::exp(-alpha_[r] * x * x);
                }

                rhotemp *= rhotemp;

                // 電子密度
                std::array<double, 2> rho = { rhotemp, rhotemp };

                // 交換相関ポテンシャル
                std::array<double, 2> zk_x{}, zk_c{};

                // 交換ポテンシャルを求める
                xc_lda_vxc(pxfunc_.get(), 1, rho.data(), zk_x.data());

                // 相関ポテンシャルを求める
                xc_lda_vxc(pcfunc_.get(), 1, rho.data(), zk_c.data());

                return x * x * std::exp(-alpha_[p] * x * x) * (zk_x[0] + zk_c[0]) * std::exp(-alpha_[q] * x * x);
            };
    
            // Kpqの要素を埋める
            k_[p][q] = 4.0 * pi<double>() * gl_.qgauss(func, 0.0, Helium_LDA::MAXR);
        }
    }
}

void Helium_LDA::make_fockmatrix()
{
    // 交換相関積分を計算
    make_exchcorrinteg();

    for (auto p = 0; p < nalpha_; p++) {
        for (auto qi = 0; qi < nalpha_; qi++) {
            // Fpq = hpq + ΣCr * Cs * Qprqs + Kpq
            f_(p, qi) = h_[p][qi] + k_[p][qi];

            for (auto r = 0; r < nalpha_; r++) {
                for (auto s = 0; s < nalpha_; s++) {
                    f_(p, qi) += 2.0 * c_[r] * c_[s] * q_[p][r][qi][s];
                }
            }
        }
    }
}

void Helium_LDA::make_oneelectroninteg()
{
    using namespace boost::math::constants;

    for (auto p = 0; p < nalpha_; p++) {
        for (auto q = 0; q < nalpha_; q++) {
            // αp + αq
            auto const appaq = alpha_[p] + alpha_[q];

            // hpq = 3αpαqπ^1.5 / (αp + αq)^2.5 - 4π / (αp + αq)
            h_[p][q] = 3.0 * alpha_[p] * alpha_[q] * std::pow((pi<double>() / appaq), 1.5) / appaq -
                4.0 * pi<double>() / appaq;
        }
    }
}

void Helium_LDA::make_overlapmatrix()
{
    using namespace boost::math::constants;

    for (auto p = 0; p < nalpha_; p++) {
        for (auto q = 0; q < nalpha_; q++) {
            // Spq = (π / (αp + αq))^1.5
            s_(p, q) = std::pow((pi<double>() / (alpha_[p] + alpha_[q])), 1.5);
        }
    }
}

void Helium_LDA::make_twoelectroninteg()
{
    using namespace boost::math::constants;

    for (auto p = 0; p < nalpha_; p++) {
        for (auto qi = 0; qi < nalpha_; qi++) {
            for (auto r = 0; r < nalpha_; r++) {
                for (auto s = 0; s < nalpha_; s++) {
                    // Qprqs = 2π^2.5 / [(αp + αq)(αr + αs)√(αp + αq + αr + αs)]
                    q_[p][r][qi][s] = 2.0 * std::pow(pi<double>(), 2.5) /
                        ((alpha_[p] + alpha_[qi]) * (alpha_[r] + alpha_[s]) *
                            std::sqrt(alpha_[p] + alpha_[qi] + alpha_[r] + alpha_[s]));
                }
            }
        }
    }
}

void Helium_LDA::normalize()
{
    using namespace boost::math::constants;

    auto sum = 0.0;
    for (auto p = 0; p < nalpha_; p++) {
        for (auto q = 0; q < nalpha_; q++) {
            sum += c_[p] * c_[q] / (4.0 * (alpha_[p] + alpha_[q])) * std::sqrt(pi<double>() / (alpha_[p] + alpha_[q]));
        }
    }

    for (auto p = 0; p < nalpha_; p++) {
        c_[p] /= std::sqrt(4.0 * pi<double>() * sum);
    }
}

なお，このプログラムは，参考サイト[1]のhelium_hf_gauss.cを参考にさせて頂きました。また，$ n = 3 $および$ n = 6 $の場合の$ \alpha_{p} $の値は，参考サイト[2]の，basis-sto3g.cppおよびbasis-sto6g.cppから引用させて頂きました。

プログラムの実行結果

前節で紹介したプログラムを実行した結果は，以下の画像のようになります。

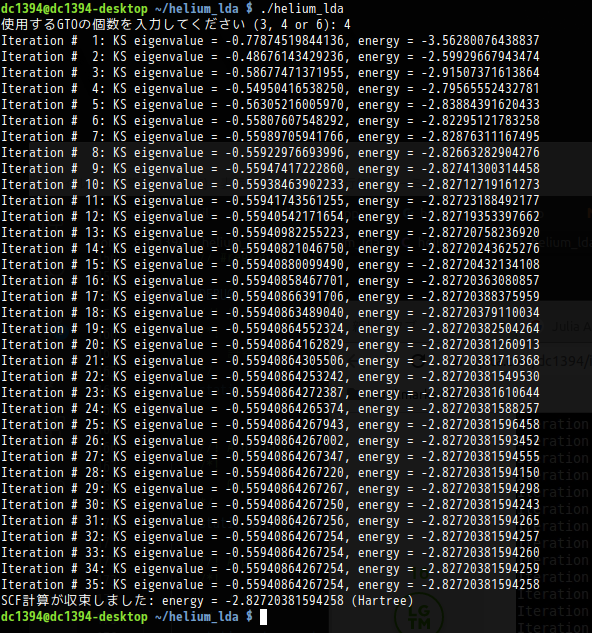
$ n = 4 $で，固有ベクトル$ \vec{C} $の要素$ C_{p} $の初期値がすべて1の場合，$ \left\vert E_{new}-E_{old}\right\vert $が，閾値（今の場合$ 10^{-14} $）未満になるまでに，35回のループを要していることが分かります。

プログラムによるヘリウム原子のエネルギーの計算結果の結果と考察

ここで，このプログラムによる$ n = 3 $，$ n = 4 $，$ n = 6 $のときのエネルギーの計算結果を表に示しますと，以下のようになります（単位は全てHartree原子単位です）。比較のために，Hartree-Fock法による$ n = 3 $，$ n = 4 $，$ n = 6 $のときの計算結果も，併せて示しました。

n	Kohn-Sham (LDA-VWN)	Hartree-Fock
3	-2.7872	-2.8162
4	-2.8272	-2.8552
6	-2.8330	-2.8600
無限個の基底を用いた極限	−2.8348	−2.8617
厳密	−2.9037	−2.9037

上記の表を見ると，LDA-VWN汎関数を用いたKohn-Sham法による計算結果は，$ n = 3 $，$ n = 4 $，$ n = 6 $，また無限個の基底による極限（この値は，有限要素法によって高精度にKohn-Sham方程式を解く拙作のコードの計算結果と，GAMESS (US)による計算結果を照合して求めました）の場合のいずれも，Hartree-Fock法による計算結果に劣っていることが分かります。これは一体なぜなのでしょうか（ただし，Hartree-Fock法と比べて劣っていると言っても，厳密な計算結果と比較して，2.4%の過小評価（無限個の基底を用いた極限の場合）であり，厳密な計算結果と比較して，33%も過大評価するThomas-Fermiモデルより，遙かに良くなっていることには注意すべきです）。結論から言うと，この原因は，上述した自己相互作用にあります。自己相互作用については，既に簡単に説明しましたが，これはKohn-Sham法における大問題であり，また別の記事で詳しく説明していきたいと思います。

#参考文献
[1] P. A. M. Dirac, (Mathematical) Proceedings of the Cambridge Philosophical Society 26, 376 (1930).
[2] J. C. Slater, Phys. Rev. 81(3), 385 (1951).
     doi:10.1103/PhysRev.81.385
[3] S. H. Vosko, L. Wilk, and M. Nusair, Can. J. Phys. 58, 1200 (1980).
     doi:10.1139/p80-159

#参考サイト
[1] Numerical Methods in Quantum Mechanics
[2] HFCXX - Hartree-Fock C++ code