Julia 0.6.2でTensorFlow。
今回は線形基底関数を用いた回帰。TensorFlowへの入れ方を少し工夫してみる。
TensorFlowにデータを入れるときにやりやすいように、行列とベクトルを使った形に整理した。
また、前回の記事で扱った過学習についても、もう一度やってみた。
これまでの記事はこちら。
JuliaでTensorFlow その1
https://qiita.com/cometscome_phys/items/358bc4a1feaec1c7fa14
JuliaでTensorFlow その2: 線形回帰をやってみる
https://qiita.com/cometscome_phys/items/244cfed8ab309156735c
JuliaでTensorFlow その3: 過学習について
https://qiita.com/cometscome_phys/items/638dca2c980ab0f98a9e
線形基底関数
前回の記事
https://qiita.com/cometscome_phys/items/638dca2c980ab0f98a9e
で、多項式を使ったフィッティング:
$$
y = \sum_{i=1}^n a_i x^i + b
$$
を使った。今回は、これを少し拡張してみる。
まず、上の式の$b$というのは少し収まりが悪い気がするので、上の式を
$$
y = \sum_{i=0}^n a_i x^i
$$
としてみよう。$x^0 = 1$なので、$a_0 = b$となっている。
さて、フィッティングをしたければ、別に$x^i$を使う必要がないことに気づくだろうか?
つまり、適当な関数$\phi_i(x)$を用いて
$$
y = \sum_{i=0}^n a_i \phi_i(x)
$$
としてフィッティングをしても、問題はない。例えば、$\phi_i(x) = \cos (k_i x)$とすれば、偶関数のフーリエ変換となる。ここで、$\phi_0(x)=1$と約束しておけば、定数$b$の効果が自動的に入る。
なお、変数が$x$以外に複数あったとして、$\phi_i(x,y)$などとおいてフィッティングを考えれば、全く同じようにできることがわかる。
行列とベクトルを使った表記
さて、TensorFlowを使って計算を行う際に便利な書き方について考えておこう。
TensorFlowは文字通りテンソルを使った演算なので、テンソル、行列、ベクトル、を使った表記の親和性が高いと考えられる。
これまでの記事では、ずっとインプットを$x$としてきた。
もし、このまま続ける場合、$\phi_i(x)$を求める計算をTensorFlowの中で計算することになる。それだとどんどん複雑なものを考えると、大変になると予想される。そこで、インプットを$\phi_i(x)$としてみよう。つまり、
\vec{\phi}(x) =
\left(
\begin{matrix}
1 \\
\phi_1(x) \\
\phi_2(x) \\
\vdots \\
\phi_{n-1}(x)
\end{matrix}
\right)
という$n$次元ベクトルをインプットとしてみよう。この時、フィッティングは
$$
y = \vec{a}^T \vec{\phi}(x)
$$
と書ける。ここで、$\vec{a}$も$n$次元ベクトルである。
次に、データ点が複数ある場合を考えよう。データ点の数が$m$個のとき、
\vec{y} =
\left(
\begin{matrix}
y_1 \\
y_2(x) \\
\vdots \\
y_{m}(x)
\end{matrix}
\right)
というベクトルを用意すると、全体は
\vec{y}^T = \vec{a}^T \left(
\begin{matrix}
\vec{\phi}(x_1) & \vec{\phi}(x_2) &\cdots & \vec{\phi}(x_m)
\end{matrix}
\right)
という形で書ける。右辺の$\vec{\phi}$からなる行列を$\hat{\phi}$とすると、
$$
\vec{y}^T = \vec{a}^T \hat{\phi}
$$
という綺麗な形で書ける。
グラフの設計
Juliaでグラフを描いてみよう。functionを使ってグラフ設計を書くと、
function build_graph(d_input)
x = placeholder(Float64)
yout = placeholder(Float64)
a = Variable(ones(Float64,1,d_input))
y = a*x
diff = y-yout
loss = nn.l2_loss(diff)
optimizer = train.AdamOptimizer()
minimize = train.minimize(optimizer, loss)
return x,a,y,yout,diff,loss,minimize
end
となる。加えて、行列$\hat{\phi}$を作るfunctionは
function make_φ(x0,n,k)
φ = zeros(Float64,k,n)
for i in 1:k
φ[i,:] = x0.^(i-1)
end
return φ
end
となる。ここでは、基底関数として$ x^i$を用いている。このfunctionをいじることで、簡単に基底関数を変更することができる。
元データの生成
元のデータを、
$$
y = a_1 x + a_2 x^2 + b + 3 cos(20 x)
$$
としてみる。今回は、ランダムノイズの代わりに、高速で振動する関数を足しておいた。
データセットは、
using Plots
ENV["PLOTS_TEST"] = "true"
gr()
n = 10
x0 = linspace(-2,2,n)
a0 = 3.0
a1= 2.0
b0 = 1.0
y0 = zeros(Float64,1,n)
f(x0) = a0.*x0 + a1.*x0.^2 + b0 + 3*cos.(20*x0)
y0[1,:] = f(x0)
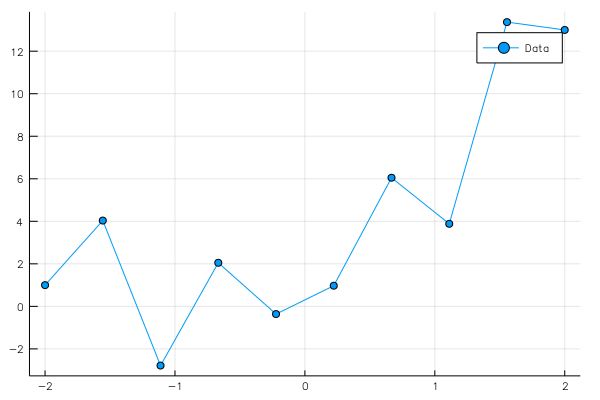
pl=plot(x0,y0[1,:],marker=:circle,label="Data")
savefig("data2.png")
pl
グラフの実行
グラフの実行は
φ = make_φ(x0,n,4)
x,a,y,yout,diff,loss,minimize = build_graph(4)
sess = Session()
run(sess, global_variables_initializer())
nt = 10000
for i in 1:nt
run(sess, minimize, Dict(x=>φ,yout=>y0))
if i%1000==0
losstrain = run(sess, loss, Dict(x=>φ,yout=>y0))
#losstest = run(sess, loss, Dict(x=>x0test,yout=>y0test))
# test: ", losstest)
println(i,"\t",losstrain)
end
end
ye = run(sess, y, Dict(x=>φ,yout=>y0))
close(sess)
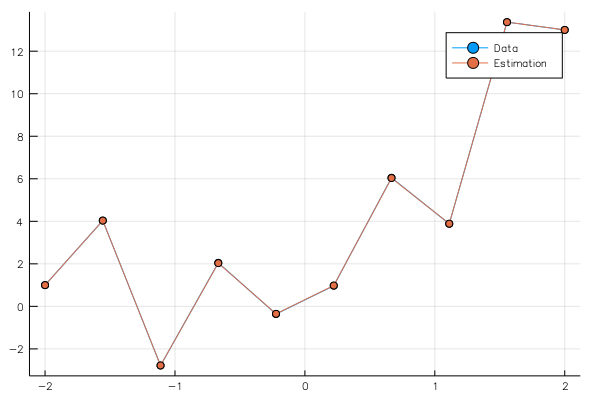
pls = plot(x0,[y0[1,:],ye[1,:]],marker=:circle,label=["Data","Estimation"])
savefig("comparison_2.png")
と書ける。ここで、Juliaにおいて、1xnのベクトルとn次元横ベクトルを区別する必要が生じたため、少し回りくどいことをしている。これを回避できる方法があるかどうかはわからない。
グラフは
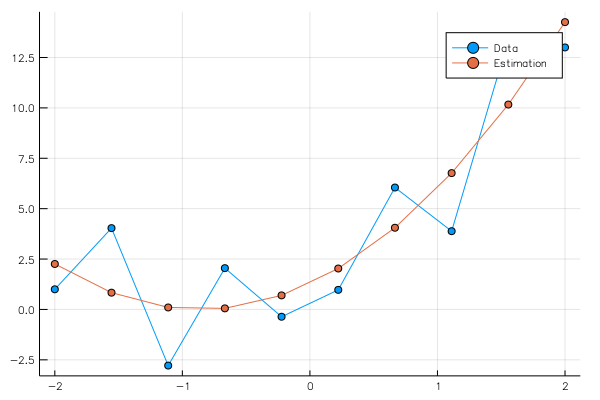
となる。ここでは、3次関数を使ってフィッティングしている。
過学習について
前回の記事ではあまり過学習としてふさわしいものではなかったという指摘があったので、別のケースの過学習について考える。今回はノイズではなくcos関数を使っている。
コードを少し一般化したため、もう少し高次の多項式を使ってみよう。
k = 13
φ = make_φ(x0,n,k)
x,a,y,yout,diff,loss,minimize = build_graph(k)
sess = Session()
run(sess, global_variables_initializer())
nt = 10000*50
for i in 1:nt
run(sess, minimize, Dict(x=>φ,yout=>y0))
if i%10000==0
losstrain = run(sess, loss, Dict(x=>φ,yout=>y0))
println(i,"\t",losstrain)
end
end
ye = run(sess, y, Dict(x=>φ,yout=>y0))
pls = plot(x0,[y0[1,:],ye[1,:]],marker=:circle,label=["Data","Estimation"])
savefig("comparison_2.png")
close(sess)
φを作るにあたって、13という数字を入れているので12次の多項式までを使っていることになる。
このlossが収束するには大分時間がかかったため、500000回回してみた。
その結果、
とほぼ完全にフィッティングすることができた。
オリジナルの関数はわかっているので、このフィッティングで得られた係数を使って、$-2 \le x \le 2$の区間の別の点がフィッティングできるか試してみよう。
n = 100
x02 = linspace(-2,2,n)
a0 = 3.0
a1= 2.0
b0 = 1.0
y02 = zeros(Float64,1,n)
f(x0) = a0.*x0 + a1.*x0.^2 + b0 + 3*cos.(20*x0)
y02[1,:] = f(x02)
pl=plot(x02,y02[1,:],marker=:circle,label="Data")
savefig("data2_test.png")
φ2 = make_φ(x02,n,k)
ye2 = ae*φ2
pls = plot(x02,[y02[1,:],ye2[1,:]],marker=:circle,label=["Data","Estimation"])
savefig("comparison_2_test.png")
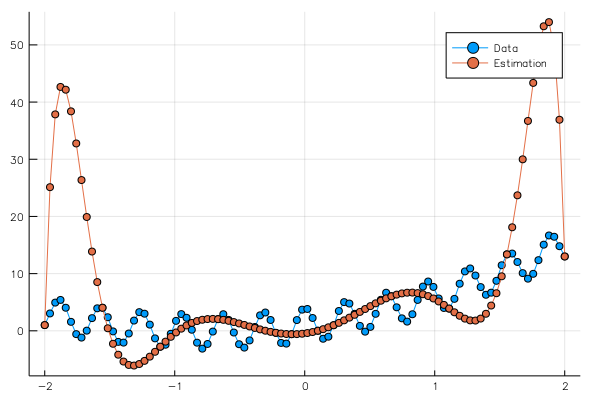
このコードを実行して得られたグラフは
となり、lossを非常に小さくしたにもかかわらず、全体の関数は全然合っていない。
これは、前回の記事でも述べたが、トレーニングデータを大量のパラメータで完全にフィッティングさせたことにより、テストデータのフィッティングが全然ダメになってしまっている。これが、過学習である。