Julia 0.6.2でTensorFlowを使う。その2。
その1は
https://qiita.com/cometscome_phys/items/358bc4a1feaec1c7fa14
ここでは、簡単な線形回帰をやってみる。
元のデータの生成
まずはじめに、元のデータを
$$
y = ax+b +{\rm noise}
$$
として作る。ここで、noiseを適当に発生させておくことで、データが直線からずれることになる。
このようなズレがある場合に、元の直線を推測できるか($a$と$b$を推測できるか)、という問題。
元の直線は
using Plots
ENV["PLOTS_TEST"] = "true"
gr()
n = 10
x0 = linspace(-1,1,n)
noise = 0.5*rand(linspace(-1,1),n)
a0 = 3.0
b0 = 1.0
y0 = a0.*x0 + b0 + noise
plot(x0,y0,marker=:circle,label="Data")
savefig("data.png")
で描くことができる。
これを実行すると
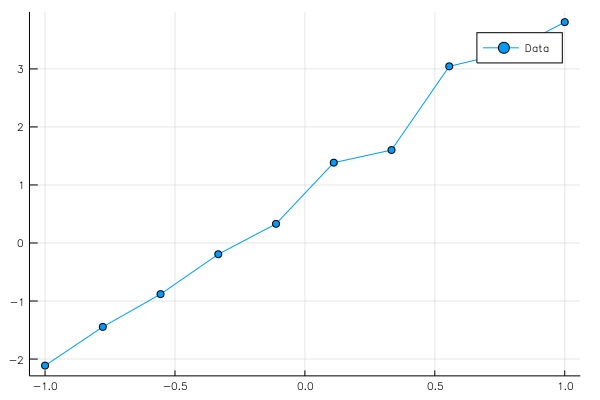
というグラフが得られる。
なお、Plotsのバックエンドのgrが6倍大きな図を作ってしまう問題があるので、ENV["PLOTS_TEST"] = "true" を使っている。詳しくは
http://nbviewer.jupyter.org/gist/genkuroki/3d6dbf52a3e52eb7c664bc88632c81d3
を参照。
グラフの設計
次に、その1と同じようにグラフを設計してみよう。
まず、$x_i$をインプットデータ、$y_i$をアウトプットデータとして、この$(x_i,y_i)$の組が複数ある状況を考える(上のコードでは10個)。
そして、
データが
$$
y_i = a x_i + b
$$
という直線に従っていると仮定する。
この仮定のもと、一番もっともらしい$a$と$b$を求めるのが線形回帰である。
そして、二乗誤差:
$$
{\rm loss} = \sum_i (y - y_i)^2
$$
が一番小さくなるような$a$と$b$が、一番もっともらしいとする。
TensorFlowでは、何かの関数を最小化することが簡単にできる。
何を最小化するか、どのように最小化するかの情報を設定しておけばよい。
その1の小人の例で例えると、小人Bに「最小化しろ」といえばあとはよしなにやってくれるのである。
まず、小人Aへの指令(グラフ作成)は
using TensorFlow
x = placeholder(Float64)
yout = placeholder(Float64)
a = Variable(2.0)
b = Variable(0.0)
y = a.*x+b
diff = y-yout
loss = nn.l2_loss(diff)
optimizer = train.AdamOptimizer()
minimize = train.minimize(optimizer, loss)
となる。ここでは、minimizeを小人Bに指定すれば、lossを最小化してくれることになる。
グラフの実行
次に、実際の計算を小人Bにやらせるコードは
sess = Session()
run(sess, global_variables_initializer())
nt = 10000
for i in 1:nt
run(sess, minimize, Dict(x=>x0,yout=>y0))
if i%1000==0
println(i,"\t",run(sess, loss, Dict(x=>x0,yout=>y0)))
end
end
となる。
出力結果は
1000 0.5525778742090897
2000 0.2062854331360348
3000 0.20391311222929595
4000 0.20391251120152726
5000 0.20391251120114107
6000 0.203912511201141
7000 0.2039125112011411
8000 0.20391251120114104
9000 0.20391251120114096
10000 0.20391251120114093
となる。
ここで、最小化は逐次的に行われるので、何回も繰り返すことで少しずつlossが小さくなっていくことに注意。ある程度まで回数をこなすと、lossの値は変わらなくなる。この時、今仮定している線形のモデルでの最良の$a$と$b$が得られている可能性が高い(今後言及する「過学習」が起きた場合には、その限りではない)。
最後に、$a$や$b$の値を表示させ、グラフをプロットするには、
ae = run(sess, a)
be = run(sess, b)
ye = run(sess, y, Dict(x=>x0,yout=>y0))
println("a = ", ae," b = ", be)
close(sess)
plot(x0,[y0,ye],label=["Data","Estimation"],marker=:circle)
とすればよい。そして、
a = 3.0662337662337653 b = 0.8816326530612243
という値が得られる。
グラフは
となる。
それなりにいい感じにフィッティングされている。
