LoginSignup
8
7

More than 5 years have passed since last update.

@cometscome_phys(Yuki Nagai)

JuliaでTensorFlow その5: ニューラルネットワークの導入と深層学習

Last updated at Posted at 2018-04-12

Julia 0.6.2でTensorFlow。
今回は前回の流れのままニューラルネットワークを導入する。

これまでの記事はこちら。
JuliaでTensorFlow その1
https://qiita.com/cometscome_phys/items/358bc4a1feaec1c7fa14
JuliaでTensorFlow その2: 線形回帰をやってみる
https://qiita.com/cometscome_phys/items/244cfed8ab309156735c
JuliaでTensorFlow その3: 過学習について
https://qiita.com/cometscome_phys/items/638dca2c980ab0f98a9e
JuliaでTensorFlow その4: 線形基底関数を用いた回帰
https://qiita.com/cometscome_phys/items/92dba9f82cd58d877ec5

これまでのおさらい

ある$(x,y)$のデータセットがあるとする。
これまで、インプットを$x$、アウトプットを$y$として、
$$
y = f(x)
$$
という関係があるとして、この$f$を求めることを行ってきた。線形回帰の場合には、
$$
y = a x + b
$$
となり、線形基底関数を用いた場合には
$$
y = \sum_{i=0}^n a_i \phi_i(x)
$$
となる。ここで、$\phi_i(x)$は何らかの$x$の関数である。$\phi_0(x) = 1$としておく。
データ点の数が$m$個のとき、

\vec{y} = 
\left(
\begin{matrix}
y_1 \\
y_2(x) \\
\vdots \\
y_{m}(x)
\end{matrix}
\right)

を用意すれば、

\vec{y}^T = \vec{a}^T \left(
\begin{matrix}
\vec{\phi}(x_1) & \vec{\phi}(x_2) &\cdots & \vec{\phi}(x_m)
\end{matrix}
 \right) \\
=\vec{a}^T  \hat{\phi}

とコンパクトな形で書くことができる。

これは、入力として行列$\hat{\phi}$を与えた時に、出力として$\vec{y}$が出てくるようなパラメータ$\vec{a}$を求める問題であり、線形な問題である。なぜなら、$\hat{\phi}$を二つ用意して、それぞれで$\vec{y}$を求めて和をとったものと、二つの和を入力として、出力を求めたものが、同じになるからである。

様々なデータは基本的にはこの形で書くことができる。なぜなら、オリジナルが従う関数$f$がわかっていれば、$\phi_1(x) = f(x)$とおけば、どんな関数もフィッティングできるからである。
しかし、$\phi_i(x)$にどんな関数を選ぶかが、問題である。多くの場合、関数$f$がわからないからフィッティングをするのであって、良い基底関数は$\phi_i(x)$は手作業で探すことになる。

なお、入力が$x$ではなく$\vec{x}^T = (x_1,x_2,\cdots)$のように多次元になった場合には、$\phi_i(\vec{x})$という基底関数を選んでくれば、同様にフィッティングができる。もちろん、良い関数を見つけるのはさらに困難になる。
どちらにせよ、インプットが複数、アウトプットが一つという形であれば、いつもこのような形で線形回帰を実行することができる。

非線形関数へ

良い基底関数を探す、ということばかりでは一向にフィッティングが向上しない場合も、実用上多い。よって、より表現力の高い関数を用いてフィッティングを行えば、使っている基底関数が同じだとしてもよりよりフィッティングが得られる可能性がある。
表現力を高めるためには、パラメータを増やせば良い。どうすればよいだろうか。
さて、$n$次元ベクトル$\vec{a}$を、$k$次元ベクトル$\vec{b}$と$k \times n$行列$\hat{W}$を用いて

\vec{a}^T =  \vec{b} \hat{W}

と分解してみよう。これを用いると、

\vec{y}^T = \vec{b} \hat{W} \hat{\phi}

となり、見かけ上パラメータが増えている。
しかし、本当のパラメータは$n$しかない。なぜなら、要素で書くと

y_i = \sum_j^n \sum_k^m [\vec{b}]_k W_{kj} \phi_{ji}

となり、$k$の和は$\phi_{ij}$に影響を与えずに

\sum_k^m [\vec{b} ]_k W_{kj} = a_j

とくくれてしまうからである。
これをくくれなくすれば、パラメータを増やすことができる。つまり、

y_i = \sum_j^n \sum_k^m [\vec{b}]_k g(W_{kj} \phi_{ji})

と途中に非線形な関数$g$を挟めばよい。これにより、$\vec{y}$は$\vec{a}$では表現できなくなり、
パラメータが増えることになる。

ニューラルネットワークと深層学習

さらに、

x_{ki} = \sum_j^n g(W_{kj} \phi_{ji})

という行列$\hat{x}$を導入すれば、

\vec{y}^T = \vec{b} \hat{x} \\
\hat{x} = g(\hat{W}\hat{\phi})

という形に二つに分けることができる。
さらに、$\vec{b}$を分解すれば、同様のことを何度でも繰り返し行うことができ、パラメータが増えていく。
例えば、

\hat{x}_1 = g(\hat{W}_1 \hat{\phi}) \\
\hat{x}_2 = g(\hat{W}_2 \hat{x}_1) \\
\vdots \\
\hat{x}_N = g(\hat{W}_N \hat{x}_{N-1}) \\
\vec{y}^T = \vec{a} \hat{x}_N

とすれば、パラメータは$\vec{a}$及び$\hat{W}_1,\cdots,\hat{W}_N$となり、大量のパラメータを作ることができる。これが、ニューラルネットワークである。このようにたくさん関数を重ねると、これは、ディープニューラルネットワークとなり、これはつまり深層学習である。
このように非常にたくさんあるパラメータをどうやって最適化するのか？そのあたりは様々な機械学習の本やwebにあるので、ここでは割愛する（TensorFlowの小人Bが良い仕事をしてくれる）。ともかく、これが可能になったことにより、機械学習は大きく花開くこととなった。
どのあたりがニューロンなのか、というと、$g$が活性化関数と言われ、ある値を境に値が増えるような関数(ニューロンの発火)が用いられるからである。
詳しくは
"活性化関数のまとめ（ステップ、シグモイド、ReLU、ソフトマックス、恒等関数）"
https://qiita.com/namitop/items/d3d5091c7d0ab669195f
こちらの記事などを参照。

Juliaでの実装

グラフの設計

以前の記事のグラフは

test.jl
function build_graph(d_input)
    x = placeholder(Float64)
    yout = placeholder(Float64)
    a = Variable(ones(Float64,1,d_input))
    y = a*x    
    diff = y-yout
    loss = nn.l2_loss(diff)
    optimizer = train.AdamOptimizer()
    minimize = train.minimize(optimizer, loss)
    return x,a,y,yout,diff,loss,minimize
end

である。これを少し変更すれば良い。つまり、

test2.jl
function build_graph(d_input,d_middle,d_type)
    x = placeholder(d_type)
    yout = placeholder(d_type)    
    a = Variable(ones(d_type,1,d_middle))

    W = Variable(rand(d_type,d_middle,d_input))
    x1 = nn.relu(W*x)    
    y = a*x1

    diff = y-yout
    loss = nn.l2_loss(diff)
    optimizer = train.AdamOptimizer()
    minimize = train.minimize(optimizer, loss)
    return x,a,y,W,yout,diff,loss,minimize
end

と書き換えれば、隠れ層一層のニューラルネットワークとなる。

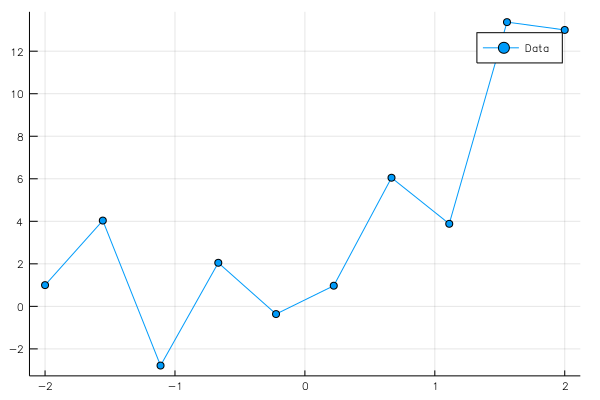
オリジナルのデータは、前回の記事と同じように、

test2.jl
using Plots
ENV["PLOTS_TEST"] = "true"
gr()
n = 10
x0 = linspace(-2,2,n)
a0 = 3.0
a1= 2.0
b0 = 1.0
y0 = zeros(Float64,1,n)
f(x0) = a0.*x0 + a1.*x0.^2 + b0 + 3*cos.(20*x0)
y0[1,:] = f(x0)
pl=plot(x0,y0[1,:],marker=:circle,label="Data")
savefig("data2.png")
pl

data2.png
としておく。

グラフの計算

実際に実行してみよう。前半部分は上の書いたグラフの設計部分である。入力の関数は多項式として、3次まで用いた。隠れ層のユニットの数は10とした。

test2.jl
using TensorFlow
srand(12)

function build_graph(d_input,d_middle,d_type)
    x = placeholder(d_type)
    yout = placeholder(d_type)    
    a = Variable(ones(d_type,1,d_middle))

    W = Variable(rand(d_type,d_middle,d_input))
    x1 = nn.relu(W*x)    
    y = a*x1

    diff = y-yout
    loss = nn.l2_loss(diff)
    optimizer = train.AdamOptimizer()
    minimize = train.minimize(optimizer, loss)
    return x,a,y,W,yout,diff,loss,minimize
end

k=4
function make_φ(x0,n,k)
    φ = zeros(Float64,k,n)
    for i in 1:k
        φ[i,:] = x0.^(i-1)
    end
    return φ
end

φ = make_φ(x0,n,k)
d_type = Float32
d_input = k
d_middle = 10
x,a,y,W,yout,diff,loss,minimize = build_graph(d_input,d_middle,d_type)


sess = Session()
run(sess, global_variables_initializer())

nt = 50000
for i in 1:nt
    run(sess, minimize, Dict(x=>φ,yout=>y0))
    if i%1000==0
        losstrain = run(sess, loss, Dict(x=>φ,yout=>y0))
        println(i,"\t",losstrain)
    end
end

ye = run(sess, y, Dict(x=>φ,yout=>y0))

pls = plot(x0,[y0[1,:],ye[1,:]],marker=:circle,label=["Data","Estimation"])
savefig("data_n.png")
pls

結果は
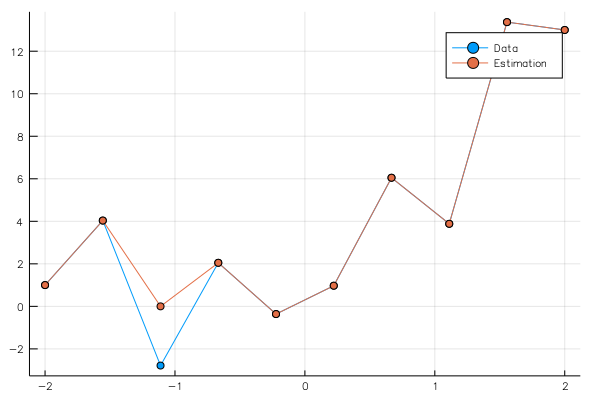
data_n.png
となる。
これだけでは、過学習している可能性が極めて高い。
実際、

test2.jl
n = 100
x02 = linspace(-2,2,n)
φ2 = make_φ(x02,n,k)
y02 = zeros(Float64,1,n)
y02[1,:] = f(x02)
yt = run(sess, y, Dict(x=>φ2))
pls = plot(x02,[y02[1,:],yt[1,:]],marker=:circle,label=["Data","Estimation"])
savefig("data_nd.png")
close(sess)
pls

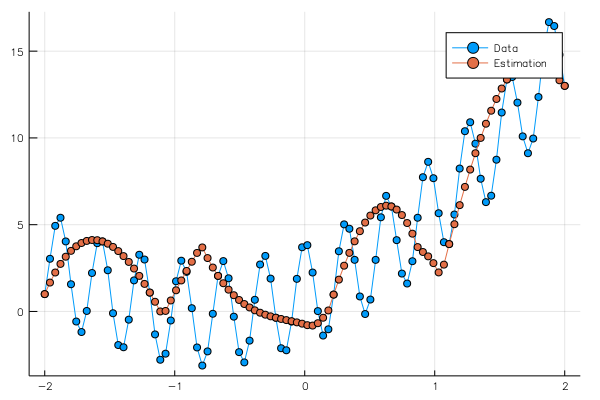
で見てみると、

data_n.png
となっており、与えたデータ点以外では合っていない。

過学習の克服

過学習を克服するためには、様々なデータをインプットとして与える方法がある。
データ点$(x,y)$が100点あるとする。このデータ点から10個ランダムに選んできて、それを用いて学習を行う。それを10回繰り返してみよう。コードは、

test2.jl
n= 100
x0 = linspace(-2,2,n)
φ = make_φ(x0,n,k)
y0 = zeros(Float64,1,n)
y0[1,:] = f(x0)
d_type = Float32
d_input = k
d_middle = 10
x,a,y,W,yout,diff,loss,minimize = build_graph(d_input,d_middle,d_type)


sess = Session()
run(sess, global_variables_initializer())

nt = 1000
nk = 10
for k in 1:nk
    batchsize = 10
    A = shuffle!(collect(1:1:n))
    φ_b = zeros(d_type,d_input,batchsize)
    y0_b = zeros(d_type,1,batchsize)
    for j in 1:batchsize        
        φ_b[:,j] = φ[:,A[j]]
        y0_b[1,j] = y0[1,A[j]]
    end


    for i in 1:nt
        run(sess, minimize, Dict(x=>φ,yout=>y0))
        if i%1000==0
            losstrain = run(sess, loss, Dict(x=>φ_b,yout=>y0_b))/batchsize
            println(i,"\t",losstrain)
        end
    end
end

ye = run(sess, y, Dict(x=>φ,yout=>y0)) #Test Data


pls = plot(x0,[y0[1,:],ye[1,:]],marker=:circle,label=["Data","Estimation"])
savefig("data_nb.png")
pls

である。学習に使うデータを選ぶ際、インデックスを$A$に入れてシャッフルすることで、ランダムなデータ点を取ってくるようにしている。
結果は、
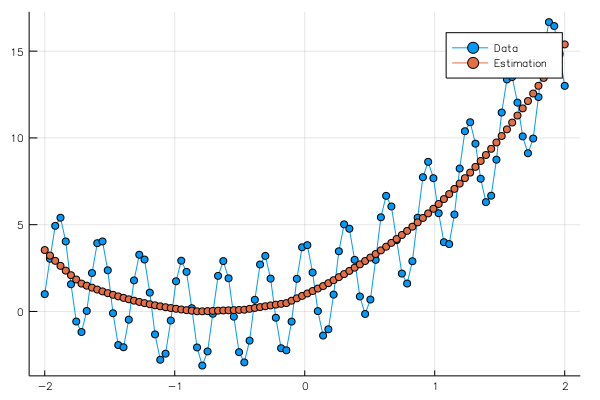
data_nb.png
となった。cosの振動の影響をあまり受けない綺麗なグラフを得ることができた。
ここで、注意することとして、バッチサイズ（学習に使うデータの数）やトレーニングの回数、バッチの数などで結果はかなり大きく変化する、ということがある。もちろん、用意する層の数やユニットの数にも依存する。これらのパラメータをハイパーパラメータと呼び、このチューニングに技術や経験が必要だったりする。

8
7
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
8
7