LoginSignup
4
10

More than 1 year has passed since last update.

@cometscome_phys(Yuki Nagai)

Juliaで機械学習：深層学習フレームワークFlux.jlを使ってみる　その3：ニューラルネットとバッチ正規化編

Last updated at Posted at 2018-09-29

この記事は
"Juliaで機械学習：深層学習フレームワークFlux.jlを使ってみる　その１：基本編"
https://qiita.com/cometscome_phys/items/e99d6177325e78ebb228
"Juliaで機械学習：深層学習フレームワークFlux.jlを使ってみる　その２：線形回帰編"
https://qiita.com/cometscome_phys/items/f58174c0dad7ecb811ed
の続きである。Batch Normalization （バッチ正規化）を実装してみよう。

今回は、
"TensorFlowの高レベルAPIを使ったBatch Normalizationの実装"
https://qiita.com/cometscome_phys/items/6d5d3c74d7000382efef
をJulia 1.0とFluxでやってみる。

バッチ正規化とは

このセクションは
"TensorFlowの高レベルAPIを使ったBatch Normalizationの実装"
https://qiita.com/cometscome_phys/items/6d5d3c74d7000382efef
から再掲したものである。

学習用のインプットデータをランダムにピックアップしたものをバッチと呼ぶが、これは、ランダムに何度もピックアップすることで、過学習を避ける仕組みである。
Batch Normalizationとは、ニューラルネットの途中で、バッチの平均を0分散を1に処理:
$$
y \leftarrow \gamma (y-\mu)/\sqrt{\sigma^2+\epsilon} + \beta
$$
する方法である。ここで、$\gamma$と$\beta$は学習される。$\epsilon$はゼロ割を避けるための小さな正の数である。また、トレーニング時には$\mu$はバッチの平均、$\sigma$はバッチの分散が入る。テスト時には$\mu$と$\sigma$は移動平均と移動分散を入れることになる。
これを用いると、収束の高速化などが期待される。
原論文は
Sergey Ioffe, Christian Szegedy,
"Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift"
https://arxiv.org/abs/1502.03167
にある。
日本語の解説などは
https://qiita.com/t-tkd3a/items/14950dbf55f7a3095600
等がわかりやすい。

バージョン

Julia 1.0.0
Flux v0.6.7

->
Julia 1.6.1
Flux 0.12.6

一部のコードが動かなくなっていたのを修正

再現すべき関数

前回の記事と同じ関数である。パラメータ等はTensorFlowの記事と同じにした。

test.jl
n = 300
x0 = range(-2,length=n,stop=2) #Julia 1.0.0以降はlinspaceではなくこの書き方になった。
a0 = 3.0
a1= 2.0
b0 = 1.0
y0 = zeros(Float32,n)
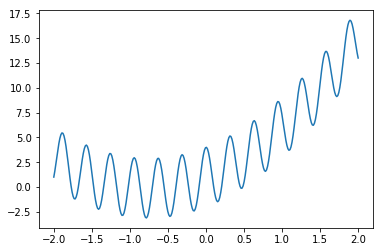
f(x0) = a0.*x0 .+ a1.*x0.^2 .+ b0 .+ 3*cos.(20*x0)
y0[:] = f.(x0)

グラフは

Unknown-4.png
となる(TensorFlowの記事からの再掲)。

インプットデータの生成

ここはこれまでの記事とほとんど同じである。

test.jl
function make_φ(x0,n,k)
    φ = zeros(Float32,k,n)
    for i in 1:k
        φ[i,:] = x0.^(i-1)
    end
    return φ
end
k = 6
φ = make_φ(x0,n,k)

前回の記事と変更点は、TensorFlowの記事に合わせるように$k=4$から$k=6$としたことである。

モデルの構築

モデルを構築する。
Flux.jlでは、

test.jl
using Flux
d_input = k
d_middle = 10
d_output = 1
model = Chain(
    Dense(d_input, d_middle,σ), #一層目。活性化関数にreluを使用
    BatchNorm(d_middle), #バッチ正規化　
    Dense(d_middle, d_output) #二層目
    )

でニューラルネットを作ることができる。BatchNormを挟むことで、バッチ正規化層を導入できる。活性化関数を最初のレイヤーにいれるかBatchNormに入れるかは好みであるが、今回はTensorFlowの記事に合わせることにした。なお、配列の一番左端がインプットの次元となっているようである。
このモデルにインプット配列φを入れるとアウトプットが返ってくるが、一つ注意点がある。
インプット配列は1次元ではだめで、少なくとも2次元はなければならない（3次元以上は確認していない）。つまり、

test.jl
Flux.testmode!(model) #Batchの平均と分散を更新しないようにする。つまりテストモード。
println("model 2 inputs: ",model(φ[:,1:2]))
Flux.testmode!(model,false) #テストモードを終了する。

は動くが、

test.jl
Flux.testmode!(model) #Batchの平均と分散を更新しないようにする。つまりテストモード。
println("model 1 input: ",model(φ[:,1]))
Flux.testmode!(model,false) #テストモードを終了する。

はエラーが出て動かない。なお、Flux.testmode!(model)を呼ぶと、BatchNorm層でバッチの平均と分散を更新しないようになる。つまり、Testの時にはこれを呼ぶ必要がある。
データ点が1点しかないときには、配列を1次元行列から2x1の2次元配列にすればよい。つまり、reshape(A,(:,1))を使えばよい（もっと良い方法があるかもしれない）：

test.jl
Flux.testmode!(model) #Batchの平均と分散を更新しないようにする。つまりテストモード。
println("model 1 inputs: ",model(reshape(φ[:,1],(:,1))))
Flux.testmode!(model,false) #テストモードを終了する。

このmodelの学習させるパラメータは、1層目のWとb、BatchNorm層のβとγ、2層目のWとbである。これらは、

test.jl
#=
println(model[1].W.data) #W
println(model[1].b.data) #b

println("β ",model[2].β.data)
println("γ ",model[2].γ.data)
println("μ ",model[2].μ)
println("σ ",model[2].σ)

println(model[3].W.data)
println(model[3].b.data)
=#

println(model[1].W) #W
println(model[1].b) #b

println("β ",model[2].β)
println("γ ",model[2].γ)
println("μ ",model[2].μ)
println("σ² ",model[2].σ²)

println(model[3].W)
println(model[3].b)

などで取り出せる。μとσは平均値と分散で、これは学習させるパラメータではないために、Trackedな変数ではない。したがって、dataをつけずに取り出さなければならない。

最適化

最小化するべきloss関数として、平均二乗誤差を考える。前回の記事ではFlux.jlのmseという関数を使っていたが、バッチでデータを入れる時には問題が生じる。mseはソースコード(Flux.jl/src/layers/stateless.jl)をみると

test.jl
mse(ŷ, y) = sum((ŷ .- y).^2)/length(y)

と定義されている。このsumの中身を

test.jl
diff(ŷ, y) = (ŷ .- y).^2
println("diff ",diff(model(φ[:,1:2]),y0[1:2]))

で見てみると、

test.jl
diff Flux.Tracker.TrackedReal{Float64}[1.89654e-8 (tracked) 3.99294 (tracked); 0.354942 (tracked) 6.72814 (tracked)]

となってしまい、2x2行列となっている。これは、y0が普通の型であり、model(φ[:,1:2])がFlux.jlのTracked型であるために、要素の差.-が予想と異なる挙動をしたためである。バッチサイズが2なので成分が二つの1次元配列あるいは2x1配列が欲しい。よって、loss関数を

test.jl
loss(x, y) =  sum([(y[i] .- model(x)[i]).^2 for i=1:length(y) ])/length(y)

とした。これは、xがインプットデータの次元とバッチの次元の2次元であると仮定したloss関数である。forループでバッチのそれぞれの要素を足し合わせている。

最適化は前回の記事と同じADAMを使用する。

test.jl
#opt = ADAM(params(model)) #最適化に使う関数。ここではADAMを使用。
opt = ADAM() #最適化に使う関数。ここではADAMを使用。

学習

さて、次は学習をしてみよう。
まず、ランダムバッチ学習がしたいので、データをランダムバッチにする。以前は、dataは[(x1,y1),(x2,y2),...]という形で入っていたが、今回はバッチとしてdata = [(x,y)]と入れる。つまり、ランダムバッチを作るfunctionは

test.jl
using Random
function make_random_batch(x,y,batchsize)
    numofdata = length(y)
    A = shuffle(1:numofdata)[1:batchsize]
    xdata = x[:,1:batchsize]
    ydata = y[1:batchsize]
    for i=1:batchsize
        xdata[:,i] = x[:,A[i]]
        ydata[i] = y[A[i]]
    end
    data = [(xdata,ydata)]
    return data
end

とする。

実際の学習は、前回の記事とほとんど同じでよくて、

test.jl
function train_batch!(xtest,ytest,model,loss,opt,nt,batchsize)
    for it=1:nt
        data = make_random_batch(xtest,ytest,batchsize) #ランダムバッチを作る
        Flux.train!(loss, params(model),data, opt) #学習
        #Flux.train!(loss, data, opt) #学習
        if it% 100 == 0
            Flux.testmode!(model) #テストモードへ。
            lossvalue = 0.0
            #lossvalue += loss(xtest[:,:],ytest[:]).data #テストデータとの誤差
            lossvalue += loss(xtest[:,:],ytest[:]) #テストデータとの誤差
            println("$(it)-th loss = ",lossvalue)
            Flux.testmode!(model,false) #テストモード終了。
        end
    end
end

である。ここで、テストのデータセットのときには、testmode!を実行してバッチの分散と平均を変更しないようにする必要がある。

最後に、学習の実行と得られた学習パラメータの表示、およびプロットを

test.jl
batchsize =20 #バッチサイズ
nt = 3000 #学習の回数
train_batch!(φ,y0,model,loss,opt,nt,batchsize) #学習

#=
#一層目の学習パラメータ
println(model[1].W.data) #W
println(model[1].b.data) #b

#バッチ正規化層の学習パラメータ
println("β ",model[2].β.data)
println("γ ",model[2].γ.data)
#バッチ正規化層の平均と分散
println("μ ",model[2].μ)
println("σ ",model[2].σ)
#二層目の学習パラメータ
println(model[3].W.data)
println(model[3].b.data)
=#

#一層目の学習パラメータ
println(model[1].W) #W
println(model[1].b) #b

#バッチ正規化層の学習パラメータ
println("β ",model[2].β)
println("γ ",model[2].γ)
#バッチ正規化層の平均と分散
println("μ ",model[2].μ)
println("σ ",model[2].σ²)
#二層目の学習パラメータ
println(model[3].W)
println(model[3].b)

#予測データを作る
Flux.testmode!(model) #テストモードへ。
ye = [model(φ[:,:])[i].data for i=1:length(y0)]#[model(φ[:,i]).data[1] for i=1:length(y0)]
Flux.testmode!(model,false) #テストモード終了

#以下はプロット関連
using Plots
ENV["PLOTS_TEST"] = "true"

pls = plot(x0,[y0[:],ye[:]],marker=:circle,label=["Data","Estimation"])
savefig("comparison_Flux_nn.png")

で得る。

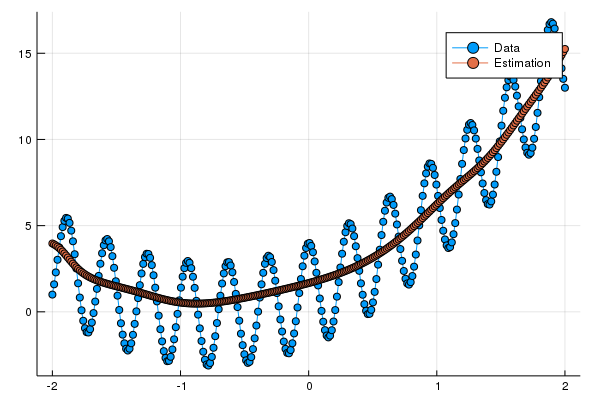
このコードで得られたグラフは

comparison_Flux_nn.png

となっている。実行するたびに乱数が変わり結果も変わる。このモデルでは隠れ層一層のニューラルネットではなく線形補間で十分な感じに見える。

全体のコード

全体のコードは以下のとおりである。

test.jl
n = 300
x0 = range(-2,length=n,stop=2) #Julia 1.0.0以降はlinspaceではなくこの書き方になった。
a0 = 3.0
a1= 2.0
b0 = 1.0
y0 = zeros(Float32,n)
f(x0) = a0.*x0 .+ a1.*x0.^2 .+ b0 .+ 3*cos.(20*x0)
y0[:] = f.(x0)

function make_φ(x0,n,k)
    φ = zeros(Float32,k,n)
    for i in 1:k
        φ[i,:] = x0.^(i-1)
    end
    return φ
end
k = 6
φ = make_φ(x0,n,k)

using Flux
d_input = k
d_middle = 10
d_output = 1
model = Chain(
    Dense(d_input, d_middle,σ), #一層目。活性化関数にシグモイド関数を使用
    BatchNorm(d_middle), #バッチ正規化　
    Dense(d_middle, d_output) #二層目
    )

loss(x, y) =  sum([(y[i] .- model(x)[i]).^2 for i=1:length(y) ])/length(y)
opt = ADAM() #最適化に使う関数。ここではADAMを使用。

using Random
function make_random_batch(x,y,batchsize)
    numofdata = length(y)
    A = shuffle(1:numofdata)[1:batchsize]
    xdata = x[:,1:batchsize]
    ydata = y[1:batchsize]
    for i=1:batchsize
        xdata[:,i] = x[:,A[i]]
        ydata[i] = y[A[i]]
    end
    data = [(xdata,ydata)]
    return data
end

function train_batch!(xtest,ytest,model,loss,opt,nt,batchsize)
    for it=1:nt
        data = make_random_batch(xtest,ytest,batchsize) #ランダムバッチを作る
        Flux.train!(loss, params(model),data, opt) #学習
        if it% 100 == 0
            Flux.testmode!(model) #テストモードへ。
            lossvalue = 0.0
            #lossvalue += loss(xtest[:,:],ytest[:]).data #テストデータとの誤差
            lossvalue += loss(xtest[:,:],ytest[:]) #テストデータとの誤差
            println("$(it)-th loss = ",lossvalue)
            Flux.testmode!(model,false) #テストモード終了。
        end
    end
end

batchsize =20 #バッチサイズ
nt = 3000 #学習の回数
train_batch!(φ,y0,model,loss,opt,nt,batchsize) #学習

#一層目の学習パラメータ
println(model[1].W) #W
println(model[1].b) #b

#バッチ正規化層の学習パラメータ
println("β ",model[2].β)
println("γ ",model[2].γ)
#バッチ正規化層の平均と分散
println("μ ",model[2].μ)
println("σ ",model[2].σ²)
#二層目の学習パラメータ
println(model[3].W)
println(model[3].b)

#予測データを作る
Flux.testmode!(model) #テストモードへ。
ye = [model(φ[:,:])[i] for i=1:length(y0)]#[model(φ[:,i]).data[1] for i=1:length(y0)]
#ye = [model(φ[:,:])[i].data for i=1:length(y0)]#[model(φ[:,i]).data[1] for i=1:length(y0)]
Flux.testmode!(model,false) #テストモード終了

#以下はプロット関連
using Plots
ENV["PLOTS_TEST"] = "true"

pls = plot(x0,[y0[:],ye[:]],marker=:circle,label=["Data","Estimation"])
savefig("comparison_Flux_nn.png")
4
10
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
4
10