この記事は
"Juliaで機械学習:深層学習フレームワークFlux.jlを使ってみる その1:基本編"
https://qiita.com/cometscome_phys/items/e99d6177325e78ebb228
の続きである。
今回は、
"Juliaで機械学習:深層学習フレームワークKnet.jlを使ってみる"
https://qiita.com/cometscome_phys/items/f09e801bc5b3f57f6350
や
"JuliaでTensorFlow その4: 線形基底関数を用いた回帰"
https://qiita.com/cometscome_phys/items/92dba9f82cd58d877ec5
でやったことを、Flux.jlを使ってやってみる。
バージョン
Julia 1.0.0
Flux v0.6.7+ #master
->
Julia 1.1.0
Flux 0.8.3
2019年6月3日追記:Flux.jlがバージョンアップして以下の記事のいくつかは動かなくなっていたようなので、修正。
->
Julia 1.7.3
Flux 0.13.5
2022年9月11日追記:Flux.jlのバージョンアップによって動かなくなっていた箇所を修正。model.Wではなく、model.weightのような形に変更されている。
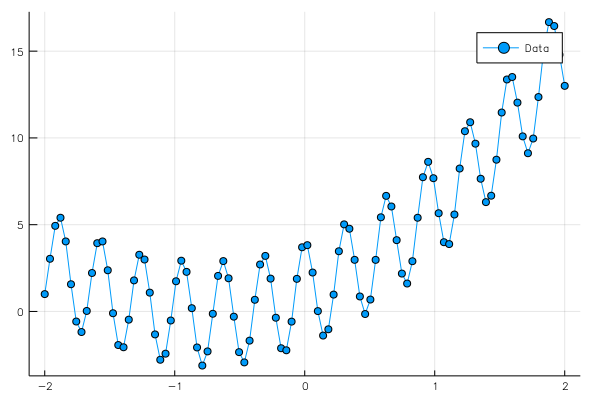
再現すべき関数
これまで書いてきた記事で何度も登場しているが、再掲しておく。
ここでは、ある関数
$$
y = a_0 x+ a_1 x^2 + b_0 + 3\cos(20x)
$$
という関数を考える。ここで、最後のcosはノイズのようなものとして考えており、$a_0$と$a_1$と$b_0$によって得られる二次関数を得ることが目的となる。
データを100点作っておく。
n = 100
x0 = range(-2,length=n,stop=2) #Julia 1.0.0以降はlinspaceではなくこの書き方になった。
a0 = 3.0
a1= 2.0
b0 = 1.0
y0 = zeros(Float32,n)
f(x0) = a0.*x0 .+ a1.*x0.^2 .+ b0 .+ 3*cos.(20*x0)
y0[:] = f.(x0)
グラフは
上のデータをフィッティングする際には、
$$
y = \sum_{k=0}^{k_{\rm max}} a_k x^k + b_0
$$
という形を考える。ここでは、$x^k$を基底関数として線形回帰をしていることになる。
詳しくは、
JuliaでTensorFlow その4: 線形基底関数を用いた回帰
https://qiita.com/cometscome_phys/items/92dba9f82cd58d877ec5
を参照。
インプットデータの生成
ここはこれまでの記事とほとんど同じである。
function make_φ(x0,n,k)
φ = zeros(Float32,k,n)
for i in 1:k
φ[i,:] = x0.^(i-1)
end
return φ
end
k = 4
φ = make_φ(x0,n,k)
データが入ってある引数は配列の一番右であることに注意。ここでは、nがデータの数となるが、PythonでのTensorFlowではこれは一番左の引数であった。PythonのTensorFlowでは、つまり、行列とベクトルの積を$x W$と書いていた。
つまり、今回はKnetの時と同じである。
モデルの構築
モデルを構築する。
その1でも述べたように、Flux.jlでは、簡単な書き方ができる。今回は線形回帰なので、インプット数がk、アウトプット数が1であり、
using Flux
model = Dense(k, 1) #モデルの生成。W*x + b : W[1,k],b[1]
でよい。
このDenseにはW(weight)とb(bias)が含まれている。アクセスするためには、
println("W = ",model.weight)
println("b = ",model.bias)
とすればよい。
次に、最小化するべきloss関数を定義するには
loss(x, y) = Flux.mse(model(x), y) #loss関数。mseは平均二乗誤差
とすればよい。ここで、mseは平均二乗誤差である。もちろん、他の関数に変えることもできる。
次に、最適化に使う関数を
opt = ADAM() #最適化に使う関数。ここではADAMを使用。
で定義しておく。
学習
さて、次は学習をしてみよう。
まず、ランダムバッチ学習がしたいので、データをランダムバッチにする:
function make_random_batch(x,y,batchsize)
numofdata = length(y)
A = rand(1:numofdata,batchsize) #インデックスをシャッフル
data = []
for i=1:batchsize
push!(data,(x[:,A[i]],y[A[i]])) #ランダムバッチを作成。 [(x1,y1),(x2,y2),...]という形式
end
return data
end
Fluxでは、データは[(x1,y1),(x2,y2),...]という形式で、xにインプットデータの配列、yにアウトプットデータの配列が入り、それがタプルで対になっている。
この関数では、ランダムにbatchsize個データを取ってきている。
学習は
function train_batch!(xtest,ytest,model,loss,opt,nt)
for it=1:nt
data = make_random_batch(xtest,ytest,batchsize)
Flux.train!(loss, Flux.params(model),data, opt)
if it% 100 == 0
lossvalue = 0.0
for i=1:length(ytest)
lossvalue += loss(xtest[:,i],ytest[i])
end
println("$(it)-th loss = ",lossvalue/length(y0))
end
end
end
batchsize = 20
nt = 2000
train_batch!(φ,y0,model,loss,opt,nt) #学習
println(model.weight) #W
println(model.bias) #b
#Wとbを使って予測値を作る。
ye = [model(φ[:,i])[1] for i=1:length(y0)]
#以下はプロット。
using Plots
ENV["PLOTS_TEST"] = "true"
pls = plot(x0,[y0[:],ye[:]],marker=:circle,label=["Data" "Estimation"])
savefig("comparison_Flux.png")
plot(x0,[y0[:],ye[:]],marker=:circle,label=["Data" "Estimation"])
とすればよい。ここでは、nt回ランダムバッチを作って、その度にWとbをADAMを用いて変化させている。
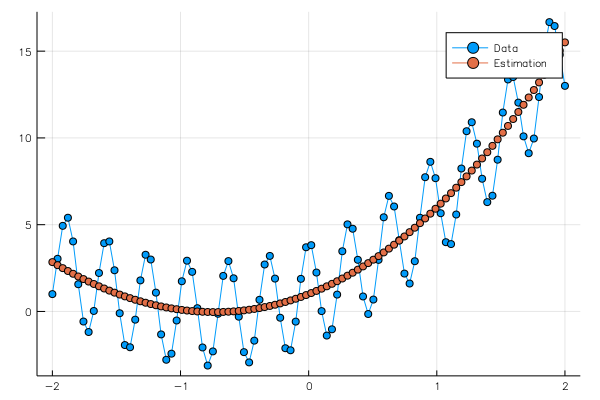
学習の結果、
Float32[0.1877329 3.0070586 2.0609143 -0.017856542]
Float32[0.73010457]
という重みとバイアスが得られ、グラフは、
となる。
#全体のコード
全体のコードは、
n = 100
x0 = range(-2,length=n,stop=2) #Julia 1.0.0以降はlinspaceではなくこの書き方になった。
a0 = 3.0
a1= 2.0
b0 = 1.0
y0 = zeros(Float32,n)
f(x0) = a0.*x0 .+ a1.*x0.^2 .+ b0 .+ 3*cos.(20*x0)
y0[:] = f.(x0)
function make_φ(x0,n,k)
φ = zeros(Float32,k,n)
for i in 1:k
φ[i,:] = x0.^(i-1)
end
return φ
end
k = 4
φ = make_φ(x0,n,k)
using Flux
model = Dense(k, 1) #モデルの生成。W*x + b : W[1,k],b[1]
println("W = ",model.weight)
println("b = ",model.bias)
loss(x, y) = Flux.mse(model(x), y) #loss関数。mseは平均二乗誤差
opt = ADAM() #最適化に使う関数。ここではADAMを使用。
function make_random_batch(x,y,batchsize)
numofdata = length(y)
A = rand(1:numofdata,batchsize)
data = []
for i=1:batchsize
push!(data,(x[:,A[i]],y[A[i]])) #ランダムバッチを作成。 [(x1,y1),(x2,y2),...]という形式
end
return data
end
function train_batch!(xtest,ytest,model,loss,opt,nt)
for it=1:nt
data = make_random_batch(xtest,ytest,batchsize)
Flux.train!(loss, Flux.params(model),data, opt)
if it% 100 == 0
lossvalue = 0.0
for i=1:length(ytest)
lossvalue += loss(xtest[:,i],ytest[i])
end
println("$(it)-th loss = ",lossvalue/length(y0))
end
end
end
batchsize = 20
nt = 2000
train_batch!(φ,y0,model,loss,opt,nt) #学習
println(model.weight) #W
println(model.bias) #b
#Wとbを使って予測値を作る。
ye = [model(φ[:,i])[1] for i=1:length(y0)]
#以下はプロット。
using Plots
ENV["PLOTS_TEST"] = "true"
pls = plot(x0,[y0[:],ye[:]],marker=:circle,label=["Data" "Estimation"])
savefig("comparison_Flux.png")
plot(x0,[y0[:],ye[:]],marker=:circle,label=["Data" "Estimation"])
となる。
なお、modelを変えれば容易に多層ニューラルネットワークを作ることができる。
今の所、Knet.jlよりもFlux.jlの方が扱いやすいかもしれない。