これまで、JuliaでTensorFlowを使った機械学習についてまとめてきた。
今回は、
Juliaで使える深層学習フレームワークKnet(カイネットと発音するらしい)を使ってみる。
https://github.com/denizyuret/Knet.jl
JuliaでTensorFlow.jlを使った記事
"JuliaでTensorFlow その4: 線形基底関数を用いた回帰"
https://qiita.com/cometscome_phys/items/92dba9f82cd58d877ec5
でやったことを、Knet.jlを使ってやってみる。
利点
- 速いらしい
- GPUも使えるらしい
- Pythonを使わずにJuliaだけで書ける
欠点
- 文献が日本語英語含めてほとんどない
バージョン
Julia 0.6.2
Knet 0.9.0
再現すべき関数
これまで書いてきた記事で何度も登場しているが、再掲しておく。
ここでは、ある関数
$$
y = a_0 x+ a_1 x^2 + b_0 + 3cos(20x)
$$
という関数を考える。ここで、最後のcosはノイズのようなものとして考えており、$a_0$と$a_1$と$b_0$によって得られる二次関数を得ることが目的となる。
データを100点作っておく。
n = 100
x0 = linspace(-2,2,n)
a0 = 3.0
a1= 2.0
b0 = 1.0
y0 = zeros(Float32,(1,n))
f(x0) = a0.*x0 + a1.*x0.^2 + b0 + 3*cos.(20*x0)
y0[:] = f(x0)
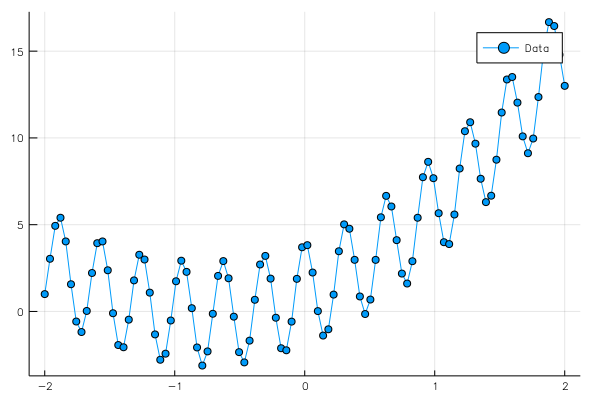
グラフは
上のデータをフィッティングする際には、
$$
y = \sum_{k=0}^{k_{\rm max}} a_k x^k + b_0
$$
という形を考える。ここでは、$x^k$を基底関数として線形回帰をしていることになる。
詳しくは、
JuliaでTensorFlow その4: 線形基底関数を用いた回帰
https://qiita.com/cometscome_phys/items/92dba9f82cd58d877ec5
を参照。
インプットデータの生成
ここはこれまでの記事とほとんど同じである。
function make_φ(x0,n,k)
φ = zeros(Float32,k,n)
for i in 1:k
φ[i,:] = x0.^(i-1)
end
return φ
end
k = 4
φ = make_φ(x0,n,k)
データが入ってある引数は配列の一番右であることに注意。ここでは、nがデータの数となるが、PythonでのTensorFlowではこれは一番左の引数であった。PythonのTensorFlowでは、つまり、行列とベクトルの積を$x W$と書いていた。
Knetでは、よく見られる形である$W x$の形式で書くことにする。
モデルの構築
次に、モデルを構築する。Knetでは、学習すべき量はwと書き、リスト形式で全てを持つようにするようだ。
今回は、重み$W$とバイアス$b$がある。$W$は$1 \times k$の行列である。よって、学習すべき量を
w = Any[ones(Float32,(1,k)),ones(Float32,1)]
とする。一つ目が重み、二つ目がバイアスとなる。
次に、このwを使って、値を予言するための関数:
function predict(w,x)
y = w[1]*x .+w[2]
return y
end
を作る。TensorFlowではここにグラフの構築が入っていた。
さらに、loss関数を
loss(w,x,y) = mean(abs2,y-predict(w,x))
その勾配を
lossgradient = grad(loss)
と定義しておく。
Knetでは、計算した勾配からwをアップデートする関数update!が用意されており、
トレーニングは
function train(model, data, optim)
for (x,y) in data
grads = lossgradient(model,x,y)
update!(model, grads, optim)
end
end
と書くことができる。ここで、optimは最適化のための関数で、今回はAdamを使うことにする。
このtrainを繰り返し呼ぶことで学習が進む。
学習
さて、学習をしてみよう。一つ一つデータを入れて学習させてもよいが、やはりランダムバッチ学習がしたい。
そこで、minibatch関数を使って、
dtrn = minibatch(φ,y0,10,shuffle=true)
としてみよう。ここでは、10個ランダムにデータを取ってきている。
具体的な学習のプロセスは
o = optimizers(w, Adam)
for i in 1:2000
train(w,dtrn,o)
if i%100 == 0
println(loss(w,φ,y0))
end
end
で実行できる。ここで、最適化にAdamを使うため、optimizers(w, Adam)を呼んだ。
全体のコードは
n = 100
x0 = linspace(-2,2,n)
a0 = 3.0
a1= 2.0
b0 = 1.0
y0 = zeros(Float32,(1,n))
f(x0) = a0.*x0 + a1.*x0.^2 + b0 + 3*cos.(20*x0)
y0[:] = f(x0)
function make_φ(x0,n,k)
φ = zeros(Float32,k,n)
for i in 1:k
φ[i,:] = x0.^(i-1)
end
return φ
end
k = 4
φ = make_φ(x0,n,k)
w = Any[ones(Float32,(1,k)),ones(Float32,1)]
function predict(w,x)
y = w[1]*x .+w[2]
return y
end
loss(w,x,y) = mean(abs2,y-predict(w,x))
lossgradient = grad(loss)
function train(model, data, optim)
for (x,y) in data
grads = lossgradient(model,x,y)
update!(model, grads, optim)
end
end
dtrn = minibatch(φ,y0,10,shuffle=true)
o = optimizers(w, Adam)
for i in 1:2000
train(w,dtrn,o)
if i%100 == 0
println(loss(w,φ,y0))
end
end
ye = predict(w,φ)
using Plots
ENV["PLOTS_TEST"] = "true"
pls = plot(x0,[y0[1,:],ye[1,:]],marker=:circle,label=["Data","Estimation"])
savefig("comparison_2.png")
となる。
学習の結果、
Any[Float32[0.481912 2.94451 2.05044 0.0198765], Float32[0.481912]]
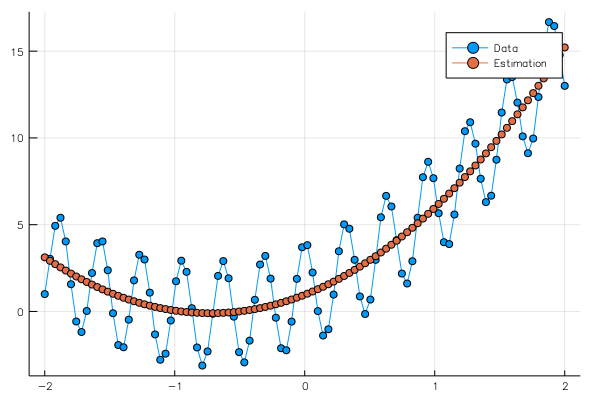
という重みとバイアスが得られ、グラフは
となる。