「Deep Learning」という本（著者 Ian Goodfellow / Yoshua Bengio / Aaron Courville。まもなく日本語訳が出版されるらしい。以下、この本をGYCと呼ぶ）はとても分かりやすい。この本の6.1節で、XORを扱っている。これにヒントを得て、順伝播型ニューラルネットワーク（Feedforward Neural Network）を使って、XORを含むいくつかの論理演算を実現する。
これは、とてもつまらない問題だ。機械学習を行うわけではない。表題に実装という言葉を使ったが、条件を満たすネットワーク構造（変換行列）を頭の中で考えるだけである。しかし、ちょっと面白い。簡単な論理演算をNeural Network（以下ではNNと略する）上に展開することは、NNの理解の大きな助けになる。
問題の定義
規則
ここで、規則を決めておく。
- 2個のブール値を$a$、$b$としたとき、2項演算 $c = a \bigtriangleup b$ を求めるのが目的である
- ブール値を実数の{0, 1}で表現する
- 各層は、前の層に線形変換とバイアス付加を施したのち、活性化関数を施して導出する
- 活性化関数はReLU関数を用いる
- 複数の解があるときは、層の数が少ない方を正解とする
ここで、活性化関数としてReLU関数
$$ ReLU(x) = max(0, x) $$
を用いたのは、シグモイド関数などを用いるのに比べて、演算結果を正確に{0, 1}に一致させることが出来るからである。隠れ層の活性化関数としては、一般にReLU関数が最も優れているとも言われている。
アフィン変換
線形変換$w$とバイアス$\boldsymbol{b}$を別々に表わすのは煩雑なので、アフィン変換行列$W$で表現する（正確に言うと、アフィン変換ではなくアフィン写像）。すなわち、
$$ \boldsymbol{x}w + \boldsymbol{b} = (\boldsymbol{x}\,\, 1)W = \tilde{\boldsymbol{x}}W$$
である。ここで、入力$x$は左側から作用させている。そのため、$\boldsymbol{x}$も$\boldsymbol{b}$も行ベクトルである。これは、TensorFlowの演算に合せたからである。また、$\tilde{\boldsymbol{x}}$は、$\boldsymbol{x}$を拡張して定数1の成分を加えたベクトルである。
アフィン変換行列 $W$ は形式的に、
$$ W = \left( \begin{array}{c|c} w & 0 \\ \hline \boldsymbol{b} & 1 \end{array} \right) $$
と表せる。要素で表すと、$w$を$n \times m$行列としたとき、
$$ W_{ij} = \left\{ \begin{array}{cl} w_{ij} & (i<=n, j<=m) \\ b_j & (i=n+1, j<=m) \\ 0 & (i<=n, j=m+1) \\ 1 & (i=n+1, j=m+1) \end{array} \right.$$
である。入力ベクトルを左から作用させるため、通常のアフィン変換を転置した形になっている。これにより、$k+1$層 の拡大ベクトル $\tilde{\boldsymbol{x}}_{k+1}$ は、
$$ \tilde{\boldsymbol{x}}_{k+1} = g_{k+1}(\tilde{\boldsymbol{x}}_{k}W_{k+1})$$
と表せる。ここで、$g_{k+1}$ は$ReLU$関数である。出力層の場合は、活性化関数が必要ない場合（$g()=1()$）もある。
入力
2個のブール値{0, 1}の演算のパターンは4通りしかない。従って、その4通りの結果を再現できれば正解である。その4通りをまとめて入力とすると（入力パターンを新たな次元とした）
$$ \boldsymbol{x}_{0} = \left( \begin{array}{cc} 1 & 1 \\ 1 & 0 \\ 0 & 1 \\ 0 & 0 \end{array}\right) \tag{1}$$
と表すことができる。アフィン変換のために(1)を拡大book:したベクトルは
$$ \tilde{\boldsymbol{x}}_{0} = \left( \begin{array}{ccc} 1 & 1 & 1\\ 1 & 0 & 1\\ 0 & 1 & 1\\ 0 & 0 & 1\end{array}\right)$$
である。
論理演算
XOR
GYCにならってXORを考える。入力 $(1)$ に対して、XORの出力は、
$$ \boldsymbol{x}_{N-1} = \left( \begin{array}{c} 0 \\ 1 \\ 1 \\ 0 \end{array} \right) \tag{2}$$
とならなければならない（$N$は層の数）。
GYCの6.1節では、XORを隠れ層を1つ含む3層で実現している。GYCの結果をアフィン行列で表すと
$$ W_1 = \left( \begin{array}{ccc} 1 & 1 & 0 \\ 1 & 1 & 0 \\ 0 & -1 & 1 \end{array} \right), \quad W_2 = \left( \begin{array}{c} 1 & 0 \\ -2 & 0 \\ 0 & 1 \end{array} \right) \tag{3}$$
と表される。なお、活性化は出力層（第2層）には施さない。この過程を具体的に見てみよう。まず、入力に$W_1$とReLU関数を作用させると、
$$ \tilde{\boldsymbol{x}}_{1} = ReLU(\left( \begin{array}{ccc} 1 & 1 & 1\\ 1 & 0 & 1\\ 0 & 1 & 1\\ 0 & 0 & 1\end{array}\right) \left( \begin{array}{ccc} 1 & 1 & 0 \\ 1 & 1 & 0 \\ 0 & -1 & 1 \end{array} \right)) = ReLU(\left( \begin{array}{ccc} 2 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 0 & 1 \\ 0 & -1 & 1 \end{array} \right)) = \left( \begin{array}{ccc} 2 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 0 & 1 \\ 0 & 0 & 1 \end{array} \right) $$
次に、$W_2$を作用させると、
$$ \tilde{\boldsymbol{x}}_{2} = \left( \begin{array}{ccc} 2 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 0 & 1 \\ 0 & 0 & 1 \end{array} \right) \left( \begin{array}{cc} 1 & 0 \\ -2 & 0 \\ 0 & 1 \end{array} \right) = \left( \begin{array}{cc} 0 & 1 \\ 1 & 1 \\ 1 & 1 \\ 0 & 1 \end{array} \right)$$
上式の定数成分である第2列を取り除けば、式(2)が得られる（$N=3$）。
ところで、XORには別の解がある。それは、
$$ W_1 = \left( \begin{array}{ccc} 1 & -1 & 0 \\ -1 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right), \quad W_2 = \left( \begin{array}{c} 1 & 0 \\ 1 & 0 \\ 0 & 1 \end{array} \right) \tag{4}$$
である。(4)の別解の方が、GYCの解(3)より少し簡単な形をしているので（バイアスベクトルがゼロである）、実際に使うときには便利だろう。これが解になることは、みなさんに確かめてもらいたい。
論理演算の表
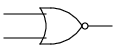
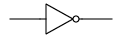
以上のようにして求められた基本的な論理演算について、変換行列を以下の表にまとめる（これが最適な解とは限らない。もっと良い解があれば教えて頂きたい）。論理回路の回路記号も示す（後の記事で使用する）。
| 演算 | $W_1$ | $W_2$ | 出力 | 回路記号 |
|---|---|---|---|---|
| AND | $\left( \begin{array}{cc} 1 & 0 \\ 1 & 0 \\ -1 & 1 \end{array} \right)$ | - | $\left( \begin{array}{c} 1 \\ 0 \\ 0 \\ 0 \end{array} \right)$ |  |
| OR | $\left( \begin{array}{cc} -1 & 0 \\ -1 & 0 \\ 1 & 1 \end{array} \right)$ | $\left( \begin{array}{c} -1 & 0 \\ 1 & 1 \end{array} \right)$ | $\left( \begin{array}{c} 1 \\ 1 \\ 1 \\ 0 \end{array} \right)$ |  |
| XOR | $\left( \begin{array}{ccc} 1 & -1 & 0 \\ -1 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right)$ | $\left( \begin{array}{c} 1 & 0 \\ 1 & 0 \\ 0 & 1 \end{array} \right)$ | $\left( \begin{array}{c} 0 \\ 1 \\ 1 \\ 0 \end{array} \right)$ |  |
| NAND | $\left( \begin{array}{cc} 1 & 0 \\ 1 & 0 \\ -1 & 1 \end{array} \right)$ | $\left( \begin{array}{c} -1 & 0 \\ 1 & 1 \end{array} \right)$ | $\left( \begin{array}{c} 0 \\ 0 \\ 0 \\ 1 \end{array} \right)$ |  |
| NOR | $\left( \begin{array}{cc} -1 & 0 \\ -1 & 0 \\ 1 & 1 \end{array} \right)$ | - | $\left( \begin{array}{c} 0 \\ 1 \\ 1 \\ 1 \end{array} \right)$ |  |
| NXOR | $\left( \begin{array}{ccc} 1 & -1 & 0 \\ -1 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right)$ | $\left( \begin{array}{c} -1 & 0 \\ -1 & 0 \\ 1 & 1 \end{array} \right)$ | $\left( \begin{array}{c} 1 \\ 0 \\ 0 \\ 1 \end{array} \right)$ |  |
| NOT | $\left( \begin{array}{c} -1 & 0 \\ 1 & 1 \end{array} \right)$ | - | $\left(\begin{array}{cc} 0 \\ 1\end{array}\right)$ |  |
ここで、活性化関数$g_1$は全てReLU関数であり（NOTを除く）、$g_2$は1（活性化しない）である。NOTは単項演算子なので、この場合だけ入力として$\left(\begin{array}{cc} 1 \\ 0\end{array}\right)$を使用している。また、XORにはGYCではなく(4)式の別解の方を示してある。
AND / NORは隠れ層なしの2層だけで表現できるが、OR / NANDには3層が必要であることに注意してほしい。これは、活性化関数にReLU関数を使っていることによる特徴である。
カウンタ
これだけでは面白くないので、上の表を使ってカウンタを実装してみたい（これを、実装と言うのだろうか？）。答えは別の記事（「Neural Networkでカウンタを実装する」）にするが、ここで問題の要件だけを提示しておく。興味のある方は考えていただきたい。複数の実装があるが、最も層の数が少ないものを正解とする。
- 1ビットのカウンタ
- 入力は、信号ビットとカウンタビット
- 出力は、桁上り信号ビットとカウンタビット
- 信号ビットが0ならば、カウンタビットは変化せず、桁上りビットは0
- 信号ビットが1で、カウンタビットが0ならば、出力カウンタビットは1、桁上りビットは0
- 信号ビットが1で、カウンタビットが1ならば、出力カウンタビットは0、桁上りビットは1
これをまとめると、次のようになる。$\boldsymbol{x}_{0}$が入力、$\boldsymbol{x}_{N-1}$が出力である。
$$ \boldsymbol{x}_{0} = \left( \begin{array}{cc} 0 & 0 \\ 0 & 1 \\ 1 & 0 \\ 1 & 1 \end{array} \right), \quad \boldsymbol{x}_{N-1} = \left( \begin{array}{cc} 0 & 0 \\ 0 & 1 \\ 0 & 1 \\ 1 & 0 \end{array} \right) $$
ここで、第1列が信号/桁上りビットであり、第2列がカウンタビットである。
変更履歴
- カウンタを作成する問題の解答となる記事を作成して、この記事内にリンクを張った