この記事は現代化学(東京化学同人)の2022年4月号から2024年3月号まで連載された安藤耕司先生の「Pythonによる化学シミュレーション入門」を読んでやってみた記事です。詳しい内容は上記の「Pythonによる化学シミュレーション入門」をご参照ください。今回は、2024年1月号の分子軌道法(4)と2024年2月号の分子軌道法(5)の内容です。
直鎖pi共役系炭化水素の分子軌道の簡易表示
Hückel法は、$\pi$電子のみを考慮した分子軌道法です。以前の記事の通り、Hückel法ではSchrödinger方程式を近似的に解くことで、分子軌道のエネルギーやその電子密度や位相を求めることができました。直鎖の$\pi$共役系炭化水素では、炭素の$2p$軌道の電子が$\pi$電子となります。炭素の位置に大きさが電子密度に依存し、色が位相に対応した$2p_z$軌道を図示することで、Hückel法で求められる分子軌道の形を見てみましょう。
プログラムと結果
先にプログラムの全体と結果を示します。このプログラムを動かすと「Enter N:」と聞いてくるので直鎖の$\pi$共役系炭化水素の炭素数を入力してください。以下に4を入力して1,3-ブタジエンの結果を示します。
import numpy as np
import matplotlib.pyplot as plt
N = int(input("Enter N: "))
def mollinear(N):
dx = np.cos(np.pi/6)
dy = np.sin(np.pi/6)
mol = []
for i in range(N):
mol.append([i*dx, (i%2)*dy, 0])
mol = np.array(mol)
mol -= np.mean(mol, axis=0)
return mol
def mollinear_huckel_hamiltonian(N):
H = np.zeros((N,N))
for i in range(N):
if i + 1 < N:
H[i, i + 1] = 1
H[i + 1, i] = 1
if i - 1 >= 0:
H[i, i - 1] = 1
H[i - 1, i] = 1
return H
ngrid = 32
theta = np.linspace(0, np.pi, ngrid)
phi = np.linspace(0, 2*np.pi, ngrid)
theta, phi = np.meshgrid(theta, phi)
xyz = np.array([np.sin(theta)*np.cos(phi),
np.sin(theta)*np.sin(phi),
np.cos(theta)])
Y = np.cos(theta)
Yx, Yy, Yz = np.abs(Y)*xyz
cmap = plt.cm.ScalarMappable(cmap=plt.get_cmap("bwr"))
fasecols = cmap.to_rgba(Y)
def surf2pz(coef, atomcen):
x = coef*Yx + atomcen[0]
y = coef*Yy + atomcen[1]
z = coef*Yz + atomcen[2]
return x,y,z
def plotorb3d(c, mol):
fig = plt.figure()
ax = fig.add_subplot(projection="3d")
ax.grid('False')
N = len(mol)
for i in range(N-1):
for j in range(i+1, N):
if np.linalg.norm(mol[i] - mol[j]) < 1.1:
x,y,z = np.array([mol[i], mol[j]]).T
ax.plot(x, y, z, 'o-', color="gray",linewidth=5)
resale, limscale = 2.5, 1.8
for i in range(N):
x, y, z = surf2pz(resale*c[i], mol[i])
surf = ax.plot_surface(x, y, z, facecolors=fasecols)
surf.set_facecolor((0,0,0,0))
xylim = np.max(np.abs(mol))*limscale
ax.set_xlim(-xylim, xylim)
ax.set_ylim(-xylim, xylim)
ax.set_zlim(-xylim, xylim)
plt.show()
mol = mollinear(N)
H = mollinear_huckel_hamiltonian(N)
if N%2 == 0:
nocc = int(N/2)
nvac = N - nocc
occ = [2]*nocc + [0]*nvac
elif N%2 == 1:
nocc = int((N-1)/2)
nvac = N - nocc
occ = [2]*nocc + [1] + [0]*nvac
ee, cc = np.linalg.eigh(H)
for i in range(len(mol)):
c = cc.T[:,i]
plotorb3d(c, mol)
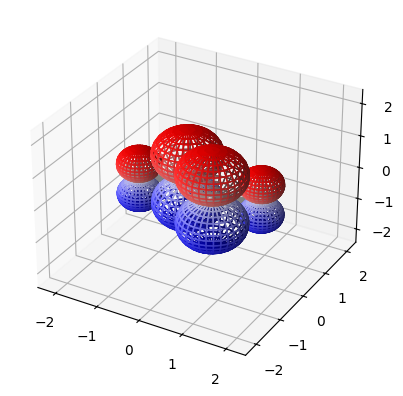
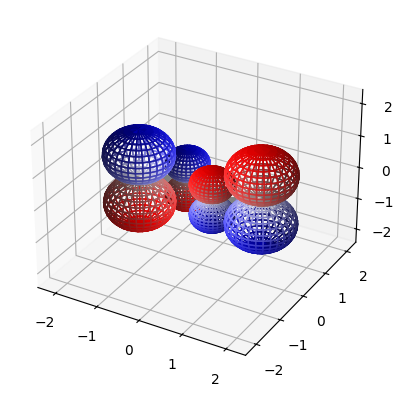
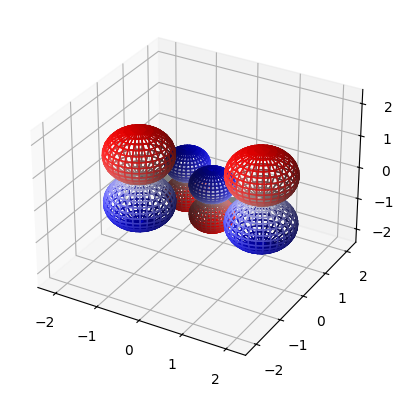
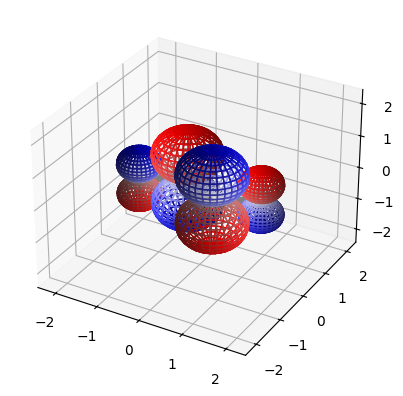
ここから出図の結果です。
最初から順番に見ていくと、節の数がどんどん増えていくのがわかります。なので一枚目の分子軌道が安定な軌道$\psi_1$で、最後の分子軌道が一番エネルギーの高い軌道$\psi_4$になります。
プログラムの概要
mollinear
直鎖の共役炭化水素の原子位置を生成しています。共役炭化水素の炭素は全て同一平面状にいて、全ての炭素で120$^{\circ}$折れ曲がっていると仮定して、xy平面上に原子位置を生成しています。
mollinear_huckel_hamiltonian
直鎖の共役炭化水素のハミルトニアン行列を生成しています。これの固有値問題をnp.linalg.eighで解くことで分子軌道の情報が得られます。
plotorb3d
大きさが電子密度に依存し、色が位相に対応した$2p_z$軌道をぞれぞれの炭素の位置に図示しています。
結果の検討
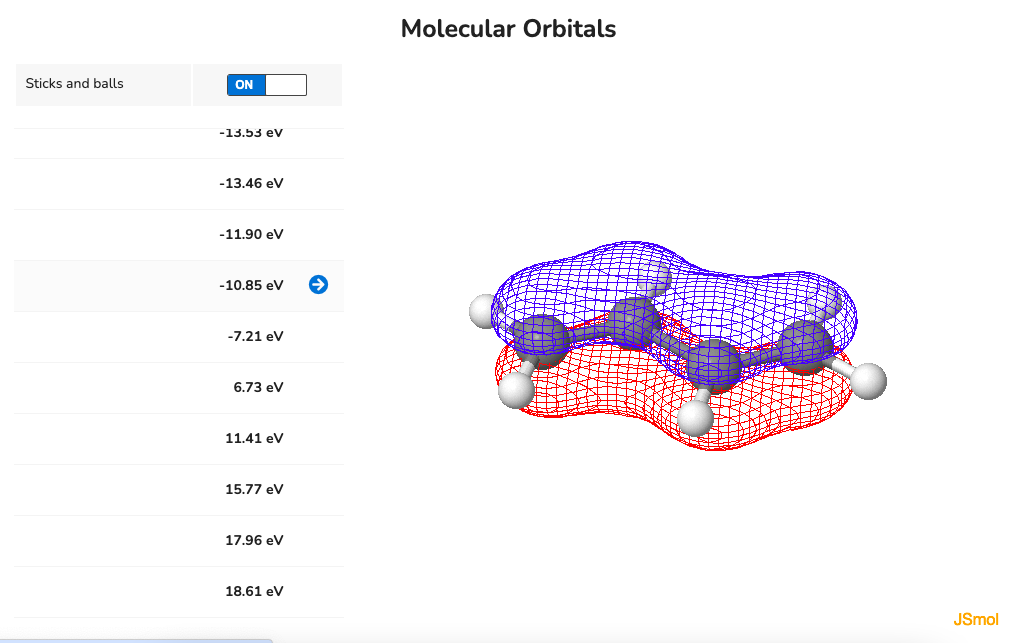
今回プロットしてみた結果が合っているのかどうかを他のアプリケーションを使った計算結果と比較します。比較するのはMolCalcという教育用の量子化学計算アプリケーションです。MolCalcで1,3-ブタジエンの量子化学計算を行い、先ほどの、$\psi_1$から$\psi_4$に対応する分子軌道を示します。
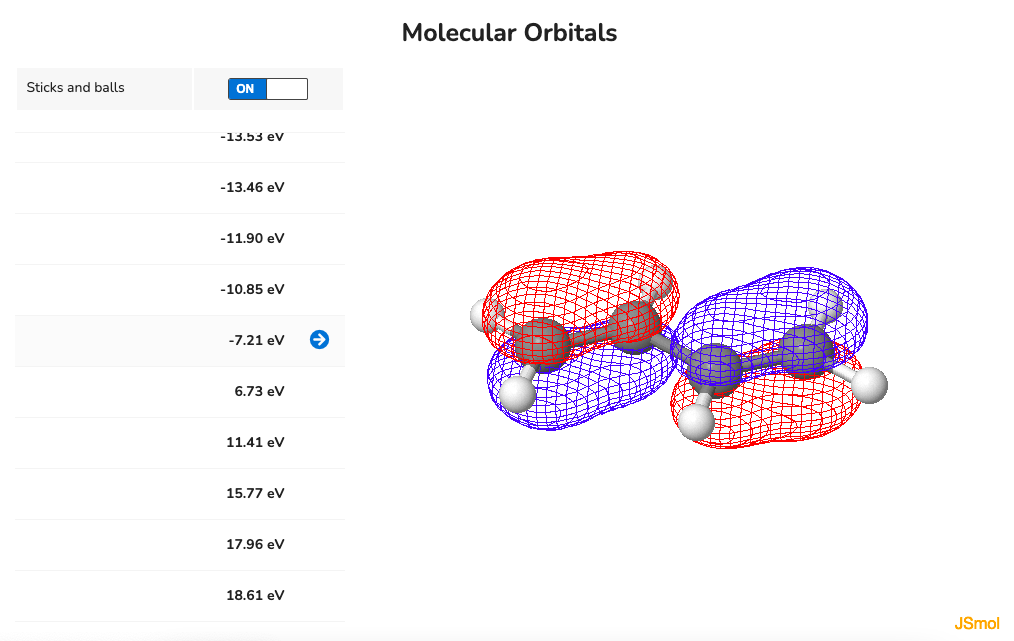
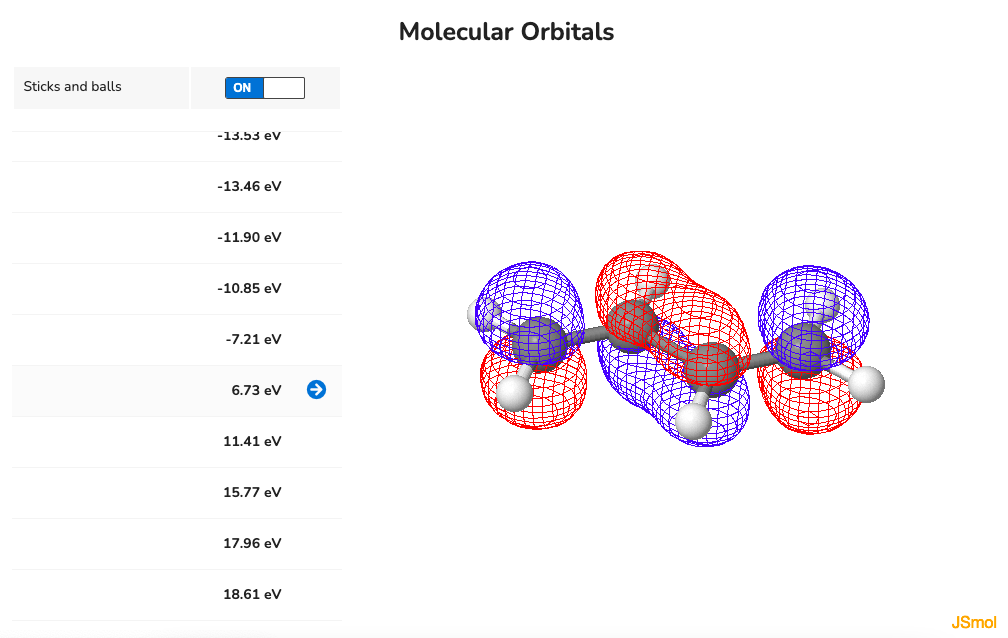
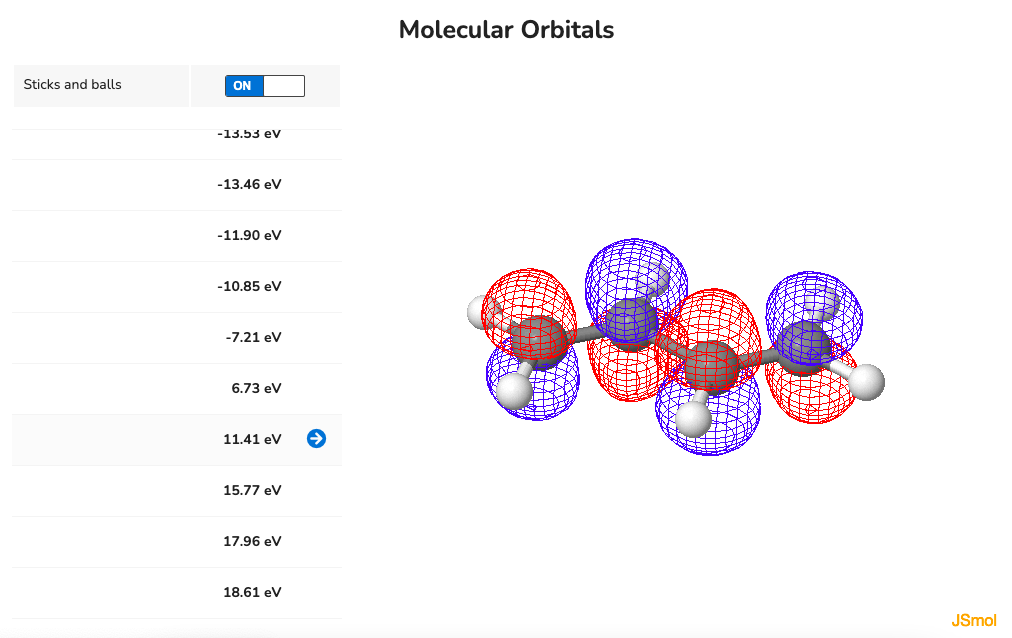
最初から順番に見ていくと、pythonでプロットしたものと同様に、節の数がどんどん増えていくのがわかります。なので一枚目の分子軌道が安定な軌道$\psi_1$で、最後の分子軌道が一番エネルギーの高い軌道$\psi_4$に対応します。pythonでプロットしたものとの大きな違いは、位相が同じで隣り合う電子軌道同士が繋がっているところです。実際は節で隔てられていない軌道同士は繋がるんだと思います。MolCalcでは軌道のエネルギーも算出されていて$\psi_1$、$\psi_2$、$\psi_3$、$\psi_4$がそれぞれ-10.85、-7.21、6.73、11.41 eVになっています。$\psi_1$と$\psi_2$は軌道のエネルギーが負なので結合性軌道、$\psi_3$と$\psi_4$は軌道のエネルギーが正なので反結合性軌道だとわかります。中性の基底状態の1,3-ブタジエン分子においては$\psi_2$まで電子が占有しており、これがHOMO(最高被占軌道)になります。$\psi_1$がHOMO-1、$\psi_2$がHOMO、$\psi_3$がLUMO(最低空軌道)、$\psi_4$がLUMO+1と呼ばれる軌道になります。HOMOとLUMOを合わせてフロンティア軌道と呼びます。フロンティア軌道の電子は化学反応や物性に関わる重要な電子です。Hückel法は$\pi$電子のみを考慮した分子軌道法で、計算は簡便ですが、内殻電子を考慮しません。それでも、Hückel法は、1,3-ブタジエンのような分子においてはフロンティア軌道を記述できることがわかります。
連載記事目次
・「Pythonによる化学シミュレーション入門」をやってみたよ~単分子一次反応の反応速度論~
・「Pythonによる化学シミュレーション入門」をやってみたよ2~色々な反応の反応速度~
・「Pythonによる化学シミュレーション入門」をやってみたよ3~振動反応~
・「Pythonによる化学シミュレーション入門」をやってみたよ4~ランダムウォークと拡散現象~
・「Pythonによる化学シミュレーション入門」をやってみたよ5~ブラウン運動とランジュバン方程式~