「Pythonによる化学シミュレーション入門」をやってみたよ7~Hückel法とフロンティア軌道理論~

この記事は現代化学(東京化学同人)の2022年4月号から2024年3月号まで連載された安藤耕司先生の「Pythonによる化学シミュレーション入門」を読んでやってみた記事です。詳しい内容は上記の「Pythonによる化学シミュレーション入門」をご参照ください。今回は、2023年11月号の分子軌道法(2)と2023年12月号の分子軌道法(3)の内容です。

やること

前回の続き。
Hückel法を用いたナフタレンの求電子置換反応の位置選択性の予測

Hückel法のおさらい

Hückel法では、分子軌道$\psi_i$を、その分子を構成する各原子軌道$\chi_p$の線型結合で表されるとする、LCAO近似を用いて、次のように表します。

$$
\psi_i = \Sigma^N_p c_{pi} \chi_p
$$

この分子の原子数は$N$です。$c_{pi}$はi番目の分子軌道へのp番目の原子軌道の寄与であり、Hückel法では、固有関数がLCAO近似で表現される分子軌道$\psi_i$、演算子がハミルトニアン行列の固有値問題を解くことで、軌道のエネルギーである固有値$E$を求めます。

電子分布と結合次数

ここで、原子軌道$\chi_p$と$\chi_r$の結合次数$\mu$を次のように定義します。

$$
\mu_{pr} = \Sigma^N_p f_i c_{pi} c^*_{ri}
$$

$f_p$は、i番目の分子軌道$\psi_i$の電子占有数です。電子占有数は各分子軌道を占有する電子数を表したもので、基底状態のエチレンでは$f_i = [2, 0]$です。アリルカチオン(CH$_2$=CHCH$_2^+$)では$f_i = [2, 0, 0]$、アリルラジカル(CH$_2$=CHCH$_2 \cdot$)では$f_i = [2, 1, 0]$となるでしょう。

次に、原子軌道$\chi_p$の電子密度を次のように定義します。

$$
q_p = \mu_{pp} =\Sigma^N_p f_p |c_{pi}|^2
$$

要素が$\mu_{pr}$となる行列を密度行列と言います。

ハミルトニアン行列の生成

Hückel法では、固有関数がLCAO近似で表現される分子軌道$\psi_i$、演算子がハミルトニアン行列の固有値問題を解くことで、軌道のエネルギーである固有値$E$を求めます。このハミルトニアン行列を、結合した炭素の組を与えることで生成するプログラムを作りましょう。

ここで、Hückel法では一般に固有値$E$はクーロン積分$\alpha$に共鳴積分$\beta$の定数倍を足し引きした形($E=\alpha \pm c \beta$)になります。そこで、エネルギーの原点を$\alpha$、単位を$\beta$にして計算することにすれば、ハミルトニアン行列中のクーロン積分と共鳴積分は$\alpha = 0$、$\beta = 1$で良いでしょう。

def huckel_hamiltonian(N, bonds):
  H = np.zeros((N,N))
  for (i, j) in bonds:
    H[i-1,j-1] = 1
    H[j-1,i-1] = 1
  print(H)
  return H 

ハミルトニアン行列の生成をhuckel_hamiltonianという関数にしときました。このハミルトニアン行列の固有関数を固有値を求めれば、分子軌道$\psi_i$のエネルギー$E$とその時の$c_{pi}$を決定できます。固有値問題はnumpyのlinalg.eighを使って解きます。以下いくつか例を解いてみます。

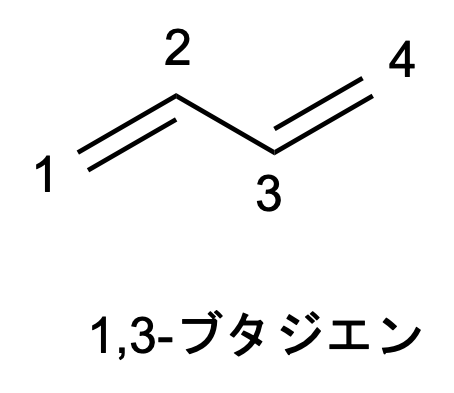
例１）1,3-ブタジエン

import numpy as np
H = huckel_hamiltonian(4, [(1,2), (2,3), (3,4)])

ee, cc = np.linalg.eigh(H)
print(ee.round(4))
print(cc.round(4))

出力結果は以下になります。

[[0. 1. 0. 0.]
 [1. 0. 1. 0.]
 [0. 1. 0. 1.]
 [0. 0. 1. 0.]]
[-1.618 -0.618  0.618  1.618]
[[ 0.3717  0.6015  0.6015  0.3717]
 [-0.6015 -0.3717  0.3717  0.6015]
 [ 0.6015 -0.3717 -0.3717  0.6015]
 [-0.3717  0.6015 -0.6015  0.3717]]

1,3-ブタジエンには四つの分子軌道があってそのエネルギーは$E=\alpha - 1.618\beta$、$\alpha - 0.618\beta$、$\alpha + 0.618\beta$、$\alpha + 1.618\beta$です。$\beta$は負の値なので$\alpha + 1.618\beta$が一番安定です。$f_i = [2, 2, 0, 0]$で全ての$\pi$電子が結合性軌道に入っています。一番安定な分子軌道$\psi_1$の$c_{p1}$は次のようになります。$[c_{11}, c_{21}, c_{31}, c_{41}] = [0.3717, 0.6015, 0.6015, 0.3717]$。

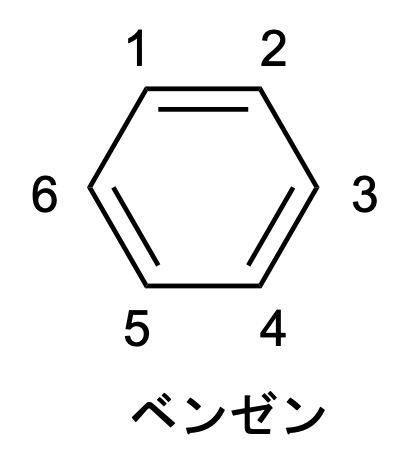
例２）ベンゼン

import numpy as np
H = huckel_hamiltonian(6, [(1,2), (2,3), (3,4), (4,5), (5,6), (6,1)])

ee, cc = np.linalg.eigh(H)
print(ee)
print(cc.round(4))

出力結果は以下になります。

[[0. 1. 0. 0. 0. 1.]
 [1. 0. 1. 0. 0. 0.]
 [0. 1. 0. 1. 0. 0.]
 [0. 0. 1. 0. 1. 0.]
 [0. 0. 0. 1. 0. 1.]
 [1. 0. 0. 0. 1. 0.]]
[-2. -1. -1.  1.  1.  2.]
[[ 0.4082  0.5774  0.      0.5774  0.      0.4082]
 [-0.4082 -0.2887 -0.5     0.2887 -0.5     0.4082]
 [ 0.4082 -0.2887  0.5    -0.2887 -0.5     0.4082]
 [-0.4082  0.5774  0.     -0.5774  0.      0.4082]
 [ 0.4082 -0.2887 -0.5    -0.2887  0.5     0.4082]
 [-0.4082 -0.2887  0.5     0.2887  0.5     0.4082]]

フロンティア軌道理論

最後に、Hückel法による計算でナフタレンの反応の位置選択性を予測してみましょう。

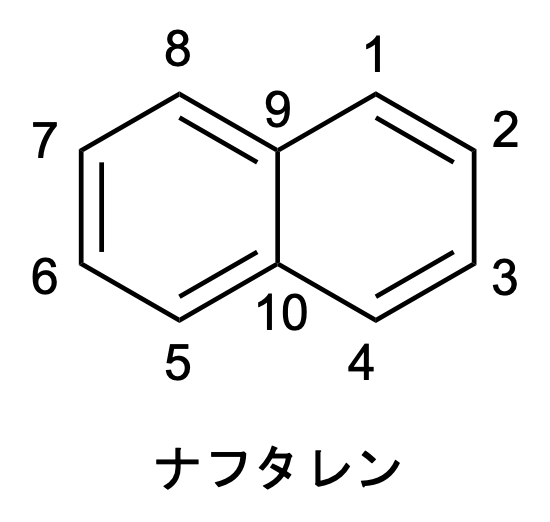
ナフタレンでは、図の1位の炭素に選択的に求電子置換反応が進行します。求電子置換反応は、ナフタレンから求電子剤へと電子が攻撃する反応です。この時、攻撃する電子は、電子が占有している分子軌道のうち最もエネルギーが高い軌道、すなわち最高被占位軌道(highest occupied molecular orbital, HOMO)の電子であり、HOMOの電子密度の最も高い位置で反応が起こります。ナフタレンは各炭素原子から一つずつ$\pi$電子が出され、10個の$\pi$電子を持ちます。したがって、基底状態のHOMOはエネルギーが5番目に低い分子軌道$\psi_5$です。また、$\psi_5$のp番目の原子軌道$\chi_p$の電子密度は$|c_{p5}|^2$をみれば良いです。

それでは、計算してみましょう。

H = huckel_hamiltonian(10, 
                       [(1,2),
                        (1,9),
                        (2,3),
                        (3,4),
                        (4,10),
                        (5,6),
                        (5,10),
                        (6,7),
                        (7,8),
                        (8,9),
                        (9,10),
                        ])

ee, cc = np.linalg.eigh(H)
print(ee.round(4))
print(cc.round(4))

出力結果は以下になります。

[[0. 1. 0. 0. 0. 0. 0. 0. 1. 0.]
 [1. 0. 1. 0. 0. 0. 0. 0. 0. 0.]
 [0. 1. 0. 1. 0. 0. 0. 0. 0. 0.]
 [0. 0. 1. 0. 0. 0. 0. 0. 0. 1.]
 [0. 0. 0. 0. 0. 1. 0. 0. 0. 1.]
 [0. 0. 0. 0. 1. 0. 1. 0. 0. 0.]
 [0. 0. 0. 0. 0. 1. 0. 1. 0. 0.]
 [0. 0. 0. 0. 0. 0. 1. 0. 1. 0.]
 [1. 0. 0. 0. 0. 0. 0. 1. 0. 1.]
 [0. 0. 0. 1. 1. 0. 0. 0. 1. 0.]]
[-2.3028 -1.618  -1.3028 -1.     -0.618   0.618   1.      1.3028  1.618  2.3028]
[[-0.3006 -0.2629  0.3996 -0.      0.4253  0.4253  0.      0.3996  0.2629  -0.3006]
 [ 0.2307  0.4253 -0.1735 -0.4082 -0.2629  0.2629  0.4082  0.1735  0.4253  -0.2307]
 [-0.2307 -0.4253 -0.1735  0.4082 -0.2629 -0.2629  0.4082 -0.1735  0.4253  -0.2307]
 [ 0.3006  0.2629  0.3996 -0.      0.4253 -0.4253 -0.     -0.3996  0.2629  -0.3006]
 [ 0.3006 -0.2629  0.3996  0.     -0.4253  0.4253 -0.     -0.3996 -0.2629  -0.3006]
 [-0.2307  0.4253 -0.1735  0.4082  0.2629  0.2629  0.4082 -0.1735 -0.4253  -0.2307]
 [ 0.2307 -0.4253 -0.1735 -0.4082  0.2629 -0.2629  0.4082  0.1735 -0.4253  -0.2307]
 [-0.3006  0.2629  0.3996 -0.     -0.4253 -0.4253  0.      0.3996 -0.2629  -0.3006]
 [ 0.4614 -0.     -0.347   0.4082  0.     -0.     -0.4082  0.347   0.  -0.4614]
 [-0.4614 -0.     -0.347  -0.4082 -0.      0.     -0.4082 -0.347   0.  -0.4614]]

$\psi_5$のp番目の原子軌道$\chi_p$の電子密度は$c_{p5}$を書き出します。
$[c_{15}, c_{25}, c_{35}, c_{45}, c_{55}, c_{65}, c_{75}, c_{85}, c_{95}, c_{105}] = [0.4253, 0.2629, -0.2629, -0.4253, 0.4253, 0.2629, -0.2629, -0.4253, 0, 0]$となりました。電子密度は$|c_{p5}|^2$なので、1位、4位、5位、8位の炭素の電子密度が大きいと求まりました。この４つの炭素は対称性から等価なので、これらの反応性が他の炭素より大きいことで、1位の炭素に選択的に求電子置換反応が進行するということがわかります。

HOMOに対して、電子が占有していない分子軌道のうち最もエネルギーが低い軌道を最低空軌道(Lowest Unoccupied Molecular Orbital、LUMO)と言います。HOMOとLUMOを合わせてフロンティア軌道と呼び、フロンティア軌道の電子が化学反応に関わるという考え方をフロンティア軌道理論と呼びます。実際には、有機反応には全電子の密度によって反応部位が決まるものと、フロンティア軌道の電子の密度によって反応部位が決まるものとがあって、ナフタレンの求電子置換反応は後者の反応でした

連載記事目次

・「Pythonによる化学シミュレーション入門」をやってみたよ~単分子一次反応の反応速度論~

・「Pythonによる化学シミュレーション入門」をやってみたよ2~色々な反応の反応速度~

・「Pythonによる化学シミュレーション入門」をやってみたよ3~振動反応~

・「Pythonによる化学シミュレーション入門」をやってみたよ4~ランダムウォークと拡散現象~

・「Pythonによる化学シミュレーション入門」をやってみたよ5~ブラウン運動とランジュバン方程式~

・「Pythonによる化学シミュレーション入門」をやってみたよ6~分子軌道法(1)~