この記事は現代化学(東京化学同人)の2022年4月号から2024年3月号まで連載された安藤耕司先生の「Pythonによる化学シミュレーション入門」を読んでやってみた記事です。詳しい内容は上記の「Pythonによる化学シミュレーション入門」をご参照ください。今回は、2023年10月号の分子軌道法(1)の内容です。
やること
Hückel法を用いて分子軌道のエネルギーを求めてみましょう
Hückel法の前提
Hückel法の導出はしません。Hückel法の前提知識についてまとめます。
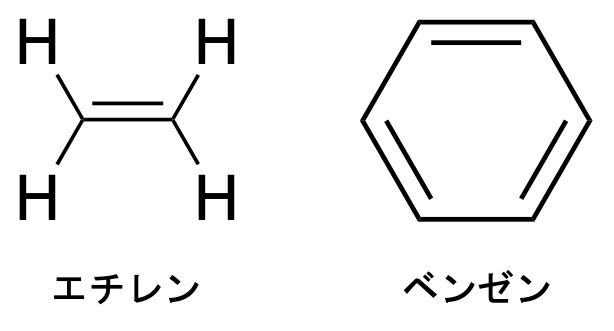
Hückel法とは、$\pi$電子のみを考慮した分子軌道法です。$\pi$電子というのは主に二重結合などに用いられる電子のことです。従って、Hückel法が対象とする分子は$\pi$結合を持つ化合物です。例えば、燃料として用いられるエチレン(C$_2$H$_4$)や、有機化学で有名なベンゼン(C$_6$H$_6$)などのエネルギーを計算できます。
Hückel法で求まるもの
以下の二つです。
(1)分子軌道のエネルギー
まず、分子が安定に存在できるかどうかなどがわかります。
量子化学計算からは、結合エネルギー、分子の生成熱、光吸収の有無などもわかります。
(2)分子軌道への各原子軌道の寄与
Hückel法では、分子軌道は、その分子を構成する各原子軌道の線型結合で表されるとします(LCAO近似)。式で表すと次のような感じです。
$$
\psi_i = \Sigma^N_p c_{pi} \chi_p
$$
ここで、$\psi_i$はi番目の分子軌道の波動関数、$\chi_p$はp番目の原子軌道の波動関数であり、この分子はN個の原子から構成されています。$c_{pi}$がp番目の分子軌道へのi番目の原子軌道の寄与であり、Hückel法ではこの$c_{pi}$を決定します。
結局のところ、Hückel法では何をしたいか
さまざまな近似を施したSchrödinger方程式を解きたいんです。先に、エチレンに対してHückel法を用いる場合に解くべき方程式を示してみます。
\left[
\begin{matrix} \alpha & \beta \\ \beta & \alpha \end{matrix}
\right]
\left[
\begin{matrix} c_1 \\ c_2 \end{matrix}
\right]
=
E
\left[
\begin{matrix} c_1 \\ c_2 \end{matrix}
\right]
LCAO近似を施す過程でSchrödinger方程式は行列になっています。教科書でよく見る流れとしては、手計算ではこのままだと大変なので永年方程式にして行列式を解きますが、pythonで解く場合は行列形式のハミルトニアンをそのまま入力して固有値と固有ベクトルを求めます。
Hückel法の計算手順
Hückel法は理論が難しいですが手順は簡単です。次の手順でできます。
(1)分子に対応した行列を作ります
(2)固有値問題を解きます
例)エチレン
まず、分子に対応した行列を作ります。行列は次のルールで作ります。
(1)$\pi$結合で繋がった原子の数nに対してn次正方行列を用意する
(2)対角要素を$\alpha$とする
(3)$\pi$結合している原子に番号をふり、i番目の原子とj番目の原子が隣接していれば、行列のij要素を$\beta$とする
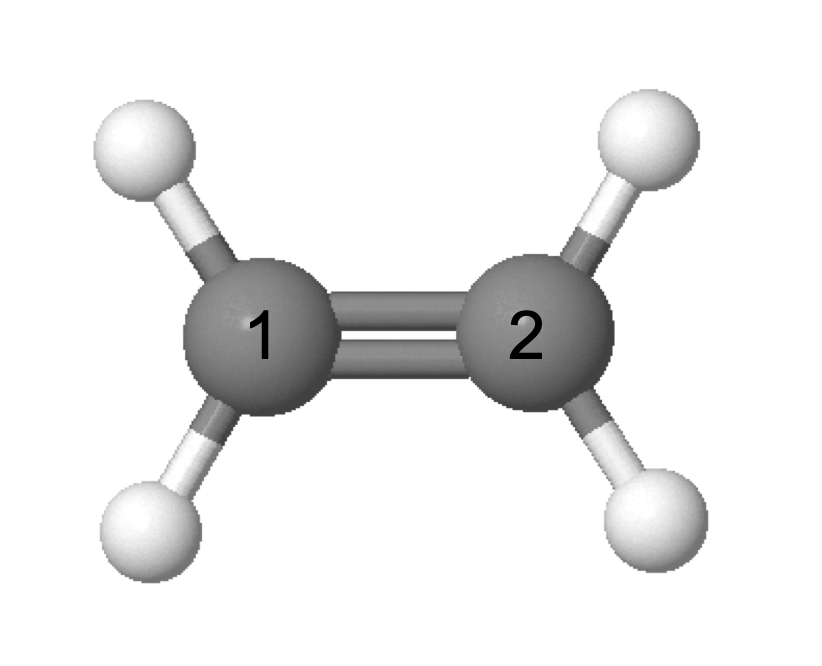
エチレンは二つの炭素原子が二重結合をしているので、二次正方行列を考えます。対角要素は$\alpha$であり、図のように番号をつけると、1番と2番の原子が隣接しているので行列の12要素と21要素を$\beta$にします。
\left[
\begin{matrix} \alpha & \beta \\ \beta & \alpha \end{matrix}
\right]
これをpythonで解きます。以下二通りの方法で解きます。
解き方1) sympyを使って
from sympy.abc import a, b
from sympy import Matrix, pprint
H = Matrix([
[a, b],
[b, a]
])
R, D = H.diagonalize()
pprint(D)
pprint(R)
出力
⎡a - b 0 ⎤
⎢ ⎥
⎣ 0 a + b⎦
⎡-1 1⎤
⎢ ⎥
⎣1 1⎦
対角行列$D$の要素が固有値で、$R$は固有ベクトルを並べたものです。
つまり$H$の固有値が$\alpha-\beta$と$\alpha+\beta$であり、それぞれの固有ベクトルが、
\left(
\begin{matrix} -1 \\ 1 \end{matrix}
\right)
,
\left(
\begin{matrix} 1 \\ 1 \end{matrix}
\right)
です。あらためて書き直すと、
\begin{cases}
E_1 = \alpha + \beta, \psi_1 = \frac{1}{\sqrt{2}}(\chi_1 + \chi_2)\\
E_2 = \alpha - \beta, \psi_2 = \frac{1}{\sqrt{2}}(\chi_1 - \chi_2)
\end{cases}
ここで、定義から$\beta$は負なので、よりエネルギーが低い軌道は$\psi_1$であり、規格化条件$c_1^2+c_2^2=1$を満たすために$\frac{1}{\sqrt{2}}$をつけています。
解き方2) numpyを使って
import numpy as np
a, b = 0, 1
H = np.array([
[a, b],
[b, a]
])
ee, cc = np.linalg.eigh(H)
print(ee)
print(cc.round(4))
出力
[-1. 1.]
[[-0.7071 0.7071]
[ 0.7071 0.7071]]
eeは固有値のリストです。この計算ではエネルギーの$\alpha$を原点にとって、その差分を計算しているので$-1$と$1$は$\alpha-\beta$と$\alpha+\beta$に対応します。ccは規格化条件を満たした縦ベクトルの固有ベクトルを並べています。
連載記事目次
・「Pythonによる化学シミュレーション入門」をやってみたよ~単分子一次反応の反応速度論~
・「Pythonによる化学シミュレーション入門」をやってみたよ2~色々な反応の反応速度~
・「Pythonによる化学シミュレーション入門」をやってみたよ3~振動反応~