勾配降下法をPythonで実装してみよう
前回までは勾配降下法を VBA で実装しましたが、今回は Python で実装してみます。
ただし、基本的には VBA のコードを書き換えたもので、行列演算などは使用しません。
「勾配降下法をVBAで実装してみる(一次式の場合)」のVBAのコードを単純に Python で書き換えたものです。
- 勾配降下法を、いま一つ腹落ちしていない過去の自分にくどくどと説明してみる。
- 勾配降下法(入力値が複数の場合の更新式)
- 勾配降下法をVBAで実装してみる(一次式の場合)
- 勾配降下法をVBAで実装してみる(二次式の場合)
データ
データは同じものを使います。
| No | x | y |
|---|---|---|
| 1 | 1.16 | 1.49 |
| 2 | 2.43 | 1.55 |
| 3 | 3.02 | 1.98 |
| 4 | 4.83 | 2.07 |
| 5 | 5.01 | 2.27 |
| 6 | 6.16 | 2.62 |
| 7 | 7.09 | 2.78 |
| 8 | 8.25 | 3.25 |
| 9 | 9.71 | 3.48 |
| 10 | 10.92 | 3.65 |
コード
こんな感じ。
import random
import numpy as np
import matplotlib.pyplot as plt
# [1] y = ax + b
def my_function(w0, w1, x):
return w0 + w1 * x
# [2] 学習率、パラメータの初期設定
LR = 0.001
ERR_POINT = 0.1
init_w0 = random.random()
init_w1 = random.random()
w0 = init_w0
w1 = init_w1
# [3] データの設定
x_data = [1.16, 2.43, 3.02, 4.83, 5.01, 6.16, 7.09, 8.25, 9.71, 10.92]
y_data = [1.49, 1.55, 1.98, 2.07, 2.27, 2.62, 2.78, 3.25, 3.48, 3.65]
count = 0
# [4] 学習
while count < 1000:
E = 0
grad_w0 = 0
grad_w1 = 0
#[5] データから誤差関数の値と各パラメータの勾配を求める
for x, y in zip(x_data, y_data):
y_ = my_function(w0, w1, x)
E = E + ((y - y_)**2)
grad_w0 += ((y_ - y) * 1)
grad_w1 += ((y_ - y) * x)
E = E * 0.5
#[6] 誤差が ERR_POINT 未満になったら学習を終了
if E < ERR_POINT:
break
#[7] パラメータを更新する
w0 -= (LR * grad_w0)
w1 -= (LR * grad_w1)
#[8] 途中経過を表示
#if count % 50:
# print('count:{0} / w0:{1:.3f} / w1:{2:.3f}'.format(count, w0, w1))
count += 1
# [9] 学習済みパラメータの表示
print('count:{0} / w0:{1:.3f} / w1:{2:.3f}'.format(count, w0, w1))
# [10] グラフの表示
x_ = np.linspace(start=0, stop=12, num=10)
y_ = []
init_y_ = []
for x in x_:
init_y_.append (my_function(init_w0, init_w1, x))
y_.append (my_function(w0, w1, x))
plt.plot(x_data, y_data, 'o')
plt.plot(x_, y_)
plt.plot(x_,init_y_)
plt.show()
コードの解説
ま、VBAのコードの移植なのでサクッとみていきましょう。
[1] y = ax + b
直線の式です。今回はパラメータとして $a$, $b$ の代わりに、$w_1$, $w_0$ を使いました。
$\qquad y = w_0 + w_{1}x$
単に変数名が異なるだけです。
[2] 学習率、パラメータの初期設定
それぞれの初期値と意味は以下の通りです。
| 定数名/変数名 | 初期値 | 意味 |
|---|---|---|
| LR | 0.001 | 学習率 |
| ERR_POINT | 0.1 | 学習終了判定誤差 |
| init_w0 | ランダム | w0の初期値 |
| init_w1 | ランダム | w1の初期値 |
| w0 | init_w0 と同じ | w0(バイアス) |
| w1 | init_w1 と同じ | w1(傾き) |
[3] データの設定
入力データと出力データを準備します。
x_data, y_data というリストを用意して格納しています。
[4] 学習
ループを回して学習を進めます。ループ回数が(今回は)1000回を超えたら強制的にループを抜けるようにしています。
[5] データから誤差関数の値と各パラメータの勾配を求める
現在のパラメータでの出力値を求めて、それを元に誤差と勾配を求めています。
VBA版では、誤差と勾配の計算は別々のループで行っていましたが、Python版では簡略化のためまとめちゃいました。ただこの場合、勾配計算の最後の1回分が無駄になります([7]のパラメータ更新前に[6]で学習を終了するので)。
[6] 誤差が ERR_POINT 未満になったら学習を終了
誤差が設定した誤差よりも小さくなったら学習を終了します。
[7] パラメータを更新する
以下の式の実装です。
$\qquad w_0 := w_0 - \eta(\frac{\partial E}{\partial w_0})$
$\qquad w_1 := w_1 - \eta(\frac{\partial E}{\partial w_1})$
[8] 途中経過を表示
途中のパラメータを表示させる場合はコメントをはずしてください。
[9] 学習済みパラメータの表示
学習結果のパラメータを表示します。
[10] グラフの表示
最後にグラフを表示します。
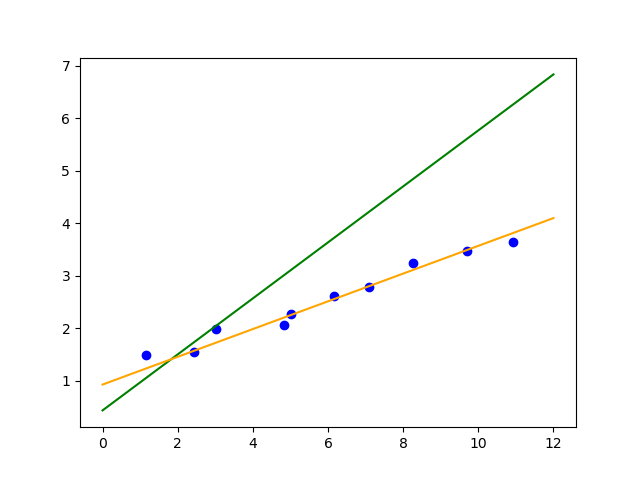
青い点はデータの散布図です。緑色の線は初期値のパラメータの線で、オレンジの線は学習済みのパラメータの線です。オレンジの線が青い点にフィットしているのがわかると思います。
(初期値はランダムで設定されるので、同じグラフになるわけではありません。)
まとめ
PythonでもVBAとほぼ同じコードで実装できました。
ロジックさえわかれば、あまり言語にこだわらなくても実装できると思うので、まずは自分の得意な言語で実装してみるのもいいかもしれませんね。
--Excel VBA でニューラルネットワークをフルスクラッチしてみる--
以前書いていたExcel VBAでニューラルネットワークをフルスクラッチしてみる的な記事は以下のブログに移動しました。
無限不可能性ドライブ