VBAで実装してみよう
前回、前々回 の記事で具体的なパラメータの更新方法はわかったけど、で?って感じですね。やっぱり実装して動きを確かめてみたいですよね。というわけで、今回は ExcelVBA で勾配降下法を実装してみようと思います。なんで Python とかじゃないのかっていうと、単に私が ExcelVBA の方が慣れているというのと、あと、シートに値を置いておいたり、同じシートにグラフを表示させたりと可視化が簡単だからです。私は GAS(Google Apps Script)は明るくないですが、たぶん移植はそれほど難しくないと思います(含み(w))。まぁ、実装だけを考えるなら、前回までの数式ベースの話はほとんどわからなくても大丈夫かな。要は、パラメータを更新する際にどういった式で更新すればいいかがわかればいいのです。
誤差関数とパラメータの更新式はわかっているので、これを実装すればいいですね。
誤算関数
$\qquad E = \frac{1}{2}\sum(y - \hat y)^2$
パラメータの更新式
$\qquad a := a - \eta(\frac{\partial E}{\partial a}) = a - \eta(\sum (\hat y_i - y_i) * x_i)$
$\qquad b := b - \eta(\frac{\partial E}{\partial b}) = b - \eta(\sum (\hat y_i - y_i) * 1)$
シートの準備
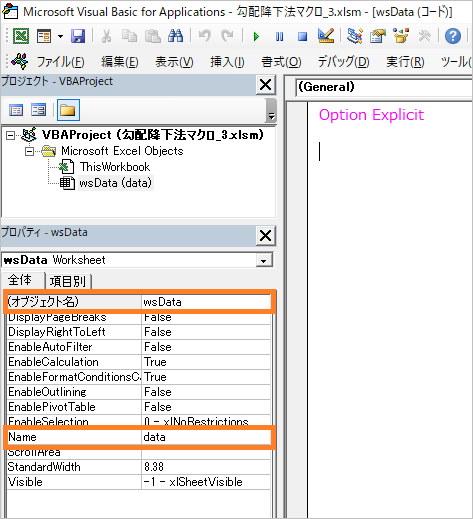
まずは、VBAでシートを扱いやすくするために、シートのオブジェクト名を変更しましょう。また、あわせてシート名も変えておきましょう。
| 対象 | 値(名前) |
|---|---|
| オブジェクト名 | wsData |
| Name | data |
シートにデータを入力する
今回は 入力 1 出力 1 のデータ 10 個を用意してみました。散布図を作るとわかりますが、各データには若干ランダム要素が入っています。「data」シートのB列に x(入力), C列に y(出力) のデータを入力します。(A列は単なる項番です。)
| No | x | y |
|---|---|---|
| 1 | 1.16 | 1.49 |
| 2 | 2.43 | 1.55 |
| 3 | 3.02 | 1.98 |
| 4 | 4.83 | 2.07 |
| 5 | 5.01 | 2.27 |
| 6 | 6.16 | 2.62 |
| 7 | 7.09 | 2.78 |
| 8 | 8.25 | 3.25 |
| 9 | 9.71 | 3.48 |
| 10 | 10.92 | 3.65 |
散布図を作成する
このデータをもとに散布図を作成します。B2~C11を選択して挿入-グラフから散布図を選択します。
グラフタイトルは不要なので削除してしまいましょう。また、軸の値を固定したいので、縦軸、横軸とも軸の書式設定で境界値の最小値、最大値を以下のように設定しておきます。(これを設定しないと、グラフを描画する際に、軸が動いてしまいます。)元から入っている値と同じにする場合は、一度別の値を入力してから、設定したい値を入力しなおすと左側の[自動]が[リセット]に変わって固定状態になります。
| 軸の設定値 | 最小値 | 最大値 |
|---|---|---|
| 横軸 | 0.0 | 12.0 |
| 縦軸 | 0.0 | 4.0 |
グラフはK列あたりに移動しておきましょう。
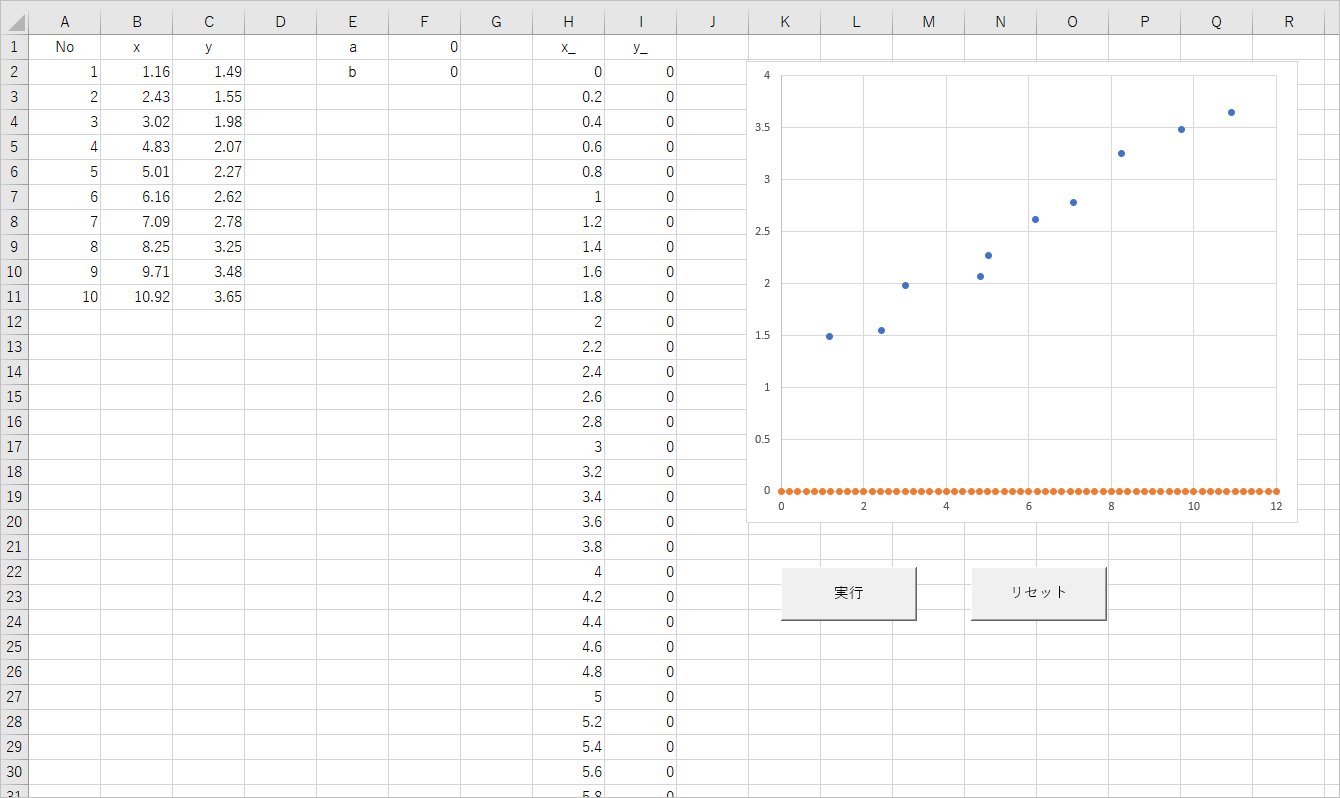
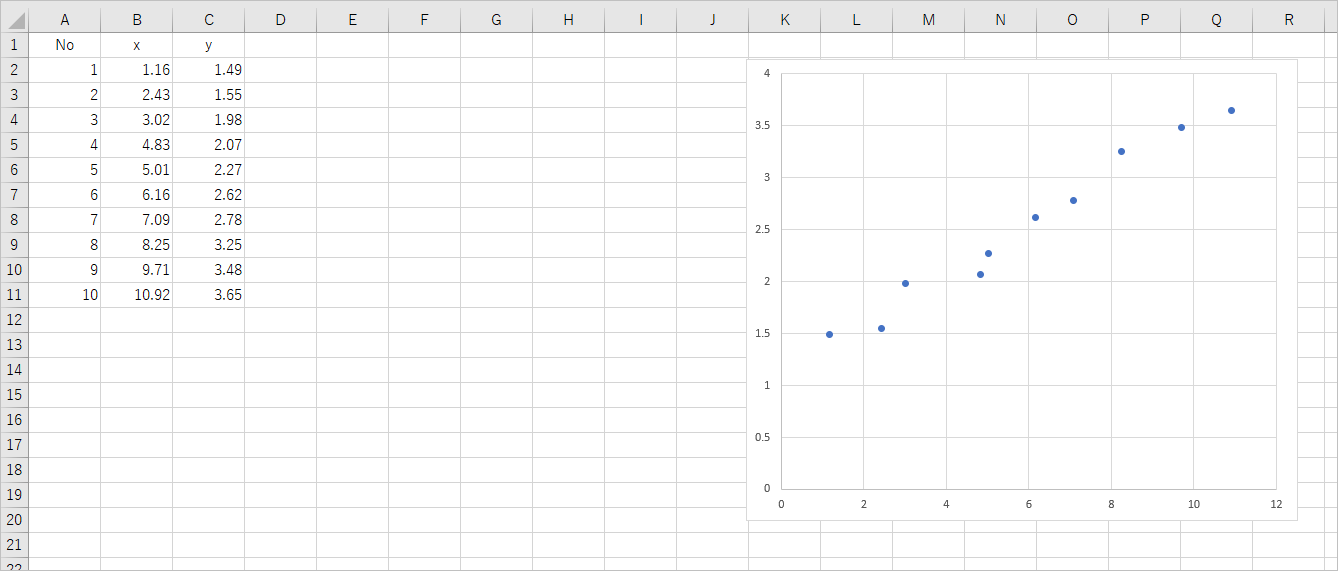
今のシートの状態はこんな感じです。
推測値のグラフを追加する
データを作成する
今回、勾配降下法でこのデータにフィットする直線の関数(パラメータ)を求めようとしています。パラメータの更新状況を視覚化したいので、そのグラフ(推測値のグラフ)を追加します。
パラメータ a, b を求めたいので、その値を格納するセルを用意します。
E1セル に a, E2セルに b と入力しておき、F1セルに a の値、F2セルに b の値を格納するようにします。
また、グラフ作成用の値を用意するため、H1セルに x_, I1セルに y_ と入力し、H2セルに 0 を入力しておきます。
今回は、入力 1 出力 1 で、関数としては $y = ax + b$ の形のものを求めようとしています。なので、y_ はパラメータ x_ に a を掛けて b を足すことで求めます。具体的には I2セル に「=$F$1*H2+$F$2」の計算式を入力します。各セルへの入力値を表にしておきます。
| セル | 値 |
|---|---|
| E1 | a |
| E2 | b |
| F1 | 0 |
| F2 | 0 |
| H1 | x_ |
| I1 | y_ |
| H2 | 0 |
| I2 | =$F$1*H2+$F$2 |
ここまで入力できたら、H2セルを選択して、ホーム - フィル - 連続データの作成で「範囲」を「列」、「種類」を「加算」、「増分値」を「0.2」、「停止値」を「12」にして連続データを作成します。
連続データが作成できたら、I2セルの数式を縦方向にコピー(オートフィル)します。
グラフを追加する
推測値用グラフのデータが作成できたので、これを先ほどのグラフに表示させましょう。
グラフを選択して「デザイン」タブの[ データの選択 ]をクリックし、「データソースのダイアログ」を表示させます。
左側の「凡例項目(系列)」の[ 追加 ]ボタンをクリックして、「系列の編集」ダイアログを表示させ、
系列名:ブランクのまま
系列 X の値:上矢印をクリックして H2:H62 を範囲指定(x_のデータ範囲)
系列 Y の値:上矢印をクリックして I2:I62 を範囲指定(y_のデータ範囲)
として、[ OK ]を(2回)押してダイアログを閉じます。
そうすると、グラフに新しい点線が追加されます。(オレンジの点線)
シート完成
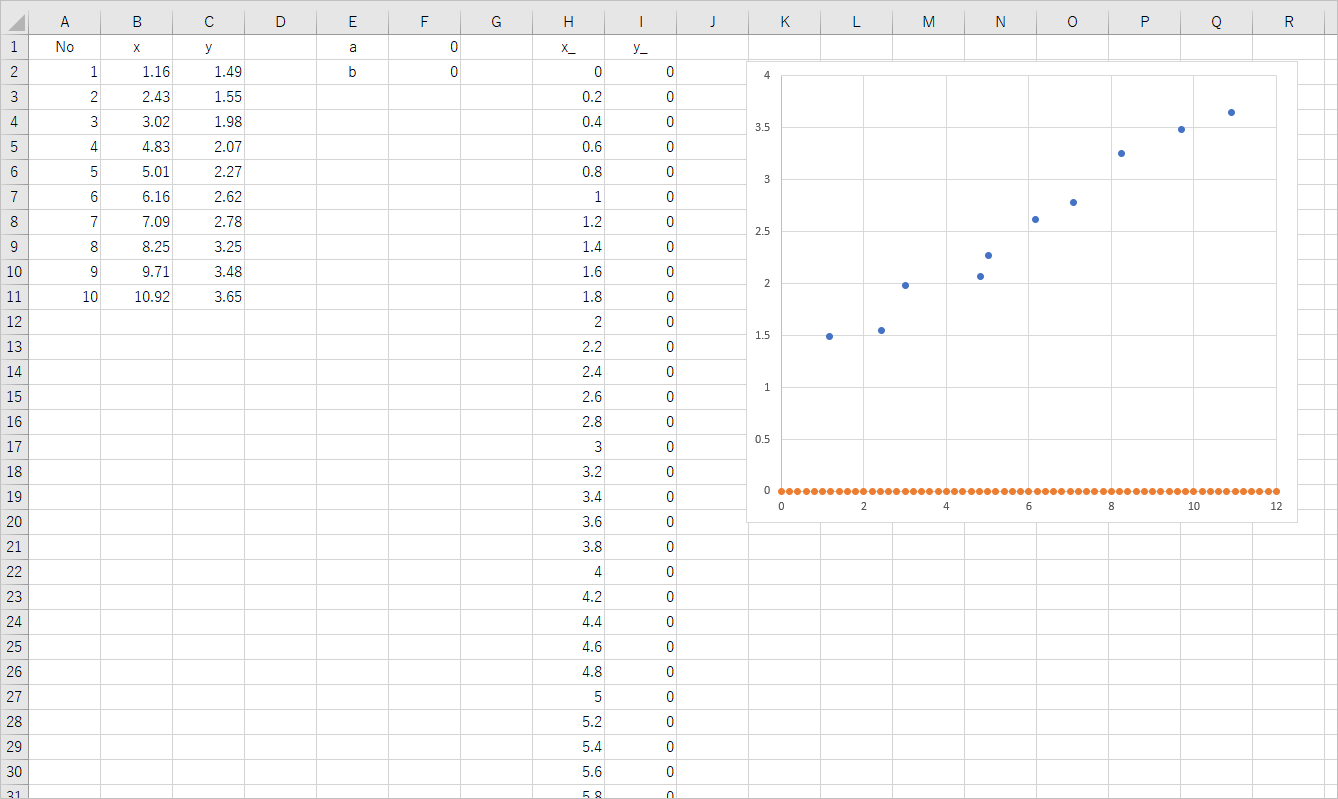
これでシートの準備が完了しました。このような感じになっていれば OK です。
実装
では、VBEを開いてコードを実装していきます。
はじめに標準モジュールを追加してください。コードはこの標準モジュールに書いていきます。
動作の確認が目的なので、拡張性や保守性についてはほとんど(まったく?)考慮していませんのでご了承ください。
関数式の部分の実装
今回、求める直線の式として y = ax + b を設定しています。まずはこの部分を実装してみましょう。
コードは単純で以下のようになります。(Function名は適宜イケてるものに直しちゃってください。)
'求める直線の式
Private Function myFunction(ByRef a As Double, ByRef x As Double, ByRef b As Double) As Double
'y = ax + b
myFunction = a * x + b
End Function
まぁ、そのままですね。
メイン部分の実装
コードについては下で解説します。
'[1]メインの処理
Public Sub Click_実行()
Dim a As Double 'パラメータ a(傾き)
Dim b As Double 'パラメータ b(切片)
Dim grad_a As Double 'パラメータ a に関する誤差関数の勾配
Dim grad_b As Double 'パラメータ b に関する誤差関数の勾配
Dim E As Double '誤差
Dim x As Double '入力値
Dim y As Double '(正しい)出力値、正解ラベル
Dim y_ As Double '推測値
Dim r As Long '行カウンタ
Dim cnt As Long '回数カウンタ
Const LR As Double = 0.001 '学習率
Const ERR_POINT As Double = 0.1 '学習終了判定誤差(0.1 は恣意的に決めた値)
Const MAX_LOOP_COUNT As Long = 1000 '最大ループカウント数
'[2]パラメータ a, b の初期値にランダムな値を設定する
Randomize
a = Rnd
b = Rnd
With wsData
'[3]パラメータを更新していい感じの値にするために処理を繰り返す
cnt = 0
Do
'------------------------------------------------
'[4]いまのパラメータでの誤差を求める(E:誤差)
E = 0
For r = 2 To 10
'[5]いまのパラメータでの推測値を求める
x = .Cells(r, 2).Value
y_ = myFunction(a, x, b)
'[6-1]誤差関数
y = .Cells(r, 3).Value
E = E + ((y - y_) ^ 2)
Next
'[6-2]誤差関数
E = E * 0.5
'------------------------------------------------
'[7]誤差が 学習終了判定誤差 未満ならループを抜ける
If E < ERR_POINT Then
Exit Do
End If
'------------------------------------------------
'[8]勾配を求めてパラメータ a, b を更新する
grad_b = 0
grad_a = 0
For r = 2 To 10
'[9]いまのパラメータでの推測値を求める([4]と同じ)
x = .Cells(r, 2).Value
y_ = myFunction(a, x, b)
'[10]a, b の勾配を求める(sum((推測値 - 正解値) * そのパラメータにかかる入力値 の式))
y = .Cells(r, 3).Value
grad_a = grad_a + ((y_ - y) * x)
grad_b = grad_b + ((y_ - y) * 1)
Next
'[11]勾配に学習率を掛けてパラメータ a, b を更新する
a = a - (LR * grad_a)
b = b - (LR * grad_b)
'------------------------------------------------
'[12]回数をカウントアップして、回数、誤差をステータスバーに表示
cnt = cnt + 1
Application.StatusBar = cnt & "回 / E = " & WorksheetFunction.Round(E, 2)
'[13]10回に1回グラフを更新
If cnt Mod 10 = 0 Then
DoEvents
DoEvents
.Range("F1").Value = a
.Range("F2").Value = b
End If
'[14]無限ループ回避のため、cnt > MAX_LOOP_COUNT で強制的にループを抜ける
Loop Until cnt >= MAX_LOOP_COUNT
'[15]求まったパラメータ a, b の値をセルに格納
.Range("F1").Value = a
.Range("F2").Value = b
End With
MsgBox "パラメータが求まりました。"
Application.StatusBar = False
End Sub
[1]メインの処理
ボタンで呼び出せるように Public なプロシージャにしておきます。プロシージャ名は「Click_実行()」としました。
また、必要な変数や定数を宣言しておきましょう。小数を扱うので変数の型は基本的には Double です。
[2]パラメータ a, b の初期値にランダムな値を設定する
パラメータ a, b の初期値はランダムで決定します。
[3]パラメータを更新していい感じの値にするために処理を繰り返す
ここが本体ですね。「勾配降下法を、いま一つ腹落ちしていない過去の自分にくどくどと説明してみる。」の記事で500回とか1500回とか繰り返し計算していた部分です。今回は誤差が一定値未満になったらループを抜けるようにしていますが、間違って無限ループにはまらないとも限らないので、1000回まででループを抜けるようにしています。
[4]いまのパラメータでの誤差を求める(E:誤差)
現時点のパラメータ a, b での誤差を求めています。For-Next で全データについて処理をしてそれぞれの誤差の総和をとっています。
[5]いまのパラメータでの推測値を求める
「myFunction」プロシージャを呼び出して、現時点のパラメータ a, b での推測値(出力値)を求めています。計算結果は推測値の変数「y_」に格納しています。y_ は数式での $\hat y$ を表しています。
[6-1][6-2]誤差関数
正解値(y)と推測値(y_)を元に誤差を求めています。
$\qquad E = \frac{1}{2}\sum(y - \hat y)^2$
の式の実装です。(コードでは最後に 0.5 を乗算することで $\frac{1}{2}$ としています。)
[7]誤差が 学習終了判定誤差 未満ならループを抜ける
誤差が学習終了判定誤差未満になったら学習が完了した(いい感じのパラメータが求まった)と判断して Do - Loop を抜けます。学習終了判定誤差の 0.1 という値は恣意的に決めた値です。ただし、あまり大きいとイケてない(パラメータの)状態でループを抜けてしまいますし、小さすぎるとなかなか学習が終了しなくなります。なお、「学習終了判定誤差」はここだけの言い回しです。
[8]勾配を求めてパラメータ a, b を更新する
パラメータ更新のキモです。以下の式の実装です。
$\qquad a := a - \eta(\frac{\partial E}{\partial a}) = a - \eta(\sum (\hat y_i - y_i) * x_i)$
$\qquad b := b - \eta(\frac{\partial E}{\partial b}) = b - \eta(\sum (\hat y_i - y_i) * 1)$
For - Next でデータ分繰り返して 勾配の総和を求めています。
[9]いまのパラメータでの推測値を求める([4]と同じ)
ここまでではパラメータはまだ更新されていないので、計算的には[4]の処理とまったく同じです。[4]で一度計算しているので、配列に格納しておいて使いまわすようにしてもよいかもしれません。
[10]a, b の勾配を求める
「勾配降下法を、いま一つ腹落ちしていない過去の自分にくどくどと説明してみる。」で偏微分ならなにやらでややこしい計算をした部分です。ですが、実際に使う式は以下の単純化された式です。
$\qquad \sum((推測値 - 正解値) * そのパラメータにかかる入力値$
「推測値」は[9]で求めて y_ に格納しています。「正解値」はシート(の3列目)の値です。「入力値」も[9]で x に格納しています。というわけで、単純に
$\qquad$ (y_ - y) * x
$\qquad$ (y_ - y) * 1
と計算できます。ただし、パラメータ b については、入力値は 1 としています。(わざわざ 1 を掛けなくてもいいのですが、他のパラメータの式と表記を合わせるため 1 を掛けています。)
この計算を For - Next で繰り返して、総和をとっています。
[11]勾配に学習率を掛けてパラメータ a, b を更新する
求めた勾配の総和に学習率を掛けてパラメータを更新しています。
$\qquad a:=a-\eta(\frac{\partial E}{\partial a})$
$\qquad b:=b-\eta(\frac{\partial E}{\partial b})$
[12]回数をカウントアップして、回数、誤差をステータスバーに表示
カウンタをカウントアップしてステータスバーに進捗を表示しています。
誤差を小数第二位まで表示させています。
[13]グラフを更新
F1セルに a の値、F2セルに b の値を格納し、グラフを更新します。
適当に 10 回に 1 回にしていますが、PCのスペックに合わせて調整してください。
DoEvents を 2 回書くことで、グラフが動いているように表現できます。
(PCによっては1回でも問題ないことがあります)
[14]無限ループ回避のため、cnt > MAX_LOOP_COUNT で強制的にループを抜ける
学習が収束しないと無限ループに陥ることがあります。それを避けるために最大ループカウント数を設定し、それを超えたらループを抜けるようにしています。学習率の設定値によっては、学習が進んでいてもいい感じのパラメータが求まる前に最大ループカウント数に到達してしまうこともあるので、状況に応じて値を変えるようにします。今回は1000回に設定しています。
[15]求まったパラメータ a, b の値をセルに格納
最後に a, b の値を F1セル、F2セルに格納して処理を終了します。
リセット処理
パラメータをリセットする処理です。
Public Sub Click_リセット()
With wsData
.Range("F1").Value = 0
.Range("F2").Value = 0
End With
End Sub
マクロの登録
シートに【実行】ボタンと【リセット】ボタンを作成し、それぞれにマクロを登録しましょう。
| ボタン | マクロ |
|---|---|
| 実行 | Click_実行 |
| リセット | Click_リセット |
最終的なシートの状態
実行してみましょう!
では【実行】ボタンを押して処理を実行してみましょう!
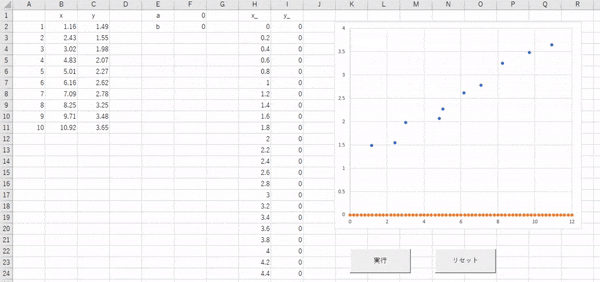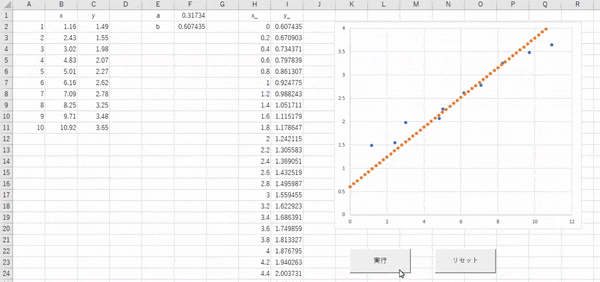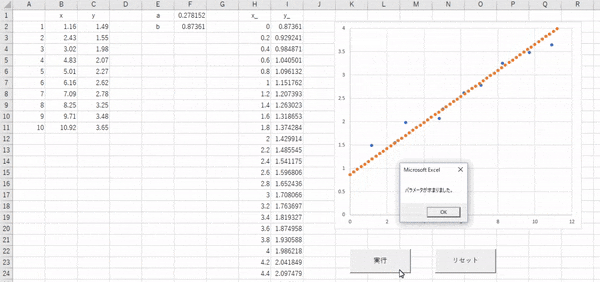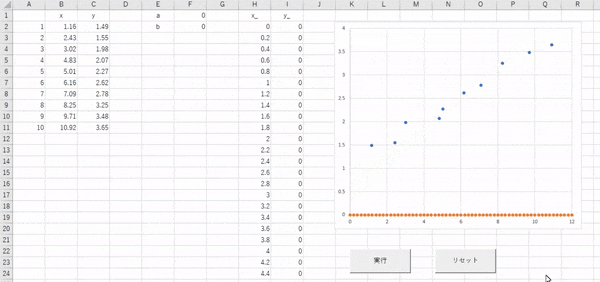
このようになればOKです。オレンジの点線が徐々にプロットした青い点にいい感じに重なるように移動していきますね。
別のデータで試してみる
さて、x とか y とかの味気ないデータではあまり面白くないので、最後にもうちょっと意味のありそう?なデータで動かしてみましょう。
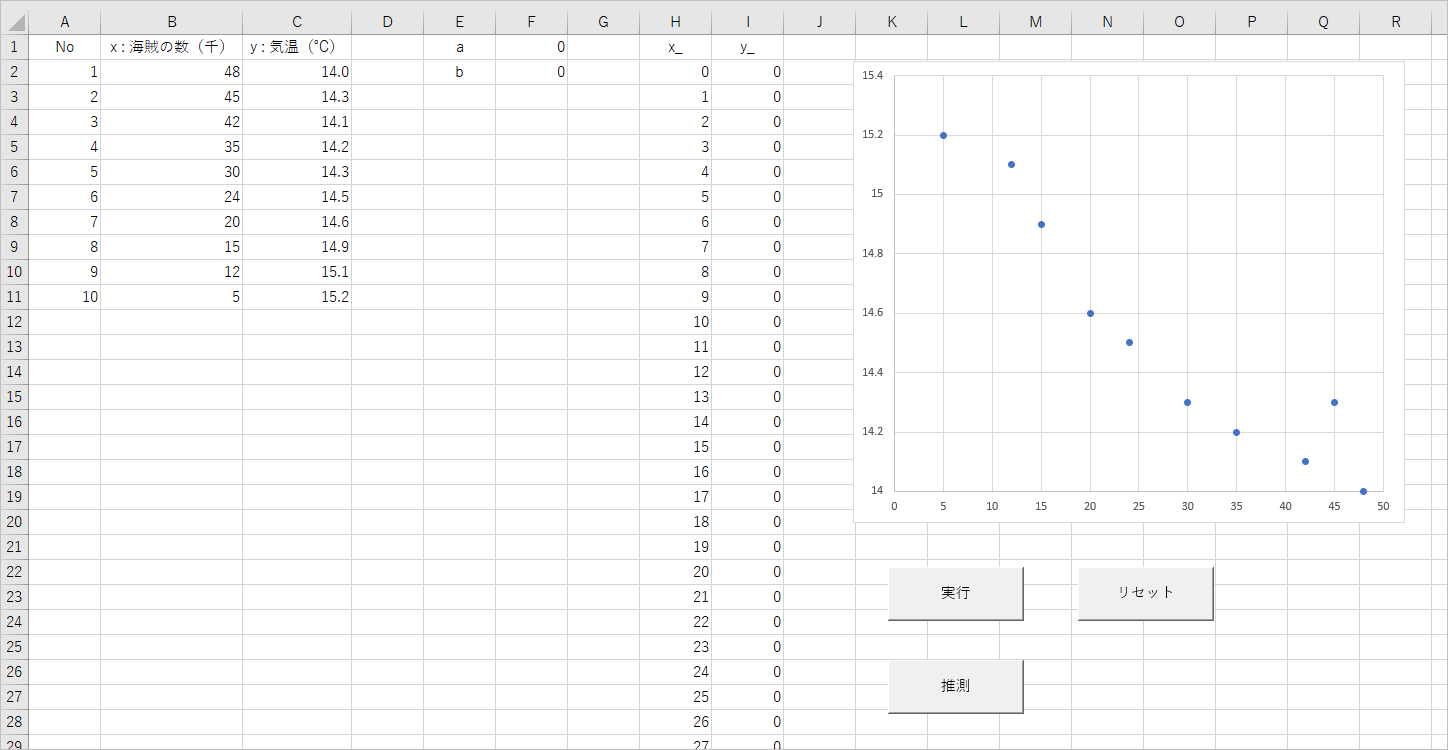
海賊と気温の関係
これは海賊と気温の関係を調べたデータです。よく言われているように海賊の数と地球の気温には負の相関関係があります。(データはここのウィキペディアにあったものを少し加工してあります。)
いつも右上がりのデータではつまらないので、今回は左上がりのデータにしてみました。
| No | x : 海賊(千) | y : 気温(℃) |
|---|---|---|
| 1 | 48 | 14.0 |
| 2 | 45 | 14.3 |
| 3 | 42 | 14.1 |
| 4 | 35 | 14.2 |
| 5 | 30 | 14.3 |
| 6 | 24 | 14.5 |
| 7 | 20 | 14.6 |
| 8 | 15 | 14.9 |
| 9 | 12 | 15.1 |
| 10 | 5 | 15.2 |
グラフの準備
H列にグラフ用のデータを用意します。0 から 1 刻みで 50 までにすればいいでしょう。
また、グラフの縦軸、横軸の最大値、最小値を設定します。
| 軸の設定値 | 最小値 | 最大値 |
|---|---|---|
| 横軸 | 0.0 | 50.0 |
| 縦軸 | 14.0 | 15.4 |
コードの変更
コードを変更します。といっても定数の値を変えるだけです。次のように設定しましょう。ちなみに、学習率はこれより大きいと収束しないようです。また、データがアレなので、学習終了判定誤差もこれ以上は小さくなりづらそうです。
| 定数 | 値 | 意味 |
|---|---|---|
| LR | 0.0002 | 学習率 |
| ERR_POINT | 0.08 | 学習終了判定誤差 |
| MAX_LOOP_COUNT | 30000 | 最大ループカウント数 |
実行してみましょう!
準備ができたら実行してみましょう。だいたい 22000 回くらいで学習が終了すると思います。
推測機能を追加しよう
せっかくなので求まったパラメータを元に値を推測させてみましょう。
以下のコードを入力し、【推測】ボタンを作って登録してみます。
Public Sub Click_推測()
Dim a As Double
Dim b As Double
Dim x As Double
Dim y_ As Double
With wsData
a = .Range("F1").Value
b = .Range("F2").Value
x = CDbl(InputBox("海賊の数(x)はどのくらいですか?"))
y_ = myFunction(a, x, b)
MsgBox "地球の気温は " & Format(y_, "0.0") & " ℃くらいです。"
End With
End Sub
できたら【推測】ボタンをクリックし、海賊の数を入力して地球の気温を推測してみましょう。
まとめ
パラメータの更新式を求めるまでの数式はごちゃごちゃ面倒な感じでしたが、実装だけを考えると単純化された式だけを利用すればよいということがわかりました。また、学習率を変えるといろいろと挙動が変わるので試してみると良いかと思います。
今回のコードではデータを一つ一つ処理しているので動作速度はあまり速くありませんが、実際には行列計算を用いて一気に計算してしまいます。Python では NumPy を使って行列計算できるので、効率的に計算できますね。その代わり今回のような VBA での実装では、ひとつひとつ具体的に何をしているのかがわかりやすいのではないでしょうか。
--Excel VBA でニューラルネットワークをフルスクラッチしてみる--
以前書いていたExcel VBAでニューラルネットワークをフルスクラッチしてみる的な記事は以下のブログに移動しました。
無限不可能性ドライブ