この記事の目的
ExcelVBAで確率的勾配降下法を実装したり、ニューラルネットワークをフルスクラッチしたり、順伝播の式を偏微分して逆伝播の更新式を求めたりっていうのはなんとなくできるようになったかなという感じですが、一番のキモになる(と思っている)「勾配降下法」がいま一つ腹落ちしない状態が1年以上続いていて、ここがわからないと「ひとに説明できないじゃないですか。やだー」な状態から脱出できないので、なんとかこれなら過去の自分でも理解できるかも…という説明をこの記事ではしていこうと思います。
勾配降下法の理屈(考え方)自体はそれほど難しくないとは思いますが、まぁ、正しい出力値($y$)と予測値($\hat{y}$)との誤差を求めて、この誤差を最小にするパラメータを求めれば正しい出力(に限りなく近い)値が計算できる関数を得られるというアプローチなので、まぁ、そうだよね。という感じですね。
で、この誤差を最小にするために、誤差関数(損失関数、目的関数)というものを設定して最小となるところを求めればいい感じのパラメータが得られますね。というのもまぁ、そうかもね。
で、誤差関数の最小となるところを求めるには微分して(接線の)傾きがゼロになる値を求めればいいよね。というのもよくある最小化問題だから微分だよね。というアプローチなので、うん、まぁ、そうですよね。
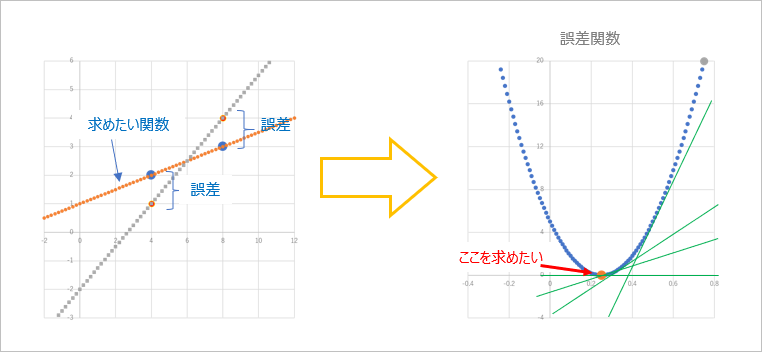
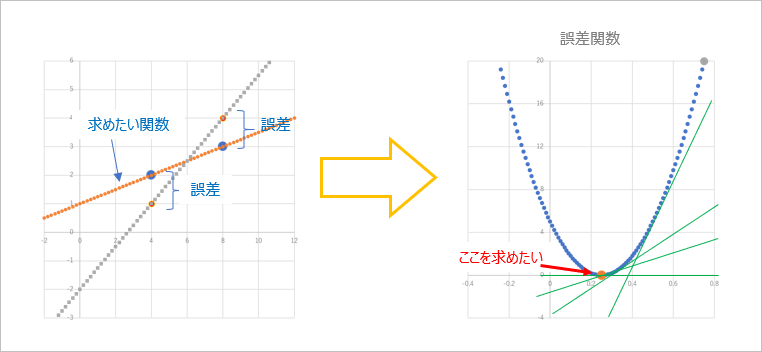
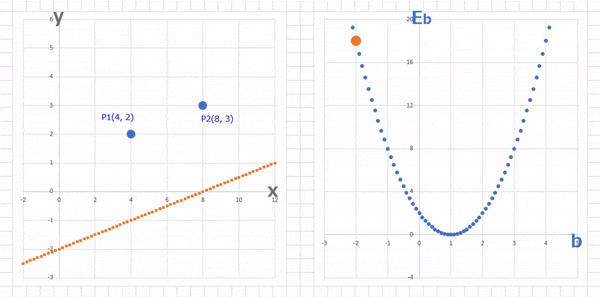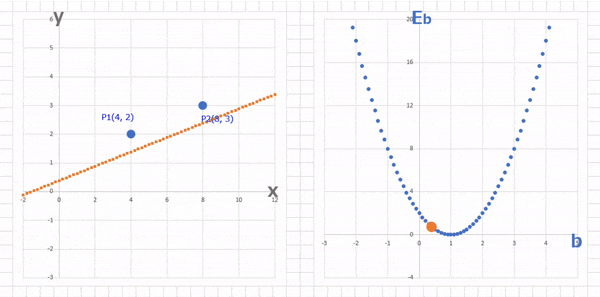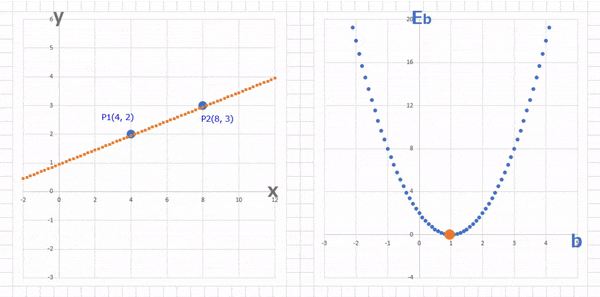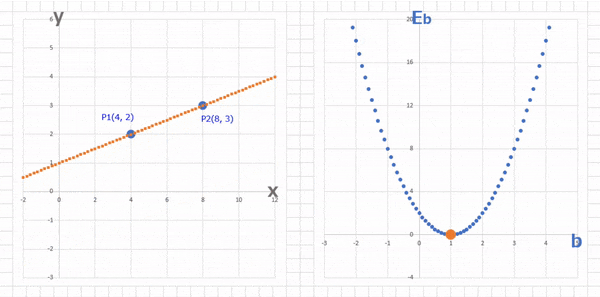
で、ここでよく出てくる図がこんな感じ。
とまぁ、順序立てて説明されると「うん…まぁ、そうかも。。」という気にはなるのですが、じゃあなんで誤差関数の最小値を求めるといい感じのパラメータが求まるの?そもそも例えば直線 $y = ax + b$ で入力を $x$,出力を $y$ とすると、求めなきゃいけないパラメータって $a$, $b$ (あるいは $y = wx + b$ として 重み($w$)とバイアス($b$)でもいいのですが)の2つあるけど、誤差関数の最小値ってこの $a$, $b$ (あるいは $w$, $b$)とどう関係してるの?っていうか、どっち?というのがなんだかよくわからない…なにか致命的な勘違いしてる? $y = ax + b$ の $a$, $b$ を求めようとしていて、誤差関数を二乗誤差関数とするとよくあるのが例えば $y = x^2$ のグラフが出てきて、これを $x$ で微分してゼロになる値を求めると $2x = 0$ だから $x = 0$ だよね。というようなもの。このグラフの最小となる点は $x = 0$ なので、これを求められれば解決です。…ですよね。で、ここからわからなくなるのですが、このいま求まった $x = 0$ ってなに?僕らはたしか $a$ とか $b$ とか $w$ とか $b$ とかのパラメータの(限りなく正しい)値を求めたかったんだけど… $x = 0$ やったね! …で?…という感じ。たぶんこれは 直線 $y = ax + b$ から誤差関数 $y = x^2$ に話が移る際に、変数がすり替わってる?からわかりにくくなってるのかな?誤差関数の $y$ とか $x$ って、そもそも設定していた入力 $x$, 出力 $y$ とは別のものなんですよね。たぶん、ほかの人たちは「そんなのあたりまえですよね」なのかもしれないのですが、私はここにハマってなかなか脱出できなかったわけです。この左側のグラフと右側のグラフ、それぞれの意味はわかるけどつながりがよくわからない。
で、まぁ、そんな勘違いというかなんだかやっぱりよくわからない状態が続いていた過去の自分に「それってこういうことじゃない?」というのをこの記事ではくどくどと説明していこうと思います。すごく冗長に。
問題設定
まずは問題設定。
$x = 4$ のときの出力 $y$ が $2$, $x = 8$ のときの出力 $y$ が $3$ になるような関数 ($f(x)$, $y = ax + b$)を求めたい。
こんな少ないデータで大丈夫か?大丈夫だ、問題ない。というか、ここで無駄にデータを多くしても無駄に計算が面倒になるだけなので、とっかかりとしてはこのくらいでいいんじゃないかと思います。いいですよね。
表にするとこんな感じ。
| x | y | |
|---|---|---|
| データ 1 | 4 | 2 |
| データ 2 | 8 | 3 |
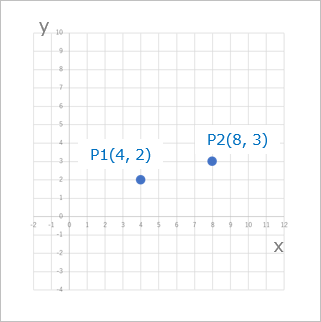
ひとつの入力データ($x$)に対して出力($y$)がひとつなので、図にするとこんな感じ。

いまこの2つの入出力を座標で表すと、点$P_1$として($x_1$, $y_1$), 点$P_2$として($x_2$, $y_2$)とすると、$P_1$($4$, $2$), $P_2$($8$, $3$)となるわけで、これをプロットするとこうなります。
この2点$P_1$, $P_2$ を通る直線でもっとも誤差が少ない直線は、当然この2点上を通る直線で、これは解析的に $y = 0.25x + 1$ と求められるわけです。
どう求めるかというと、$x$ と $y$ の共分散を $x$ の分散で割ったものが $a$, $a$ に $x$ の平均を掛けたものを $y$ の平均から引いたものが $b$ になります。
具体的には、
xの平均
$\qquad \mu_x = (4 + 8) / 2 = 6$
yの平均
$\qquad \mu_y = (2 + 3) / 2 = 2.5$
xとyの共分散
$\qquad \frac{1}{n} \sum_{i=1}^{n}(x_i - \mu_x)(y_i - \mu_y) = \frac{1}{2}((4-6)(2-2.5)+(8-6)(3-2.5)) = 1$
xの分散
$\qquad \frac{1}{n} \sum_{i=1}^{n}(x_i - \mu_x)^2 = \frac{1}{2}((4-6)^2+(8-6)^2) = 4$
なので、
$\qquad a = (xとyの共分散)/(xの分散) = 1/4 = 0.25$
$\qquad b = \mu_y - (a * \mu_x) = 2.5 - (0.25 * 6) = 1$
よって、
$\qquad y = 0.25x + 1$
で、実際この直線を引いてみると…
ばっちり $P_1$, $P_2$ にフィットしてますね。
実際この関数に $x_1$, $x_2$ の値を代入して計算してみると、
(1-1)$\qquad x_1: 0.25 * 4 + 1 = 2(= y_1)$
(1-2)$\qquad x_2: 0.25 * 8 + 1 = 3(= y_2)$
となるのでちゃんと期待通りの結果になりました。
パチパチパチ。
で、勾配降下法ではこの解析的に求めた関数をなんとかごにょごにょやって求めるというチャレンジをします。
何を求めるかというと、$y = ax + b$ の $a$ と $b$ いわゆる 傾きと切片 です。
機械学習風に書くと、 $y = wx + b$ とか $y = w_0 + w_1x$ とかでしょうか。
$a$ の部分が重み($w$ もしくは $w_1$)、$b$の部分がバイアス($b$ もしくは $w_0$)に該当します。
そうそう、この「何を求めようとしているのか」というのを常に意識しておくと良いと思います。
というのは、中学とか高校の数学の場合、たいていは 「$x$(や $y$) の値を求める」問題だと思うので、ついつい $x$ とか $y$ に意識が向いちゃいますが、今回求めたいのは $a$ とか $b$ の方なのです。
まずは適当に
さて、たいていのヒトならさっきのプロットされた図を見ればこの2点にフィットする直線は直感的に引けちゃいます。わざわざ計算しなくてもさっと引けちゃいます。なんか共分散とか分散とかよくわからんものを持ち出さなくても、なんなら小学生でも引けちゃいます。引けますよね?
ただ、コンピュータにはそんな芸当はできないので、じゃあ、どうするかというと、まずは適当にパラメータを決めて線を引きます。
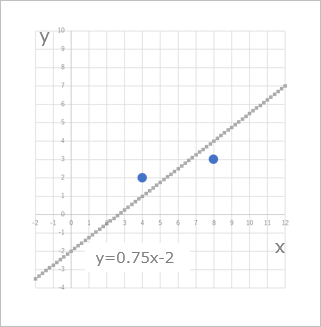
いま、パラメータを適当に $a = 0.75$, $b = -2$ にしたとします。適当にです。
この直線を引いてみましょう。
このようになりました。
計算してみると、
(1-3)$\qquad x_1: 0.75 * 4 - 2 = 1(= \hat{y_1})$
(1-4)$\qquad x_2: 0.75 * 8 - 2 = 4(= \hat{y_2})$
となって、求めたい$y_1$, $y_2$ とは違う値になってしまっています。
このいま適当に決めたパラメータをどうにか調整して、正しいパラメータに近づけていきます。
誤差を求める
パラメータを調整するにはいま適当に決めたパラメータでの出力、これを予測値として $\hat{y}$ で表すとすると、この $\hat{y}$ と正しい出力の $y$ とがどれだけ異なっているかを調べればよさそうです。このどれだけ異なっているかを誤差といって、この誤差を調整して誤差がゼロになれば(誤差がなくなれば)、まぁ、正しい値になるよね。という発想です。
誤差をゼロにするにはそれぞれの点での誤差をゼロにできればよく、それはつまり、それぞれの点の誤差の合計がゼロになればいいよねというのと同じですね。ここで、$x_1$ での誤差を $E_1$、$x_2$ での誤差を $E_2$、誤差の合計を $E$ とすると、
$\qquad E_1 = y_1 - \hat{y_1} = 2 - 1 = 1$
$\qquad E_2 = y_2 - \hat{y_2} = 3 - 4 = -1$
$\qquad E = E_1 + E_2 = 1 + (-1) = 0$
となってしまって、誤差の合計はゼロだけど、でもこの $a = 0.75$, $b = -2$ って求めたいパラメータじゃないですよね。となってしまいます。
で、これを回避するために、それぞれの誤差を2乗することにします。2乗すればマイナスでもプラスになるので、互いに相殺することがなくなりますね。
(1-5)$\qquad E_1 = (y_1 - \hat{y_1})^2 = (2 - 1)^2 = 1^2 = 1$
(1-6)$\qquad E_2 = (y_2 - \hat{y_2})^2 = (3 - 4)^2 = (-1)^2 = 1$
(1-7)$\qquad E = 1 + 1 = 2$
となって、ちゃんと(?)誤差が $2$ と算出されました。
誤差を求める関数を設定する
さて、いま誤差の合計を求めた式を一般化してみましょう。$E_1$ は $(y_1 - \hat{y_1})^2$, $E_2$ は $(y_2 - \hat{y_2})^2$ と計算しています。で、いま、パラメータは適当に決めちゃっていて、それぞれ $a = 0.75$, $b = -2$ という値になっているので、
$\qquad\hat{y_1} = ax_1 + b = 0.75x_1 - 2$
$\qquad\hat{y_2} = ax_2 + b = 0.75x_2 - 2$
という計算式になっています。よって
(1-8)$\qquad E_1 = (y_1 - \hat{y_1})^2 = (y_1 - (0.75x_1 - 2))^2$
(1-9)$\qquad E_2 = (y_2 - \hat{y_2})^2 = (y_2 - (0.75x_2 - 2))^2$
と書くことができて、実際の $x$, $y$ をあてはめてみると、
(1-10)$\qquad E_1 = (2 - (0.75 * 4 - 2))^2 = (2 - 1)^2 = 1$
(1-11)$\qquad E_2 = (3 - (0.75 * 8 - 2))^2 = (3 - 4)^2 = (-1)^2 = 1$
(1-12)$\qquad E = E_1 + E_2 = 1 + 1 = 2$
となって、
(1-5), (1-6), (1-7) の式と同じことが確認できました。
さて、$(0.75x -2)$ の部分は $x$ の関数なので、$f(x)$ と表すことができます。それで $E$ を求めた式を書き換えると
\begin{align}
E &= E_1 + E_2 \\
\\
&= (y_1 - \hat{y_1})^2 + (y_2 - \hat{y_2})^2 \\
\\
&= (y_1 - f(x_1))^2 + (y_2 - f(x_2))^2
\end{align}
となって異なるのは添え字の部分だけなのでこれは、
(1-13)$\qquad E = \sum_{i=1}^n(y_i - f(x_i))^2$
と書き表せます。
これで誤差を計算するための一般化された式が手に入りました。この式の $y$ と $x$ に値を代入して計算すれば誤差(の合計)が求まりますね。って、いやいや、いま僕らが求めたいのは $a$ とか $b$ とか($w$ とか $b$ とか $w_1$ とか $w_0$ とか)ってパラメータだったはず。あやうく目先の $y$ とか $x$ に意識が向いちゃうとこでしたよ。
というわけで、本来の目的を意識しつつもうちょっと変形してみましょう。
パラメータを求めるように変形する
というわけで、この(1-13)の式をもうちょっと変形すると
(1-14)
\begin{align}
E &= \sum(y_i - f(x_i))^2 \\
\\
&= (y_1 - f(x_1))^2 + (y_2 - f(x_2))^2 \\
\\
&= (y_1 - (ax_1 + b))^2 + (y_2 - (ax_2 + b))^2
\end{align}
になります。
で、$x_1$, $y_1$, $x_2$, $y_2$ は今回、
| x | y | |
|---|---|---|
| データ 1 | 4 | 2 |
| データ 2 | 8 | 3 |
こんな風にデータとして値が与えられているので、$x_1 = 4$, $y_1 = 2$, $x_2 = 8$, $y_2 = 3$ を (1-14) にそれぞれ代入すると、
(1-15)
\begin{align}
E &= (2 - (a * 4 + b))^2 + (3 - (a * 8 + b))^2 \\
\\
&= (2 - (4a + b))^2 + (3 - (8a + b))^2
\end{align}
(1-15) の一項めを $E_1$, 二項めを $E_2$ とすると、
(1-16)
\begin{align}
E_1 &= (2 - (4a + b))^2 \\
\\
4a + b &= A とおくと \\
\\
E_1 &= (2 - A)^2 \\
\\
&= 4 - 4A + A^2 \\
\\
&A を元に戻して \\
\\
&= 4 - 4(4a + b) + (4a + b)^2 \\
\\
&= 4 - 16a - 4b + 16a^2 + 8ab + b^2
\end{align}
同様に
(1-17)
\begin{align}
E_2 &= (3 - (8a + b))^2 \\
\\
&= (3 - B)^2 \\
\\
&= 9 -6B + B^2 \\
\\
&= 9 - 6(8a + b) + (8a + b)^2 \\
\\
&= 9 - 48a - 6b + 64a^2 + 16ab + b^2
\end{align}
よって
(1-18)
\begin{align}
E &= E_1 + E_2 \\
\\
&= (4 - 16a - 4b + 16a^2 + 8ab + b^2) + (9 - 48a - 6b + 64a^2 + 16ab + b^2) \\
\\
&= 13 - 64a - 10b + 80a^2 + 24ab + 2b^2
\end{align}
になって、この $E$ が最小(ゼロ)になる $a$, $b$ を求めればそれが最適なパラメータとなるはずですね。
ここでこの
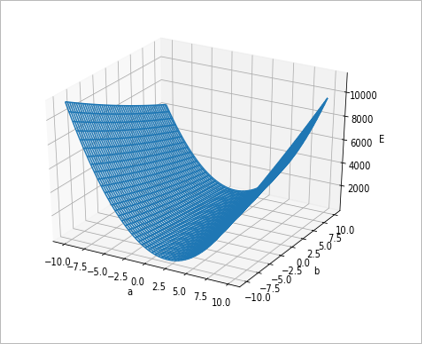
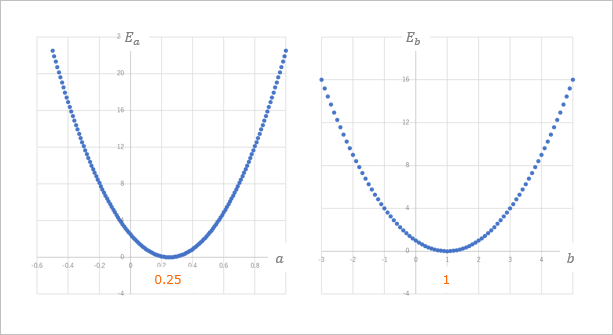
(1-19)$\qquad E = 13 - 64a - 10b + 80a^2 + 24ab + 2b^2$
をグラフで描いてみると
のような3次元のグラフになります。このグラフの最も低い点がすなわち、$E$ が 最小 になる点で、ここにあたる $a$, $b$ を求められれば、$E$ を最小にできますね。
偏微分する?
さて、これは最小化問題なので、微分すればよさそうです。ただ、今回は $a$, $b$ と2つの未知数があるので、さてどうしましょうか…
まぁ、偏微分すればいいんですけどね。偏微分っていってもここでやるのは単に注目している変数($a$ もしくは $b$)以外は定数として扱うってことぐらいなので、まったく難しいものではありません。ってわけで、偏微分してみましょうか。
(1-20)$\qquad \frac{\partial E}{\partial a} = 0 - 64 - 0 + 160a + 24b + 0 = 160a + 24b -64$
(1-21)$\qquad \frac{\partial E}{\partial b} = 0 - 0 - 6 + 0 + 16a + 2b = 16a + 2b - 6$
この二つの式の連立方程式を解くと、
$\qquad a = 0.25$, $b = 1$
となって、おめでとう!解析的に求めた解と一致しました!ということでこの方法で計算すれば正しいパラメータが得られますね!ね?
うん、、確かに求められたけど、さっき適当に決めたパラメータって何だったんでしたっけ?誤差関数のグラフとの関係って何なんでしたっけ?なんか適当にパラメータを決めて誤差を限りなくゼロに近づけていって限りなく正しいパラメータを推定するって話とどう関係するんでしたっけ?結局のところ、これだと最初に解析的に求めたのとあまり変わらないですよね。
私はなんとかしてこの図の左側の求めたいパラメータのグラフと右側の誤差関数のグラフとの関係性についてわかりたいのに、これじゃあ意味がありません。どう関係してるかさっぱりわかりません。いやさっぱりということはないですが、いまひとつイメージできません。や、だって3次元のグラフだし。。というわけで、私にも何とか理解できるレベルで話を進めないとダメですね。
さてズルをしましょう
ということで、ここでちょっとだけズルをしてみます。
いま、$a$, $b$ の2つのパラメータを求めたいと思っていて、誤差関数に実際のデータを当てはめて展開してみると、未知数が $a$, $b$ の2つある関数になっちゃいました(1-19)。で、ちょっとこのままだとなんなので(なんなので?)ちょっとズルをして片方のパラメータはすでにわかっているってことにしちゃえば、あと残り1つを求めればいいってことになりますね。幸いにも解析的に正しいパラメータはわかっているので、まぁ、どっちかのパラメータをあてはめちゃえばいいんじゃないでしょうか。
ってことで、手始めに $b$ がわかってるってことにしてみましょう。んで、$a$ を求めてみる。と。
解析的に $b = 1$ なので、さっきの誤差関数を展開した式に $b = 1$ を代入してみましょう。
(1-19)より、
(1-22)
\begin{align}
E &= 13 - 64a - 10b + 80a^2 + 24ab + 2b^2 \\
\\
E_{a(b=1)} &= 13 - 64a - (10 * 1) + 80a^2 + (24a * 1) + 2 * 1^2 \\
\\
&= 13 - 64a - 10 + 80a^2 + 24a + 2 \\
\\
&= 80a^2 -40a + 5
\end{align}
$a$ にフォーカスした誤差関数なので、$E_a$ としてあります。(これはたぶんここだけの書き方で一般的な書き方ではないです。)
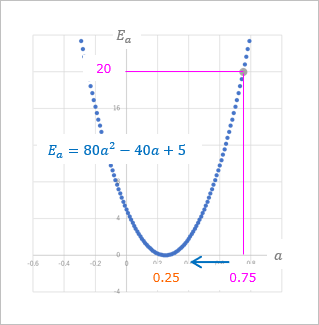
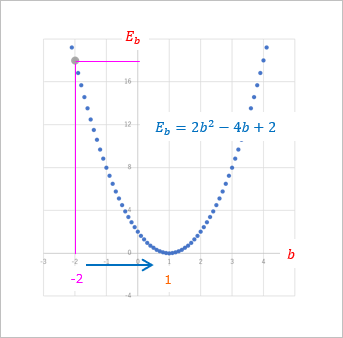
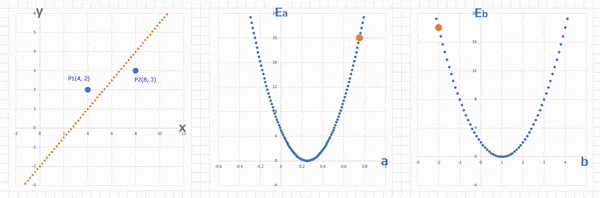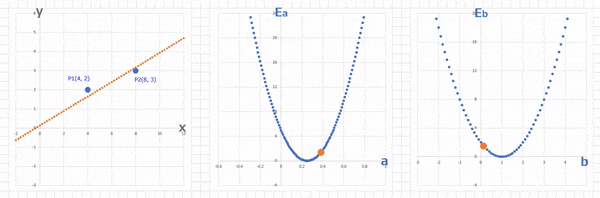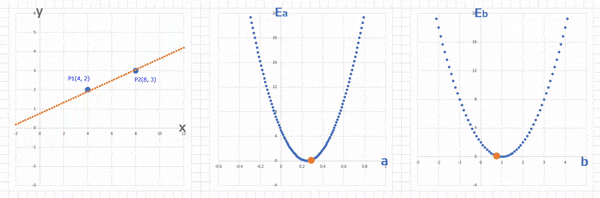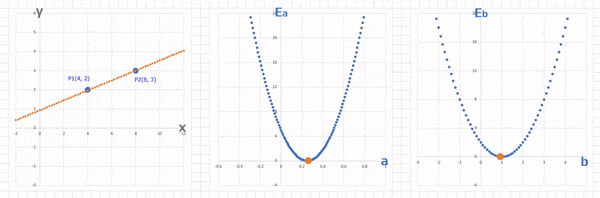
これをグラフで描くとこのようになります。
横軸が $a$, 縦軸が $E_a$ となっていて、$a$ に関する関数になっています。
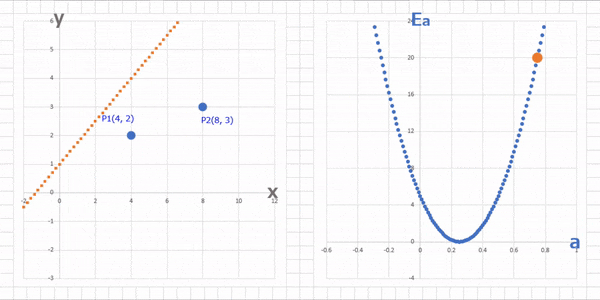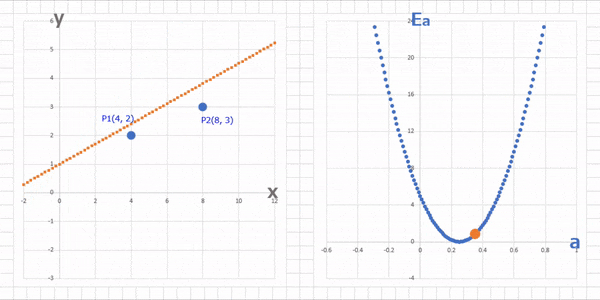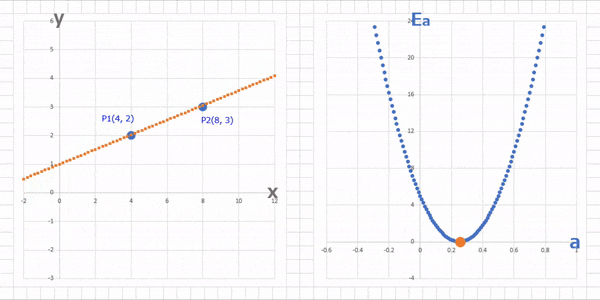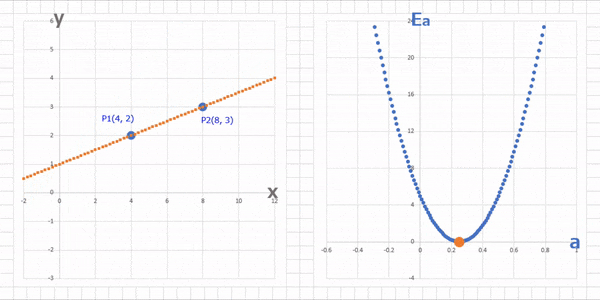
このグラフでさっき適当に決めた $a = 0.75$ における $E_a$ は
(1-23)$\qquad E_{a(a=0.75, b=1)} = 80 * 0.75^2 - (40 * 0.75) + 5 = 20$
ということで、適当に決めた $a = 0.75$ のときのグラフ上の点は $P(0.75 , 20)$ という位置にあって、この $E_a = 20$ を $0$ に近づけるには、$a$ を $0.25$に近づけていけばいいということがわかります。うん、わかった。で、どうやって「近づけていく」の?
(補足:E が (1-12) で求めた 2 にならないのは b = 1 としているため)
\begin{align}
E_1 &= (y_1 - (ax_1 + b))^2 \\
&= (2 - (0.75 * 4 + 1))^2 \\
&= (2 - 4)^2 \\
&= 4 \\
\\
E_2 &= (y_2 - (ax_2 + b))^2 \\
&= (3 - (0.75 * 8 + 1))^2 \\
&= (3 - 7)^2 \\
&= 16 \\
\\
E_a &= E_1 + E_2 = 4 + 16 = 20
\end{align}
接線の傾きを求めよう
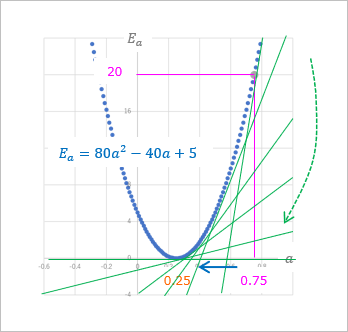
上の図の誤差関数で $a = 0.75$ の接線の傾きはけっこう大きいですが、これが $a$ の正しい値 $a = 0.25$ に近づくにつれて小さくなっていきます。図にするとこんな感じ。緑色の線の傾きに注目です。
そんなわけで、接線の傾きを調べるのですが、接線の傾きを調べると言えばアレです。微分です。微分で求めることができますね。最小化問題で「最小化問題なので微分」って言ってるアレですよ。
というわけで微分してみましょう。何を微分するかというと、$E_a$ の接線を求めるのでこの2次元のグラフ $E_a$ の式です。
(1-22)より
$\qquad E_a = 80a^2 - 40a + 5$
なので
(1-24)$\qquad \frac{d E_a}{d a} = \frac{d}{d a}(80a^2 - 40a + 5) = 160a - 40$
じゃあ、この $a$ に適当に値を入れていってみましょうか。
$\qquad a = 0.75$ のとき $160 * 0.75 - 40 = 120 - 40 = 80$
$\qquad a = 0.50$ のとき $160 * 0.50 - 40 = 80 - 40 = 40$
$\qquad a = 0.25$ のとき $160 * 0.25 - 40 = 40 - 40 = 0$
$\qquad a = 0.00$ のとき $160 * 0.00 - 40 = 0 - 40 = -40$
$\qquad a = -0.25$ のとき $160 * -0.25 - 40 = -40 - 40 = -80$
$\qquad …$
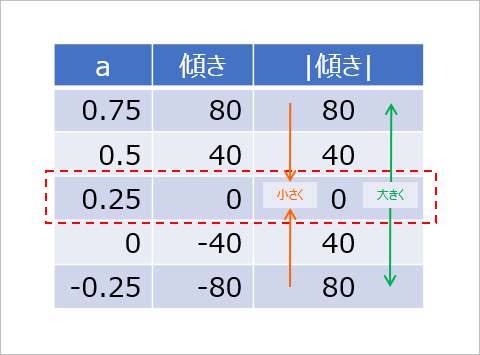
となって、傾きが $0$ になる $a = 0.25$ に対して、傾きがプラスの場合($80$ とか $40$ とか)は $a$ を小さくしていく($0.75 \rightarrow 0.50 \rightarrow 0.25$)マイナスの場合($-40$ とか $-80$ とか)は $a$ を大きくしていく($-0.25 \rightarrow 0.00 \rightarrow 0.25$)ことで、$0.25$ に近づけていけることがわかりますね。
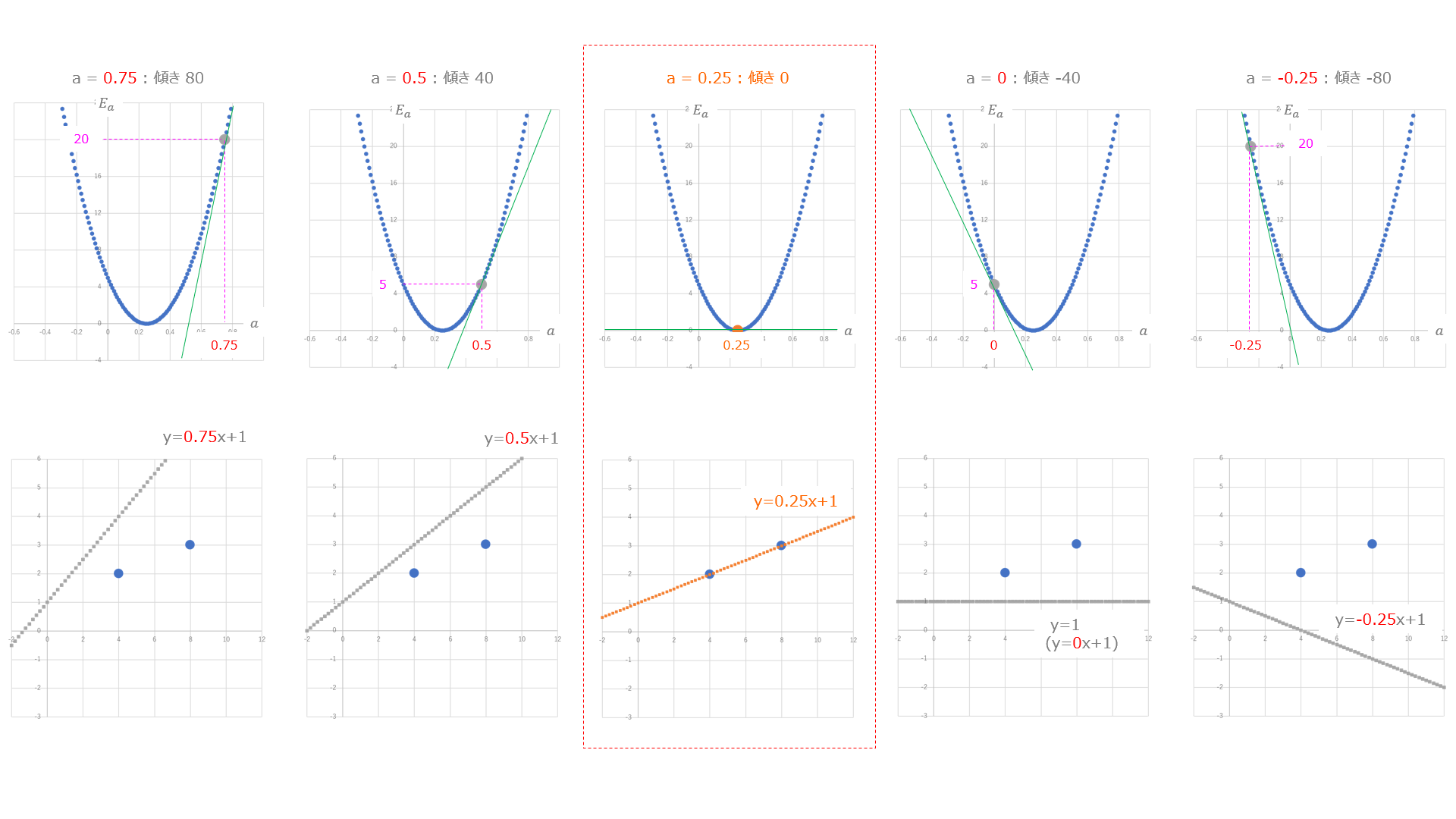
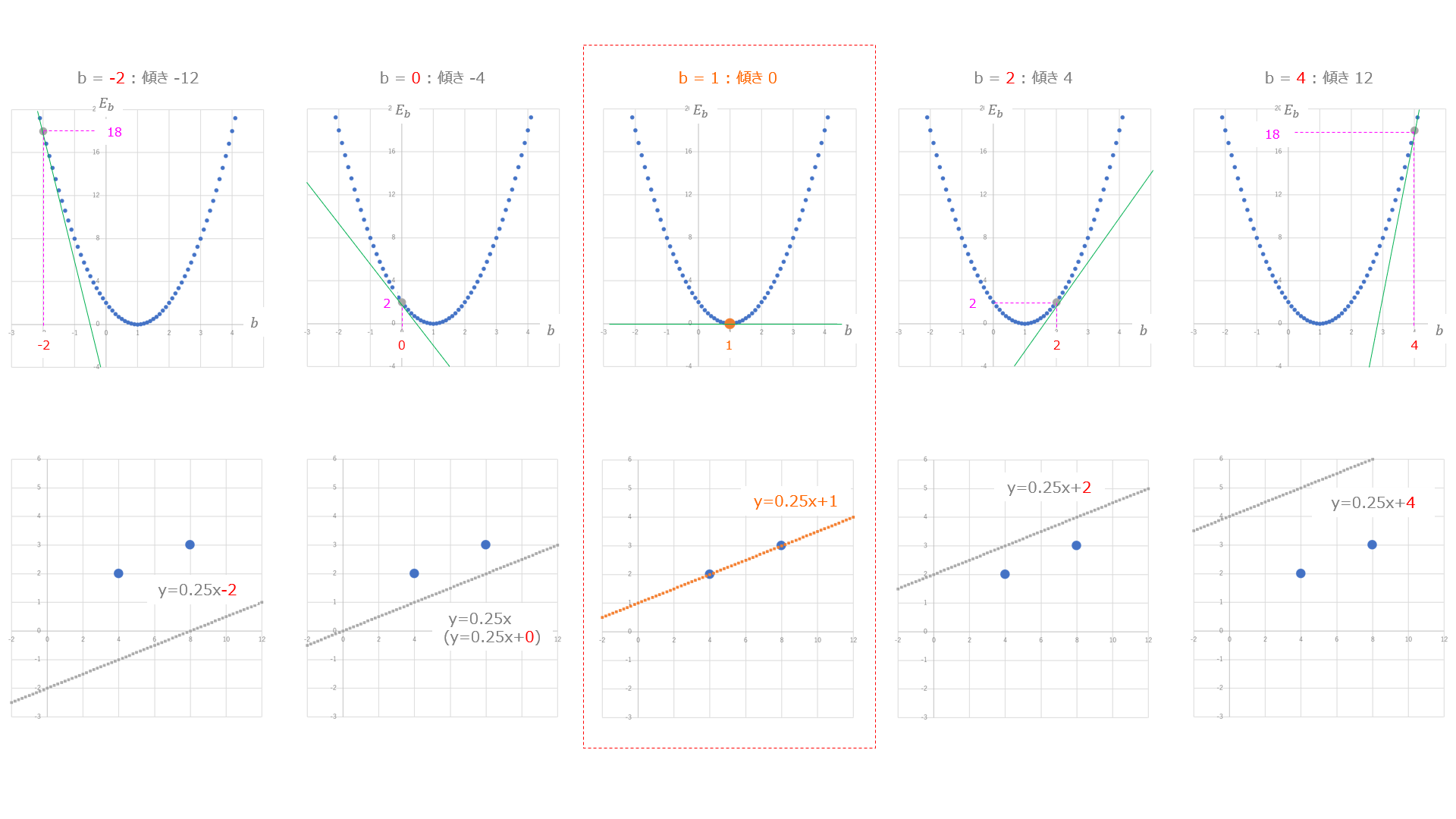
この様子をグラフで見てみましょう。
上のグラフが誤差関数で $a$ の値を変えていったときの傾きと $E_a$ の値を表したもの。下のグラフはそのときのパラメータ $a$ での(求めたい)直線を表したものです。今回切片 $b$ は $1$ に固定しているんでしたね。
これこれ!冒頭に出てきた求めたいグラフと誤差関数のグラフの関係がわからないって話、この上下のグラフを比べると関係性が見えてきますね。つまり、誤差関数の最小となる点のパラメータがわかれば、これが求めたいグラフのパラメータ(今回は傾き)になるわけです。
これを動画でみてみるとこんな感じになります。右側のオレンジの玉が「勾配」を「降下」して誤差関数の谷底に近づくにつれて左側のオレンジの直線が青い点に近づいていきます。
パラメータ a を求める式を考えよう
さて、誤差関数における接線の傾きとパラメータの関係がなんとなく見えてきたので、この関係性を使ってパラメータ $a$ をよりよいパラメータ $a$ に調整していってみましょう。いまは $a = 0.75$ と適当に決めちゃってるので、そこからスタートして最終的には解析的に求めた $a = 0.25$ になればいいですよね。
上の計算とグラフで見たように、傾きが 0 になるポイントに対して、傾きがプラスの場合は $a$ を小さく、マイナスの場合は $a$ を大きくしていくと、だんだんと正しいパラメータ $a$ に近づいていきます。それを踏まえて $a$ を更新する式を考えてみると
(1-25)$\qquad$ 更新後の $a$ = 更新前の $a$ - (傾きの符号 * なんらかの値)
という式にすればよさそうな気がします。
更新前の$a$ から(傾きの符号 * 何らかの値)を引いているのは、
傾きがプラスの場合
$\qquad$ 更新前の$a$ - (+何らかの値)$\Rightarrow$ 更新前の$a$ - 何らかの値
となって
傾きがマイナスの場合
$\qquad$ 更新前のa - (-何らかの値)$\Rightarrow$ 更新前の$a$ + 何らかの値
となるので、傾きがプラスのときは $a$ を小さく、マイナスのときには $a$ を大きくしたいという意図に沿うためです。
「なんらかの値」ってなんだ?
とりあえずこんな計算式で計算すれば $a$ が更新されていくっぽいことがなんとなくわかったけど「なんらかの値」って何?これがわからないと更新しようがないんですけど。ということで、さっきのグラフを見ると、$a$ の正しい値 $0.25$ から遠ざかるにつれて傾き(の絶対値)は大きく、近づくにつれて小さくなっていってるのがわかると思います。表にするとこんな感じ。
というわけで、この傾きの値を使っていけばいいんじゃないでしょうか。
傾きの値を求める式は
(1-24) より
(1-26)$\qquad \frac{dE_a}{da} = 160a - 40$
だったので、(1-25)の「なんらかの値」の部分をこの式にしてみることを考えると、傾きを求めたときにプラスとかマイナスもついていたので、「傾きの符号」の部分も(1-26)の式で表せちゃいます。というわけで、
(1-27)$\qquad$ 更新後の $a$ = 更新前の $a$ - (傾きの符号 * なんらかの値)
$\qquad\qquad\qquad\qquad\quad$ = 更新前の $a$ - ($160$ * 更新前の $a$ - $40$)
となったので、これに実際に値を当てはめて計算していってみましょう。
とりあえず計算してみよう
まずは、今回とりあえず適当に $a = 0.75$ と設定しているので、更新前の値として $a = 0.75$ で計算してみます。
1回目:$0.75 - (160 * 0.75 - 40) = -79.25$ (= 更新後の $a$)
2回目:$-79.25 - (160 * -79.25 - 40) = 12640.75$
3回目:$12640.75 - (160 * 12640.75 - 40) = -2009839$
というわけで、ぜんぜん正しい値の $0.25$ には近づきそうにありません。。
たぶん、「なんらかの値」が大きすぎるからだと思うので、これをちょっと調整してみましょう。
なんらかの値をちょっと調整して計算しなおしてみよう
手始めとして $0.01$ を掛けてみることにします。
1回目:$0.75 - ((160 * 0.75 - 40) * 0.01) = -0.05$
2回目:$-0.05 - ((160 * -0.05 - 40) * 0.01) = 0.43$
3回目:$0.43 - ((160 * 0.43 - 40) * 0.01) = 0.142$
4回目:$0.142 - ((160 * 0.142 - 40) * 0.01) = 0.3148$
5回目:$0.3148 - ((160 * 0.3148 - 40) * 0.01) = 0.21112$
いい感じですね。
22回目:$0.249989 - ((160 * 0.249989 - 40) * 0.01) = 0.250007$
23回目:$0.250007 - ((160 * 0.250007 - 40) * 0.01) = 0.249996$
24回目:$0.249996 - ((160 * 0.249996 - 40) * 0.01) = 0.250002$
という感じで、大きくなったり小さくなったりしながらも、徐々に $0.25$ に近づいて行ってますね。いい感じです!
では、$0.001$ を掛けてみるとどうなるでしょう?
1回目:$0.75 - ((160 * 0.75 - 40) * 0.001) = 0.67$
2回目:$0.67 - ((160 * 0.67 - 40) * 0.001) = 0.6028$
3回目:$0.6028 - ((160 * 0.6028 - 40) * 0.001) = 0.546352$
…
22回目:$0.262848 - ((160 * 0.262848 - 40) * 0.001) = 0.260792$
23回目:$0.260792 - ((160 * 0.260792 - 40) * 0.001) = 0.259066$
24回目:$0.259066 - ((160 * 0.259066 - 40) * 0.001) = 0.257615$
…
60回目:$0.250017 - ((160 * 0.250017 - 40) * 0.001) = 0.250014$
61回目:$0.250014 - ((160 * 0.250014 - 40) * 0.001) = 0.250012$
この場合も、回数は多くかかってますが、やっぱり徐々に $0.25$ に近づいて行ってます。
というわけで、パラメータの更新に使う「なんらかの値」は「接線の傾き」に $0.01$ とか $0.001$ とかの調整値を掛けて小さくした値を用いればよさそうです。
ほんとに?
今回は $b$ を $1$ に固定して $a$ を更新していったけど、その逆ってまだやってませんよね。そっちも同じ考えで大丈夫か確認しておいた方がいいかもですね。
今度は b を更新してみよう
さて、解析的に $a = 0.25$ とわかっているので、今度はこれを使って $b$ の更新をやってみましょう。
(1-19)に $a = 0.25$ を代入して b にフォーカスした誤差関数 $E_b$ の式を求めてみます。
(1-19)より、
(1-28)
\begin{align}
E &= 13 - 64a - 10b + 80a^2 + 24ab + 2b^2 \\
\\
E_{b(a=0.25)} &= 13 - 64 * 0.25 - 10b + (80 * 0.25^2) + (24b * 0.25) + 2b^2 \\
\\
&= 13 - 16 - 10b + 5 + 6b + 2b^2 \\
\\
&= 2b^2 -4b + 2
\end{align}
これをグラフで描くとこのようになります。
今回は、横軸が $b$, 縦軸が $E_b$ となっていて、$b$ に関する関数になっています。
今回、$b$ の適当な値としては $-2$ にしていたので、このグラフでこの適当に決めた $b = -2$ における $E_b$ を見てみると
(1-29)$\qquad E_{b(a=0.25, b=-2)} = 2 * (-2)^2 - 4 * (-2) + 2 = 18$
ということで、適当に決めた $b = -2$ のときのグラフ上の点は $P(-2 , 18)$ という位置にあって、この $E_b = 18$ を $0$ に近づけるには、$b$ を $1$ に近づけていけばいいということがわかりますね。($a$ のときと同じ考え方です。)
$a$ のときはどうしたんでしたっけ?あぁ、この $E_b$ の式を微分したんでしたね。
(1-28)より
$\qquad E_b = 2b^2 -4b + 2$
なので
(1-30)$\qquad \frac{dE_b}{db} = \frac{d}{db}(2b^2 -4b + 2) = 4b - 4$
傾きを調べよう
じゃあ、この式に適当に $b$ の値を入れていってその時の接線の傾きを調べてみましょう。
$\qquad b = -2$ のとき $4 * -2 - 4 = -12$
$\qquad b = 0$ のとき $4 * 0 - 4 = -4$
$\qquad b = 1$ のとき $4 * 1 - 4 = 0$
$\qquad b = 2$ のとき $4 * 2 - 4 = 4$
$\qquad b = 4$ のとき $4 * 4 - 4 = 12$
というようになって、$a$ のときと同様に、正しい $b$ の値 $b = 1$ に対して、傾きがマイナスの場合は $b$ を大きく、プラスの場合は小さくしていけば正しい $b = 1$ に近づくことがわかりますね。
グラフで表すとこんな感じ。
$a$ のときと同様、動画で見てみましょう。こんな感じになります。
$b$ も $a$ と同様の更新式で更新していってみましょう。
(1-31)$\qquad$ 更新後の $b$ = 更新前の $b$ - (接線の傾き * 調整値)
$\qquad\qquad\qquad\qquad\quad$ = 更新前の $b$ - (($4$ * 更新前の $b$ - $4$) * 調整値)
実際にbを更新していってみる
では、先ほど同様、調整値を $0.01$ で $b$ を更新していってみましょう。今回 $b$ は適当に $-2$ としているので、$-2$ から始めます。
1回目:$-2 - ((4 * -2 - 4) * 0.01) = -1.88$
2回目:$-1.88 - ((4 * -1.88 - 4) * 0.01) = -1.7648$
3回目:$-1.7648 - ((4 * -1.7648 - 4) * 0.01) = - 1.65421$
290回目:$0.999977 - ((4 * 0.999977 - 4) * 0.01) = 0.999978$
291回目:$0.999978 - ((4 * 0.999978 - 4) * 0.01) = 0.999979$
292回目:$0.999979 - ((4 * 0.999979 - 4) * 0.01) = 0.999980$
いい感じで $1$ に近づいていってますね。
今度は $0.001$ で計算してみましょう。
1回目:$-2 - ((4 * -2 - 4) * 0.001) = -1.988$
2回目:$-1.988 - ((4 * -1.988 - 4) * 0.001) = -1.97605$
3回目:$-1.97605 - ((4 * -1.97605 - 4) * 0.001) = -1.96414$
290回目:$0.057958 - ((4 * 0.057958 - 4) * 0.001) = 0.061727$
291回目:$0.061727 - ((4 * 0.061727 - 4) * 0.001) = 0.065480$
292回目:$0.065480 - ((4 * 0.065480 - 4) * 0.001) = 0.069218$
1000回目:$0.945273 - ((4 * 0.945273 - 4) * 0.001) = 0.945492$
1001回目:$0.945492 - ((4 * 0.945492 - 4) * 0.001) = 0.945927$
1002回目:$0.945927 - ((4 * 0.945927 - 4) * 0.001) = 0.946144$
こちらも回数は多いですが $1$ に近づいていってます。
ということで、$b$ の更新も $a$ の更新と同様の式で行えることがわかりました!
(補足:更新するときの値を等間隔にしちゃえば微分とか面倒な計算はいらないんじゃない?)
$a$ の更新のときに、一定の値を引くか足すかしていった方が、いちいち傾きの計算をしなくて楽なんじゃない?
例えば、$0.1$ を引いていくと
1回目:$0.75 - 0.1 = 0.65$
2回目:$0.65 - 0.1 = 0.55$
3回目:$0.55 - 0.1 = 0.45$
ってやっていけば、確実に $0.25$ に近づいていきますよね。
ただ、このままこの計算を続けていくと、
4回目:$0.45 - 0.1 = 0.35$
5回目:$0.35 - 0.1 = 0.25$
6回目:$0.25 - 0.1 = 0.15$
7回目:$0.15 - 0.1 = 0.05$
あらら、$0.25$ を通り過ぎちゃったじゃないですか…
いいところで止める判断をしないとダメですね。
あと、一定量が本当に $0.1$ でいいのか、ほかの値の方がいいのかって問題もあるし…
かえって考えることが増えそうな感じです。
微分を使った更新式の場合は、自動的に(?)正しい値に近づいていってくれるので、一見複雑そうな計算ですが、「判断すること」はあまりなさそうです。「判断すること」が多いとそれだけ実装が面倒なので、なるべく自動で調整してくれた方がいいですよね。
じゃあ、 a と b を一緒に考えてみることにしましょうか
いままでは $a$ か $b$ のどちらかを固定してみていってましたが、本来はそのどちらも未知なためそういうわけにはいかないですよね。ということで、ここからは $a$ も $b$ も未知として話を進めていきましょう。
さて、ずっとさかのぼって
(1-14)より
(1-32)
\begin{align}
E &= \sum(y_i - f(x_i))^2 \\
\\
&= (y_1 - f(x_1))^2 + (y_2 - f(x_2))^2 \\
\\
&= (y_1 - (ax_1 + b))^2 + (y_2 - (ax_2 + b))^2 \\
\\
\end{align}
だったので、この第1項($E_1$ とします)と第2項($E_2$ とします)をそれぞれ展開してみます。
前回 ((1-16), (1-17)) は $y$ や $x$ に具体的な値を入れて計算しましたが、今回はこのまま展開します。
(1-33)
\begin{align}
E_1 &= (y_1 - (ax_1 + b))^2 \\
\\
&= (y_1 - A)^2 \\
\\
&= y_1^2 - 2y_1A + A^2 \\
\\
&= y_1^2 - 2y_1(ax_1 + b) + (ax_1 + b)^2 \\
\\
&= y_1^2 - 2ax_1y_1 -2by_1 + a^2x_1^2 + 2abx_1 + b^2
\end{align}
(1-34)
\begin{align}
E_2 &= (y_2 - (ax_2 + b))^2 \\
\\
&= y_2^2 - 2ax_2y_2 -2by_2 + a^2x_2^2 + 2abx_2 + b^2 \\
\\
\end{align}
$E = E_1 + E_2 = …$ なのですが、無駄に複雑になるので今回はこのまま話を進めます。
前回まででは、(1-24) や (1-30) では、それぞれ $a$, $b$ に注目したいために、具体的な値($x_1$, $y_1$, $x_2$, $y_2$, $a$ or $b$)を代入してそれぞれで微分して接線の傾きを求める式を求めましたが、今回は $a$ と $b$ の両方をいっぺんに求めたいのです。なので、$a$, $b$ はそのまま扱う必要があるのですが、$E_1$, $E_2$ にはそれぞれで $a$, $b$ が含まれています。この式を微分するので、偏微分を使って式を求めていきます。
偏微分してみる
まずは $E_1$ を $a$ で偏微分してみましょう。
(1-35)
\begin{align}
\frac{\partial E_1}{\partial a} &= \frac{\partial}{\partial a}(y_1^2 - 2ax_1y_1 -2by_1 + a^2x_1^2 + 2abx_1 + b^2) \\
\\
&= 0 - 2x_1y_1 - 0 + 2ax_1^2 + 2bx_1 + 0 \\
\\
&= 2x_1((ax_1 + b) - y_1)
\end{align}
$E_2$ は
(1-36)
\begin{align}
\frac{\partial E_2}{\partial a} &= \frac{\partial}{\partial a}(y_2^2 - 2ax_2y_2 -2by_2 + a^2x_2^2 + 2abx_2 + b^2) \\
\\
&= 0 - 2x_2y_2 - 0 + 2ax_2^2 + 2bx_2 + 0 \\
\\
&= 2x_2((ax_2 + b) - y_2)
\end{align}
となりました。
添え字が違うだけなので $\sum$ でまとめられますね。
ということで、
(1-37)
\begin{align}
\frac{\partial E}{\partial a} &= \frac{\partial E_1}{\partial a} + \frac{\partial E_2}{\partial a} \\
\\
&= 2x_1((ax_1 + b) - y_1) + 2x_2((ax_2 + b) - y_2) \\
\\
&= 2\sum((ax_i + b) - y_i) * x_i
\end{align}
(機械学習とかで見覚えのある数式がでてきましたね!)
じゃあ、今度は $b$ について
(1-38)
\begin{align}
\frac{\partial E_1}{\partial b} &= \frac{\partial}{\partial b}(y_1^2 - 2ax_1y_1 -2by_1 + a^2x_1^2 + 2abx_1 + b^2) \\
\\
&= 0 - 0 - 2y_1 + 0 + 2ax_1 + 2b \\
\\
&= 2((ax_1 + b) - y_1)
\end{align}
(1-39)
\begin{align}
\frac{\partial E_2}{\partial b} &= \frac{\partial}{\partial b}(y_2^2 - 2ax_2y_2 -2by_2 + a^2x_2^2 + 2abx_2 + b^2) \\
\\
&= 2((ax_2 + b) - y_2)
\end{align}
なので、
(1-40)
\begin{align}
\frac{\partial E}{\partial b} &= \frac{\partial E_1}{\partial b} + \frac{\partial E_2}{\partial b} \\
\\
&= 2((ax_1 + b) - y_1) + 2((ax_2 + b) - y_2) \\
\\
&= 2\sum((ax_i + b) - y_i)
\end{align}
(また見覚えのある数式が!)
これでそれぞれのパラメータの更新で使う式がわかりました。
更新の式の「接線の傾きを求める」式の部分ですね。「なんらかの値」とかいってたあの部分です。
ほんとにこれって正しいの?
いちおう、上記のように求まりましたが、これって本当に正しいんでしょうかね。。
念のため確認してみることにしましょう。
前に $a$ に注目していた時は $b = 1$ として計算したので、今回もそれで試してみます。
(1-37) に $b = 1$ を代入するとどうなるか見てみましょう。
ついでに、$x_1 = 4$, $y_1 = 2$, $x_2 = 8$, $y_2 = 3$ も代入してみます。
(1-41)
\begin{align}
2\sum((ax_i + b) - y_i) * x_i &= 2((((a * x_1 + b) - y_1) * x_1) + (((a * x_2 + b) - y_2) * x_2)) \\
\\
&= 2((((a * 4 + 1) - 2) * 4) + (((a * 8 + 1) - 3) * 8)) \\
\\
&= 2((4a - 1) * 4 + (8a - 2) * 8) \\
\\
&= 2(16a - 4 + 64a - 16) \\
\\
&= 2(80a - 20) \\
\\
&= 160a - 40
\end{align}
となって、(1-24)で求めたのと同じになりました。
同様に $b$ についての式も見ておきましょう。
(1-40) に $a = 0.25$ を代入してみます。
(1-42)
\begin{align}
2\sum((ax_i + b) - y_i) &= 2(((a * x_1 + b) - y_1) + (a * x_2 + b) - y_2)) \\
\\
&= 2(((0.25 * 4 + b) - 2) + ((0.25 * 8 + b) - 3)) \\
\\
&= 2((1 + b - 2) + (2 + b - 3)) \\
\\
&= 2(2b - 2) \\
\\
&= 4b - 4
\end{align}
となって、(1-30) で求めたのと同じになりました。
よって、どうやらこの式は正しそうだということがわかりましたね。
a と b の本当の更新式
さて、誤差関数の式を求めたいパラメータ $a$, $b$ で偏微分した式がわかりました。
以前それぞれの更新式を求めたときに「なんらかの値」とか「接線の傾き」とかいっていた部分なので、それぞれの更新式はこんな風にあらわせますね。
(1-43)$\qquad$ 更新後の $a$ = 更新前の $a$ - (誤差関数を $a$ で偏微分した式 * 調整値)
$\qquad\qquad\qquad\qquad\quad$ = 更新前の $a$ - ($\frac{\partial E}{\partial a}$ * 調整値)
$\qquad\qquad\qquad\qquad\quad$ = 更新前の $a$ - (2$\sum$((更新前の $a$ * $x_i$ + $b$) - $y_i$) * $x_i$) * 調整値
(1-44)$\qquad$ 更新後の $b$ = 更新前の $b$ - (誤差関数を $b$ で偏微分した式 * 調整値)
$\qquad\qquad\qquad\qquad\quad$ = 更新前の $b$ - ($\frac{\partial E}{\partial b}$ * 調整値)
$\qquad\qquad\qquad\qquad\quad$ = 更新前の $b$ - ($2\sum$((更新前の $b$ * $x_i$ + $b$) - $y_i$) * 調整値
やった!やりました!ついに欲しかった更新式が手に入りましたよ!
本当に更新されるか試してみる
まぁ、私はけっこううたぐり深いので本当にこれで更新されるのかってのが気になっちゃうんですよね。なりません?
というわけで実際に数値を入れて確かめてみましょう。
ただ、その前にこのままではいろいろ計算が面倒なのでそれぞれの偏微分の部分の式をちょっと簡単にしましょう。
$x_1$, $y_1$, $x_2$, $y_2$ はデータとして与えられているので、あらかじめこれを代入しておきます。
| x | y | |
|---|---|---|
| データ 1 | 4 | 2 |
| データ 2 | 8 | 3 |
(1-37)より
(1-45)
\begin{align}
\frac{\partial E}{\partial a} &= 2\sum((ax_i + b) - y_i) * x_i \\
\\
&= 2((((a * 4 + b) - 2) * 4) + (((a * 8 + b) - 3) * 8)) \\
\\
&= 2(((4a + b - 2) * 4) + ((8a + b - 3) * 8)) \\
\\
&= 2(16a + 4b - 8 + 64a + 8b - 24) \\
\\
&= 2(80a + 12b - 32) \\
\\
&= 160a + 24b - 64
\end{align}
(1-40)より
(1-46)
\begin{align}
\frac{\partial E}{\partial b} &= 2\sum((ax_i + b) - y_i) \\
\\
&= 2((a * 4 + b - 2) + (a * 8 + b - 3)) \\
\\
&= 2(4a + b - 2 + 8a + b - 3) \\
\\
&= 2(12a + 2b - 5) \\
\\
&= 24a + 4b - 10
\end{align}
これを使って
(1-43)より
(1-47)$\qquad$ 更新後の $a$ = 更新前の $a$ - (誤差関数を $a$ で偏微分した式 * 調整値)
$\qquad\qquad\qquad\qquad\quad$ = 更新前の $a$ - ($\frac{\partial E}{\partial a}$ * 調整値)
$\qquad\qquad\qquad\qquad\quad$ = 更新前の $a$ - ($160a$ + $24b$ - $64$) * 調整値
(1-44)より
(1-48)$\qquad$ 更新後の $b$ = 更新前の $b$ - (誤差関数を $b$ で偏微分した式 * 調整値)
$\qquad\qquad\qquad\qquad\quad$ = 更新前の $b$ - ($\frac{\partial E}{\partial b}$ * 調整値)
$\qquad\qquad\qquad\qquad\quad$ = 更新前の $b$ - ($24a$ + $4b$ - $10$) * 調整値
この式で計算していきましょう。
なお、今回の調整値は $0.01$ にしてみます。
ついでに以下の式で $E$ の値も計算してみましょう。
(1-32)より
$\qquad E = (y_1 - (ax_1 + b))^2 + (y_2 - (ax_2 + b))^2$
さて、例によって $a = 0.75$, $b = -2$ からスタートです。
1回目
$\qquad a: 0.75 - (160 * 0.75 + 24 * (-2) - 64) * 0.01 = 0.67$
$\qquad b: -2 - (24 * 0.75 + 4 * (-2) - 10) * 0.01 = -2$
$\qquad E: (2 - (0.75 * 4 + (-2)))^2 + (3 - (0.75 * 8 + (-2)))^2 = 2$
2回目
$\qquad a: 0.67 - (160 * 0.67 + 24 * (-2) - 64) * 0.01 = 0.718$
$\qquad b: -2 - (24 * 0.67 + 4 * (-2) - 10) * 0.01 = -1.9808$
$\qquad E: (2 - (0.67 * 4 + (-2)))^2 + (3 - (0.67 * 8 + (-2)))^2 = 1.872$
3回目
$\qquad a: 0.718 - (160 * 0.718 + 24 * (-1.9808) - 64) * 0.01 = 0.684592$
$\qquad b: -1.9808 - (24 * 0.718 + 4 * (-1.9808) - 10) * 0.01 = -1.97389$
$\qquad E: (2 - (0.718 * 4 + (-1.9808)))^2 + (3 - (0.718 * 8 + (-1.9808)))^2 = 1.812$
…まだまだぜんぜんですね。
500回目
$\qquad a: 0.313962 - (160 * 0.313962 + 24 * 0.574629 - 64) * 0.01 = 0.313712$
$\qquad b: -1.9808 - (24 * 0.313962 + 4 * 0.574629 - 10) * 0.01 = 0.576293$
$\qquad E: (2 - (0.313962 * 4 + 0.574629))^2 + (3 - (0.313962 * 8 + 0.574629))^2 = 0.0362$
501回目
$\qquad a: 0.313962 - (160 * 0.313962 + 24 * 0.574629 - 64) * 0.01 = 0.313712$
$\qquad b: -1.9808 - (24 * 0.313962 + 4 * 0.574629 - 10) * 0.01 = 0.576293$
$\qquad E: (2 - (0.313962 * 4 + 0.574629))^2 + (3 - (0.313962 * 8 + 0.574629))^2 = 0.0359$
…徐々に近づいていってますがまだまだですね。
1500回目
$\qquad a: 0.251270 - (160 * 0.251270 + 24 * 0.991555 - 64) * 0.01 = 0.251265$
$\qquad b: 0.991555 - (24 * 0.251270 + 4 * 0.991555 - 10) * 0.01 = 0.991588$
$\qquad E: (2 - (0.251270 * 4 + 0.991555))^2 + (3 - (0.251270 * 8 + 0.991555))^2 = 1.42E-05$
1501回目
$\qquad a: 0.251265 - (160 * 0.251265 + 24 * 0.991588 - 64) * 0.01 = 0.251260$
$\qquad b: 0.991588 - (24 * 0.251265 + 4 * 0.991588 - 10) * 0.01 = 0.991621$
$\qquad E: (2 - (0.251265 * 4 + 0.991588))^2 + (3 - (0.251265 * 8 + 0.991588))^2 = 1.40E-05$
このくらいになるともうほぼ $a = 0.25$, $b = 1$ って感じですね!誤差関数($E$)の値も限りなくゼロに近い値になっています。
ということで、ちゃんと正しい値に向かって更新されていっていることがわかりました。これでひと安心です!
いちおうこちらも動画を載せておきましょう。こんな感じで推移していきます。
更新式は手に入ったけど…もうひと頑張り
さて、更新式も手に入ったし、どうやら正しいことも確認できたのですが、ここでもうひと頑張りしてみます。
誤差関数の式 $E$ は
(1-13)より
$\qquad E = \sum(y_i - f(x_i))^2$
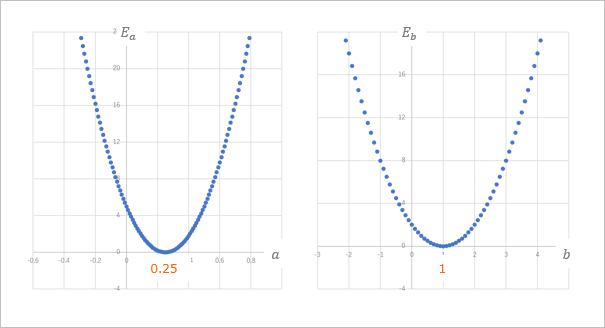
で、これを $a$ や $b$ を仮に固定したグラフで表すとこんな感じでした。
左側が $E_a$ のグラフで、右側が $E_b$ のグラフですね。
仮にこれを $\frac{1}{2}$ にして
(1 -49)$\qquad E = \frac{1}{2}(\sum(y_i - f(x_i))^2)$
としてグラフを書くと
こんな感じになります。
どちらのグラフも $E$ が最小となる点の値は同じですね。両方とも $a$ が $0.25$ で $b$ が $1$ というのは変わりません。
というわけで、ちょっと大人の事情でいままでの誤差関数の式を(1-49)のようにしてみちゃいましょう。
そうすると、、
$\qquad E = \frac{1}{2}(\sum(y_i - f(x_i))^2)$
$\qquad\quad = \frac{1}{2}((y_1 - f(x_1))^2 + (y_2 - f(x_2))^2)$
となって、
$\qquad E_1 = (y_1 - f(x_1))^2$
$\qquad E_2 = (y_2 - f(x_2))^2$
とすると、
$\qquad E = \frac{1}{2}(E_1 + E_2)$
と表せるので、
$\qquad \frac{\partial E}{\partial a} = \frac{1}{2}(\frac{\partial E_1}{\partial a} + \frac{\partial E_2}{\partial a})$
そして、
(1-35)より
$\qquad \frac{\partial E_1}{\partial a} = 2 * x_1((ax_1 + b) - y_1)$
(1-36)より
$\qquad \frac{\partial E_2}{\partial a} = 2 * x_2((ax_2 + b) - y_2)$
なので、
(1-37)より
(1-50)
\begin{align}
\frac{\partial E}{\partial a} &= \frac{1}{2}(\frac{\partial E_1}{\partial a} + \frac{\partial E_2}{\partial a}) \\
\\
&= \frac{1}{2}(2 * x_1((ax_1 + b) - y_1) + (2 * x_2((ax_2 + b) - y_2)) \\
\\
&= ((ax_1 + b) - y_1) * x_1 + ((ax_2 + b) - y_2) * x_2 \\
\\
&= \sum((ax_i + b) - y_i) * x_i
\end{align}
となって、$\sum$ の前の $2$ が取れました。
同様に、
(1-40)より
(1-51)
\begin{align}
\frac{\partial E}{\partial b} &= 1/2(\frac{\partial E_1}{\partial b} + \frac{\partial E_2}{\partial b}) \\
\\
&= \frac{1}{2}(2((ax_1 + b) - y_1) + 2((ax_2 + b) - y_2)) \\
\\
&= \sum((ax_i + b) - y_i)
\end{align}
こちらも $\sum$ の前の $2$ が取れました。
二乗和誤差は次数が $2$ だから微分すると係数で $2$ がでてくるから、あらかじめ $\frac{1}{2}$ しておけばいいよね。って発想ですね。まぁ、同じ結果が得られるならわざわざ $2$ 倍してなくてもいいんじゃない?ってところですかね。
まとめると
ということで、まとめると
(適当に決めた)パラメータと正しいパラメータの誤差を計るのには「誤差関数」を立てて、それは今回、
(1-52)$\qquad E = \frac{1}{2}\sum(y_i - f(x_i))^2$
という式で表すことにしました。二乗和誤差の式ですね。
で、実際にパラメータを更新する式は、
(1-53)$\qquad$ 更新後の $a$ = 更新前の $a$ - ($\sum$((更新前の $a$ * $x_i$ + $b$) - $y_i$) * $x_i$) * 調整値
(1-54)$\qquad$ 更新後の $b$ = 更新前の $b$ - ($\sum$((更新前の $b$ * $x_i$ + $b$) - $y_i$) * 調整値
で計算することができることがわかりました。
($\sum$ の前の $2$ がなくなっています。)
そしてなじみのある表記にすると…
今回は説明のため、$y = ax + b$ で話を進めてきましたが、機械学習の本やWebサイトなどでは別の文字で表すことが多いですよね。
というわけで、最後になじみのある表記との対応表を載せておきます。
| 今回使った記号 | 意味 | 機械学習の本などで使われる記号 |
|---|---|---|
| $a$ | 重み | $w$ とか $w_1$ |
| $b$ | バイアス | $b$ とか $w_0$ |
| 調整値 | 学習率 | $\eta$ など |
| $x$ | 入力値 | $x$ |
| $y$ | 出力値 | $y$ |
| $\hat y$ | 推測値 | $\hat y$ |
| $E$ | 誤差関数 (損失関数) |
$E$ |
なので、今回求める直線の式は
y = ax + b
と表してきましたが、これは
y = wx + b
もしくは
y = w_0 + w_1x
と表されていることが多いですね。
誤差関数は今回は二乗和誤差を利用したので、
\begin{align}
E &= \frac{1}{2}\sum(y_i - \hat y_i)^2 \\
\\
&= \frac{1}{2}\sum(y_i - f(x_i))^2 \\
\\
&= \frac{1}{2}\sum(y_i - (wx_i+ b))^2 \\
\\
もしくは \\
&= \frac{1}{2}\sum(y_i - (w_0 + w_1x_i))^2
\end{align}
重みの更新式は
\begin{align}
w &:= w - \eta(\frac{\partial E}{\partial w}) \\
\\
&:= w - \eta(\sum(\hat y_i - y_i) * x_i)) \\
\\
&:= w - \eta(\sum((wx_i + b) - y_i) * x_i) \\
\\
もしくは \\
w_1 &:= w_1 - \eta(\sum((w_0 + w_1x_i) - y_i) * x_i) \\
\\
&(※ ただし、\eta \quad は学習率)
\end{align}
バイアスの更新式は
\begin{align}
b &:= b - \eta(\frac{\partial E}{\partial b}) \\
\\
&:= b - \eta(\sum(\hat y_i - y_i)) \\
\\
&:= b - \eta(\sum(wx_i + b) - y_i) \\
\\
もしくは \\
w_0 &:= w_0 - \eta(\sum(w_0 + w_1x_1) - y_i) \\
\\
&(※ ただし、\eta \quad は学習率)
\end{align}
というようになります。
なお、初めに $a$ と $b$ の値を適当に 0$.75$ と $-2$にしましたが、これは初期値として通常はランダムで決められます。なので、どのような値からスタートするかはわかりません。
ふぅ。。長かったぁ。。
さいごに
さて、今回求めようとしていた $f(x) = y = ax + b$ は入力が一つで出力も一つなので、図にするとこんな感じでした。

左側の入力 $x$ を $f(x)$ で処理して、出力として $y$ を求めるってイメージです。
下の図はそれぞれのデータの処理を表しています。
このモデルの(限りなく)正しい $f(x)$ (のパラメータ)を求めるために勾配降下法を使って、少しずつ地道に誤差関数の最小値に到達するようにパラメータを調整していく過程をこの記事ではくどくどと説明してみました。
や、すごい冗長でしたよね。まぁ、でももしかしたら世界にあと一人くらいはこれくらいくどくどと説明しないとわかった感が得られない人もいるかもしれないので、そういう人に少しでも役立てばいいなぁと思って書きました。
ちょっと続き
今回は入力値1つに対して出力値1つのモデルで考えましたが、じゃあ、入力値が複数あるときはどうなるの?って疑問が当然出てくると思うので、そのあたりをちょっと続きで簡単に書いてみました。
勾配降下法(入力値が複数の場合の更新式)
--Excel VBA でニューラルネットワークをフルスクラッチしてみる--
あ、それから、以前書いていたExcel VBAでニューラルネットワークをフルスクラッチしてみる的な記事は以下のブログに移動しました。
無限不可能性ドライブ