たかしくんに時速10kmで日本全国を最短距離で走らせました

何日で達成できるでしょうか

最適化問題の勉強をしておりまして、思いついてしまった問題。
日本全国を最短距離で巡るのってどれぐらい時間がかかるのだろうか？
という疑問に答えるべく、pythonでちょっと計算してみました。

最適化問題をpythonでハンズオンすることが目的なので、問題設定の甘さはご容赦ください。
また、こちらの記事でも書きましたが、結局本命経路以外で円環経路を作ってしまう問題は解決できませんでした。
最適解ではなく近似解です、この辺りの解決法に詳しい方いらっしゃいましたらコメントお願いします！！

問題設定

算数の問題で良く出る（本当かは知らん）みんな大好きたかしくんを今回は使います。

たかしくんスペック

・たかしくんは強いので海を渡れます。
・たかしくんは強いので山があろうが谷があろうが一定の速度で走れます。
・たかしくんは強いので24時間走れます。

設定

・たかしくんは知的好奇心が旺盛なので日本全国を時速10kmで巡ろうと考えました。
・「日本全国」を今回は「全都道府県庁県庁所在地」と定義します
・たかしくんはせっかちなので移動は全て直線で行うものとします。

やってみた

都道府県庁所在地データの取得

都道府県庁所在地の経度と緯度はこちらの記事から引用しました。
Excelをダウンロード後、所在地名・経度・緯度のデータだけに成形します。

import pandas as pd
import numpy as np
df = pd.read_excel("city_list.xlsx")
display(df)

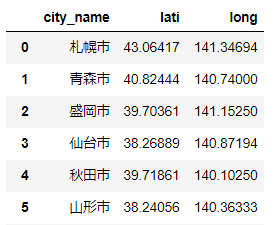
データはこんな感じ。latiが緯度(latitude)、longが経度(longitude)になります。

各所在地間の距離計算

47か所の所在地のお互いの距離計算をします。
本来であれば、例えば「沖縄-北海道なんて移動しないだろう」と考え組み合わせを絞るのが良い気もします。
今回はその選抜作業が面倒くさかったのと、何かミラクルが起きるかもという淡い期待からすべての組み合わせを網羅して計算しました。

経度・緯度を利用した距離計算はこちらの記事を流用しました。
二点の経度と緯度を引数(それぞれリスト型であることに注意！)として、その間の距離をkmで返す関数です。

def cal_rho(lon_a,lat_a,lon_b,lat_b):
    ra=6378.140  # equatorial radius (km)
    rb=6356.755  # polar radius (km)
    F=(ra-rb)/ra # flattening of the earth
    rad_lat_a=np.radians(lat_a)
    rad_lon_a=np.radians(lon_a)
    rad_lat_b=np.radians(lat_b)
    rad_lon_b=np.radians(lon_b)
    pa=np.arctan(rb/ra*np.tan(rad_lat_a))
    pb=np.arctan(rb/ra*np.tan(rad_lat_b))
    xx=np.arccos(np.sin(pa)*np.sin(pb)+np.cos(pa)*np.cos(pb)*np.cos(rad_lon_a-rad_lon_b))
    c1=(np.sin(xx)-xx)*(np.sin(pa)+np.sin(pb))**2/np.cos(xx/2)**2
    c2=(np.sin(xx)+xx)*(np.sin(pa)-np.sin(pb))**2/np.sin(xx/2)**2
    dr=F/8*(c1-c2)
    rho=ra*(xx+dr)
    return rho

あとはこの関数に全組み合わせをぶち込んでいきます。

#引数となるリストの入れ物を用意
loc_A = []
lon_A = []
lat_A = []

loc_B = []
lon_B = []
lat_B = []

#ひたすらぶち込む
for i in range(47):
    for j in range(47):
        loc_A.append(i)
        lon_A.append(df["long"][i])
        lat_A.append(df["lati"][i])

        loc_B.append(j)
        lon_B.append(df["long"][j])
        lat_B.append(df["lati"][j])

#計算！
rho=cal_rho(lon_A,lat_A,lon_B,lat_B)

#結果をデータフレームに
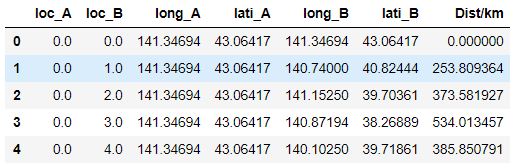
combi_df = pd.DataFrame([loc_A,loc_B,lon_A,lat_A,lon_B,lat_B,rho]).T
combi_df.columns = ["loc_A","loc_B","long_A","lati_A","long_B","lati_B","Dist/km"]
combi_df = combi_df.fillna(0)
combi_df.head(5)

結果、各地点間の距離を計算することができました。

最短経路の計算

ここについては前回の記事やおおもとの記事とほとんど同じ実装になっていますが、matplotlibによる描画の大きさだけ変えています(参考記事)
図の描画の関数がこちら。

import random, numpy as np, pandas as pd, networkx as nx, matplotlib.pyplot as plt
from itertools import chain, combinations
from pulp import *

def draw(g):
    plt.figure(dpi=150)
    rn = g.nodes() # ノードリスト
    pos = nx.spring_layout(g) # ノード位置
    """描画"""
    nx.draw_networkx_labels(g, pos=pos)
    nx.draw_networkx_nodes(g, node_color='w', pos=pos)
    nx.draw_networkx_edges(g, pos=pos)
    plt.show()

最適化計算のコードはこちら。
Networkxについてはこちらの記事が読みやすいです！
今回は取りうる値を0,1にした離散最適化問題として解きました(参考記事)。

#47地点を定義
n = 47 # ノード数
g = nx.random_graphs.fast_gnp_random_graph(n, 1, 8)

#47地点間の距離をインプット
for a,b in g.edges():
    col_idx = a * 47 + b
    g.edges[a, b]["dist"] = combi_df.loc[col_idx,"Dist/km"]

#いざ計算
source, sink = 0, 46 # 始点, 終点
r = list(enumerate(g.edges()))
m = LpProblem() # 数理モデル
x = [LpVariable('x%d'%k, lowBound=0, upBound=1,cat="Integer" ) for k, (i, j) in r] # 変数(路に入るかどうか)
m += lpSum(x[k] * g.edges[i,j]["dist"] for k, (i, j) in r) # 目的関数
for nd in g.nodes():
    m += lpSum(x[k] for k, (i, j) in r if i == nd) \
        + lpSum(x[k] for k, (i, j) in r if j == nd) == {source:1, sink:1}.get(nd, 2) # 制約
m.solve()

print([(i, j) for k, (i, j) in r if value(x[k]) == 1])
print(LpStatus[m.status])
print(value(m.objective))

一つ目のprintは経路の表示、二つ目は最適化計算がうまくいったか、三つめは最適解の表示です。
出力結果はこちら。

optimalとなっているので最適解が叩き出せたみたい！！
そして最短経路は4304km！！
なのでたかしくんは430時間、つまり約17日22時間で日本全国を巡れるらしい！

やったーーー！計算できた！！！
と思っていたのもつかの間でした。

円環経路問題

どんな経路を巡ったのだろうか？と思い、描画をしてみました。
最適化結果の確認用のコードはこちら。

G = nx.Graph()
for k,(i,j) in r:
    if value(x[k]) ==1:
        nx.add_path(G, [i, j])
draw(G)

描画結果がこちら。
前回の記事でも取り上げた円環生成問題が生じていました。
これは、「ある地点に着目した時に、経由点では2本の道、始点終点では1本の道が伸びている」という制約条件の甘さから生じる問題です。

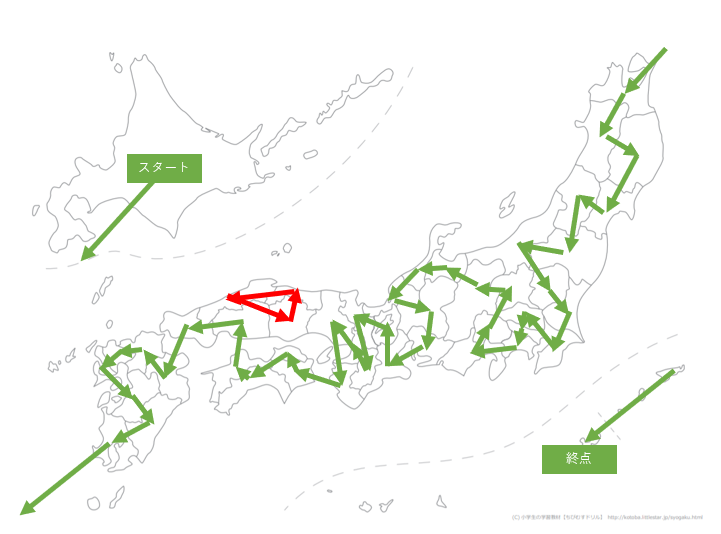
こちらのサイトから白地図を拝借しプロットしてみました。
東北・関東・中国地方でぐるぐる回ってる場所がありますね。

ここからは経路を少しいじくって、一本の経路にしていこうと思います。
恣意的な操作が加わりますので最適解になるのかが分からなくなりますが、おおよそ近いだろうと踏んで考えてみます。

秋田-新潟間を切る

切りたい経路の長さをとてつもなく長くしてみます。
こんな感じです。

pair_list = [(4,14),(14,4)]
for a,b in pair_list:
    col_idx = a * 47 + b
    combi_df.loc[col_idx,"Dist/km"] = 1000000

これで最適化計算をしてみます。
結果は地図だけ示しますね。
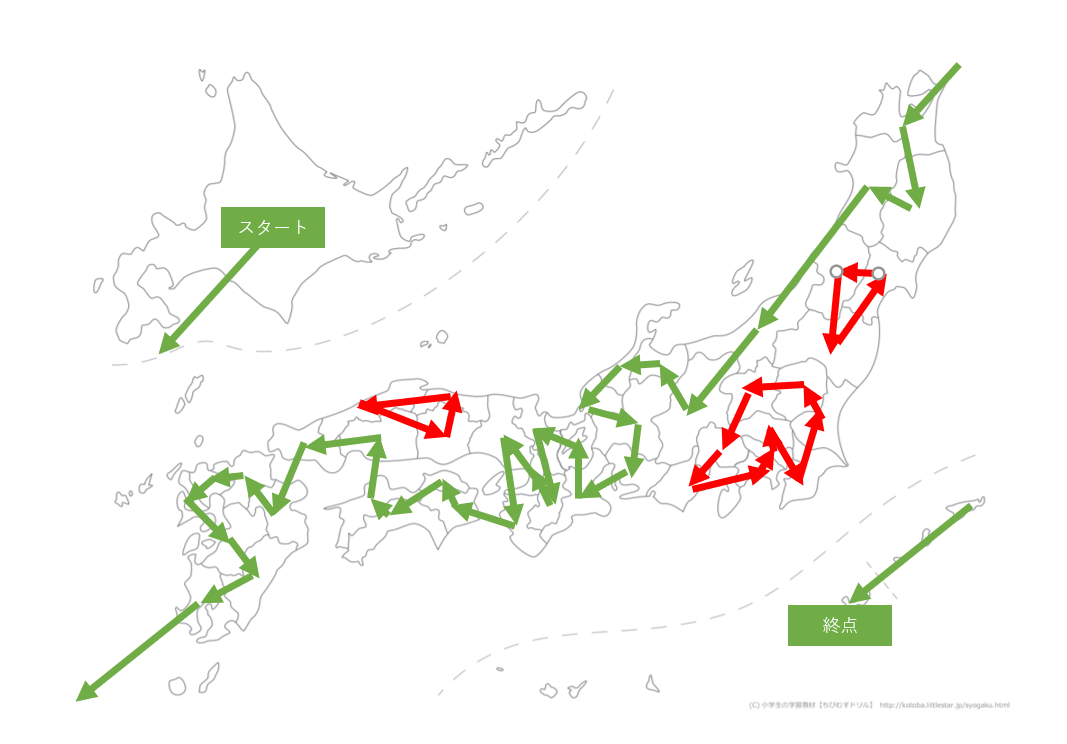
東北地方の統合に成功しました！！やったぜ。
この場合でも4309kmぐらいなので、経路一つだけの変更ではそこまで影響がなさそうですね。

新潟-長野間を切る

関東地方の統合をどうするか悩みました。
そこで、新潟から長野に行かずに群馬へ行き、関東の円環に合流した後に長野へいく、というルートを考えてみました。
なので新潟-長野間の経路を切ってみました。

その結果がこちら。

新潟から栃木へ行き、うまく統合することができました。
距離はやや伸びてしまいましたが4326kmとなりました。

島根-岡山間を切る

最後、中国地方の統合をどうするか。
島根-岡山間の移動が見られますが、岡山-島根を移動するのであれば鳥取か広島を経由するのが良さそう。
なので島根-岡山間を切ってみます。

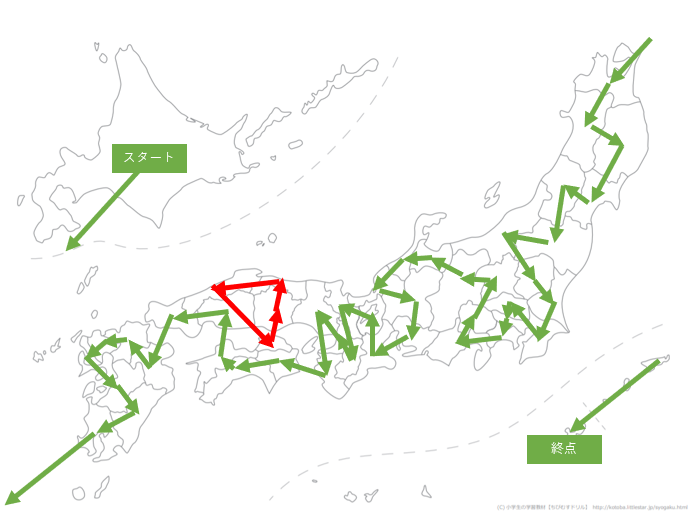
香川を巻き込みやがった・・・
どれだけそこでこじんまりしたいんだよ。

島根-香川間を切る

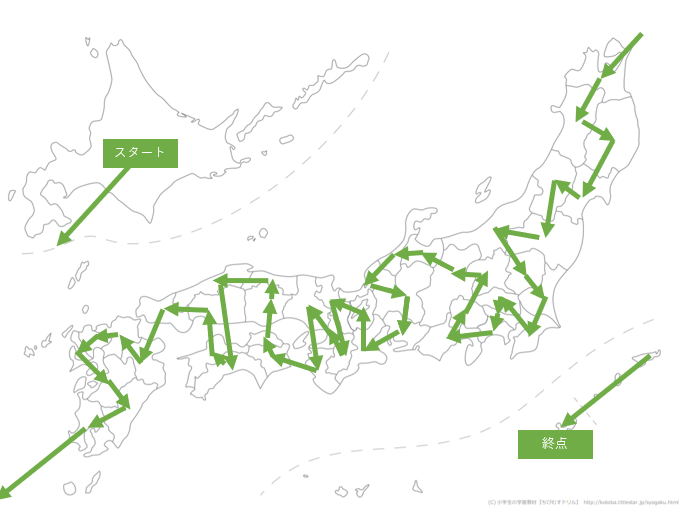
ということで島根-香川間を切ってみます。
その結果がこちら！
島根から高知へワープしているものの、ついに一本になりました！！
距離は4361kmに。

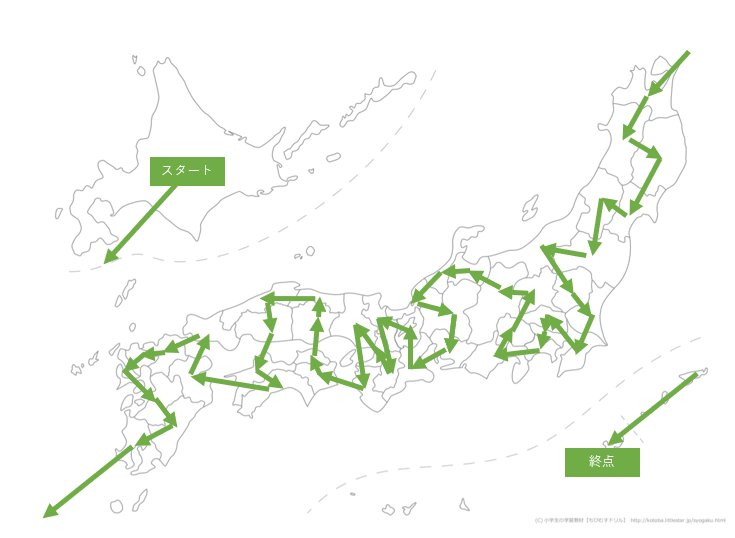
ちょっと島根-高知間のワープが気になったのでここもぶち切ってみました。
今度は高知から大分へワープして、山口は九州に行ってから拾いに行くようです。
距離も4361kmと同じぐらいになりました。
中国・四国周りは一筆書きするのが難しそうですね。

結論

走る距離：だいたい4361km
走る時間：だいたい18日4時間

さいごに

最適化問題面白い！
これからもいろいろ実験してみようと思います。
最後まで読んでいただきありがとうございます、LGTMしていただけると励みになります！