前回の続き
前回の記事ではいくつかの点をとったときに、始点から終点までの最短経路を求めるコードを読み解きました。
前回のコードでは全ての点を経由することができなかったので、その部分を少し考えてみます。
結局色々失敗してる最適化のお勉強メモですのでご了承ください。
色々まとまっている教科書はこちら。
実装内容
前回の実装
ある点に注目した時に、その点に入る道とその点から出る道の本数の関係を定式化しました。
始点の場合はその点から出る道のほうが一本多く、終点の場合はその点に入る道の方が一本多い、
それ以外については双方が同数になるという実装です。
この実装だと「全ての点を通った」最短経路にはならないので、その部分をトライしてみます。
for nd in g.nodes():
m += lpSum(x[k] for k, (i, j) in r if i == nd) \
== lpSum(x[k] for k, (i, j) in r if j == nd) + {source:1, sink:-1}.get(nd, 0) # 制約
進歩1:ある点に出入りする本数を規定する
ある点に注目した時に、その点に入る本数と出る本数の合計が2(終点始点は1)になるようにすれば、「通らない」ということは無くなりそう。
ですが実際にやってみると、本命の経路以外で輪を作ってしまうパターンに。
難しい・・・。
from pulp import *
import networkx as nx
g = nx.fast_gnp_random_graph(10, 0.8, 0) #第三引数を1にすると双方向の経路をg.edgesに保持
source, sink = 0, 2 # 始点, 終点
r = list(enumerate(g.edges()))
m = LpProblem() # 数理モデル
x = [LpVariable('x%d'%k, lowBound=0, upBound=1) for k, (i, j) in r] # 変数(路に入るかどうか)
m += lpSum(x) # 目的関数
for nd in g.nodes():
m += lpSum(x[k] for k, (i, j) in r if i == nd) \
+ lpSum(x[k] for k, (i, j) in r if j == nd) == {source:1, sink:1}.get(nd, 2) # 制約
m.solve()
print([(i, j) for k, (i, j) in r if value(x[k]) ==1])
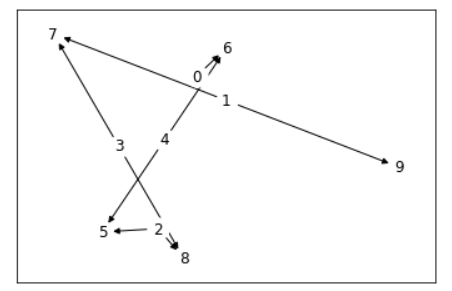
この結果がこちら。
0から2へ行く、というはずなのに、0,5,2以外の点で円環ができてしまっています。
この2つの経路をどうつないだらいいのか・・・。
進歩2:道に距離の概念を導入
前回の実装ではすべての道を同じ長さと考えて最短経路を選択していました。
もう少し実用に近づけるべく、長さの概念を入れてみるとどうなるかやってみました。
一旦長さは「各経路の両端のノード番号を足した値」と定義してみました。
g.edges[i,j]["dist"]のようなお作法についてはこちらの記事を参考にしました。
# https://qiita.com/kzm4269/items/081ff2fdb8a6b0a6112f
n = 10 # ノード数
g = nx.random_graphs.fast_gnp_random_graph(n, 0.9, 8)
for i,j in g.edges():
g.edges[i, j]["dist"] = i+j
最適化部分のコードはたいして変更していませんが念のため再掲です。
source, sink = 0, 9 # 始点, 終点
r = list(enumerate(g.edges()))
m = LpProblem() # 数理モデル
x = [LpVariable('x%d'%k, lowBound=0, upBound=1) for k, (i, j) in r] # 変数(路に入るかどうか)
m += lpSum(x[k] * g.edges[i,j]["dist"] for k, (i, j) in r) # 目的関数
for nd in g.nodes():
m += lpSum(x[k] for k, (i, j) in r if i == nd) \
+ lpSum(x[k] for k, (i, j) in r if j == nd) == {source:1, sink:1}.get(nd, 2) # 制約
m.solve()
print([(i, j) for k, (i, j) in r if value(x[k]) ==1])
最適な経路に選ばれたものを取り出して図示します。
sprint_layoutについてはこちらの記事が便利でした。
def draw(g):
rn = g.nodes() # ノードリスト
pos = nx.spring_layout(g, pos={i:(i/4, i%4) for i in rn}) # ノード位置
"""描画"""
nx.draw_networkx_labels(g, pos=pos)
nx.draw_networkx_nodes(g, node_color='w', pos=pos)
nx.draw_networkx_edges(g, pos=pos)
plt.show()
G = nx.DiGraph()
for k,(i,j) in r:
if value(x[k]) == 1:
nx.add_path(G, [i, j])
draw(G)
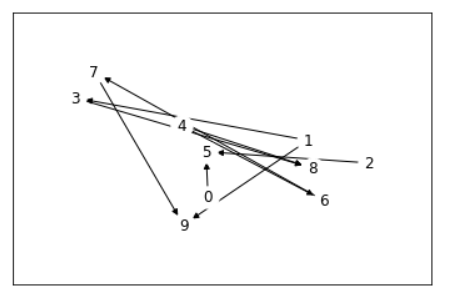
描画の結果はこちら。
今回はたまたまちゃんとした経路になったようです。
円環を作ってしまう現象はこちらでも起こりうる状態なはず。
最適解の時の総距離はこちら。
これもあってそう!
value(m.objective)
>>>81.0
最後に
最適化楽しい!