0.グラフの描画ってどうやるの?
二次元に描画するためには各頂点に適切に座標を与える必要がありますが、グラフは頂点と辺の情報しか持っていません。どのように頂点を配置すればよいのでしょう??
この記事ではグラフをいい感じに配置するアルゴリズム Fruchterman-Reingold algorithm を説明します。Pythonだと networkxというライブラリで簡単に使用できます。しかし簡単すぎて悔しいので networkxの GitHub の実装を追いながら仕組みを確認していきます。
この記事の流れはこうです。
- 動かしてみる
- アルゴリズムの説明
- Networkx の実装を追う
1.動かしてみる
動けば満足な方のために先に実装例を示しときます。Google colaboratory だと既にnetworkxがインストールされてるので、コピペですぐ試せます。
ランダムに配置 → random_layout()
import networkx as nx
import matplotlib.pyplot as plt
N = 500 # 頂点数
K = 5
P = 0.05
G = nx.watts_strogatz_graph(N,K,P) # 適当なグラフ
pos = nx.random_layout(G, seed=0)
# グラフを描画
plt.figure(figsize=(15,15))
nx.draw_networkx(G, pos, with_labels=False, node_shape='.')
plt.axis("off")
plt.show()

うわぁ…。見たくない…。
ランダムな配置では見るに堪えませんね。
いい感じに配置 → spring_layout()
import networkx as nx
import matplotlib.pyplot as plt
N = 500 # 頂点数
K = 5
P = 0.05
G = nx.watts_strogatz_graph(N,K,P)
pos = nx.spring_layout(G)
# グラフを描画
plt.figure(figsize=(15,15))
nx.draw_networkx(G, pos, with_labels=False, node_shape='.')
plt.axis("off")
plt.show()
いい感じに配置されてますね。
「いい感じの配置」ってなに?
もう少し厳密に「よい配置」を考えます。例えば今、グラフ$G$の情報を以下のように持っているとします。
$G = (V, E)$
$V$:頂点集合
$E$:辺集合
このグラフを二次元に配置する方法は無数にあります。(先ほどのようにランダムに配置してもいいわけです。)しかしできることなら見やすく配置したいです。以下の条件を満たす配置を「よい配置」としましょう。
①辺の接続関係が距離に反映されている
つまり辺で接続された点どうしは近くに配置して、辺で接続されていない点どうしは遠くに配置するようにします。隣接行列だと、接続されていない部分はinfにしたりするので、辺の有無に関係なくすべての点を同様に扱えそうです。
➁頂点が重ならない
頂点どうしが重なっていては、辺も見れないので困りますね。
以上二つの条件を満たすようなグラフ配置を求めたいです。それを実現するのが、**力学モデル(力指向グラフ)**です。
そして先ほどのnetworkx.spring_layout()では Fruchterman-Reingold algorithm が使われています。今回はこれを紹介します。この手法のイメージをつかむために以下のgifを見てください。

ランダムな初期配置から、だんだんきれいになっていく!!(こちらから借りました)
アルゴリズムを知りたくなってきましたか?(y/n)
y
知りましょう。
2.Fruchterman-Reingold algorithm
力を定義
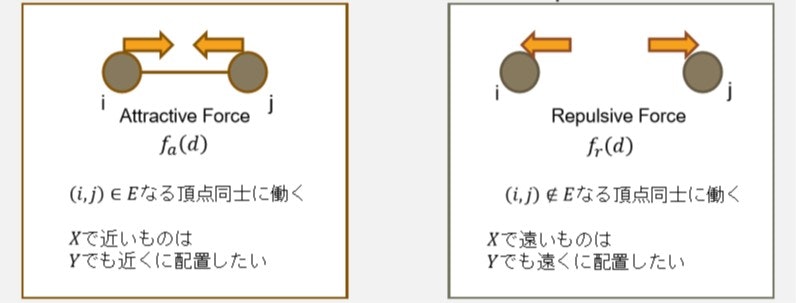
力学モデルでは、頂点に力を加えて移動させていきます。Fruchterman-Reingold algorithm では、**引力(Attractive Force)と斥力(Repulsive Force)**が出てきます。
引力は辺で接続されている頂点どうしに働きます。一方斥力は辺で接続されていない頂点どうしに働きます。これは先ほどの条件①「辺の接続関係が距離に反映されている」に対応しています。
力はどのように定義してもいいのですが、とりあえず論文で提案されている定義を使ってみましょう。
引力:$f_a = \dfrac{d^2}{k}$
斥力:$f_r = -\dfrac{k^2}{d}$
$d$:頂点間の距離
$k = C \sqrt{\dfrac{\text{area}}{|V|}}$, $C \in \mathbb{R} ,\ \ \text{area}$は描画する画面の面積
ばねの式みたいで直観的ですね。力と距離の関係のグラフは以下です。
- 引力は遠くにあるほど強く働く
- 斥力は近くにあるほど強く働く
- 引力と斥力はある距離 $k$ で等しくなる
力が拮抗する距離 $k$ を適切な大きさにすれば、先ほどの条件➁「頂点が重ならない」を満たすことができます。
アルゴリズム
さてアルゴリズムを見てみましょう。
- ランダムに初期配置する
- 各頂点について、引力と斥力を計算
- 力に従って頂点を移動。ただし枠の外に出ないようにする。
- 温度 $t$ を下げる
- 2~4 を一定回数くりかえす
見慣れない変数 $t$ が出てきました。温度 $t$ は頂点の移動量を制限するパラメータです。つまりステップ2において計算した移動方向ベクトル( $v$ とおく)に対して、移動量を $t$ 以下になるようにします。
$v = \dfrac{v}{| v|} * \min(| v|, t)$
この温度$t$を適切に小さくしていきます。するとはじめは移動量が大きいものの、終盤はあまり移動しないようになります。(収束性を保証)
あと論文ではステップ3では画面内に配置するために壁との衝突を弾性反射として扱ったりしています。このあたりを詳しく知りたい方はもとの論文"Graph drawing by force‐directed placement"を読んでください。(networkxの実装では考慮していません…)
~~ここまででアルゴリズムがわかったので、実装してみます。~~ ↑ めんどくさくなったので実装は読者に委ねます。
この記事では車輪の再発明をせずに networkx の実装方法を見ていきます。
3.Networkx の実装を見てみる
人の実装を見て学ぼう。ただし NetworkX 2.4 当時のもので、例外処理など説明しない部分は省略しました。
記事の初めのほうで networkx.spring_layout()を使用して「いい感じ」にグラフを描画しました。GitHubを見てみると、
spring_layout = fruchterman_reingold_layout
なんと参照しているだけ! 今度は参照先であるfruchterman_reingold_layoutを見てみます。
def fruchterman_reingold_layout(G,
k=None,
pos=None,
# 省略
seed=None):
"""長々したdocstring
"""
import numpy as np
G, center = _process_params(G, center, dim)
"""
いろいろ初期化してる部分(省略)
"""
"""
ここから下が大切
"""
try:
# Sparse matrix
if len(G) < 500: # sparse solver for large graphs
raise ValueError
A = nx.to_scipy_sparse_matrix(G, weight=weight, dtype='f')
if k is None and fixed is not None:
# We must adjust k by domain size for layouts not near 1x1
nnodes, _ = A.shape
k = dom_size / np.sqrt(nnodes)
pos = _sparse_fruchterman_reingold(A, k, pos_arr, fixed,
iterations, threshold,
dim, seed)
except ValueError:
A = nx.to_numpy_array(G, weight=weight)
if k is None and fixed is not None:
# We must adjust k by domain size for layouts not near 1x1
nnodes, _ = A.shape
k = dom_size / np.sqrt(nnodes)
pos = _fruchterman_reingold(A, k, pos_arr, fixed, iterations,
threshold, dim, seed)
if fixed is None and scale is not None:
pos = rescale_layout(pos, scale=scale) + center
pos = dict(zip(G, pos))
return pos
try-except部分では、グラフの大きさによって呼び出す関数を分けています。(if文じゃダメなんですかね…?教えてください。)
- $頂点数 < 500$なら、
_fruchterman_reingold()を呼び出す - $頂点数 \geq 500$なら、
_sparse_fruchterman_reingold()を呼び出す
**頂点数が多い場合は、sparse solverを使っているみたいです。**ここまで見てもアルゴリズムの部分にたどり着けてないので、_fruchterman_reingold()を見てみましょう。
def _fruchterman_reingold(A, k=None, pos=None, fixed=None,
iterations=50, threshold=1e-4, dim=2,
seed=None):
# Position nodes in adjacency matrix A using Fruchterman-Reingold
# Entry point for NetworkX graph is fruchterman_reingold_layout()
# Sparse version
import numpy as np
if pos is None:
# random initial positions
pos = np.asarray(seed.rand(nnodes, dim), dtype=A.dtype)
else:
# make sure positions are of same type as matrix
pos = pos.astype(A.dtype)
# optimal distance between nodes
if k is None:
k = np.sqrt(1.0 / nnodes)
# the initial "temperature" is about .1 of domain area (=1x1)
# this is the largest step allowed in the dynamics.
t = max(max(pos.T[0]) - min(pos.T[0]), max(pos.T[1]) - min(pos.T[1])) * 0.1
# simple cooling scheme.
# linearly step down by dt on each iteration so last iteration is size dt.
dt = t / float(iterations + 1)
displacement = np.zeros((dim, nnodes))
for iteration in range(iterations):
displacement *= 0
# loop over rows
for i in range(A.shape[0]):
if i in fixed:
continue
# difference between this row's node position and all others
delta = (pos[i] - pos).T
# distance between points
distance = np.sqrt((delta**2).sum(axis=0))
# enforce minimum distance of 0.01
distance = np.where(distance < 0.01, 0.01, distance)
# the adjacency matrix row
Ai = np.asarray(A.getrowview(i).toarray())
# displacement "force"
displacement[:, i] +=\
(delta * (k * k / distance**2 - Ai * distance / k)).sum(axis=1)
# update positions
length = np.sqrt((displacement**2).sum(axis=0))
length = np.where(length < 0.01, 0.1, length)
delta_pos = (displacement * t / length).T
pos += delta_pos
# cool temperature
t -= dt
err = np.linalg.norm(delta_pos) / nnodes
if err < threshold:
break
return pos
ここがアルゴリズムの実装部分ですね。引力や斥力をどう扱っているのかまとめてみます。
- コード間の最適な距離: $k = \sqrt{\dfrac{1}{|V|}}$
- 点―点間の距離: $\text{distance} = \max(\text{distance}, 0.01)$
- 点―点の隣接行列の値:$A_i$
- 温度 $t$ :$\max(\text{初期配置の定義域の幅}, \text{初期配置の値域の幅})*0.01$
- 温度の下げ方 :
t -= dt、ただし $dt = \dfrac{t}{\text{iteration}+1}$ - 方向ベクトル:$\text{delta}$
- 引力: $f_a = \dfrac{k^2}{\text{distance}^2}$
- 斥力:$f_r = - A_i * \dfrac{\text{distance}}{k}$
最適な距離の式は論文に当てはめると、$C = 1, \text{area} = 1$となってます。単純!
温度 $t$ は最初は大きく下げるように、iterationが進むにつれて少しづつ下げるようになってます。
$\text{delta}$ は厳密には方向ベクトルではないですが、最終的にはノルムを調整してるのでそう書きました。
とても気になるのは力の定義です。**引力も斥力も論文のものとは違います。**論文が1991年のものなので、その後改良版が出たりしてるんですかね。また他の知見として重み付きのグラフの場合、斥力に隣接行列の値をかければ良いことも分かりました。
自分で実装してみる際は、同様の設定で実装すると良いと思います。
おまけ
ソースコードを少しいじって、アルゴリズムの動きを可視化してみました。(パラメータをいじって200回のイテレーションにしました。)

バラバラの点のかたまりが徐々にヒモのようになっていくのが興味深いですね。自分でほとんど実装せずに、参考にしたサイト「グラフ(ネットワーク)を奇麗に描画するアルゴリズム」と近いものが得られました。やったね。
まとめ
簡単にグラフを扱えるnetworkxの裏を少しでも覗こうと、グラフ描画アルゴリズムである Fruchterman-Reingold algorithm を説明しました。アルゴリズムを学んだら実装してみるのも大切ですが、強い人の実装を見るのも勉強になりますね。質問や指摘などお待ちしてます。
参考文献
グラフ(ネットワーク)を奇麗に描画するアルゴリズム
:ほんとうに優れた記事です!
Graph drawing by force‐directed placement, 1992
:Fruchterman と Reingold の論文
networkx GitHub
:今回少し解説したもの
力学モデル(wikipedia)
:他の手法も見てみたい
【Python】NetworkX 2.0の基礎的な使い方まとめ Qiita
:わかりやすい記事