ペンシルパズル「ペーパーチャレラン」をプログラミングで解いてみる その2

概要

　以前、「計算迷路チャレラン」というパズルを解いたという記事を紹介しました。
　　ペンシルパズル「ペーパーチャレラン」をプログラミングで解いてみる - Qiita
　ただ、この記事では、解き方の詳細までは記述していませんでした。
　今後の備忘録を兼ねて、それをまとめてみようと思います。

※下記に連ねる「枝刈り」などの高速化のコツは他のパズルにも応用が効くと思います
※代表的な高速化手段の一つであるビットボードについては、次の記事をご覧ください
(ペーパーチャレランでは結局使用しませんでした。使いどころがあれば、ご教示いただけると助かります)
　パズルゲー「ルームスイーパ」をC++で解いてみた その3 - Qiita
　ビットボードの凄さをざっくりと解説してみる - Qiita

2017/12/27追記：

　種々の枝刈りを取り込んだ、最新のプログラムのソースコードを配布します。
　　https://github.com/YSRKEN/challerunF

2017/12/26追記：

「枝刈りその4：見込みのない経路を途中で打ち切る」を実装したので取り急ぎ報告まで。

計算迷路チャレランとは？

　参考→http://www.challeran.jp/crland/pe-cha/paper-challeran/0705/setumei.html

• スタート地点から格子の辺を伝い、ゴール地点を目指します
• 格子の交点と交点を結ぶ辺の上に、「+3」や「×2」などの「演算」が書かれています
• (実際の問題では、演算子は+と-と×(*)の3種類、それにくっついた数字は1桁)
• スタート始点での持ち点は1点。辺を通過すると、そこに書いてある「演算」を持ち点に施します
• 同じ辺を二度通ることはできません。ただし、同じ交点を二度通っても構いません
• ゴール地点に着いた際、より持ち点が大きい方が勝ちです

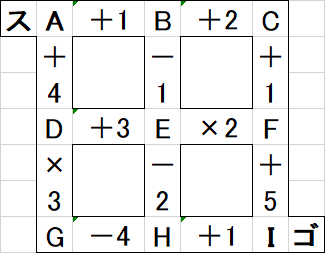
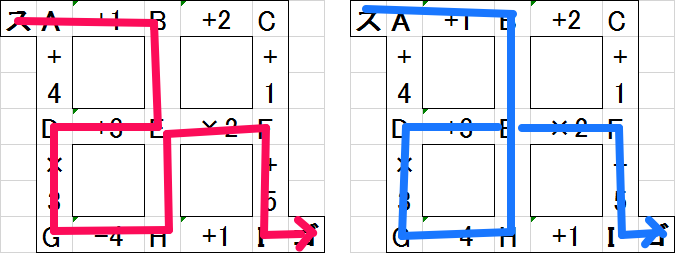
　例として、次のような問題があったとします。

　仮にス→Ａ→Ｄ→Ｇ→Ｈ→Ｉ→ゴと進むと、(1+4)×3-4+1＝12点となります。
　一方、ス→Ａ→Ｂ→Ｃ→Ｆ→Ｅ→Ｄ→Ｇ→Ｈ→Ｉ→ゴと進むと、((1+1+2+1)×2+3)×3-4+1＝36点となります。
　なるべく点数を増やしたいので、この場合は後者を採用すべきです(ちなみにこの問題の最適解は36点)。

　また、同じ交点を二度通っても構いませんので、ス→A→B→E→D→G→H→E→F→I→ゴと進んでも、ス→A→B→E→H→D→G→D→E→F→I→ゴと進んでも構いません。
　前述したように、演算は通った辺の順に適用されますので、交点の通り方が変われば点数も変化するのです。

問題の解き方について

　説明の前に、各種枝刈りがどの程度効くのかを、適当な問題を例に表として纏めました。
　枝刈り1の時点で計算時間が半減していますが、枝刈り2・枝刈り3でそれぞれ1割ほど改善していますし、枝刈り4に至っては最大で4倍近くも高速化されていることが分かります。
(Core i7-4790K,Windows 10 64bit,Visual Studio 2017,C++,1スレッド,数値の単位は[s])

問題サイズ	DFS	DFS+枝刈り1	DFS+枝刈り1～2	DFS+枝刈り1～3	DFS+枝刈り1～4
5x6	4.213	2.194	2.032	1.741	1.043
5x7	171.544	91.698	85.959	75.765	49.061
6x6	509.126	259.714	234.914	206.251	55.808

深さ優先探索(DFS)

「選択した経路を奥に奥に進む」といった、非常にシンプルな手法です。
　ただ、この問題特有のポイントもありますので、使用したアルゴリズムを擬似コードで示します。

void dfs(現在の交点の位置, 現在の得点, 現在の経路){
    // ゴールの交点に着いた際の処理
    if(現在の交点の位置 == ゴールの交点の位置){
        if(現在の得点 > 最高得点){
            最高の得点 = 現在の得点;
            最高の経路 = 現在の経路;
        }
    }
    // 交点から別の交点に進む
    for(各進行方向 : 全進行方向){
        // 既に通ったことのある辺を通過するルートは行けない
        if(各進行方向が既に通ったことのある辺である){
            continue;
        }
        // ある方向に進む
        次の交点の位置, 次の得点, 次の経路 = move(現在の交点の位置, 現在の得点, 現在の経路, 各進行方向);
        // 再帰を1段階進める
        dfs(次の交点の位置, 次の得点, 次の経路);
        // 進んだ方向から元に戻る
        現在の交点の位置, 現在の得点, 現在の経路 = back(次の交点の位置, 次の得点, 次の経路, 各進行方向);
    }
}

• 上記コードの「ゴールの交点」とは、例えば前述のサンプル問題で言うところのIマスを指します
• ゴールの交点に着いても探索が続くのは、ゴールの交点が角以外にあった際、 「一度ゴールの交点に行った後に、ぐるっと回って再びゴールの交点に着く」 といったことがありうるからです( 同じ交点を二度通っても構わない ことに注意)
• 既に通ったことのある辺は通過できないので、現実的には「辺に番号を振って通過の有無を管理する」といったことが必要になります。「現在の交点→次の交点の辺が『現在の経路』で通った辺に含まれるか」をチェックするのは高コストですので……

枝刈りその1：ゴールが角にあるか否か

　深さ優先探索で探索する系のプログラムにつきものなのが、計算量爆発にどう対処するかです。
　かの有名な動画『フカシギの数え方』より、同じ盤面規模でも遥かに探索量が多くなるこの問題では、少しでも計算量を削っておきたいところです。
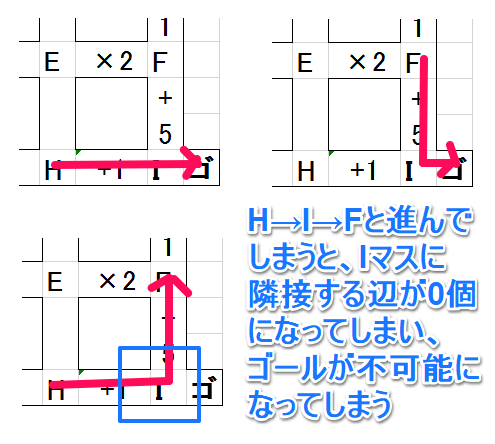
　そこでまず思いつくのが、「ゴールの交点が角にあるか否か」で再帰する関数を分ける方法です。

　上記画像のIマスが「ゴールの交点」だとします。すると、HマスからIマスに進んだ際、そこからFマスに進むことはもはや許されません。なぜなら、それをしてしまうと、もう 二度とIマス(ゴールの交点)に行けない からです。

　一方、「ゴールの交点」がHマスのような壁際や、Eマスのような宙ぶらりんの位置にあった場合、そのマスを通過したところで、再びゴールする可能性が存在します。
　ゆえに、「ゴールの交点が角にある」と始めから分かっている場合、次の擬似コードでも問題なく解を探すことができます。

void dfs(現在の交点の位置, 現在の得点, 現在の経路){
    // ゴールの交点に着いた際の処理
    if(現在の交点の位置 == ゴールの交点の位置){
        if(現在の得点 > 最高得点){
            最高の得点 = 現在の得点;
            最高の経路 = 現在の経路;
        }
        return;  // ★ここにreturn文が書けるのが重要！★
    }
    // 交点から別の交点に進む
    for(各進行方向 : 全進行方向){
        // 既に通ったことのある辺を通過するルートは行けない
        if(各進行方向が既に通ったことのある辺である){
            continue;
        }
        // ある方向に進む
        次の交点の位置, 次の得点, 次の経路 = move(現在の交点の位置, 現在の得点, 現在の経路, 各進行方向);
        // 再帰を1段階進める
        dfs(次の交点の位置, 次の得点, 次の経路);
        // 進んだ方向から元に戻る
        現在の交点の位置, 現在の得点, 現在の経路 = back(次の交点の位置, 次の得点, 次の経路, 各進行方向);
    }
}

枝刈りその2：入ったら出てこれる交点か

　それぞれの交点に注目してみましょう。「スタートの交点」「ゴールの交点」以外の交点では、
　　「交点に入った数＝交点から出た数」
となります。つまり、交点を通過する度に、その交点に隣接する「通過可能な辺」の数は2つづつ減っていきます。
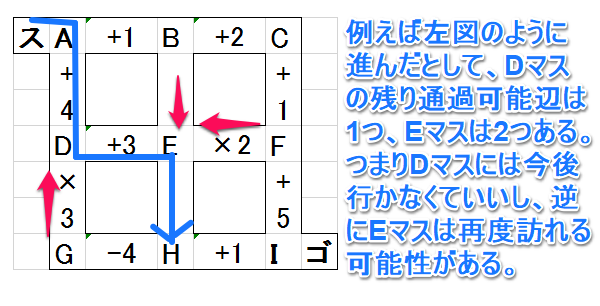
ゆえに、「通過可能な辺」が残り1つしかない交点は、それが「スタートの交点」「ゴールの交点」以外である場合、入ると出てこれない交点となります。要するに「探索時に進まなくてもいい交点」となるのです。

　このことを擬似コードで表現すると次のようになります。

// 通過可能辺の数を事前に初期化しておく
// ・ただし「ゴールの交点」は、実際の本数+1(例えば角なら2本ではなく3本と扱う)に
// 　しておかないと、ゴールに向かう方向も枝刈りしてしまうので注意！
init(各交点における通過可能な辺の数);

void dfs(現在の交点の位置, 現在の得点, 現在の経路){
    // ゴールの交点に着いた際の処理
    if(現在の交点の位置 == ゴールの交点の位置){
        (中略)
    }
    // 交点から別の交点に進む
    --各交点における通過可能な辺の数[現在の交点の位置]; //★変更ポイント★
    for(各進行方向 : 全進行方向){
        // 既に通ったことのある辺を通過するルートは行けない
        if(各進行方向が既に通ったことのある辺である){
            continue;
        }
        // 次の交点に行けるかを判定する
        次の交点の位置 = move'(現在の交点の位置, 各進行方向);    //★変更ポイント★
        if(各交点における通過可能な辺の数[次の交点の位置] <= 1){ //★変更ポイント★
            continue;                                        //★変更ポイント★
        }                                                    //★変更ポイント★
        // ある方向に進む
        --各交点における通過可能な辺の数[現在の交点の位置]; //★変更ポイント★
        次の得点, 次の経路 = move(現在の交点の位置, 現在の得点, 現在の経路, 各進行方向);
        // 再帰を1段階進める
        dfs(次の交点の位置, 次の得点, 次の経路);
        // 進んだ方向から元に戻る
        ++各交点における通過可能な辺の数[現在の交点の位置]; //★変更ポイント★
        現在の交点の位置, 現在の得点, 現在の経路 = back(次の交点の位置, 次の得点, 次の経路, 各進行方向);
    }
    ++各交点における通過可能な辺の数[現在の交点の位置]; //★変更ポイント★
}

枝刈りその3：交点を2色に塗り分け(カラーリング)

　上記までの擬似コードでは、辺を1つ通過する度に「ゴールの交点における判定」や「次の交点に移動する処理」を行ってきました。
　ですが、一度に2つの辺を移動できれば、再帰関数を呼ぶ回数を減らすことができます。
(辺を1つづつ通過すると「行って戻る」といった意味のないムーヴも一応参照してしまうが、それが無くせるということ)

　また、このアイディアを実装する前に、交点を交互に色分け(カラーリング)してみます。
　すると、「一度に2つの辺を移動」した際は、必ず同じ色の交点にしか行かない(白→白→白→……など)のです。

　つまり、次のようなアルゴリズムになります。

• 「スタートの交点(Sマス)」と「ゴールの交点(Gマス)」の「色」を、剰余演算などで判定する
• SマスとGマスの「色」が異なる場合は、1辺だけ進んで同じ「色」に揃える
• SマスとGマスの「色」が揃っている or 揃った後に、「2辺移動」で探索を行う

※補足1：相互再帰による実装

　当初、上記のような色分けを行った後に、次のようなアルゴリズムを実装していました。
　これで「ゴールしたかの判定」の処理を呼び出す量を半分ほど削減できていたのですが、「2辺移動」のインパクトには劣りますね……。
　(再帰関数A内では再帰関数Bを呼び、再帰関数B内では再帰関数Aを呼びます)

• 「スタートの交点(Sマス)」と「ゴールの交点(Gマス)」の「色」を、剰余演算などで判定する
• SマスとGマスの「色」が異なる場合は、「ゴールしたかの判定を行わない」再帰関数Aを使用する
• SマスとGマスの「色」が同じ場合は、「ゴールしたかの判定を行なう」再帰関数Bを使用する

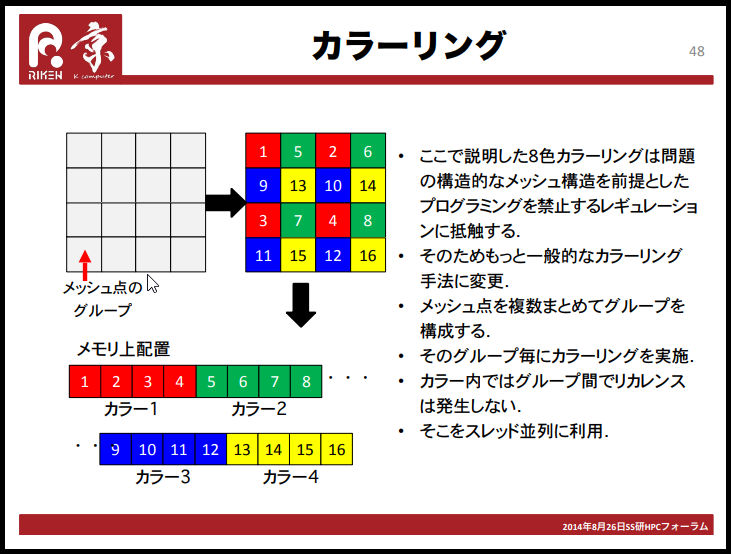
※補足2：カラーリングは3色以上行うケースもある

　上記のように「カラーリングによって得られる特徴を利用する」戦略は、2色塗り分けだけとは限りません。
　例えば数値シミュレーションの分野では、要素を色分けすることによって、「CPUを複数動かして作業を分担させる」並列演算に利用することがよくあります。
　代数的ブロック化多色順序付け法のオープンソース実装を公開しました！ - Fixstars Tech Blog /proc/cpuinfo

その際には、2色に塗り分ける他に、4色や8色に塗り分ける方式もあるそうです。
　参考資料→新ベンチマークプログラム：HPCGの概要と「京」における性能

(画像は参考資料より引用)

枝刈りその4：見込みのない経路を途中で打ち切る

「到底最高得点になりえないようなルートを進んでいたケース」を枝刈りによって排除することができれば、探索時間を大幅に節約できるでしょう。
　そこで、「探索途中の経路・盤面から最高得点の上界を予測する」ことにより、それが既に得られている最高得点より低かった際に打ち切る……といったアイディアが考えられます。
　ただ、「上界をどう予測するか」がネックで、

• 方式1：探索開始時の状況を元に算出する(精度は低いが計算量は少ない)
• 方式2：再帰関数の冒頭で毎回算出する(精度は高いが計算量は多い)

と一長一短になります。例えば以前の記事で取り上げた7x7交点の問題では、

• 「*」が付く辺は「*2」が2つ、「*3」が2つ
• 「+」が付く辺は54個で、足される数字の合計は148

ですので、問題開始時の上界は $(1+148)\times 2\times 2\times 3\times 3=5364$となります(最初の1は初期得点)。
　方式1だと「現在の得点が1未満である」ケースしか枝刈りされませんが、方式2だと例えば「現在の最高得点が3000で『*』辺が余っておらず、現在の得点が2800点しかない」といったケースも枝刈りされます。しかし方式2にしても、毎回盤面全体の「どの辺が使用可能か」を洗い出すのはコストが大きすぎると予想されますので、実装に注意が必要でしょう。
注意して実装しました。ポイントを擬似コードで示します。

// 「\*」全体の積である`mul_value`と、「+」全体の和である`add_value`を計算しておく
mul_value, add_value = pre_calc(盤面);

void dfs(現在の交点の位置, 現在の得点, 現在の経路){
    // ゴールの交点に着いた際の処理
    if(現在の交点の位置 == ゴールの交点の位置){
        if(現在の得点 > 最高得点){
            最高の得点 = 現在の得点;
            最高の経路 = 現在の経路;
        }
    }
    // 予測される最終得点の上界と、現時点で分かっている最高得点とを比較する
    if((現在の得点 + add_value) * mul_value < 最高得点)  //★変更ポイント★
        continue;                                      //★変更ポイント★
    // 交点から別の交点に進む
    for(各進行方向 : 全進行方向){
        // 既に通ったことのある辺を通過するルートは行けない
        if(各進行方向が既に通ったことのある辺である){
            continue;
        }
        // ある方向に進む
        次の交点の位置, 次の得点, 次の経路 = move(現在の交点の位置, 現在の得点, 現在の経路, 各進行方向);
        // mul_valueとadd_valueを移動に伴い変更する              //★変更ポイント★
        //現在の交点の位置→次の交点の位置における演算              //★変更ポイント★
        Operation ope = get_ope(在の交点の位置, 次の交点の位置);  //★変更ポイント★
        //演算の種類によって処理を分岐する            //★変更ポイント★
        if(ope.type == OperationType::Multi){      //★変更ポイント★
            // 掛け算なら、その掛け算を戻す処理       //★変更ポイント★
            mul_value /= ope.mul_value;            //★変更ポイント★
        }else if(ope.type == OperationType::Add){  //★変更ポイント★
            // 足し算なら、その足し算を戻す処理       //★変更ポイント★
            add_value -= ope.add_value;            //★変更ポイント★
        }                                          //★変更ポイント★
        // 再帰を1段階進める
        dfs(次の交点の位置, 次の得点, 次の経路);
        // 進んだ方向から元に戻る
        現在の交点の位置, 現在の得点, 現在の経路 = back(次の交点の位置, 次の得点, 次の経路, 各進行方向);
        if(ope.type == OperationType::Multi){      //★変更ポイント★
            // 掛け算なら、その掛け算を進める処理     //★変更ポイント★
            mul_value *= ope.mul_value;            //★変更ポイント★
        }else if(ope.type == OperationType::Add){  //★変更ポイント★
            // 足し算なら、その足し算を進める処理     //★変更ポイント★
            add_value += ope.add_value;            //★変更ポイント★
        }                                          //★変更ポイント★
    }
}

　ちなみに枝刈りを行う際は、「*」の記号が問題盤面に少ないほうがいいです。
　なぜなら、「*」の記号が多い＝上界が大きくなる＝打ち切りが行われない確率が大きいからです。
　また、問題を小問題に分割→並列演算させる際は、上記の「最高の得点」部分をグローバル変数にするなどして共有し、std::mutexなどで調停しながら同期させた方がいいです。なぜなら、こうすることにより、「他スレッドが解いた小問題によって打ち切りの精度が上がる」からです。軽く実験したところ、数割ほど計算時間を削減する効果がありました。

その他高速化のためのアイディア

　主なものを箇条書きで示します。基本なことばかりですが、なまじ再帰回数が多くなるのでその効果が大きいです。

• データをなるべくコピーしない(参照・メンバ変数など)
• 関数の引数を利用する
• 演算時の判定文を無くす・積和演算に置き換える
• プロファイリングで処理が重い箇所を見つける
• 高速化のためにコードを変更した際は、速くなったかどうかを統計的に確かめる(t検定など)
• 並列化を行う際は慎重に。バグの温床になりうるだけでなく、オーバーヘッドもそれなりにあるので注意！

　ここで並列化についてですが、かつて別のパズルを解いた際に使用した手法(スレッド数を自動で増やしたり減らしたりする)を使用したところ、スレッド生成コストが重いというドツボにはまりましたorz
　そこで、Jakob Progsch様のスレッドプールライブラリを利用しつつ、並列化に使用するスレッド数×100程度の小問題を幅優先探索で作成して分担させるといった単純な手法によって並列化に成功しました。
(ちなみに↑の用途ならOpenMPでも全然こと足りるのですが、Visual StudioだとOpenMPを有効にするとPGOビルドできないといった重大な問題ががが)