2017/12/25 追記
続編記事ができました。ぜひご覧ください。
ペンシルパズル「ペーパーチャレラン」をプログラミングで解いてみる その2
2017/12/16 追記
このパズルについて研究したのは私ぐらいだろう……と思っていましたが、少なくとも2件、別の研究が見つかりました。
・東京農工大学 工学部 情報コミュニケーション工学科の方々による研究論文「遺伝的アルゴリズムを用いた計算迷路の解法」。よく見れば2006年と書いてある……私(2014年)より8年も前だとは!
・「計算迷路チャレランを無慈悲にコンピュータで解く」と題されたプログラム。こちらは2016年に作られたらしい。
2016/04/24 追記
この記事がチャレランの公式に捕捉されました。
パズルをコンピューターで解いていたら、公式が取り上げてくださった件について - Togetter
概要
私が中学生の頃、学校の授業でこういったペーパーが配られました。
http://www.challeran.jp/crland/pe-cha/paper-challeran/0705/0705-247.pdf
当時は深く考えもせず「解き」、クラスの友人達と高得点を競ったものです。授業が終わっても家で頑張ってルートを考えた結果、最大で3000点を超えたとおぼろげながらに記憶しています。今でもその時のペーパーは保存していますが、特に貼る必要はないでしょう。
それから時が過ぎ、大人になってからふと、このペーパーのことを思い出しました。何とか探し当て、書かれていたワードからネット検索をし、そして遂に本家サイトへ辿り着いたのです。
- 正式名称:「ペーパーチャレラン第247弾0705-247 めるまがピピタ45号」
- 通称:「計算迷路チャレラン」
- 著作権表記:©日本子どもチャレンジランキング連盟 考案者:伊藤亮介
初めてサイトを見つけた際、感慨深かったと同時に、こんな決意が湧いてきました。
「やっと見つけたぞ、勝負だ!」
このページは、そうした決意を胸に、このパズルと格闘した実際の記録になります。
※以下の記録は、およそ2年前に書かれたものになります。
問題についての整理
問題の遊び方は次のページに書いてあります。
http://www.challeran.jp/crland/pe-cha/paper-challeran/0705/setumei.html
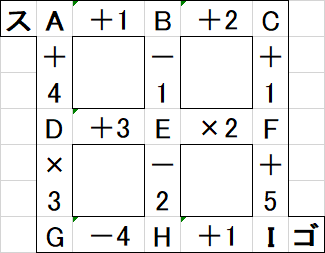
……とだけ書くのもアレなので補足説明を。仮に、次のような問題があったとします。
ここで、次のような条件が与えられたとします。
- スタートからゴールまで行った際に、最初の持ち点(1点)をなるべく増やしたい
- 道を1つ通過すると、その間に書かれている演算が行われる。例えば、場所Aにおいて1点持っている際にDへ移動した際、+4点されて結局5点となる
- 演算子は(恐らく)「+」「-」「×」の3つ。演算のうち、数字部分は(今のところ)1桁だけ
- 同じ道は2度通れないが、同じ場所は複数回通れる
この際、仮にス→A→D→G→H→I→ゴと進むと、(1+4)×3-4+1=12点となります。一方、ス→A→B→C→F→E→D→G→H→I→ゴと進むと、
((1+1+2+1)×2+3)×3-4+1=36点となります。なるべく点数を増やしたいので、この場合は後者を採用すべきです(ちなみにこの問題の最適解は36点)。
ちなみにこの「点数を競う」という性質から、「子供がゲーム感覚で楽しく計算を学べる」ということで人気を博したのがペーパーチャレランです。上記ルールは「計算迷路チャレラン」ですが、サイトにある通り、他にも様々なチャレランが存在します。
問題の難しさ
問題を見て、「これ面倒そうだな」と思った方はいらっしゃるでしょうか。実はそれ、大当たりです。
最適解を探すのがNP問題なのは言うまでもありませんが、その探索方法が問題なのです。計算量爆発を示すあの有名な動画は2012年に流行りましたが、あの問題では「同じ場所を2度通らず」「経路数を数えるだけ」といった条件でした。
『フカシギの数え方』 おねえさんといっしょ! みんなで数えてみよう!
一方、今回の問題では「同じ場所は2度通っていい」上、「経路数だけでなく最適解の値と経路を求めたい」のです。つまり、このペーパーチャレランは、フカシギの数え方よりも難しい超難問と言えます。
例えば、ペーパーチャレランで「場所の数」が6×6である場合、左上から右下に抜ける経路数は全部で1086297184通りです。一方、フカシギの数え方のルールのもとでは、同条件で1262816通りです。この時点で860倍も差があるのですから、後は推して知るべしでしょう。
冒頭に出てきた問題は「場所の数」が7x7ですが、NP問題である以上膨大な経路数であることが予測されます。しかも、Simpathのような強力な手法は今回使えそうにありません(たぶん)。つまり、全力で全探索して解を見つけるしか無いのです。
ちなみに**人類が冒頭の問題を解いた記録**によると、最高でも中学生の部で3857点だそうです。
高速化手法、演算時間の推移
まず、右も左も分からない頃はとにかく正確に実装することを第一に心がけました。その結果、次のような実装になっていました。
- 「次に移動できる座標」は計算で求める
- 「ある方向に移動できるか」は**vector<bool>**を使用
- シングルスレッドで動作。ただのDFS
当然これでは遅すぎるので、数ヶ月掛けてコツコツと高速化に取り組みました。その結果、次のような実装になりました。
- 「次に移動できる座標」はあらかじめ配列に入れておく
- 「ある方向に移動できるか」は普通の配列を使用。ただし、配列内はビットで管理されており、ビット演算によって移動できるかのフラグ・移動先座標・演算の種類・演算させる数字を取り出す
- マルチスレッドで動作。全コアをOpenMPで使いきれるように、最初はBFSで部分盤面を増やしてから、それを各コアに割り当てる仕様。各部分盤面を保存することで、それぞれを別のコンピュータで解かせることすら可能になった
どれほど速くなったかですが、手元に記録があります。かつて、ペーパーチャレランにはネット応募可能な挑戦問題があり、定期的に解答を募っていました。一応ルール説明にはコンピュータ禁止とありましたが、もう投稿できない以上関係ありません。その中でNo.25の問題について、**「A~Pまでの任意の2点(重複禁止)を選んでチャレランして最高得点を目指す」というルールに沿ってプログラムを走らせることで性能をテストしました。
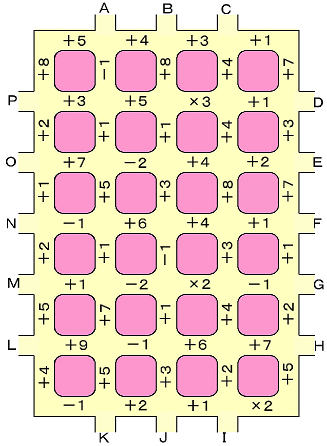
その結果、初期の頃のプログラムでは、最適解(1764点)を得るのに実時間で88078.02[s]**掛かりました。しかし、数カ月後、同じマシン(64bitWin7, Core i5-3210M)で改良したコードを走らせたところ、**29120.2030[s]**まで短縮されたのです。その性能差、実に3倍。しかも、数カ月後には複数マシンで分散処理も可能でしたので、現実的な時間で解けることになります。
ちなみに分散処理には、次のようなバッチファイルを使いました。
prompt $G
IF EXIST file_001_001.txt IF NOT EXIST file_001_001_ans.txt A_VS11.exe file_001_001.txt -1 -1 512 > file_001_001_ans.txt
IF EXIST file_001_002.txt IF NOT EXIST file_001_002_ans.txt A_VS11.exe file_001_002.txt -1 -1 512 > file_001_002_ans.txt
IF EXIST file_001_003.txt IF NOT EXIST file_001_003_ans.txt A_VS11.exe file_001_003.txt -1 -1 512 > file_001_003_ans.txt
(以下略)
要するに、**「問題ファイルが存在し、解答ファイルが存在しない際、問題ファイルを読み込み結果を標準出力→リダイレクトで解答ファイルへ出力する」**ということです。これの利点としては、リダイレクトだとプログラムが実行した瞬間に解答ファイルが作成されるので、同じ問題を複数台のPCが解いてしまうことがありません。言うなれば、Windowsのファイルシステムをセマフォとして利用したわけですね(当然LANで繋がれていること前提)。ちなみに冒頭に「pause」という文を入れておけば、「全パソコンでバッチファイルをとりあえず開いた後、走りながら各パソコンのエンターキーを押すだけで(ほぼ)同時に計算できる」といった芸当も可能です。
最終結果
こうして数ヶ月プログラムおよびパソコン群と格闘した末、ようやく最適解を得ることができました。具体的にはこんな感じです。42番から6番へ抜けるルートが最適解(4091点)であることが、延々と計算した末に確かめられました。
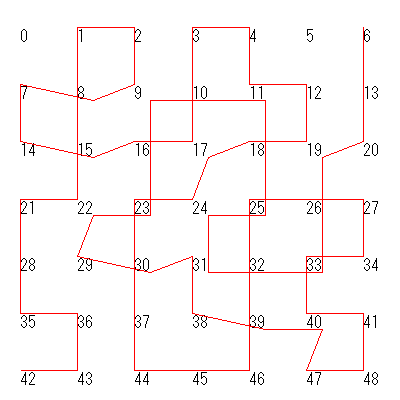
ちなみに最適解は同点数で他に3つ見つかりましたが、プログラムの仕様上**「(分割した部分問題において)元々の点数を上回らないと記録されない」(1つの入力から最適解は1つしか出されない)ようにしたので本来はもっと多くあることでしょう。ですが、バグがない限り、これより上回る解は存在しないはずです。
なお、必要な演算資源ですが、Intel Core i7-4770のマシンをWindows(64bit)で回した場合、1台で動かした場合およそ17.2日掛かると推測されました。(もちろん実際には部分問題を毎日ちょくちょく**解かせる作業を繰り返しています)
また、問題の性質上並列化しやすかったのも幸いしました。部分問題に分割できなければ悲惨だったでしょうから――。
長年の疑問が晴れた時、モニタの前で小躍りしたことをよく覚えています。関係者各位には深く感謝いたします。