概要
この2つでやれることはやり尽くした……と思ったのですが、ふと気が向いてコードをビットボードで書き直してみました。
すると大幅に高速化できたので報告します。
問題をおさらい
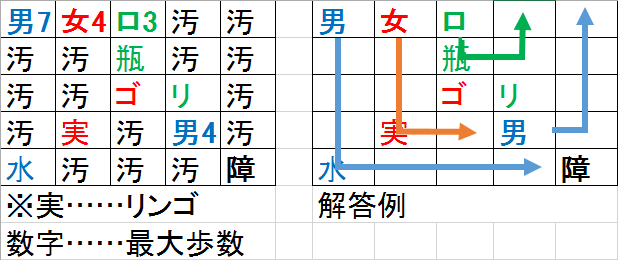
ルール
- 男の子・女の子・ロボット(以下掃除人)の移動するルートを決めましょう。
- ルートは、ルームにおけるマスを横切るか、真ん中で折れ曲がります。
- マスは最初、「拭かれていない床」「男の子」「女の子」「ロボット」「水たまり」「リンゴ」「ビン」「ゴミ箱」「リサイクル箱」「障害物」で初期化されています(「男の子」「女の子」「ロボット」は単なる初期位置)。
- 掃除人は各0人以上、全体で1人以上存在します。
- また、各掃除人は最大歩数が設定されており、それ以上マスを進むことができません。
- 掃除人が「拭かれていない床」を通過すると**「拭かれた床」に変わります**。また、男の子が「水たまり」、女の子が「リンゴ」、**ロボットが「ビン」**のマスを通過すると同様に「拭かれた床」になります。
- 女の子が「リンゴ」のマスを通過すると内部的にリンゴがストックされ、「ゴミ箱」のマスの隣(上下左右のどれか)を通過しないとそれが無くなりません。同様のことが、ロボットとビンとリサイクル箱にも言えます。なお、一度隣を通過した後に再度拾った場合は、再度隣を通過して捨てなければなりません。
- ルートを走る際、掃除人はどれも1マスづつ同時に進行します。掃除人が2人以上同時に同じマスに鉢合わせした場合、その周囲1マス(8方向)の「拭かれていない床」が「拭かれた床」になります。
- 全ての掃除人がルートを走り切った際に、全ての**「拭かれていない床」「水たまり」「リンゴ」「ビン」が「拭かれた床」になっており、かつどの女の子・ロボットもリンゴ・ビンをストックしていない**場合に清掃成功となります。
- なお、掃除人がいた初期座標は、既に「拭かれた床」であるものとします。
サンプル問題
解答の方針
- 内部データを初期化
- 再帰処理によって、各掃除人を1マスづつ動かす
- 動かす→再帰を1段階進める→戻す
- 掃除人が動く毎に、「拭かれていない床が拭かれる」「水たまり・リンゴ・ビンが消える」「それに伴い女の子・ロボットのストック状況も変わる」「ゴミ箱・リサイクル箱の隣を通るとストックが無くなる」ので、元に戻す際は注意しましょう
- また、2マス間で往復するようなことを防ぐため、「直前に居たマスがどこか」ぐらいは記憶しておくことを推奨
- 「まだ拭いてない床を優先して拭くようにオーダーリング」したら速いかと思ったらそうでもなかったでござるorz
- 掃除人が全員動いたことを確認し、また1マスづつ動かす
- この際に、ルール8.の処理が行われるので注意する
- また、枝刈りとして、「どの掃除人でも拭けない床が見つかったら見込みなしと扱う」ようにすると大幅に高速化できる
- 全員が動き終わったら、床が全て拭かれているかを確認する
- 「拭かれてない床がない」「水たまり・リンゴ・ビンがない」「ストックがない」なら完了となる
- 普通に考えるとコストが高そうだが、ビットボードを使えばマシになる(後述)
ビットボード戦略
従来のコードでは、盤面をただの2次元配列で表現していました。
もちろん直感的で分かりやすい面はあるのですが、例えば「全ての床が拭かれているかを判定するためにループを回す必要がある」など、速度重視の設計ではなかったことは否めません。
他にもビットボードの方が速くなりそうな処理があったので、ポイントごとに解説します。
用意するビットボード
| 種類 | ビットが1 | ビットが0 | 変化 |
|---|---|---|---|
| 汚れた床 | 汚れている | 汚れていない | する |
| 水たまり | 残っている | 残っていない | する |
| リンゴ | 残っている | 残っていない | する |
| ビン | 残っている | 残っていない | する |
| ゴミ箱 | 隣接している | 隣接していない | しない |
| リサイクル箱 | 隣接している | 隣接していない | しない |
ここで注意したいのが、下2つのビットボードは、そのものの位置でなく、その隣接する位置のマスのビットを1にしているということです(ルール上その方が都合がいい)。
なお、以下の説明では、「○○のビットボード」のことを【○○】と記述します。また、パズルの盤面が最大9x9なことから、ビットボードの表現としてはSIMD intrinsicで_m128i型を利用することにします。
掃除人の移動
ある掃除人が移動した際、盤面に次のような変化が発生します。
- 汚れた床が拭かれて綺麗になる
- 掃除人が男の子なら、床から水たまりが無くなる
- 掃除人が女の子なら、床からリンゴが無くなり、女の子がリンゴをストックする
- 掃除人が女の子で、かつストックがあるなら、ゴミ箱の隣を通過するとストックが無くなる
- (下2つは、女の子→ロボット、リンゴ→ビン、ゴミ箱→リサイクル箱と置き換えても成立)
これを上記のビットボードで再現すると、次のような処理になります。
- 【汚れた床】のビットが1つ0になる(元から0だった場合はそのまま)
- 掃除人が男の子なら、【水たまり】のビットが1つ0になる(同上)
- 掃除人が女の子なら、【リンゴ】のビットが1つ0になり(同上)、ストックが発生する
- 掃除人が女の子で、かつストックがあるなら、【ゴミ箱】の当該位置のビットが1だった場合、ストックが無くなる
- (下2つは、女の子→ロボット、リンゴ→ビン、ゴミ箱→リサイクル箱と置き換えても成立)
ピンポイントにビットを操作するには、「1ビットだけ立ったビットボードを位置をズラしつつ配列で用意してAND・OR・ANDNOT・XORする」のが手っ取り早いので事前に準備しましょう。unionを組んだ上で_m128iを小さな単位毎に操作……してもいいですが、どちらにせよテーブルアクセスした方が速いと思われますので。
床が全て拭かれているかを判定
終了判定に「拭かれてない床がない」「水たまり・リンゴ・ビンがない」「ストックがない」が必要なのは前述しましたが、前2つについてはビットボードで大幅に高速化できます。
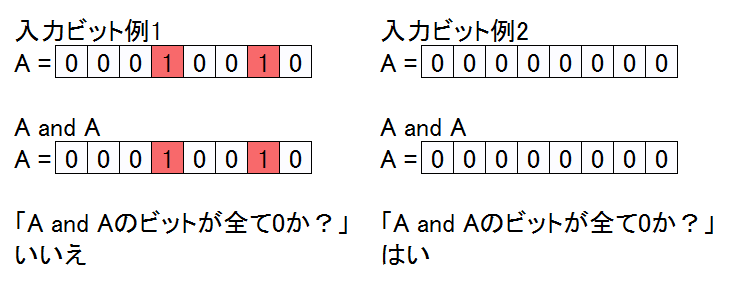
要するに「全ビットが0ならば拭けている」ので、ビット演算を駆使すればいいのですが……SIMD intrinsicの場合、実は単にビットカウントするよりも速い判定方法があります。
SSE4には「テスト組み込み関数」と呼ばれるものがあり、これを使うと「2つの入力をANDした際のビットが全て0かどうか」を判定できます。これがどう役立つかですが、入力2つを同じ値にすることで、入力のビットが全て0であるか否かを判定できることになります。具体的には下の図をご覧ください。
探索の枝刈り
解答の指針に「どの掃除人でも拭けない床が見つかったら見込みなしと扱う」と書いていたところです。
実際は非常に難しい概念であり、現在も試行錯誤し続けているところです。
枝刈り1:その床を拭けるか?
従来実装した枝刈りでは、「いずれかの掃除人が掃除可能かを各マス毎に判定する」といったコードを書いていました。$O(盤面サイズ×掃除人の数)$なので当然重く、ビットボードで高速化できないかと考えた結果、次のような発想に思い至りました。
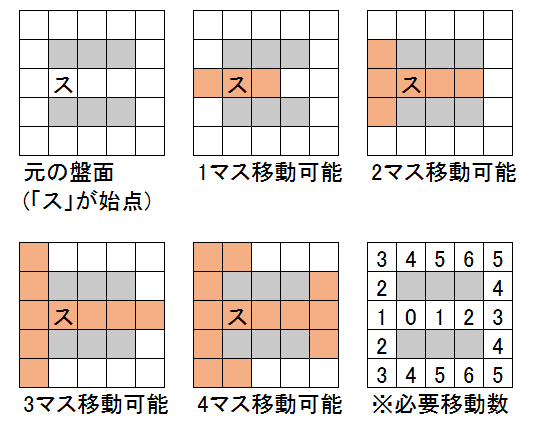
・ステップ1⇒盤面の各マスからn歩進んだ際にどこまで行けるかを記したビットボードを作成する
例えば画像例のように、移動可能なマスの部分のビットを1にしたビットボードを配列として保持します。
一見メモリを食いそうですが、パズルのサイズが9x9で20マス移動可能だとしても25KBしかないのでそれほどでもないです。
・ステップ2⇒掃除人毎に、ステップ1のビットボードを重ね合わせたものを作成する
細かい説明は不要でしょう。OR演算をすれば一発で重なります。
・ステップ3⇒ステップ2のビットボードが【汚れた床】を内包するかを判定する
ここで「AがBを内包する」とは、「Bで立っているビットの位置はAでも全て立っている」ということです。
例えば「0x1101」は「0x0101」を内包していますが、「0x1010」は内包していません。
これを判定するためには、「A and Bを計算し、それがBと等しいか」を判定するのがいいと考えました。
ところがSIMD intrinsicには同値判定が無いため(「全体」ではなく「8bit毎」とかならある)、「AがBと等しい」を「A xor Bの計算結果が0と等しいか」と判定することにしました。0と等しいかの判定には前述のテスト組み込み関数が使えますので、結果として判定できていることになります。
枝刈り2:その水たまり・リンゴ・ビンを拭けるか?
枝刈り1の応用ですぐ解けます。つまり、ステップ2のようなビットボードを掃除人毎に作成しておき、男の子なら水たまり・女の子ならリンゴ・ロボットならビンの位置を記したビットボードを内包するかを判定すればいいのです。
枝刈り3:ゴミ箱・リサイクル箱にたどり着けるか?
これは今回新しく取り入れた枝刈りです。ストックを持っている女の子・ロボットがゴミ箱・リサイクル箱にたどり着けない場合、そこからどう探索しても正解にはなりません。逆に言えば、いずれかの位置に辿り着けるのなら枝刈りできないことになります。
この概念は内包でなく、単純に「AND演算子た結果が0と等しいか」を判定すれば済みます。
擬似コード
【男の子の移動可能位置】を初期化
【女の子の移動可能位置】を初期化
【ロボットの移動可能位置】を初期化
for (const auto &掃除人 : 掃除人全体) {
switch (掃除人の種類) {
case 男の子:
【男の子の移動可能位置】に、【当該掃除人の移動可能位置】を重ね合わせ
break;
case 女の子:
// 枝刈り3
if (当該掃除人がストック持ち && (【当該掃除人の移動可能位置】 & 【ゴミ箱の周囲】)が重なっていない){
return false; //枝刈りを実行
}
【女の子の移動可能位置】に、【当該掃除人の移動可能位置】を重ね合わせ
break;
case ロボット:
// 枝刈り3
if (当該掃除人がストック持ち && (【当該掃除人の移動可能位置】 & 【リサイクル箱の周囲】)が重なっていない){
return false; //枝刈りを実行
}
【ロボットの移動可能位置】に、【当該掃除人の移動可能位置】を重ね合わせ
break;
}
}
【全員の移動可能位置】 = 【男の子の移動可能位置】 | 【女の子の移動可能位置】 | 【ロボットの移動可能位置】
// 枝刈り1
if(【全員の移動可能位置】が【汚れた床】を内包していない){
return false; //枝刈りを実行
}
// 枝刈り2
if((【男の子の移動可能位置】が【水たまり】を内包していない)
|| (【女の子の移動可能位置】が【リンゴ】を内包していない)
|| (【ロボットの移動可能位置】が【ビン】を内包していない)){
return false; //枝刈りを実行
}
実験結果
上記を元に書き直したもののリポジトリを公開しています。
ただし、まだ開発途中の代物であり、実用上はSweepOptimizerに付属する盤面ディタも併用することになると思われます(入力データフォーマットは同一)。
また、並列演算のロジックを仕込もうとしましたがあまりに難解だったので頓挫中ですorz
とはいえ探索速度はかなり速くなっており、枝刈り3を実装する前ですら問題44を2.2秒で解き、枝刈り3を実装すると1.7秒で解くことに成功しました。旧版だと8コア使っても3.4秒だったことを考えると、ビットボードが想像以上に効いている印象です。