【以下追記】
numpy のバージョンが 1.23 以上だと、astrodendro 内のパラメータの計算の中で
module 'numpy' has no attribute 'asscalar'
とエラーが出ます。
astrodendro はおそらくもうアップデートされないので、numpy のバージョンを下げる (もしくは自分でastrodendroの中身を修正する) 必要があります。例えば、一時的な解決策として、解析ディレクトリで
pip install 'numpy==1.22.4' -t ./
などとして対応してください。
【以上追記】
本記事では、以前の記事 (天文データ解析入門 その6 (astrodendroの使い方: 基本編)) よりも一歩進んだ使い方について記述します。
今回も、例として国立天文台の FUGIN プロジェクトで得られた野辺山45m電波望遠鏡の CO 輝線のアーカイブデータを用います。データは
http://jvo.nao.ac.jp/portal/nobeyama/
から
FGN_03100+0000_2x2_12CO_v1.00_cube.fits
FGN_03100+0000_2x2_13CO_v1.00_cube.fits
の2つをダウンロードします (重いです)。
12CO と 13CO のデータの grid はすでに揃っています。揃っていないデータで輝線強度比等を扱う場合は、あらかじめ天文データ解析入門 その7 (fitsのregrid) を参照して grid を揃えましょう。
まずは例によって必要なものを import し、fitsを読み込みます。
from astropy.io import fits
import numpy as np
from matplotlib import pyplot as plt
import aplpy
from astropy.wcs import WCS
import os
import shutil
import copy
hdu_12CO = fits.open("~/your/fits/dir/FGN_03100+0000_2x2_12CO_v1.00_cube.fits")[0] # 3D
hdu_13CO = fits.open("~/your/fits/dir/FGN_03100+0000_2x2_13CO_v1.00_cube.fits")[0] # 3D
w = WCS(hdu_12CO.header)
今回、簡単のため 2D fits で行います。
以下のような関数を定義します。
def v2ch(v, w): # v(km/s)をchに変える
x_tempo, y_tempo, v_tempo = w.wcs_pix2world(0, 0, 0, 0)
x_ch, y_ch, v_ch = w.wcs_world2pix(x_tempo, y_tempo, v*1000.0, 0)
v_ch = int(round(float(v_ch), 0))
return v_ch
def del_header_key(header, keys): # headerのkeyを消す
import copy
h = copy.deepcopy(header)
for k in keys:
try:
del h[k]
except:
pass
return h
def make_new_hdu_integ(hdu, v_start_wcs, v_end_wcs, w): # 積分強度のhduを作る
data = hdu.data
header = hdu.header
start_ch, end_ch = v2ch(v_start_wcs, w), v2ch(v_end_wcs, w)
new_data = np.nansum(data[start_ch:end_ch+1], axis=0)*header["CDELT3"]/1000.0
header = del_header_key(header, ["CRVAL3", "CRPIX3", "CRVAL3", "CDELT3", "CUNIT3", "CTYPE3", "CROTA3", "NAXIS3"])
header["NAXIS"] = 2
new_hdu = fits.PrimaryHDU(new_data, header)
return new_hdu
以下のように 2D fits を作成します。
integ_hdu_12CO = make_new_hdu_integ(hdu_12CO, 75.0, 125.0, w)
integ_hdu_13CO = make_new_hdu_integ(hdu_13CO, 75.0, 125.0, w)
# 都合上、edge の部分を NaN にします。
integ_hdu_12CO.data[0, :] = np.nan
integ_hdu_12CO.data[-1, :] = np.nan
integ_hdu_12CO.data[:, 0] = np.nan
integ_hdu_12CO.data[:, -1] = np.nan
前回と同様、以下を実行します。
Dendrogram と、統計量を出すためのものなどを import します。
from astrodendro import Dendrogram
from astrodendro.analysis import PPStatistic
import datetime
以下のように、3つのパラメータを設定します。詳しくはドキュメントを参照してください。
dendro_min_value = 5
dendro_min_delta = 25
dendro_min_npix = 100
ここまでは前回と同じです。
leaf 分岐時に任意の条件を加える (is_independent)
Dendrogram.compute の is_independent に任意の関数を渡すことによって、leaf 分岐時 (分割時) に新たな条件を課すことができます。
例として、新しい構造の peak 値がノイズレベルの 5 倍以下の場合 leaf として分岐させたくない場合を考えます。
(データのノイズレベルが均等ではない時などに便利です。)
まずはノイズレベルの map を作ります。
# rms の fits がある場合 (後ろに今回使用した ch 数と ch 幅をかけている)
rms_map = fits.getdata("~/your/fits/dir/rms.fits")*np.sqrt(77)*hdu_12CO.header["CDELT3"]/1000.0
# 数字として既知の場合 (3.0 K km/s など)
rms_map = np.ones_like(integ_hdu_12CO.data)*3.0
# cube から自分で作る場合
rms_map = np.nanstd(hdu_12CO.data[0:20], axis=0)*np.sqrt(77)*hdu_12CO.header["CDELT3"]/1000.0
# ↑ 20 ch目まで emission free かつ baseline が引けている場合
# 77 は今回積分した時の使用した ch 数
def custom_independent(structure, index=None, value=None): # peak が 5 rms 以上だと True
peak_index, peak_value = structure.get_peak()
rms = rms_map[peak_index[0], peak_index[1]]
return peak_value > rms*5.0
以下でDendrogramを実行します。結果は全て d_12CO に格納されます。
(一応時間を計測しています。)
t1 = datetime.datetime.now()
print("[dendro] started......", t1)
d_12CO = Dendrogram.compute(integ_hdu_12CO.data, min_value=dendro_min_value, min_delta=dendro_min_delta, min_npix=dendro_min_npix, verbose=False, is_independent=custom_independent)
t2 = datetime.datetime.now()
print("[dendro] finished.....", t2)
print("[dendro] total time... ", (t2 - t1).total_seconds(),"sec")
前回同様、pandas のDataFrame をゴリ押しで作ります。
w_integ = WCS(integ_hdu_12CO.header)
x_peak, y_peak, x_cen, y_cen, val_min, val_max = [], [], [], [], [], []
index_list, ancestor = [], []
n_vox, area_ellipse, area_exact, minor_sigma, major_sigma, position_angle = [], [], [], [], [], []
radius, total_flux = [], []
for s in d_12CO.leaves:
stat = PPStatistic(s)
index_list.append(s.idx)
ancestor.append(str(s.ancestor.idx))
y_ch, x_ch = s.get_peak()[0]
x_peak_, y_peak_ = w_integ.wcs_pix2world(x_ch, y_ch, 0)
x_peak.append(round(float(x_peak_), 6))
y_peak.append(round(float(y_peak_), 6))
x_cen_ch, y_cen_ch = stat.x_cen.value, stat.y_cen.value
x_cen_, y_cen_ = w_integ.wcs_pix2world(x_cen_ch, y_cen_ch, 0)
x_cen.append(round(float(x_cen_), 6))
y_cen.append(round(float(y_cen_), 6))
val_min.append(round(s.vmin, 6))
val_max.append(round(s.vmax, 6))
ind = s.indices()
n_vox.append(len(ind[0]))
area_ellipse.append(round(stat.area_ellipse.value, 6))
area_exact.append(round(stat.area_exact.value, 0))
minor_sigma.append(round(stat.minor_sigma.value, 6))
major_sigma.append(round(stat.major_sigma.value, 6))
position_angle.append(round(stat.position_angle.value, 6))
radius.append(round(stat.radius.value, 6))
total_flux.append(round(stat.stat.mom0(), 6))
results_leaves_12CO = pd.DataFrame({
'id':index_list, # ID
'ancestor':ancestor, # (最も)先祖のID
'x_peak':x_peak, # peak の位置のx座標
'y_peak':y_peak, # peak の位置のy座標
'x_cen':x_cen, # 重心位置のx座標
'y_cen':y_cen, # 重心位置のy座標
'val_min':val_min, # 構造の持つ最小値
'val_max':val_max, # 構造の持つ最大値
'n_vox':n_vox, # 構造が使っている pixel 数
'area_ellipse':area_ellipse, # 構造の重みつき 1 sigma の楕円面積 (pixel^2)
'area_exact':area_exact, # 構造が実際に使っている面積 (pixel^2)
'minor_sigma':minor_sigma, # 楕円の短軸 (pixel)
'major_sigma':major_sigma, # 楕円の長軸 (pixel)
'position_angle':position_angle, # 楕円の position angle (degree)
'radius':radius, # 楕円の長軸短軸の相乗平均 (pixel)
'total_flux':total_flux # 構造の持つ値の総和
})
leaf と trunk のコントアを描く
構造の輪郭のコントアを引きたい場合は、
mask = np.zeros(integ_hdu_12CO.data.shape, dtype=bool)
for s in d_12CO.leaves:
mask = mask | s.get_mask()
mask_hdu_12CO_leaves = fits.PrimaryHDU(mask.astype('short'), integ_hdu_12CO.header)
for s in d_12CO.trunk:
mask = mask | s.get_mask()
mask_hdu_12CO_trunk = fits.PrimaryHDU(mask.astype('short'), integ_hdu_12CO.header)
fig = plt.figure(figsize=(8, 8))
f = aplpy.FITSFigure(integ_hdu_12CO, slices=[0], convention='wells', figure=fig)
f.show_colorscale(vmin=1, vmax=800, stretch='log', cmap="Greys", aspect="equal")
f.show_contour(mask_hdu_12CO_leaves, colors='b', linewidths=0.5)
f.show_contour(mask_hdu_12CO_trunk, colors='r', linewidths=0.5)
plt.show()
構造ごとの輝線強度比を計算する
def calc_total_flux_2D(s, data):
ind = s.indices()
data_new = np.zeros_like(data)
for i in range(len(ind[0])):
data_new[ind[0][i]][ind[1][i]] = data[ind[0][i]][ind[1][i]]
return np.nansum(data_new)
以下を実行します。
leaf_flux_13CO_list = [calc_total_flux_2D(s, integ_hdu_13CO.data) for s in d_12CO.leaves] # leaf ごとに同じ場所の 13CO の強度を取得して積算
results_leaves_12CO["total_flux_13CO"] = leaf_flux_13CO_list # df に追加
試しに 12CO の flux と 13CO の flux の相関を見てみます。
plt.scatter(results_leaves_12CO["total_flux"], results_leaves_12CO["total_flux_13CO"])
plt.xscale("log")
plt.yscale("log")
plt.show()
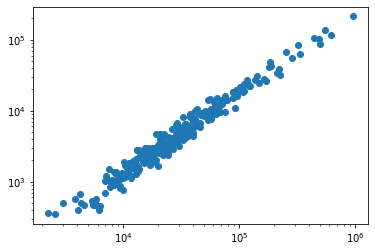
横軸と縦軸は単に pixel の合計値なので、柱密度に変換する場合などは pixel 幅などをかけてやる必要があります。
構造の fits を保存する
構造をそれぞれ fits にして保存したい時があるかと思います。
以下のような、構造の周り 1 pixel までの範囲の fits を作る関数を用意します。
def make_best_hdu_2D(structure, data, header):
header_new = copy.deepcopy(header)
ind = structure.indices()
data_new = np.zeros_like(data)
for i in range(len(ind[0])):
data_new[ind[0][i]][ind[1][i]] = data[ind[0][i]][ind[1][i]]
max_axis1, max_axis2 = np.max(ind[1]), np.max(ind[0])
min_axis1, min_axis2 = np.min(ind[1]), np.min(ind[0])
data_new = data_new[min_axis2-1:max_axis2+2, min_axis1-1:max_axis1+2]
header_new['CRPIX1'] = header_new['CRPIX1'] - (min_axis1 - 1)
header_new['CRPIX2'] = header_new['CRPIX2'] - (min_axis2 - 1)
header_new['NAXIS1'] = max_axis1 - min_axis1 + 3
header_new['NAXIS2'] = max_axis2 - min_axis2 + 3
hdu_new = fits.PrimaryHDU(data_new, header_new)
return hdu_new
まず保存先を作ります。
dir_name = "12CO_leaves"
if os.path.exists(dir_name):
shutil.rmtree(dir_name) # すでにあったら削除
os.mkdir(dir_name)
else:
os.mkdir(dir_name)
for s in d_12CO.leaves:
i = s.idx # 構造の index を取得
make_best_hdu_2D(s, integ_hdu_12CO.data, integ_hdu_12CO.header).writeto(os.path.join(dir_name, "d%s.fits"%str(i).zfill(8)))
もちろん、integ_hdu_12CO.data を integ_hdu_13CO.data にすれば 13CO の fits が作れます。
fits ができればあとは何でも好きなことができます。
今回は例として 2D で行いましたが、何箇所か書き換えるだけで 3D (cube) にも適用できます。
以上です。
リンク
目次
