Advent Calendar 5日目の記事 組合せ最適化でステンドグラスを解く
Advent Calendar 7日目の記事 組合せ最適化で因子の部屋を解く
これなに
タイルペイントを、Pythonで組合せ最適化モデルを作って解きます。
解く楽しみは、モデル化を工夫することになります。
自分でも試してみたい人は、下記を参考にしてください。
問題
- 盤面上にある、太線で区切られた部分(タイルと呼ぶ)のいくつかを黒く塗ります。
- 盤面の数字は、その右あるいは下の、1行あるいは1列のうちで、黒く塗られるマスの数を表します。
- どのタイルも、全てのマスを塗るか全てのマスを塗らずにおくかのどちらかとし、タイルの一部のマスだけを塗ってはいけません。
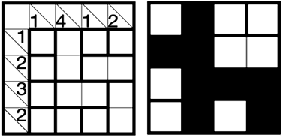
左が問題で、右が答えです。
Pythonでは、data(タイルのグループの文字)、hint_v(各行の合計)hint_h(各列の合計)、を使うことにします。
python
import pandas as pd, matplotlib.pyplot as plt
from pulp import LpProblem, lpSum, value
from ortoolpy import addbinvars
data = """\
ABCD
EBFF
GHHI
JKLI
""".splitlines()
hint_v,hint_h = [1,2,3,2],[1,4,1,2]
変数表
下記のような変数表を作成します。各行の変数(Var)は0または1をとります。
変数の値が1ならば、該当行 該当列のマスを黒く塗ります。
字は、該当マスの属するタイルのグループです。
| 行 | 列 | 字 | Var | |
|---|---|---|---|---|
| 0 | 0 | 0 | A | v000001 |
| 1 | 0 | 1 | B | v000002 |
| ... | ... | ... | ... | ... |
python
ni, nj = len(data), len(data[0])
a = pd.DataFrame([(i,j,data[i][j]) for i in range(ni)
for j in range(ni)], columns=list('行列字'))
a['Var'] = addbinvars(len(a))
a[:2]
数理モデルを作り解く
変数表ができたので、タイルペイントの解になるように、制約条件を追加し数理モデルを作成し、解きましょう。
- 各行の合計が指定された数に等しい。
- 各列の合計が指定された数に等しい。
- 各タイル内は全て塗るか塗らないか。
python
m = LpProblem()
for i in range(ni):
m += lpSum(a[a.行==i].Var) == hint_v[i]
for j in range(nj):
m += lpSum(a[a.列==j].Var) == hint_h[j]
for _,v in a.groupby('字'):
for vi, vj in zip(v.Var, v.Var[1:]):
m += vi == vj
m.solve()
結果の表示
python
a['Val'] = a.Var.apply(value)
plt.imshow((a.Val<0.5).values.reshape(ni,nj), cmap='gray', interpolation='none')
plt.show()
解けていることが確認できます。
以上