Advent Calendar 4日目の記事 組合せ最適化でエデンの園配置を証明する
Advent Calendar 6日目の記事 組合せ最適化でタイルペイントを解く
これなに
ステンドグラスを、Pythonで組合せ最適化モデルを作って解きます。
解く楽しみは、モデル化を工夫することになります。
自分でも試してみたい人は、下記を参考にしてください。
問題
- 線で区切られた部分(ピース)のいくつかを黒くぬります
- 小さな丸は、その丸が接している周囲のピースのうち、黒ピースと白ピースのどちらの数が多いかを表します
- 黒丸なら黒ピースの方が多く、白丸なら白ピースの方が多く、灰色の丸は、同数となります
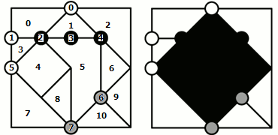
下記は、左が問題で、右が答えです。
Pythonでは、npi(ピースの数)、hint(色と周りのピース)を使うことにします。
python
from pulp import LpProblem, lpSum, value
from ortoolpy import addbinvars
npi = 11 # ピース数
hint = [s.split(',') for s in """\
W,0,1,2
W,0,3
B,0,1,3,4,5
B,1,5
B,1,2,5,6
W,3,4,7
G,5,6,9,10
G,5,7,8,10""".splitlines()]
数理モデルを作り解く
変数は、各ピースが黒(1)か白(0)にしましょう。
- ヒントが
'W':黒のピース数が半分未満 - ヒントが
'B':黒のピース数が半分超 - ヒントが
'G':黒のピース数がちょうど半分
python
m = LpProblem() # 数理モデル
v = addbinvars(npi) # 変数(黒かどうか)
for c,*lst in hint:
vlst = [v[int(i)] for i in lst] # 周囲のピースの変数
if c == 'W':
m += lpSum(vlst) <= (len(vlst) - 1) // 2
elif c == 'B':
m += lpSum(vlst) >= (len(vlst) + 2) // 2
else:
m += lpSum(vlst) == len(vlst) // 2
m.solve()
結果の表示
python
print('black:', [i for i in range(npi) if value(v[i])>0.5])
>>>
black: [1, 4, 5, 6, 8]
解けていることが確認できます。簡単ですね。
以上