Advent Calendar 6日目の記事 組合せ最適化でタイルペイントを解く
Advent Calendar 8日目の記事 組合せ最適化でのりのりを解く
これなに
因子の部屋を、Pythonで組合せ最適化モデルを作って解きます。
解く楽しみは、モデル化を工夫することになります。
自分でも試してみたい人は、下記を参考にしてください。
問題
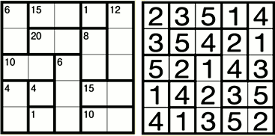
- すべてのマスに1からNまでの数字のどれかを1つずつ入ります(0は使いません)。
- タテ列、ヨコ列のどれにも、1からNまでの数字が1つずつ入ります。
- 太線で囲まれた四角形(部屋)の左上のマスに小さく書かれている数は、その部屋の各マスに入る数をすべてかけあわせた値となります。
左が問題で、右が答えです。
Pythonでは、data(部屋のグループ)、nums(グループ別の値)を使うことにします。
python
import pandas as pd
from math import log
from pulp import LpProblem, lpSum, lpDot, value
from ortoolpy import addbinvars
data = """\
ABBCD
AEEFD
GGHFD
IJHKK
ILHMM""".splitlines()
nums = {'A':6, 'B':15, 'C':1, 'D':12, 'E':20, 'F':8,
'G':10, 'H':6, 'I':4, 'J':4, 'K':15, 'L':1, 'M':10}
変数表
下記のような変数表を作成します。各行の変数(Var)は0または1をとります。
変数の値が1ならば、該当行 該当列のマスが該当の数になります。
| 行 | 列 | 数 | 字 | Var | |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | A | v000001 |
| 1 | 0 | 0 | 2 | A | v000002 |
| ... | ... | ... | ... | ... | ... |
python
nn = len(data)
a = pd.DataFrame([(i,j,k,data[i][j]) for i in range(nn)
for j in range(nn) for k in range(1,nn+1)], columns=list('行列数字'))
a['Var'] = addbinvars(len(a))
a[:2]
数理モデルを作り解く
変数表ができたので、因子の部屋の解になるように、制約条件を追加し数理モデルを作成し、解きましょう。
- 各マスに数字を1つ入れる。
-
for _,v in a.groupby(('行','列'))で1つのマスの変数がDataFrameのvに入るので、m += lpSum(v.Var) == 1とすれば、数字を1つ選ぶことになります。
-
- 各行で同じ数字は1つ。('行','数')にすれば、上記と同じです。
- 各列で同じ数字は1つ。('列','数')にすれば、上記と同じです。
- かけた数がヒントと同じ。掛け算は、
logをとれば、足し算になります。計算誤差に注意し、等号ではなく、ある幅に入るように制約をかけます。
python
m = LpProblem()
for cl in [('行','列'),('行','数'),('列','数')]:
for _,v in a.groupby(cl):
m += lpSum(v.Var) == 1
for g,v in a.groupby('字'):
e = lpDot([log(i) for i in v.数], v.Var) - log(nums[g])
m += e >= -0.0001
m += e <= 0.0001
m.solve()
結果の表示
python
a['Val'] = a.Var.apply(value)
print(a[a.Val>0.5].数.values.reshape(nn,nn))
>>>
[[2 3 5 1 4]
[3 5 4 2 1]
[5 2 1 4 3]
[1 4 2 3 5]
[4 1 3 5 2]]
解けていることが確認できます。
以上