メッシュのミラーリング
Blenderには、メッシュを対称にする機能があります(編集モードのメッシュの「対称にスナップ」)。これは、最も近い2点をマッチングさせています。
これはこれで便利なのですが、個別に最近傍ではなく、全体的にバランスよく移動したいことがあります。
ここでは、それを数理最適化で実現するアドオンを紹介します。
具体例
対称のメッシュを作成します。
-
追加のメッシュのグリッド(Y軸方向の分割数=2、サイズ=0.2) - 編集モードに入る
- 真ん中の辺を選び、
削除の辺を溶解 - 上側の中よりの8点を選び、X軸方向に
0.01移動

右上の5点を選びメッシュの対称にスナップを実行すると下記のようになります。ただし、実行ごとに変わる可能性があります。

- 2つの点が1つの点と対称になっています。
- 1つずらした方がバランスが良いのですが、個別に処理しているのでバランスが取れていません。
一方で、今回紹介するアドオンを実行すると下記のようになります。
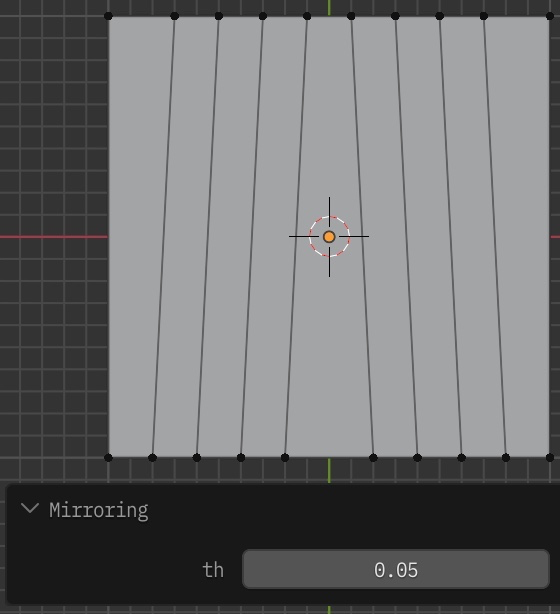
バランスよく対称になります。
インストール方法
PuLPのインストール
本アドオンは、PythonのPuLPモジュールを利用しています。
そのため、下記のように、コマンドラインでBlenderにPuLPをインストールする必要があります。コマンドラインからBlenderを操作する方法については、「Blenderのコマンドサンプル」も参考にしてください。
※ バージョンは適宜変えてください。
- macOSの場合
/Applications/Blender.app/Contents/Resources/3.2/python/bin/python3.10 -m pip install pulp
- Windowsの場合
"C:\Program Files\Blender Foundation\Blender 3.2\3.2\python\bin\python" -m pip install pulp
※ Windowsで、インストールできるのにimportでエラーになる場合は、一旦アンインストールしてから、管理者権限のコマンドプロンプトでインストールし直すとうまくいくかもしれません。
※ 実は、Python-MIPライブラリーを使いたかったのですが、Blender3.2では動かないためPuLPを用いています。
アドオンのインストール
-
GitHubのMirroringから、下記のアドオンのZIPファイルをダウンロードしてください。ZIPファイルは解凍しないでください。
-
Blenderのプリファレンスのアドオンで「インストール…」ボタンを押し、ダウンロードしたZIPファイルを選択します。
-
テスト中を選んでください。下図のようになるので、
Mesh: Mirroringにチェックを入れてください。
使い方
- 対象のオブジェクトを選んで、編集モードに入ります。
- サイドバーの編集タブを開きます。
- 固定したい方の点を選びます。標準機能とは異なり、選択した点は固定されます。選択点に対称になるように他の点が移動します。
-
Thに移動可能な距離を指定します。 -
Mirroringボタンを押します。 - 実行後、対称点が存在しない点が選択されたままになります。
※ 標準機能と異なり、X軸のみを対称にします。また、境界はx==0です。移動するのは、正の象限か負の象限のどちらかだけです。選択点の中心が存在する象限が移動しない方です。
最適化について
選択点に対してどの点を対称にするかをマッチングで決定します。マッチングなので、1対1になります。
まず、なるべくたくさんのマッチングを作るために、最大マッチング問題を解きます(1回目)。
次に、移動が少なるように、最小重み最大マッチング問題を解きます(2回目)。ただし、単純に距離を重みにすると移動が大きい点が生じる可能性があるので、正規化した距離を自乗して重みにします。
これら重みマッチング問題は、NetworkXのmax_weight_matchingで解くことができます。しかし、ここでは混合整数最適化問題として解いています。これは、制約条件の変更が容易なためです。
混合整数最適化問題とは何かについては、「組合せ最適化を使おう」を参考にしてください。
ここでは、混合整数最適化問題を定式化し、PuLPでモデル化しCBCソルバーで解きます。
定式化
変数は以下を対象に0-1変数を作成します。1がマッチングする、0がマッチングしないに対応します。
- 2点のペア。片方は固定象限の選択点。もう片方は移動可能象限で距離がTh以下の点
1回目の定式化
| 目的関数 | マッチング数 → 最大化 |
|---|---|
| 制約条件 | マッチングであること |
2回目の定式化
| 目的関数 | 正規化した移動距離の自乗和の-1倍 → 最大化 |
|---|---|
| 制約条件 | マッチングであること |
| 制約条件 | 最大マッチングであること |
アドオンのコード(Python)
実際にミラーリングするのは、execute()メソッドになります。
以上