重みマッチング問題
重みマッチング問題は、「最大重みマッチング問題、最大重み最大マッチング問題、最大重み完全マッチング問題、最小重み最大マッチング問題、最小重み完全マッチング問題」などの総称である。
| 重みマッチング問題 | 問題種類 | マッチングした辺数 |
|---|---|---|
| 最大重みマッチング問題 | 最大化 | 任意 |
| 最大重み最大マッチング問題 | 最大化 | 最大マッチング問題と等しくなければいけない |
| 最大重み完全マッチング問題 | 最大化 | 点数の半分でなければいけない |
| 最小重み最大マッチング問題 | 最小化 | 最大マッチング問題と等しくなければいけない |
| 最小重み完全マッチング問題 | 最小化 | 点数の半分でなければいけない |
- 重みは全て0以上とする。
- 最小重みマッチング問題は、空が自明な最適解なので、通常、検討対象としない。
- 「最大重みマッチング問題と最大重み最大マッチング問題と最小重み最大マッチング問題」において重みが全て1のとき、単に「最大マッチング問題」とよぶ。
- 「最大重み完全マッチング問題と最小重み完全マッチング問題」において重みが全て1のとき、単に「完全マッチング問題」とよぶ。
- 最小重み最大マッチング問題と最小重み完全マッチング問題は、当該重みを「重みの最大ー当該重み」に変えれば、最大重み最大マッチング問題と最大重み完全マッチング問題に帰着できる。
- 最大重み完全マッチング問題は、最大重み最大マッチング問題の解が完全マッチングになっている場合のみ解となる。
- これらのことから、最大重みマッチング問題と最大重み最大マッチング問題の解法があればよいことになる。
- 最大重みマッチング問題は、下記の max_weight_matching (エドモンズ法)で解ける。
- 最大重み最大マッチング問題を解く場合、下記の max_weight_matching で maxcardinality=True を指定すればよい。
- グラフが2部グラフの場合、一般のグラフより高性能の(ハンガリー法などの)アルゴリズムが存在する(参考「二部グラフの最小重み完全マッチング」)。
##最大重みマッチング問題
無向グラフ$G=(V,E)$に対し、各辺$e \in E$の重み$w(e)$が与えられているとき、$\sum_{e \in M}{w(e)}$が最大のマッチング$M$を求めよ。
##実行方法(最大重みマッチング問題)
usage
Signature: nx.max_weight_matching(G, maxcardinality=False)
Docstring:
Compute a maximum-weighted matching of G.
A matching is a subset of edges in which no node occurs more than once.
The cardinality of a matching is the number of matched edges.
The weight of a matching is the sum of the weights of its edges.
python
# CSVデータ
import pandas as pd, networkx as nx, matplotlib.pyplot as plt
from ortoolpy import graph_from_table, networkx_draw
tbn = pd.read_csv('data/node0.csv')
tbe = pd.read_csv('data/edge0.csv')
g = graph_from_table(tbn, tbe)[0]
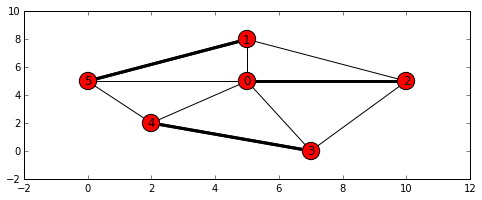
d = nx.max_weight_matching(g)
pos = networkx_draw(g)
nx.draw_networkx_edges(g, pos, width=3, edgelist=[(i, j) for i, j in d])
plt.show()
print(d)
結果
{5: 1, 1: 5, 0: 2, 2: 0, 4: 3, 3: 4}
python
# pandas.DataFrame
from ortoolpy.optimization import MaxWeightMatching
MaxWeightMatching('data/edge0.csv')
| node1 | node2 | capacity | weight | |
|---|---|---|---|---|
| 0 | 0 | 2 | 2 | 4 |
| 1 | 1 | 5 | 2 | 5 |
| 2 | 3 | 4 | 2 | 4 |
python
# 乱数データ
import networkx as nx, matplotlib.pyplot as plt
from ortoolpy import networkx_draw
g = nx.random_graphs.fast_gnp_random_graph(10, 0.3, 1)
for i, j in g.edges():
g.adj[i][j]['weight'] = 1
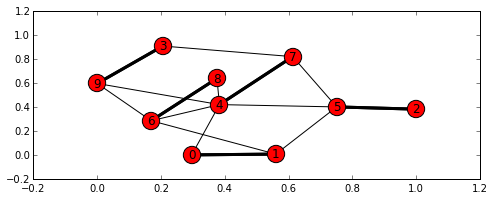
d = nx.max_weight_matching(g)
pos = networkx_draw(g, nx.spring_layout(g))
nx.draw_networkx_edges(g, pos, width=3, edgelist=[(i, j) for i, j in d])
plt.show()
##データ