本記事の動機
製造業において見込み生産を行う場合適切な生産数を算出することが重要になります。適切な生産数でない場合、例えば、見込みの生産量が実際の数量を上回った場合だと在庫が多くなり廃棄コストなどの保有リスクが増加していきます。見込みの生産量が実際の需要量を下回った場合は、製品の生産が遅れ納期遵守率の低下等のリスクが発生する可能性があります。このようなリスクを減少させるために、内示等の情報を利用して可能な限り実際の需要量を予測して生産活動を行うことになります。
他方、顧客ニーズの多様化や製品ライフサイクルの短縮化により多品種少量生産が求められています。多品種少量生産下では各製品に対する管理項目も増え、需要予測に対する工数が増加します。また、管理項目の増加に伴う見落としも考えられ、結果として需要予測の精度が落ちることも考えられます。そこで、pythonで予め需要予測モデルを作成しておき、後はデータセットの更新だけ行うようにする手法を構築できれば、開発工数のかからない多品種少量生産下における需要予測モデルを確立できるのではないかと考えたのが本記事の動機になります。
今回はそのための最初のステップとして、需要予測時に扱う時系列解析のポイントを説明し、どのような手順で実装できるかをまとめられるようにしていきたいです。また、今回実装したSARIMA、LSTM、NeuralProphetの実装方法の説明と簡単な評価をして理解を深められればと考えています。
本記事で実装する需要予測手法
時系列解析は、時間の経過に沿って並んでいるデータに対して統計的手法を用いて分析し将来データを予測する手法になります。需要のデータは日毎、週毎・・などの受注日に沿って受注量のデータが推移するため、時系列解析の手法を用いて予測することが可能です。pythonでは多様な時系列解析手法を簡単に構築できるようにライブラリが準備されており、コーディングの方法を理解すれば将来の需要を簡単に出力できます。本記事では実際に実装を行い、多品種少量生産下における需要予測が可能かどうか考えていきたいです。
なお本記事では以下の3つの手法で需要予測を実施していきます。
〇SARIMA
〇LSTM
〇NeuralProphet
本記事のデータセット、および、環境
- データセット : Store Item Demand Forecasting Challenge
- 実装環境 : google colaboratory
データセット内容、および、訓練データ設定内容
今回のデータセットは、10店舗の小売店における2013/1/1〜2017/12/31までの50品目分の販売実績となっています。内容は以下の通りです。
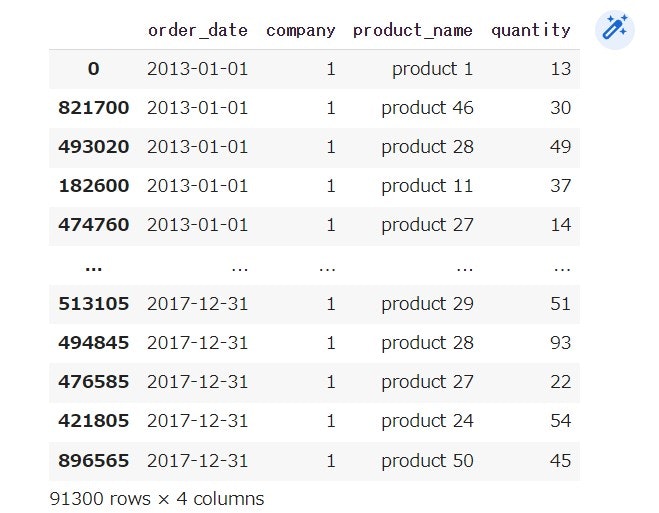
本記事の大目的は多品種の需要予測となるため、データの項目名は・storeをcompany、itemをproduct(product No)に変更し、10社の顧客に対するproduct1 ~product50の受注実績と考えていきます。今回は顧客No 1に対してを行っていきます。コーディングは以下のようになります。なお、csvで読み取ったデータフレームを「df_info」とし、顧客No 1の顧客に対して予測を行っていきます。
#列名の変更
df_info = df_info.rename(columns={'date': 'order_date', 'sales' : 'quantity', 'item' : 'product_name','store' : 'company'})
#顧客No 1 の抽出
df_company1 = df_info.query('company == 1')
df_company1 = df_company1.sort_values(by='order_date', ascending = True)
#product名の変更
df_company1["product_name"] = ["product " + str(p) for p in df_company1["product_name"]]
結果は以下のようになります。
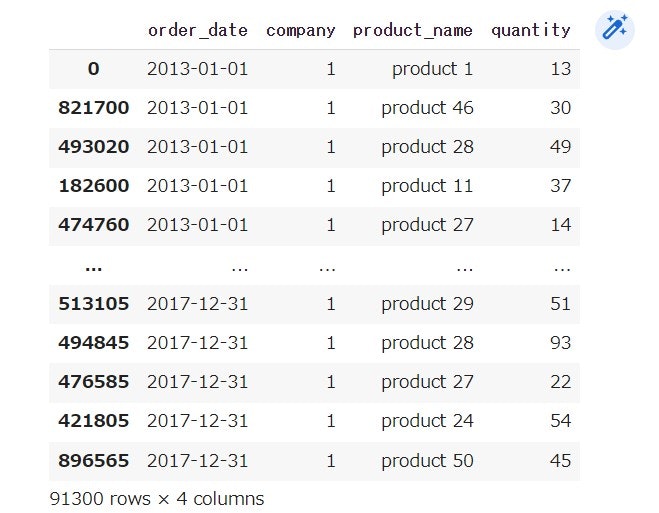
各品種のグラフを可視化してみると、数量の違いはあれど、グラフの傾向に類似点が見受けられます。何点か例として挙げます。なお、描画方法については別途後続の節のコーディングを参考にしてください。
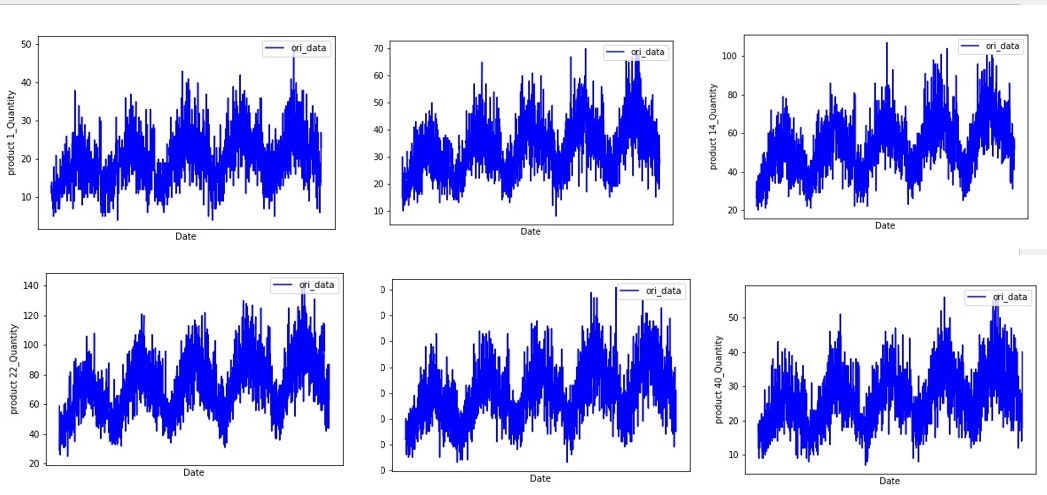
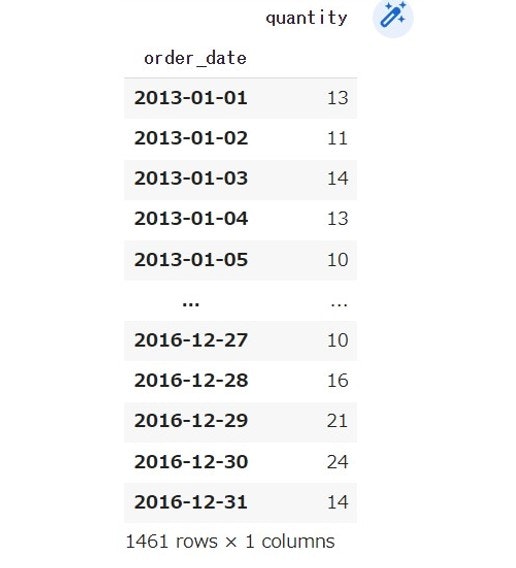
そこで多品種の予測をするにあたり、ある1品種において最もよい需要予測モデルを評価した上で適用し、そのモデルの予測値に対して重みづけを行うことにより、全品種への予測時間を短縮した上でより良いモデルを構築できると考えました。そこで今回はproduct1でのモデル構築を試みます。また訓練データは2016年までのデータとし、各需要予測モデルでは2017年の予測を実施し実際の2017年の需要と比較していきます。訓練データを以下に示します。なお、後述しますがモデルごとに項目名等の違いが存在するため注意が必要です。
時系列解析における需要なポイント
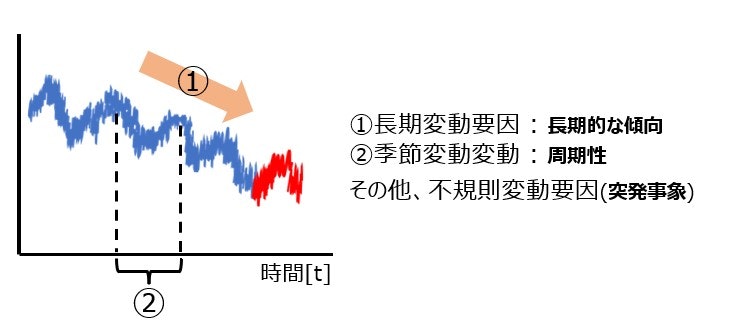
時間に沿って変動している時系列データは、上図のように、減少傾向のような長期的傾向(トレンド)を示している要因である長期変動要因(①)、周期性を示している季節変動要因(②)に加え、突発的な需要のような誤差を示す不規則変動要因が組み合わさって成立しています。これら変動要因を元の時系列データ(原系列といいます)に残したまま、時系列解析を行ってしまうと上手くいかない可能性があります。なぜなら、時間という要素を通して、実際には相関のない変動要因同士を相関があるかのように推定する可能性があるからです。そこで、原系列に対して各変動要因を除去し時間によらず変動幅が一定の時系列データ作成し、そこから各変動要因の考慮をしていき予測モデルを構築していきます。変動幅が一定であることを定常性があるといい、この定常性を作ることが需要予測では需要なポイントとなります。
定常性の作成と確認
本記事では変動要因を除去する手法として良く使われる手法である、対数変換手法と階差手法を説明します。
対数変換手法は、値に対してlogを取ることにより値の変化を緩やかにし変動要因を除去する手法です。変換するデータセットを「data」とすると、以下のように実装できます。
import numpy as np
# 対数変換
data += 1 #対数は log0 = infなので 正の値になるように処理
data = np.log10(data) #例では10を底 底がeの場合は np.log(data)
階差手法は、1つ前の時刻間の値の差分をとることで変動要因を除去する手法で、以下のように実装できます。
# 階差
data = data.diff()
定常性を確認する手法として、ADF検定と呼ばれるものがあります。ADF検定を実装して出力される2つの値「Test Statistic」、「Critical Value (5%)」において、「Test Statistic」の方が値が小さければ定常性があるということのようです。以下のように実装できます。 (参考url)
from statsmodels.tsa.stattools import adfuller
#対数変換、階差どちらかでADF検定
#対数変換
data += 1
data = np.log10(data)
# 階差
#data = data.diff()
#ADF検定
test = adfuller(data[1:])
output = pd.Series(data[0:4], index=['Test Statistic','p-value','#Lags Used','Number of Observations Used'])
#各統計量の格納
for key,value in data[4].items():
output['Critical Value (%s)'%key] = value
#Test Statistic」、「Critical Value (5%)」の比較
if output['Test Statistic'] < output['Critical Value (5%)'] :
print(pn + " ADF test")
print(dfoutput)
print("")
else :
print(pn + " は定常性ありません")
今回のデータセットに対して対数変換、階差による変動要因の除去をした後にADF検定をした結果、階差による除去が定常性を担保できそうなことが分かりました。ここでは原系列と階差のグラフの描画関数の例を記載します。
# 日の受注推移と階差を1つのグラフに描画する関数
def DrawDiff_CompareOriData(df_ori,x_title,y_title,fig_folder):
pn_list = list(df_ori["product_name"].drop_duplicates())
for pn in pn_list:
# 製品別の合計データセット作成
querystr = 'product_name == "' + pn + '"'
df_target = df_ori.query(querystr)
df_target = df_target.sort_values(by='order_date', ascending = True)
df_target = df_target.groupby('order_date').sum().reset_index()
days = list(df_target["order_date"].drop_duplicates())
# 階差
df_target["Diff_quantity"] = df_target["quantity"].diff()
# 製品の日の受注推移と階差の描画
fig, ax = plt.subplots()
ax.plot(days, df_target["quantity"],
color ="blue",label = 'ori_data')
ax.plot(days, df_target["Diff_quantity"],
color ="red",label = 'Diff')
# ラベル
ax.set_ylabel(pn + "_" + y_title)
ax.set_xlabel(x_title)
#系列
plt.legend(loc = 'upper right')
plt.show()
fig.savefig(fig_folder + pn +".jpg")
描画結果例は以下のようになります。
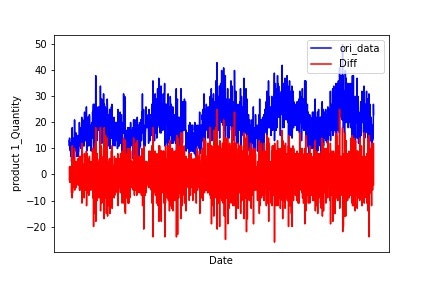
実際ADF.py部分を利用し、ADF検定を行った結果全ての製品において定常性を確認できました。
SARIMAの適用
※別途数式が気になる方は、解説サイトをご覧ください。
SARIMAモデルは、Seasonal ARIMA modelの略でARIMAというモデルに対して周期sを組み込んだ予測モデルになります。
ARIMAモデルは、AR Intergated MA modelの略で、ARモデル(AutoRegressive model : 自己回帰モデル)とMAモデル(Moving Average model : 移動平均モデル)を組み合わせたものになり、原系列にd回階差を取り定常性を担保した系列に対して、ARモデルとMAモデルを適用したモデルです。今回は1回分の階差で定常性の担保ができたため、d = 1となります。
ARモデル
ARモデル(自己回帰モデル)は、ある時刻における値が何個前までのデータに対して影響があるかを示すモデルであり、p個前の値までの影響がある場合、AR(p)と表します。ARモデルにおけるpは以下のコードで求めることができます(参考url)。
from statsmodels.tsa import ar_model
#SARIMAモデルのpの推定(ARモデルのpの推定)
def ARCparams(df_ori) :
params = []
for i in range(4): #range(N) : N個前までのデータを考慮する
#ARモデル推定
model = ar_model.AR(df_ori['quantity'][1:])
maxlag = i+1
results = model.fit(maxlag=maxlag)
# 今回最適なpを求めるにあたり、AICという指標を用います。
# AICが最小値のpが最適なものになります※別途AICは記事にしようと思います。
params.append([maxlag, results.aic])
#print(f'lag = {i+1}, aic : {results.aic}')
order_df = pd.DataFrame(params,columns=["p","AIC"])
order_df = order_df.sort_values(by = "AIC", ascending = True)
#order_dfは昇順のため、order_df.head(1)で最小のpが分かります
return order_df
product1の場合、p = 3が最小値でした。
MAモデル
MAモデル(移動平均モデル)は、ARモデルと違いある時点の値ではなく過去の誤差に対して回帰していると考え時系列データを予測するモデルです。具体的にはデータのなかで過去の不規則変動要因に着目し、これらに対して加重平均を使って現在の誤差を求めて、その時点でのデータの平均を加算して予測したい時刻の値を算出しようとするモデルです。q個前の誤差を考慮する際、MA(q)と表します。以下では、原系列と移動平均結果を比較する描画関数例を示します。
# 日の受注推移とMAを1つのグラフに描画する関数
def DrawMA_CompareOriData(df_ori,x_title,y_title,slot,fig_folder):
pn_list = list(df_ori["product_name"].drop_duplicates())
for pn in pn_list:
# 製品別の合計データセット作成
querystr = 'product_name == "' + pn + '"'
df_target = df_ori.query(querystr)
df_target = df_target.sort_values(by='order_date', ascending = True)
df_target = df_target.groupby('order_date').sum().reset_index()
days = list(df_target["order_date"].drop_duplicates())
# 移動平均
#slot : 何個前までの誤差をみるか
df_target["MA_quantity"] = df_target["quantity"].rolling(window = slot).mean()
# 製品の日の受注推移と移動平均の描画
fig, ax = plt.subplots()
ax.plot(days, df_target["quantity"],
color ="blue",label = 'ori_data')
ax.plot(days, df_target["MA_quantity"],
color ="red",label = 'MA')
# ラベル
ax.set_ylabel(pn + "_" + y_title)
ax.set_xlabel(x_title)
#系列
plt.legend(loc = 'upper right')
plt.show()
fig.savefig(fig_folder + pn +".jpg")
例として、product1の原系列に対する移動平均(q=3,5のとき)の結果例を示します。
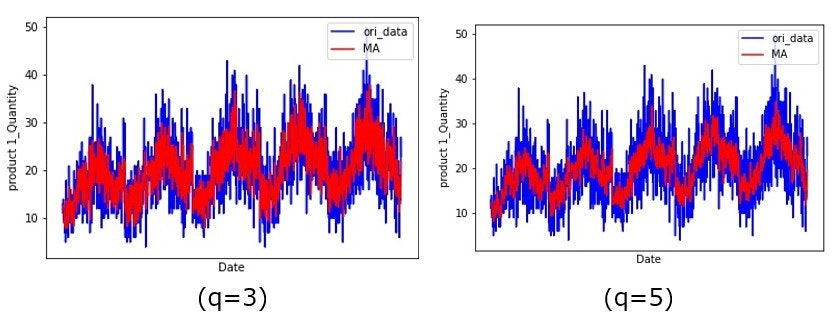
周期性(s)の考慮
ここまで、p、d、qを求め過去の時系列データとの関係性の考慮を行い、SARIMAにおけるARIMA部分における変数を探索する方法を説明しました。ここからは、周期性を求める方法として、自己相関と偏自己相関の実装方法を説明します。
自己相関はある時系列データにおける過去データとの相関を求めるものであり、偏自己相関は2つの時刻間の相関を求めるもので、間にある値の影響は取り除くものになります。例えばt1とt4の相関を見る場合、自己相関はt1、t2、t3、t4までのデータを通した相関をみるもので、偏自己相関はt1とt4の相関のみで、t2、t3の影響は考慮しないものとなります。このような性質上、強い相関がある地点において周期性があると捉えることができます。実装方法を以下に示します。
# 自己相関・偏自己相関グラフの出力
def DrawCorrelation(df_ori,lag,pn) :
fig=plt.figure(figsize=(12, 8))
df_target = df_ori.set_index("order_date")
# 自己相関係数のグラフの出力
# lag : pの推定に使用 ズラすデータ数(何個前までのデータの影響をみるか)
ax1 = fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(df_target, lags=lag, ax=ax1)
# 偏自己相関係数のグラフの出力
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(df_target, lags=lag, ax=ax2)
plt.show()
fig.savefig(fig_folder + pn +".jpg")
product1の描画例を見てみると周期が7であることが読み取れます。(周期 s = 7)
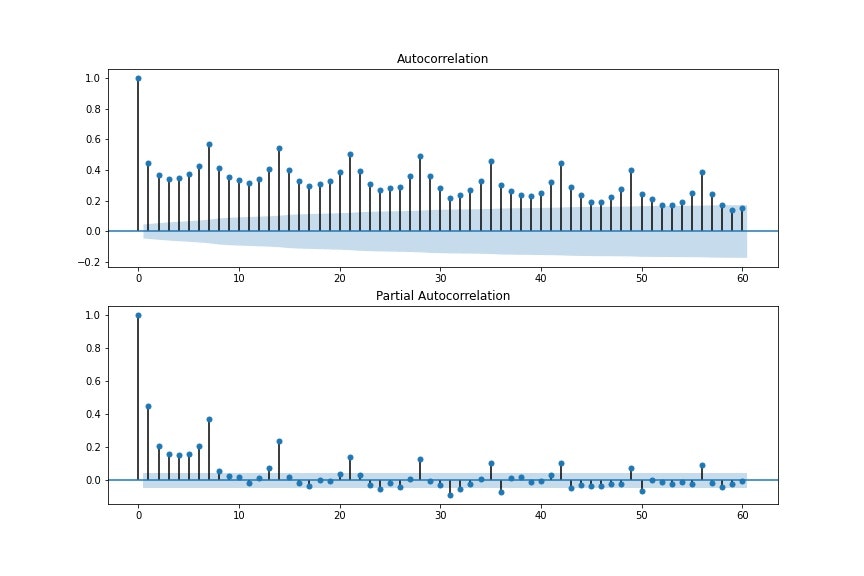
また周期性だけでなく、周期性を考慮したp、d、qであるsp(季節性自己相関)、sd(季節性導出)、sq(季節性移動平均)も求める必要があります。例えばs=7(日)の場合、sq=2は1週間前のデータと2週間前のデータの影響を受けることを示しています。
では今までの実装で出した値を参考に、最適なパラメータの探索方法を実装していきます。
SARIMAの最適パラメータの設定方法とモデル構築
SARIMAでは訓練データの日付項目をインデックスに指定する必要があり、以下のように実装します。
df_target = df_target[["order_date","quantity"]]
df_target = df_target.query("order_date <= '2016-12-31'")
# 日付項目インデックス化
df_target = df_target.set_index("order_date")
そして、最適パラメータの探索例は以下のようになります。
import itertools
import numpy as np
import statsmodels.api as sm
import warnings
#リストを一意にする関数
def get_unique_list(seq):
seen = []
return [x for x in seq if x not in seen and not seen.append(x)]
#SARIMAモデルパラメータ探索
def selectparameter(DATA,s,
p_list,d_list,q_list,
sp_list,sd_list,sq_list):
p = p_list
d = d_list
q = q_list
sp = sp_list
sd = sd_list
sq = sq_list
#(p,d,q)リスト候補の作成
pdq = list(itertools.product(p, d, q))
pdq = get_unique_list(pdq)
#(sp,sd,sq)リスト候補の作成
seasonal_pdq = [(x[0], x[1], x[2], s) for x in list(itertools.product(sp, sd, sq))]
seasonal_pdq = get_unique_list(seasonal_pdq)
parameters = []
BICs = np.array([])
for param in pdq:
print(param)
for param_seasonal in seasonal_pdq:
print(param_seasonal)
try:
# SARIMAモデルの実装
results = sm.tsa.statespace.SARIMAX(DATA,order=param,seasonal_order=param_seasonal).fit()
# BICが最小値のpが最適なものになります※別途BICは記事にしようと思います
parameters.append([param, param_seasonal, results.bic])
BICs = np.append(BICs,results.bic)
except:
continue
order_df = pd.DataFrame(parameters,columns=["pdq","season_param","BIC"])
order_df = order_df.sort_values("BIC")
#order_dfは昇順のため、order_df.head(1)で最小のパラメータが分かります
return order_df
最適パラメータを探索した結果は以下のようになりました。
- (p,d,q) = (3,1,2)
- (sp, sd,sq,s) = (1,1,1,7)
これらのパラメータを使って、2017年のデータを予測します。
# SARIMAモデルによる予測
SARIMA_target = sm.tsa.statespace.SARIMAX(df_target,order=(3, 1, 2),seasonal_order=(1, 1, 1, 7)).fit()
pred = SARIMA_target.predict("2017-01-01", "2017-12-31")
#テストデータdf_test
df_test = df_company1[["order_date","product_name","quantity"]]
df_test = df_test.query('product_name == "product 1"')
df_test = df_test.query("('2017-01-01' <= order_date) & (order_date <= '2017-12-31')")
df_test = df_test[["order_date","quantity"]]
#グラフの描画
fig,ax = plt.subplots()
ax.plot(pred.index,df_test["quantity"],color="b",label="actual")
ax.plot(pred,color="r",label="pred")
ax.legend()
ax.set_ylabel("quantity")
ax.set_xlabel("Date")
plt.show()
SARIMA実装結果
2017年の原系列と比較すると以下のようになります。
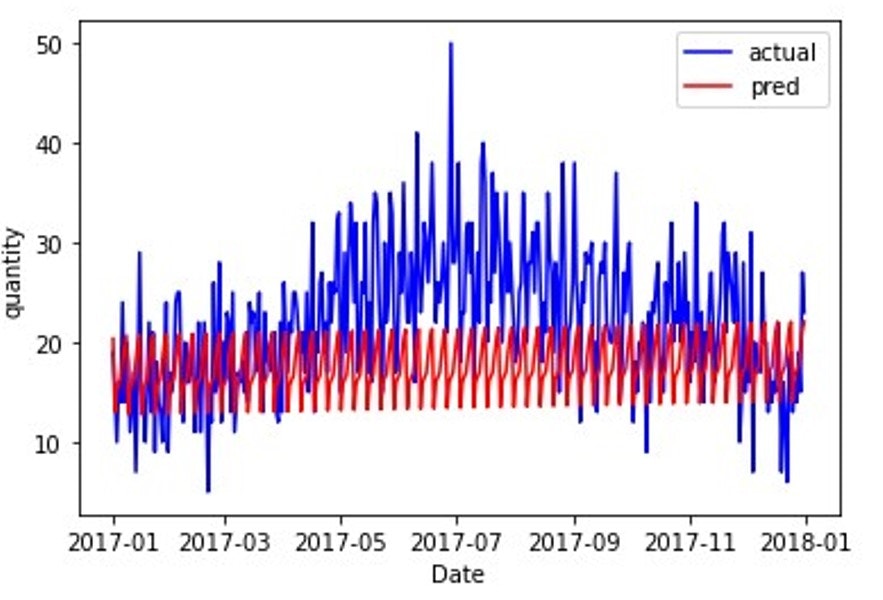
一定の間隔で上下しており、若干増加しているようにも見えますがトレンドを評価できていません。今回は周期が7にしてしまったことに加え、周期関連のパラメータが小さかったことがトレンドを上手く模擬できなかったことが要因であると考えられます。実際、「本記事のデータセット、および、環境」の節におけるproduct1の原系列のグラフを確認してみると、1年で周期性があることが読み取れます。そこで、364日(= 7(日/週)×52(週/年))として周期を修正し再度SARIMAを実施していきました。しかしながら、SARIMAselectparams.pyを用いて最適パラメータの探索を実施すると、3~4時間経過しても最適パラメータを探索し続けるという自体になりました。このことから、データを数日おきのデータに分割し1年周期を考慮可能なデータに変換することを考えました。但し今回の目的は1日毎の需要量の精度向上ではなく、全体の需要量の精度向上であるため、データの個数としては数日おきにするが、需要量は数日分の合計で考慮することにしました。具体的には以下のように数日おきのデータに変換しました。
df_test = pd.DataFrame(columns=[["order_date","quantity"]])
sum_quantity = df_target.iloc[0,1]
for i in range(len(df_target)) :
if i % 7 == 0 : #7日毎のデータにする
df_test = df_test.append({'order_date' : df_target.iloc[i,0], 'quantity' : sum_quantity},ignore_index=True)
sum_quantity = 0
else :
sum_quantity += df_target.iloc[i,1] #7日分の合計需要量の算出
#df_test = df_test[["order_date","quantity"]]
1年周期のため、 s = 52としSARIMAselectparams.pyを用いて最適パラメータを探索した結果は以下のようになりました。
- (p,d,q) = (1,1,2)
- (sp, sd,sq,s) = (0,2,1,52)
適用した予測と原系列の比較結果は以下の通りです(この図を、SARIMA_predと呼ぶことにします)。なお、周期が7のときも同様の比較可能なデータフレームを作成しました。
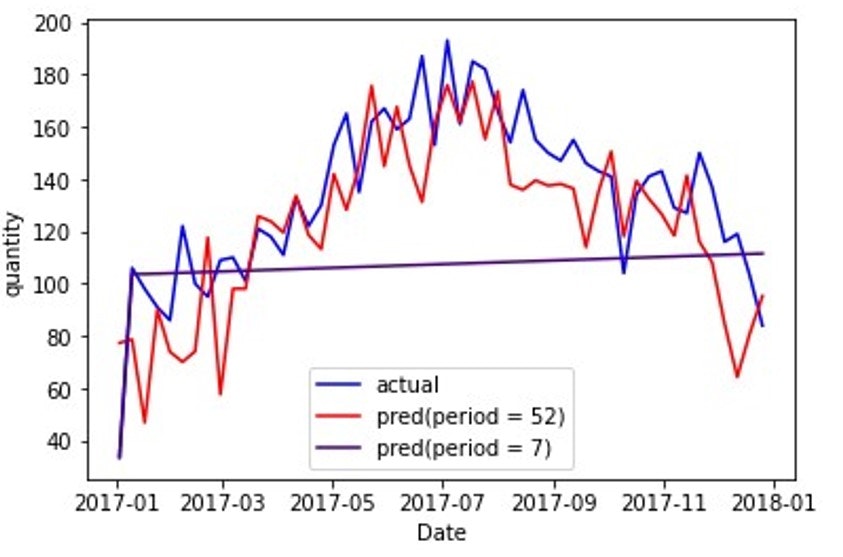
その結果、周期が7日の場合(紫色の線)より周期が1年の場合(赤色の線)の方が、精度の高い予測値が得られていることが読み取れます。このことから、原系列に応じた周期性やトレンドを組み込みやすいデータにすることにより、SARIMAモデルでは精度が向上しやすいことが分かります。しかしながら、需要の差が大きい場合もあることが読み取れ、周期性やトレンドが上手く学習できていない点があることも分かります。
LSTMの適用
LSTMは、Long-Short Term Memoryの略で時系列データに対してニューラルネットワークの考えを適用した手法です。
機械学習は与えられたデータから有益な表現を導出し予測値の精度向上させていきます。ニューラルネットワークはこの有益な表現を導出する際に学習するための層を重ね合わせることで、より有益な表現を導出しようとする手法になります。ただし、時系列データに対してニューラルネットワークを用いると上手くいかない可能性があります。それは時間の経過に応じて動く時系列データの情報に対してニューラルネットワークでは学習が困難であることが要因です。それを解消した手法がLSTMとなります。具体的なLSTMの構造については以下のurlを参考にして下さい(参考url①、参考url②)。
LSTMの訓練データ作成にあたり、まず分析項目を抽出した上で同項目で次元を増やす必要があります。具体的には以下のように実装します。
#訓練データ・テストデータの分割
def split_train_test(data, train_rate):
# データのtrain_rate分を訓練用データとし、残りをテスト用データとする
row = round(train_rate * data.shape[0])
train = data[:row]
test = data[row:]
return train, test
#2016年までのデータ
df_target = df_target[["order_date","quantity"]]
df_target = df_target.query("order_date <= '2016-12-31'")
# 受注項目の次元増加
data = df_target["quantity"]
quantity_data = np.expand_dims(data, 1)
#訓練データ・テストデータ作成
train, test = split_train_test(quantity_data, 0.795)
LSTMを用いる際データのスケールを調整することにより学習効率を改善することがあります。データを一定のルールで扱いやすく変形することを正規化といい、以下のように実装できます。
# データの正規化
scaler = StandardScaler()
train = scaler.fit_transform(train)
test = scaler.transform(test)
LSTM適用にあたり、所定の過去データから翌日のデータを予測していきます。今回を例にしていうと、周期が7(日)であることを利用し、7日毎に分割するデータを作成します。なお、データリスト上では翌日分のデータを考慮して「+1」しています。
!pip install keras #kerasインストール
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
from sklearn.preprocessing import StandardScaler
# window_sizeに分けて時系列データのデータセットを作成
def apply_window(data, window_size):
# データをwindow_sizeごとに分割
sequence_length = window_size
window_data = []
for index in range(len(data) - window_size):
window = data[index: index + sequence_length]
window_data.append(window)
return np.array(window_data)
# 7日毎のデータ作成
window_size = 7
train = apply_window(train, window_size + 1)
test = apply_window(test, window_size + 1)
# 訓練用の入力データ
X_train = train[:, :-1]
# 訓練用の正解ラベル
y_train = train[:, -1]
# テスト用の入力データ
X_test = test[:, :-1]
# テスト用の正解ラベル
y_test = test[:, -1]
LSTMの実装・モデル構築
ニューラルネットワークは層の重ね合わせで学習していくものでした。LSTMの層は以下のように実装できます。
# 入力データの形式を取得
input_size = X_train.shape[1:]
# レイヤーを定義
model = keras.Sequential()
model.add(layers.LSTM(
input_shape=input_size,
units=units,
dropout = dropout,
return_sequences=False,)) #LSTM層をまだ重ねる場合は"True"にする
#入力層 複数重ねるのも可能
model.add(layers.Dense(units=1)) #unitは出力層のユニット数
#モデル生成
model.compile(loss='mse', optimizer='adam', metrics=['mean_squared_error'])
model.fit(X_train, y_train,
epochs=30, validation_split=0.2, verbose=2, shuffle=False)
今回は以下の層の組み合わせで予測値を取得しました。
def train_model(X_train, y_train, units=7, dropout = 0.05):
# 入力データの形式を取得
input_size = X_train.shape[1:]
# レイヤーを定義
model = keras.Sequential()
model.add(layers.LSTM(
input_shape=input_size,
units=units,
dropout = dropout,
return_sequences=True,))
model.add(layers.LSTM(
input_shape=input_size,
units=units,
dropout = dropout,
return_sequences=True,))
model.add(layers.LSTM(
input_shape=input_size,
units=units,
dropout = dropout,
return_sequences=False,))
model.add(layers.Dense(units=2))
model.add(layers.Dense(units=2))
model.add(layers.Dense(units=2))
model.add(layers.Dense(units=1))
model.add(layers.Dense(units=1))
model.compile(loss='mse', optimizer='adam', metrics=['mean_squared_error'])
model.fit(X_train, y_train,
epochs=30, validation_split=0.205, verbose=2, shuffle=False)
return model
#予測値取得関数
def predict(data, model):
pred = model.predict(data,verbose=0)
return pred.flatten()
# 学習モデルを取得
model = train_model(X_train, y_train)
# 検証データで予測
predicted = predict(X_test, model)
#グラフの描画
plt.figure(figsize=(15, 8))
plt.plot(scaler.inverse_transform(y_test),label='actual',color="b")
plt.plot(scaler.inverse_transform(predicted.reshape(-1, 1)),label='pred',color="r")
plt.legend()
plt.show()
LSTM実装結果
2017年の原系列と比較すると以下のようになります(この図を、LSTM_predと呼ぶことにします)。
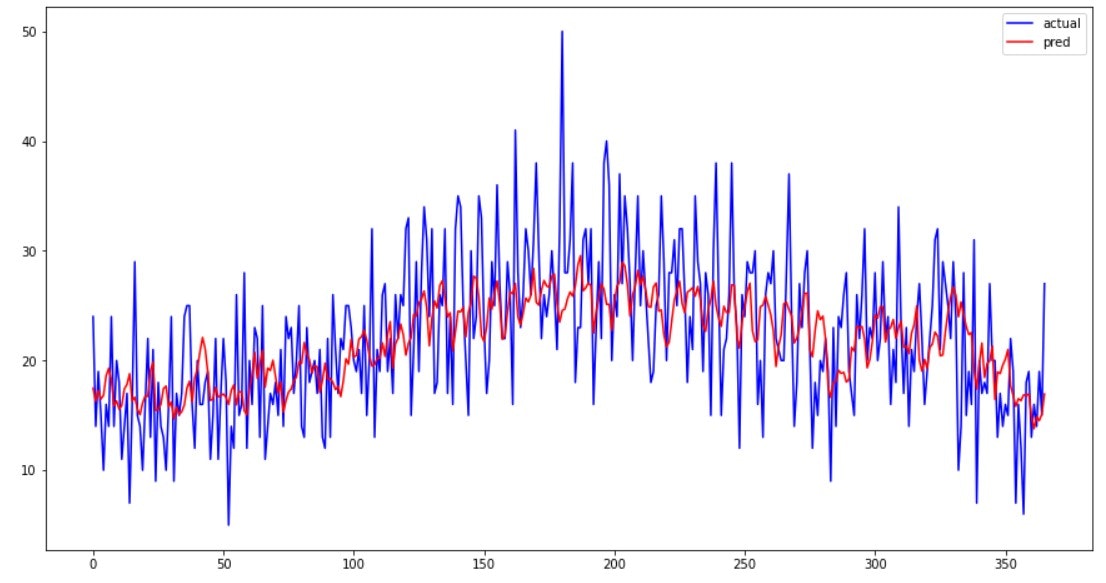
SARIMAの実行結果と比較して、日々の需要変動を表現ができているように見えます。また開発時間の観点では、パラメータ設定の候補を探索時間を考えると、SARIMAはモデル実装までに準備(p,d,qの候補を決めるための処理等)する必要があり、時系列データに応じた構築時間がかかる一方で、LSTMは同一層を重ね合わせるという考えであれば、ある程度開発時間が減少可能かと考えられます。但し、複雑な時系列データになった際は同一層の重ね合わせでは表現が困難であると考えられるので、開発工数を多く見積もった方が良いと思います。
NeuralProphetの適用
NeuralProphetはFacebookが公開しているライブラリで、ProphetとAR-Netという自己回帰型のニューラルネットワークモデルを基にした時系列データ予測モデルです。Prohetでは時系列データは、トレンド、季節変化、休日効果、誤差の4つから成り立つと考えおり、パラメータ設定で簡単にトレンドや周期性を考慮できるモデルとなっています。例えば、下記のようなパラメータがあります。
- トレンドの変化点や変化幅を指定するパラメータ : changepoints_range、n_changepoints
- トレンドの変化幅の制限をするパラメータ : trend_reg
- 周期性を指定するパラメータ : yearly_seasonality(年次周期)、weekly_seasonality(週次周期)、daily_seasonality(日次周期)
- 周期性の変動に対する適合度合いを示すパラメータ : seasonality_reg
- 周期性のモデルパラメータ : seaonality_mode(additive(加法) と multiplicative(乗法))
これらのパラメータを個別に指定することでトレンド・周期性を考慮したモデル構築を簡単にできます。
NeuralProphetは時刻の項目を"ds"、学習項目を"y"で設定する必要があるので、データフレームを以下のように変更します。
#2016年までのデータを訓練データとして、2017年の予測値と比較
df_target = df_company1.query('product_name == "product 1"')
df_target = df_target[["order_date","quantity"]]
df_target = df_target.query("order_date <= '2016-12-31'")
#時刻項目を"ds"、学習項目を"y"に変換
data = df_target.rename(columns={'order_date': 'ds', 'quantity' : 'y'})
周期性は"〇〇_seasonality"パラメータで指定可能です。これは季節性フーリエを用いる方法であり数値を変換することにより早い周期のサイクルに対応できるようです。したがって、TrueかFalseの選択以外に数値での指定が可能ですが、TrueかFalseの指定のみでも十分な精度を出力できます。また、"seasonality_reg"を「0.1~1」で指定することで周期の変動に対してより柔軟に対応可能です。
また、トレンドは変化点・変化幅を考慮するパラメータで指定可能です。例えば、"changepoints_range"は最後から何%のデータをトレンドを予測する際に使用するかを示すパラメータでデフォルトは0.8(80%をトレンド予測に使用するという意味)です。
では実際に最適パラメータを探索してみます。
NeuralProphetの最適パラメータの設定方法とモデル構築
本記事ではoptunaを用いて最適パラメータを探索します。まずはoptunaのインストールを行います。
!pip install optuna
探索方法はこのurlを参考にしました。
from neuralprophet import NeuralProphet
from sklearn.metrics import mean_absolute_error
def objective_variable(train,valid):
#パラメータ設定
def objective(trial):
params = {
'changepoints_range' : trial.suggest_discrete_uniform('changepoints_range',0.8,0.95,0.01),
'n_changepoints' : trial.suggest_int('n_changepoints',50,65),
'trend_reg' : trial.suggest_discrete_uniform('trend_reg',0,2,0.01),
'seasonality_reg' : trial.suggest_discrete_uniform('seasonality_reg',0,1,0.2),
'seasonality_mode' : trial.suggest_categorical('seasonality_mode',['additive','multiplicative'])
}
#パラメータ適用によるモデル
m=NeuralProphet(
changepoints_range = params['changepoints_range'],
n_changepoints=params['n_changepoints'],
trend_reg = params['trend_reg'],],
yearly_seasonality = True,
weekly_seasonality = True,
daily_seasonality = False,
seasonality_reg = params['seasonality_reg'],
epochs = None,
batch_size = None,
seasonality_mode=params['seasonality_mode'])
#モデル予測
future = m.make_future_dataframe(train,periods=len(valid))
forcast = m.predict(future)
#MAE
train_y = train['y'][-len(valid):]
forcast_y = forcast['yhat1']
MAE = mean_absolute_error(train_y,forcast_y)
return MAE
return objective
上記パラメータの最適値を求めるのは以下の通りです。
#パラメータの最適値探索
def optuna_parameter(train,valid):
study = optuna.create_study(sampler=optuna.samplers.RandomSampler(seed=42))
study.optimize(objective_variable(train,valid), timeout=2400)
optuna_best_params = study.best_params
return study
上記のコードで探索したパラメータ結果は以下の通りです。
- (changepoints_range, n_changepoints) = (0.92,64)
- (trend_reg) = (0.63)
- (seasonality_reg) = (0.0)
- (seaonality_mode) = "additive"
これらのパラメータを使って、2017年のデータを予測します。
# NeuralProphetによる予測
m = NeuralProphet(
changepoints_range = study.best_params['changepoints_range'],
n_changepoints = study.best_params['n_changepoints'],
trend_reg = study.best_params['trend_reg'],
yearly_seasonality = True,
weekly_seasonality = True,
daily_seasonality = False,
seasonality_reg = study.best_params['seasonality_reg'],
epochs = None,
batch_size = None,
seasonality_mode = study.best_params['seasonality_mode'])
#訓練データと検証データ
train = data[data['ds'] <= '2016-12-31']
valid = data[(data['ds'] >= '2017-01-01')&(data['ds'] <= '2017-12-31')]
#モデル適用
metric = m.fit(train,freq="D")
future = m.make_future_dataframe(train, periods=365)
forecast = m.predict(future)
pred = forecast[['ds','yhat1']]
#グラフの描画
fig,ax = plt.subplots()
ax.plot(pred["ds"],valid["y"],color="b",label="actual")
ax.plot(pred["ds"],pred["yhat1"],color="r",label="pred")
ax.legend()
ax.set_ylabel("quantity")
ax.set_xlabel("Date")
plt.show()
NeuralProphet実装結果
2017年の原系列と比較すると以下のようになります(この図を、NeuralProphet_predと呼ぶことにします)。
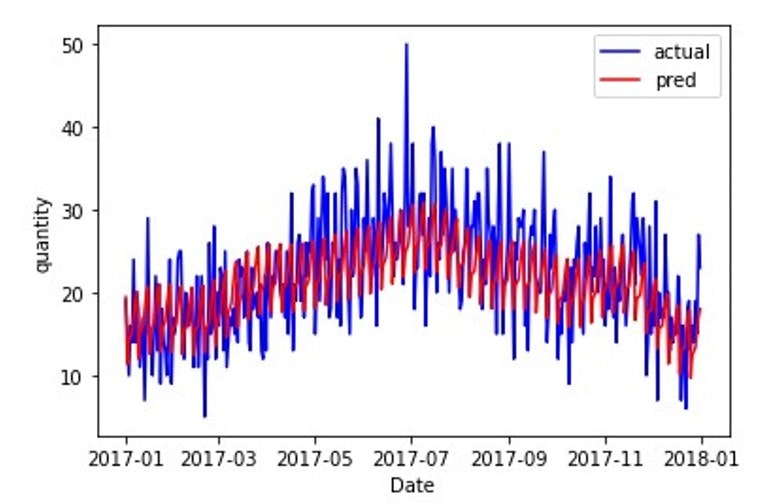
SARIMAと比較すると、LSTMと同様に日々の需要変動を表現できているように見えます。したがって、今回の時系列データではSARIMAモデルよりも良いモデルになったと考えられます。
開発の観点で比較すると、LSTMは前述の通り複雑になれば開発工数が多くなりますが、NeuralProphetはパラメータさえ把握してしまえば、NP_selectparams.pyとNPstudy.pyの組み合わせで可能であるので開発時間は大幅に削減できます。また、今回は最も良い値を得ようと考え、40分(timeout=2400)学習したが、10分程度でも良い結果を導出することはできました。
以上のことから、今回の時系列データに関して、LSTMかNeuralProhetのどちらを適用するべきだと考えられます。そこで、原系列との誤差など定量的な評価も加えて各手法の比較を試みます。
各手法の評価
今回の評価は以下の2点で考えていきます。
- モデルの実装のしやすさ : 実際のコーディング時間だけでなく、モデル構築ためのパラメータの探索時間、結果を受けてのモデルの変に伴う困難さ等結果に至るまでの過程を考慮し、主観のみにならないように、実装して分かったメリット・デメリットも記載
- 原系列との誤差 : 原系列と予測値の誤差、今回はMAE(数式と実装方法例)を使用
まずモデルの実装しやすさを評価しました。

続いてMAEを評価します。MAEは"実際のデータと予測値の差の絶対値"の平均になるので、小さいほうが精度の高い評価値です。なお、SARIMA_predの7日周期と1年周期、LSTM_pred、NeuralProphet_predのMAEを比較します。
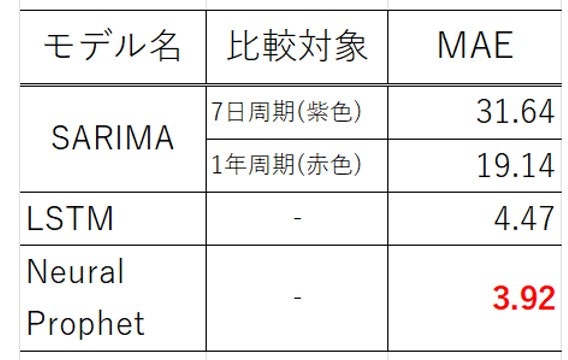
以上より、各手法について以下のようにまとめられます。 - SARIMA : モデル実装のための準備が膨大になる可能性はあるがパラメータと予測値との関係性は把握しやすく、修正箇所の特定はしやすい手法。一方、周期が長いと学習が終わらないのが難点。
- LSTM : 精度向上のための作業は分かりやすく、周期が長くても高い精度が出せる手法。しかし、時系列データが複雑になると開発工数が膨大になる可能性あり。
- Neural Proophet : パラメータさえ理解すれば、短い時間でも高い精度が誰でも出力可能な手法。但しLSTM同様、時系列データが複雑になればパラメータの組み合わせも増えると考えられ、学習時間が増加の可能性あり。
今回の記事のまとめと次の記事の内容(予定)
本記事では、時系列解析の概要と、需要予測における手法のうち、SARIMA、LSTM、NeuralProphetの各手法について実装方法の説明と結果・評価を実施しました。その結果、今回のデータセットにおいて、開発工数と予測精度の両面で、Neuralprophetが良いという結果が得られました。
本記事の動機は開発工数のかからない多品種少量生産下の需要予測手法の確立であり、現在は1品種のみの予測でこのようなの手法とは言えません。そこで、今回のNeuralPprophetの結果を上手く使いつつ重みづけができる手法を確立すればよいとは考えているので、次回はその点に重点を置いた記事を書いていきたいと考えています。
この記事はZennにも公開しています。
色々なブログに挙げてみて、メリット・デメリット勉強したいので。。
参考文献
〇本記事の動機~時系列解析における需要なポイントまで
・ものづくり白書から見る課題。日本の製造業の“課題”と“チャンス”
・需要予測とは?その基本や必要性、目的・具体的な用途を解説
・時系列分析
〇SARIMAの節
・定常時系列の解析に使われるARMAモデル・SARIMAモデルとは?
・【Python】ARモデルで時系列データ分析をやってみる
・【Python】statsmodelsで時系列データの基本的な前処理をやってみる
〇LSTMの節
・LSTMネットワークの概要
・長短期記憶ニューラルネットワークLSTM
・PythonとKerasによるディープラーニング(書籍・Amazon)
〇NeuralProphetの節
・需要予測の各種手法をPythonで実装する
・OptunaでProphetのパラメータをいじって時系列予測の精度を改善してみた
・Prophetでチューニングすべきパラメータ
・Core Module Documentation
・Modelling Seasonality
・Seasonality, Holiday Effects, And Regressors