はじめに
自分自身の知識の整理も兼ねて、需要予測の手法についてPythonで実装・まとめていきたいと思います。
業務上、よく需要予測をしている職場もあると思いますが、ずっと昔から使われていてエクセルで実装できる移動平均のようなクラシックな手法以外にも、最近では機械学習を使った、より高度な手法もあります。
以下ではPythonを使って各種需要予測手法を実装・比較していきます。
需要予測はなぜ重要なのか
サプライチェーンマネジメント(SCM)を考える上で、需要予測は欠かせません。
というのも、多期間における在庫モデルや生産計画を考える上で、需要予測がないと、いつにどれだけ作って、どれだけ在庫を持っておくべきかというような最適化問題を解くことができないからです。
もう少しデメリットについて具体的に言うと、需要予測ができないと在庫の適正化ができず、担当者の感覚に頼って余裕を持って作りすぎて、結果としてCCC(Cash Conversion Cycle:原料仕入れに現金を投入してから最終的に現金化されるまでの日数)が悪化するなどの弊害が生じます。
また、需要予測をしておくことによって、たとえ予測が外れたとしてもハズレた外れた場合のオペレーション計画を事前に立てることもできます。
なので、精度の良し悪しはありますが、需要予測をしっかりしていくことが非常に重要といえます。
今回使用するサンプルデータセット概要
概要
サンプルのデータセットとして、Kaggle のStore Item Demand Forecasting Challengeのデータを使って販売実績を予測(需要予測)していきます。
このデータでは10店舗ある小売店のそれぞれで50種類の商品を売っており、各商品について2013/1/1〜2017/12/31までの日付ごとの販売実績(913000行)がトランザクションデータとしてあります。以下にサンプルを示します。
Salesデータの確認
簡単に中身を確認してみます。
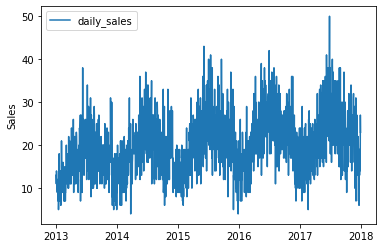
今回はある1つの店舗、ある1つの商品に絞って2013年から2017年の販売実績の推移を確認してみます。
#データセットの中身を確認。すべてを見るのは大変なので、Store==1、item==1のデータに絞って見てみる。
small_df = df.query('store == "1" & item == "1"')
#matplotlibで可視化する
import matplotlib.pyplot as plt
plt.ylabel("Sales")
plt.plot(small_df["date"], small_df["sales"], label="daily_sales")
plt.legend(loc = 'upper left')
plt.show()
1つの年の中で周期性がありそうです。
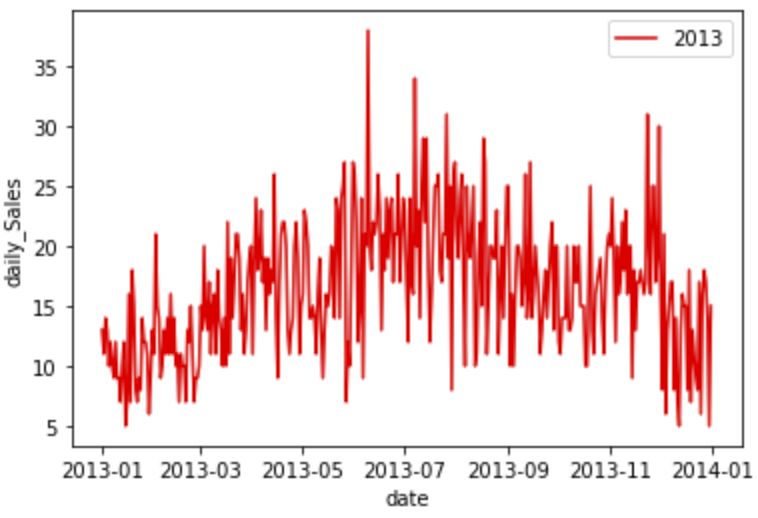
更に区間を狭めて2013年の1年間の販売実績を見てみようと思います。
#2013年に絞ってデータを確認
small_df_1 = small_df.query('year == "2013"')
#matplotlibで可視化する
plt.plot(small_df_1["date"],small_df_1["sales"], color ="red",label = '2013')
plt.ylabel("daily_Sales")
plt.xlabel("date")
plt.legend(loc = 'upper right')
plt.show()
可視化結果は以下です。
どうやらこの商品は季節性があり、6〜8月によく売れているようです。
今回は50製品のうち1製品だけに着目しましたが、他の製品についても同様に確認することができます。
需要予測の各種手法
以下では代表的な手法を用いてサンプルデータセットについて需要予測をしていきます。
移動平均法
移動平均法は過去の売上から算出される移動平均をもとに需要予測をする単純な方法です。
この手法ではスパイクになっている急激な需要変動を予測することはできませんが、季節ごとの大まかな需要変動のトレンドを捉えることができます。
一般的には移動平均を使った需要予測は昨年の販売実績データの移動平均値を使って今年の需要を予測します。
まずは2013年の販売実績について移動平均を求めてみます。
#Store==1、item==1、year==2013のデータに絞る。
small_df = df.query('store == "1" & item == "1" & year =="2013')
#今回は前3日間の移動平均をとったデータをデータセットに追加して生データと比較する。
small_df["rolling_mean_3"] = small_df["sales"].rolling(window = 3).mean()
#可視化
plt.plot(small_df["date"],small_df["sales"], color ="red",label = 'row_data')
plt.plot(small_df["date"],small_df["rolling_mean_3"], color ="blue",label = 'rolling_mean')
plt.ylabel("daily_Sales")
plt.xlabel("date")
plt.legend(loc = 'upper right')
plt.show()
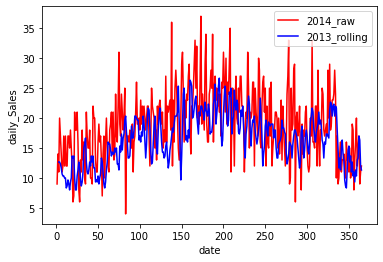
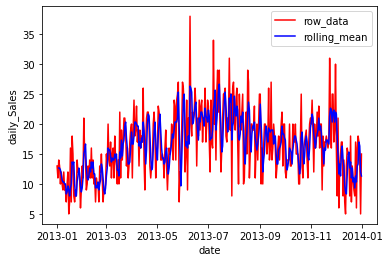
求めた2013年のStore1, item1の移動平均と販売実績(Sales)を比較すると以下のようになります。
ギザギザになっている販売実績の変動が均されるような形に移動平均がなっていることがわかります(青線)。
では次に2013年の移動平均結果を使って、2014の販売実績と比較して見ます。
#2013年と2014年のstore=1, item=1に絞る
small_df = df.query('store == "1" & item == "1"& year =="2013"')
small_df2 = df.query('store == "1" & item == "1"& year =="2014"')
#日付列の追加
days = [i for i in range(1,366)]
small_df["days"]=days
small_df2["days"]=days
#移動平均を計算・列に追加
small_df["rolling_mean_3"] = small_df["sales"].rolling(window = 3).mean()
small_df2["rolling_mean_3"] = small_df2["sales"].rolling(window = 3).mean()
#可視化
plt.plot(small_df2["days"],small_df2["sales"], color ="red",label = '2014_raw')
plt.plot(small_df["days"],small_df["rolling_mean_3"], color ="blue",label = '2013_rolling')
plt.ylabel("daily_Sales")
plt.xlabel("date")
plt.legend(loc = 'upper right')
plt.show()
#MAEで精度の確認
small_df = small_df.dropna()#window=3の移動平均なので最初2つの行はNaNになっている
from sklearn.metrics import mean_absolute_error
print(mean_absolute_error(small_df2['sales'][2:], small_df['rolling_mean_3'])) #4.992653810835629
以下に可視化の結果を示します。
2013年の移動平均結果と2014年の販売実績を比較すると多少の需要の変化はありますが、概ね季節変動を捉えてられており、2013年実績の移動平均をもとに2014年の需要を想定することができることがわかります。
加重移動平均法
加重移動平均法は最新の需要変動の影響に重み付けする手法で、移動平均を取る際に荷重係数を掛け合わせることによって求められます。
直前の変動の影響が大きい(例えば連休やイベント)ような製品の需要予測ではこちらのほうが移動平均よりも精度がよくなることがあります。
加重移動平均(WMA:Weighted Moving Average)を求めるのにはTA-Libというチャート分析用ライブラリを使います。
先程定義したsmall_dfとsmall_df2を使ってやっていきます。
#ライブラリのインポート
import talib
#データの前準備
date = small_df["date"]
small_df.drop('date', axis=1, inplace=True)
small_df = small_df.astype("float64")
#加重移動平均の算出
small_df["wma_3"]=talib.WMA(small_df["sales"].values, timeperiod=3)
#可視化
plt.plot(small_df2["days"],small_df2["sales"], color ="red",label = '2014_raw')
plt.plot(small_df["days"],small_df["wma_3"], color ="blue",label = '2013_wma_3')
plt.ylabel("daily_Sales")
plt.xlabel("date")
plt.legend(loc = 'upper right')
plt.show()
#MAEで精度を確認
from sklearn.metrics import mean_absolute_error
print('MAE(wma):')
print(mean_absolute_error(small_df2['sales'][2:], small_df['wma_3'])) #4.952249770431588
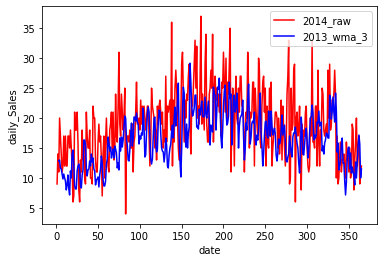
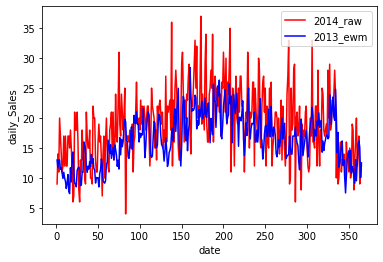
以下に可視化の結果を示します。
先程の移動平均よりもグラフの振動が大きくなっている一方で、MAEも若干ですが加重移動平均のほうが低くなっており、2014年の販売実績と比較するとよりトレンドが一致しているように見えます。
移動平均と加重移動平均は何をしたいかの目的に応じて使い分けると良さそうです。
指数平滑法(EWM:Exponentially weighted method)
重み付けをするという意味では加重移動平均法と近いですが、こちらは指数関数的な重み付けをする手法です。
加重移動平均法のときと同様のデータで比較してみます。
#指数平滑移動平均の算出
small_df["ewm"]=small_df["sales"].ewm(alpha=0.5).mean()
#可視化
plt.plot(small_df2["days"],small_df2["sales"], color ="red",label = '2014_raw')
plt.plot(small_df["days"],small_df["ewm"], color ="blue",label = '2013_ewm')
plt.ylabel("daily_Sales")
plt.xlabel("date")
plt.legend(loc = 'upper right')
plt.show()
#MAEで精度を確認
from sklearn.metrics import mean_absolute_error
print('MAE(ewm):')
print(mean_absolute_error(small_df2['sales'], small_df['ewm'])) #4.811589224904538
以下に可視化の結果を示します。
ぱっと見る限り加重移動平均で求めたものとあまり変わりませんが、大きな違いとして加重移動平均では移動平均を取る区間を自分で設定するのに対して、指数平滑法では平滑パラメーターalphaを調節して目的に合う予測値を出して行きます。
今回のデータでは指数平滑法のほうが移動平均や加重移動平均よりも誤差が小さくなっていますが、扱うデータによって一長一短がありそうですので、目的にあった手法を選ぶことがいいかなと思います。
時系列分析法 (機械学習:NeuralProphet)
これまではクラシックな需要予測の手法を使って直感的にわかりやすい需要予測をしてきました。
一方でこういった手法は人間の直感・経験に頼った処理(例えば移動平均の区間をどうやって取るか)が必要で、使い手によって精度はまちまちになりそうです。
そこでここではFacebookから公開されているNeuralProphetというライブラリを使った機械学習による需要予測を実装してみようと思います。
NeuralProphetは、ProphetとAR-Netという自己回帰型のニューラルネットワークモデルを(Deep Learning)元にした時系列データ予測モデルです。
Deep Learningと聞くと、ブラックボックスで解釈性に乏しいという印象があると思いますが、NeuralProphetは学習後にモデルの捉えたトレンドや周期性の可視化ができ、何をもとに予測されているのかを確認できるため、比較的結果の解釈がしやすいというのが特徴のライブラリになっています。
学習データとしてstore1,item1について、2013~2016年のSalesデータを用い、2017年の需要予測(Salesの予測)を行います。
#NeuralProphetをインポート
from neuralprophet import NeuralProphet
#データセットの準備
df1 = pd.read_csv("train.csv")
df1 = df1.query('store == "1" & item == "1"')
df1 = df1.drop(["store", "item"], axis=1)
df1 = df1.rename(columns = {"date": "ds", "sales": "y"})
#データセットの分割
train = df1[:-365]#2013-2016年の販売実績
test = df1[-365:]#2017年の販売実績
#機械学習モデルのインストタンス作成
m = NeuralProphet(seasonality_mode='multiplicative')
#validationの設定(3:1)&モデルのトレーニング
metrics = m.fit(train,freq="D")
#作ったモデルで2017年のSalesを予測(trainデータの先365日分を予測)
future = m.make_future_dataframe(train, periods=365)
forecast = m.predict(future)
#予測結果をtestのデータフレームに追加
test["pred"] = forecast["yhat1"].to_list()
#MAEで精度を確認
from sklearn.metrics import mean_absolute_error
print('MAE(NeuralProphet):')
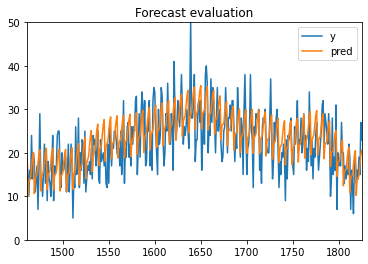
print(mean_absolute_error(test['y'], test['pred']))#3.9889207134508107
#可視化
test.plot(title='Forecast evaluation',ylim=[0,50])
以下に可視化の結果を示します。
得られた予測結果は先程までのクラシックな手法に比べてかなり異なる挙動に見えますが、MAEはかなり改善されました。
過去のデータの単純な需要予測手法に比べてDeep Learningを使ったNeuralProphetが優れていることがわかります。
この予測根拠になったトレンド分析結果をplot_components()とplot_parameters()を使って確認してみます。
fig_comp = m.plot_components(forecast)
fig_param = m.plot_parameters()
こちらの分析結果は予測対象の2017年のトレンドと季節変動をモデルの中で分解した結果です。
なだらかな上昇傾向と年間の季節変動、1週間の間の季節変動が自動的に算出されていることがわかります。
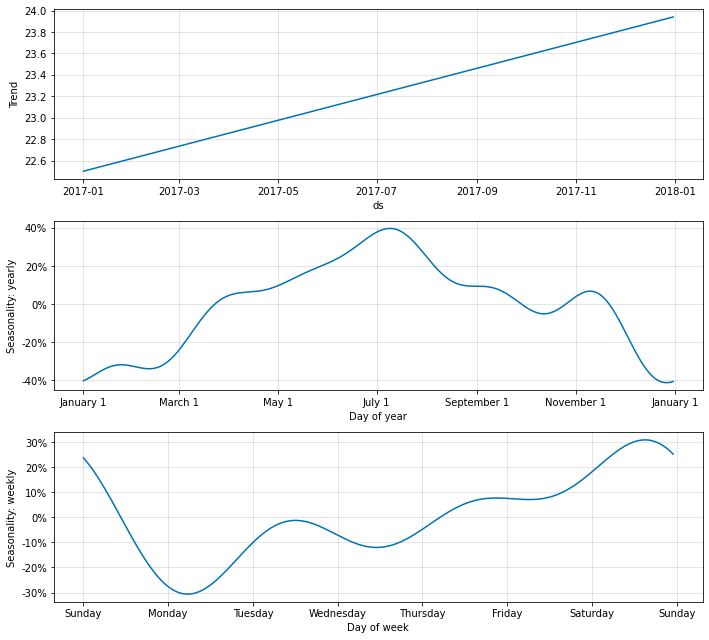
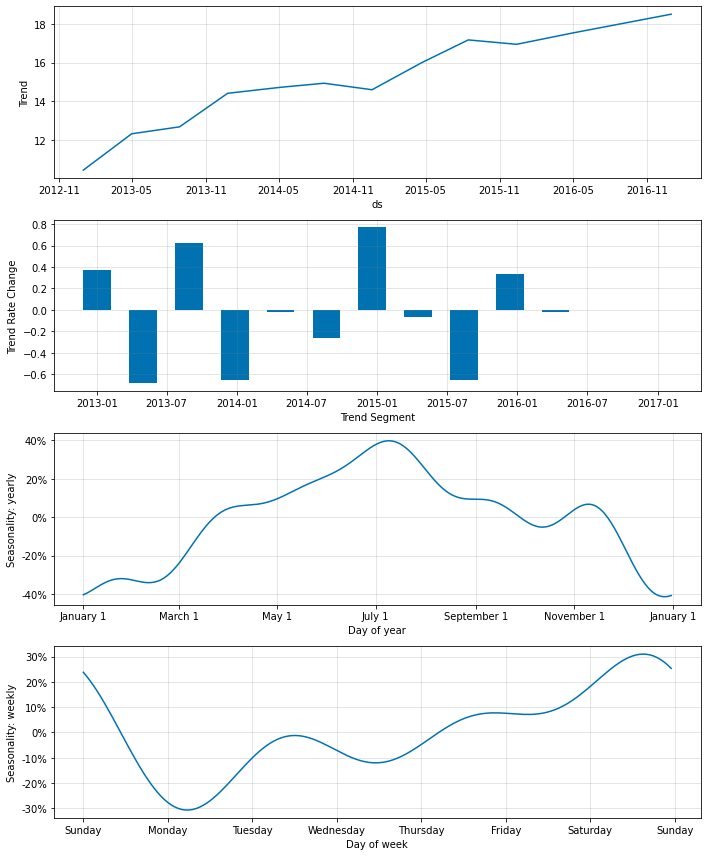
以下の2つ目のグラフは学習データの分析データです。
数年間のトレンドの上昇傾向、各年の時期ごとでの変動率等の情報が出力されています。
これらのデータを見ることで、おおよその過去の傾向のsummaryがわかり、かつ予測結果が何から導かれているのかが理解できます。
その他の需要予測方法
今回は長くなりましたので詳細を割愛しますが(作るときは別記事にします)、需要予測の方法として複数の説明変数からSalesを予測するというまた別のアプローチがあります。
これまでの需要予測はすべて過去のSalesデータと時系列情報のみを使った予測でしたが、それは様々な外的な要因の結果系しか見てない予測になります。
例えば、夏季に需要が高くなる商品や雨季に需要が高まる商品があったとして、それは例えばアイスだったり傘だったりします。
それらは天気や気温によってかなり売れ行きが変わることが簡単に想像できると思います。
Salesデータと時系列の情報にはそういった影響度が高いと思われる細かい情報(説明変数)が欠落しているので予測できる精度にも限界があります。
なので、データとして天気や気温、購入日時、購入者の性別、周辺地域でのイベントの有無などが販売実績と一緒に記録されているようなデータセットであればそれらを説明変数としてPLSなどの回帰モデルや勾配Boostingなどの非線形回帰モデルを使って需要予測をすることができます(Salesデータは説明変数として使用しない)。
おわりに
需要予測について様々な手法を見てきました。
SCMにおける需要予測の重要性については最初にお伝えしたとおりですが、一方で需要予測は万能ではありません。
COVID-19のパンデミックによって既存の需要予測はほとんど当てにならないものになったという話を聞きました。
それは上記で紹介した技術すべてに共通しているのですが、パンデミックや戦争のような人生で1度きりみたいな大きく不連続な変化を過去のデータから予測することは難しいからです。
ですので、需要予測するにあたっては、その要素が何で、どんな前提に基づいた予測なのかを知っておくことが重要です。
そうすれば、需要予測が外れ始めたときに何が原因なのか、どうすればいいのか(場合によっては需要予測のモデルを使わないという選択をする)について考える指針になると思いますので、本記事がその参考になれば幸いです。
参考文献
- 需要予測で在庫管理を効率化!計算式や精度を上げる方法を紹介
- Python言語によるサプライ・チェイン・アナリティクス
- 【需要予測の手法】製造業における在庫管理の改善・在庫削減に活かす
- Machine Learning for Retail Demand Forecasting
- 【FX,Python】PythonとTA-Libで加重移動平均(WMA)を引く
- Mac OSでTA-Libをpipで入れられなかった時の対処法
- Pythonでサクッと作れる時系列の予測モデルNeuralProphet(≒FacebookのProphet × Deep Learning)
- NeuralProphetで時系列データ予測
- NeuralProphet公式
- A-Forecastによる需要予測(基礎編)