index
主成分分析(PCA)とは
- 全体をわかりやすく見通しの良い1~3程度の次元に要約していくこと。
- ビッグデータは多変量、多次元であるためそのままでは理解しにくいが、主成分分析を行うことにより、データの持つ情報をできる限り損なわず、かつデータ全体の雰囲気を可視化し、誰もが理解しやすい形にすることが可能。
以下はWikipediaから抜粋
主成分分析(しゅせいぶんぶんせき、英: principal component analysis; PCA)は、相関のある多数の変数から相関のない少数で全体のばらつきを最もよく表す主成分と呼ばれる変数を合成する多変量解析の一手法[1]。データの次元を削減するために用いられる。
主成分を与える変換は、第一主成分の分散を最大化し、続く主成分はそれまでに決定した主成分と直交するという拘束条件の下で分散を最大化するようにして選ばれる。主成分の分散を最大化することは、観測値の変化に対する説明能力を可能な限り主成分に持たせる目的で行われる。選ばれた主成分は互いに直交し、与えられた観測値のセットを線型結合として表すことができる。言い換えると、主成分は観測値のセットの直交基底となっている。主成分ベクトルの直交性は、主成分ベクトルが共分散行列(あるいは相関行列)の固有ベクトルになっており、共分散行列が実対称行列であることから導かれる。
主成分分析を試す
以下のプログラムは、RandomStateオブジェクトを使って、2変数のデータセットを生成し、各変数について標準化したものをプロットしたもの。
from sklearn.preprocessing import StandardScaler
# np.Random.RandomState(1)としてシード(乱数の初期値)を1に設定したRandomStateオブジェクトを作成
sample = np.random.RandomState(1)
# rand関数とrandn関数を使って、2つの乱数を生成
X = np.dot(sample.rand(2, 2), sample.randn(2, 200)).T
# 標準化
sc = StandardScaler()
X_std = sc.fit_transform(X)
# 相関係数の算出とグラフ化
print('相関係数{:.3f}:'.format(sp.stats.pearsonr(X_std[:, 0], X_std[:, 1])[0]))
plt.scatter(X_std[:, 0], X_std[:, 1])
以下が出力結果
相関係数0.889:

標準化の部分の参考URL
主成分分析の実行
主成分分析はsklearn.decompositionモジュールのPCAクラスを使うと実行できる。
オブジェクトの初期化の際、変数を何次元まで圧縮したいか、つまり、抽出したい主成分の数をn_componentsとして指定する。
通常は元ある変数よりも小さい値を設定する。(30変数を5変数に減らすなど)
fitメソッドを実行することで、主成分の抽出に必要な情報が学習される。(具合的には、固有値と固有ベクトルが計算される)
# インポート
from sklearn.decomposition import PCA
# 主成分分析
pca = PCA(n_components=2)
pca.fit(X_std)
PCA(copy=True, iterated_power='auto', n_components=2, random_state=None,
svd_solver='auto', tol=0.0, whiten=False)
学習結果の確認
components_属性
components_属性は固有ベクトルと呼ばれるもので、主成分分析により発見された新しい特徴空間の軸の向きを表す。
print(pca.components_)
[[-0.707 -0.707] #第1主成分の向き
[-0.707 0.707]] #第2主成分の向き
explained_variance_属性
explained_variance_属性は各主成分の分散を表します。
print('各主成分の分散:{}'.format(pca.explained_variance_))
各主成分の分散:[1.899 0.111]
今回抽出された2つの主成分の分散が、それぞれ1.889と0.111であることがわかるが、ここで分散の総和が2.0となるのは偶然ではなく、(標準化された)変数が元来有していた分散の総和と、主成分の分散の総和は一致する。つまり、分散(情報)は維持されているということ。
explained_variance_ratio_属性
explained_variance_ratio_属性は、各主成分が持つ分散の比率である。
print('各主成分の分散割合:{}'.format(pca.explained_variance_ratio_))
各主成分の分散割合:[0.945 0.055]
最初の0.945は1.889/(1.889+0.111)によって得られ、第1主成分で元のデータの94.5%の情報を保持しているとわかる。
以上の結果を図式してみる。
# パラメータ設定
arrowprops=dict(arrowstyle='->',
linewidth=2,
shrinkA=0, shrinkB=0)
# 矢印を描くための関数
def draw_vector(v0, v1):
plt.gca().annotate('', v1, v0, arrowprops=arrowprops)
# 元のデータをプロット
plt.scatter(X_std[:, 0], X_std[:, 1], alpha=0.2)
# 主成分分析の2軸を矢印で表示する
for length, vector in zip(pca.explained_variance_, pca.components_):
v = vector * 3 * np.sqrt(length)
draw_vector(pca.mean_, pca.mean_ + v)
# xあるいはyの上限・下限を調整して同じ座標値の増分が同じ長さになるように調整
plt.axis('equal');
以下が出力結果である。
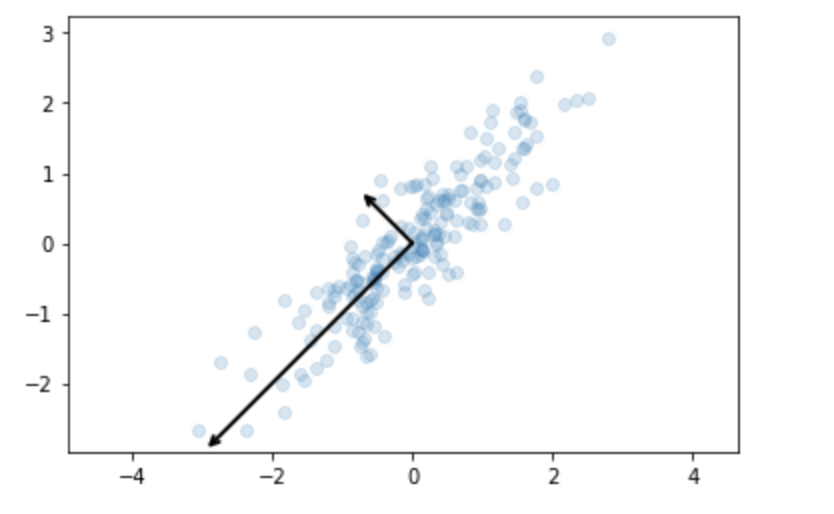
上の矢印が主成分分析によって得られた新しい特徴空間の軸の方向である。
分散が最大の方向に第1主成分が定まり、第2主成分とのベクトルに対して、お互いに直交していることがわかる。
図を見て分かる通り、元の散布図に対して分散が最大になる方向のベクトルが第1主成分、そしてその次に分散が大きい方向のベクトルが第2主成分である。第1主成分と第2主成分は直交する。(直交基底)
主成分分析の実例
ここからは、主成分分析を使って次元を圧縮することがどのような場面で役に立つのか、具体的に見ていく。
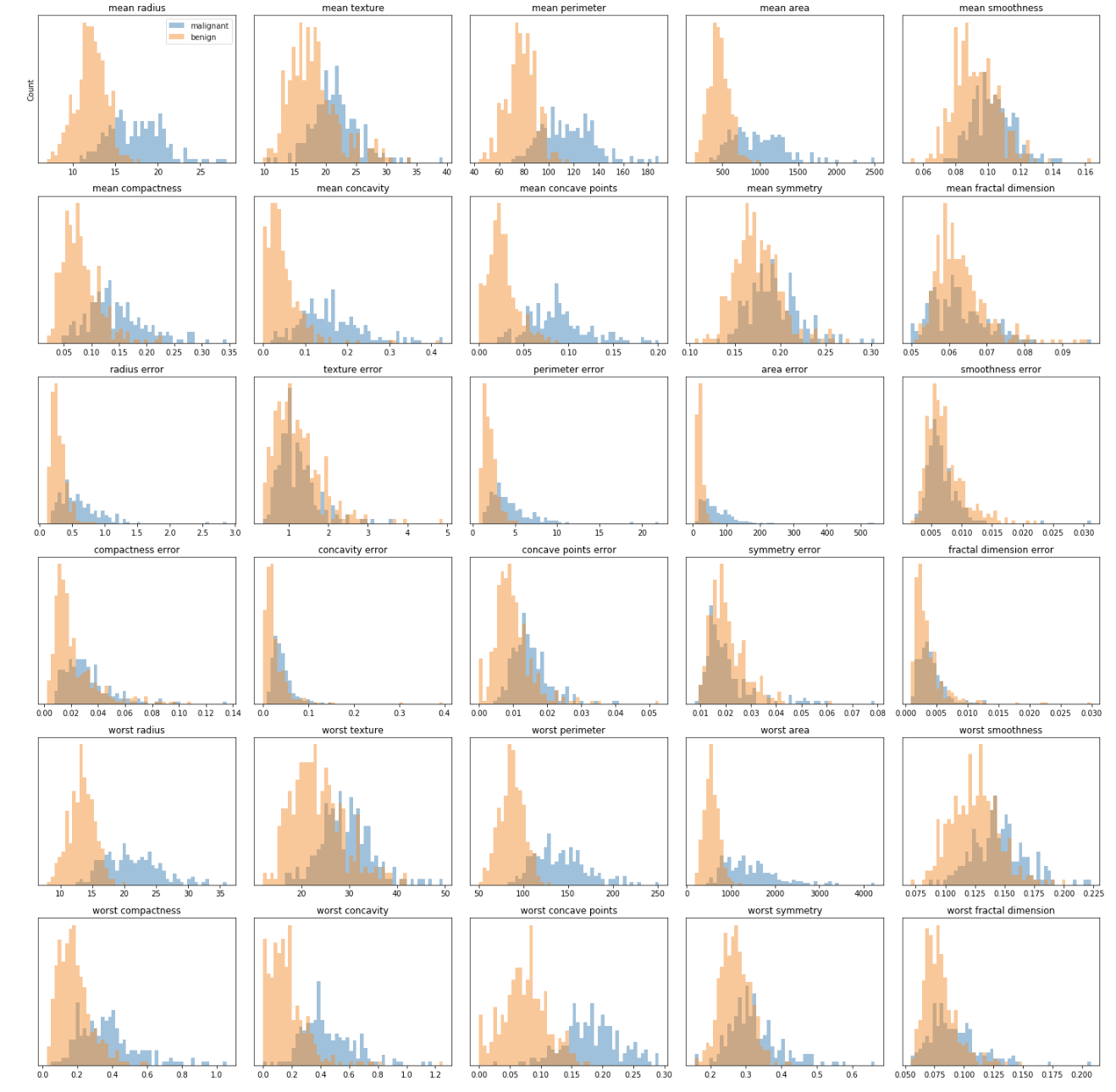
乳がんデータは、sklearn.datasetsのload_breast_cancer関数を使って読み込めます。以下に示すのは、データを実際に読み込み、目的変数(cancer.target)の値が「malignant(悪性)」か「benign(良性)」によって、各説明変数の分布を可視化したもの。
# 乳がんデータを読み込むためのインポート
from sklearn.datasets import load_breast_cancer
# 乳がんデータの取得
cancer = load_breast_cancer()
# データをmalignant(悪性)かbenign(良性)に分けるためのフィルター処理
# malignant(悪性)はcancer.targetが0
malignant = cancer.data[cancer.target==0]
# benign(良性)はcancer.targetが0
benign = cancer.data[cancer.target==1]
# malignant(悪性)がブルー、benign(良性)がオレンジのヒストグラム
# 各図は、各々の説明変数(mean radiusなど)と目的変数との関係を示したヒストグラム
fig, axes = plt.subplots(6,5,figsize=(20,20))
ax = axes.ravel()
for i in range(30):
_,bins = np.histogram(cancer.data[:,i], bins=50)
ax[i].hist(malignant[:,i], bins, alpha=.5)
ax[i].hist(benign[:,i], bins, alpha=.5)
ax[i].set_title(cancer.feature_names[i])
ax[i].set_yticks(())
# ラベルの設定
ax[0].set_ylabel('Count')
ax[0].legend(['malignant','benign'],loc='best')
fig.tight_layout()
ほとんどのヒストグラムについて、malignantとbenignのデータが重なっており、このままだと悪性か良性かを見分けるためにどこに境界線を引いていいのかの判断は厳しい。
ここで主成分分析を使い、これら20以上ある変数の次元を削減してみる。具体的には、説明変数となるデータを標準化し、主成分分析を行う。抽出する主成分の数(n_component)は2とする。
# 標準化
sc = StandardScaler()
X_std = sc.fit_transform(cancer.data)
# 主成分分析
pca = PCA(n_components=2)
pca.fit(X_std)
X_pca = pca.transform(X_std)
# 表示
print('X_pca shape:{}'.format(X_pca.shape))
print('Explained variance ratio:{}'.format(pca.explained_variance_ratio_))
X_pca shape:(569, 2)
Explained variance ratio:[0.443 0.19 ]
以上から、explained_variance_ratio_属性の値を確認すると、変数の数は2つに減るものの、元の情報の約63%(=0.443+0.19)が、第1主成分と第2主成分に凝縮されていることがわかる。
これは出力結果から、「X_pca shape:(569, 2)」は、主成分分析をした後のデータは、569行2列(2変数)になっているところからわかり、2変数は主成分分析の数を2に設定したので、2になっている。
次に、次元を低くしたデータを可視化してみる。まずは可視化準備のため、第1主成分と第2主成分のデータに、説明変数に対応する目的変数を紐付け、そののち良性データと悪性データに分離する。
# 列にラベルをつける、1つ目が第1主成分、2つ目が第2主成分
X_pca = pd.DataFrame(X_pca, columns=['pc1','pc2'])
# 上のデータに、目的変数(cancer.target)を紐づける、横に結合
X_pca = pd.concat([X_pca, pd.DataFrame(cancer.target, columns=['target'])], axis=1)
# 悪性、良性を分ける
pca_malignant = X_pca[X_pca['target']==0]
pca_benign = X_pca[X_pca['target']==1]
# 悪性をプロット(赤色)
ax = pca_malignant.plot.scatter(x='pc1', y='pc2', color='red', label='malignant');
# 良性をプロット(青色)
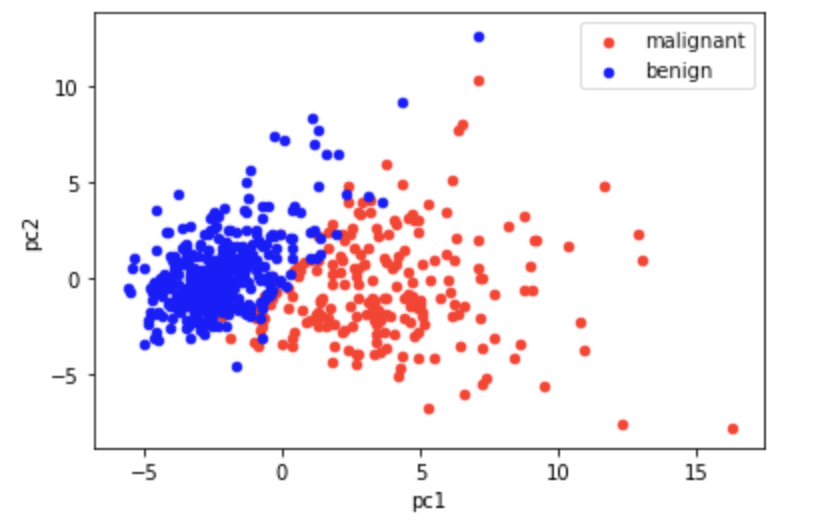
pca_benign.plot.scatter(x='pc1', y='pc2', color='blue', label='benign', ax=ax);
上のグラフをみる限り、本ケースにおいては、わずか2つの主成分で目的変数のクラスをほぼ分離できることがわかる。
変数が多くどの変数を分析に活用すべきかわからない場合などは、このように主成分分析を行い、
(1)各主成分と目的変数の関係を明らかにする
(2)各主成分と元変数の関係から元変数と目的変数の関係を解釈する
などと進めるとデータ理解が進むだろう。
また主成分分析は、予測モデルを構築する際に変数の数を減らしたい場合(次元削減)にも活用できることを覚えておくべき。