主成分分析で「九条カレンのポーズ」から正規直交基底を検出する

やること

九条カレンの通称「正規直交基底のポーズ」から正規直交基底を自動で求めていきたいと思います。

こんな感じ

アルゴリズム

※Numpy, matplotlib, sklearn, PILを使用します

import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from PIL import Image, ImageFilter

1.画像を適当なサイズに縮小して読み込み

軸を求める部分が重いので、小さめの画像にリサイズします。この例では元画像の半分（横幅512px）にリサイズしました。¹

with Image.open("karen.jpg") as img:
    img = img.resize((img.width//2, img.height//2), Image.BICUBIC) # 1/2にリサイズ（メモリ対策）
    original = np.asarray(img, np.float32) / 255.0 # [0, 1]のNumpy配列に

後で使うのでNumpy配列としても保持しておきましょう。

2. エッジ検出

最終的にはこの画像を0,1に変換したいのです（二値化）。これは画像の内容にもよりますが、アニメ画像の場合は軸を求める際に、塗りつぶされた領域よりも輪郭線を見てほしいので、エッジ検出を行ってみました。特徴量を抽出しているイメージです。エッジ検出の前には一度グレースケール化をします。エッジ検出はPILの場合はImageFilter.FIND_EDGESでできます。

with Image.open("karen.jpg") as img:
    img = img.resize((img.width//2, img.height//2), Image.BICUBIC) # 1/2にリサイズ（メモリ対策）
    original = np.asarray(img, np.float32) / 255.0 # [0, 1]のNumpy配列に
    edge = np.asarray(img.convert("L").filter(ImageFilter.FIND_EDGES), np.float32) / 255.0  # エッジ検出しNumpy配列へ

最終的に二値化したいだけなので、別にエッジ検出でなくても良いです。簡単な画像なら、グレースケール化した画像を二値化するのもよいでしょう。

3. 二値化

エッジ検出の結果は0～255のグレースケールになっているので、これを0，1に変換します。

binary = edge >= 0.5 # 2値化

0～1スケールのNumpyの場合、例えば「0.5以上なら1、そうでなければ0」とします。このスレッショルドは変えても構いません。

4.xy座標（yx座標）に変換

今までは「(y, x)の座標に対して輝度が0か1か」というデータ構造でしたが、これを「輝度が1である(y, x)のペア」というデータ構造に変換します。xとyが逆になっているのは、Numpyでの画像の構造が(y, x, ch)だからです（軸を扱う際は注意）。

この処理はnp.whereを使うだけですぐできます。ただし、この関数の出力は(2, 輝度が1のマス数)という次元になるので、転置させます。

pos = np.asarray(np.where(binary)).T.astype(np.float32) # 2値化した白の部分の座標を(y, x)で取る
print(pos.shape) # np.whereの結果が(2, 該当ピクセル数)なので転置している
# (10018, 2)

5. 主成分分析

ここが本体で、「九条カレンのポーズ」の軸を求めるために主成分分析をします。Scikit-learnの関数を使いましょう。

p = PCA(n_components=2) # 主成分分析
p.fit(pos)
eigen = np.asarray(p.components_) # 軸（固有ベクトル）

ここでPCAのcomponent_というオブジェクト（固有ベクトル）が重要で、この固有ベクトルが軸の向きを表します。確認してみましょう。

print(eigen)
print(np.dot(eigen, eigen.T))
print(np.dot(eigen.T, eigen))  # eigenが直交行列になっていることを確認（積が単位行列になっている）

勘の良い方はもう既にわかっているかもしれませんが、固有ベクトルが回転行列のような形になっています（符号は違う）。

[[-0.18205993 -0.98328745]
 [-0.98328745  0.18205993]]
[[1.0000000e+00 1.9925341e-09]
 [1.9925341e-09 1.0000000e+00]]
[[1.0000000e+00 1.9925341e-09]
 [1.9925341e-09 1.0000000e+00]]

これで軸を求めることができました。

転置されたものとの積が単位行列になっているので、この固有ベクトルの行列は直交行列であることが確認できます。これは求められた軸が正規直交基底であるということの裏付けにもなっています。

6. プロットしてみる

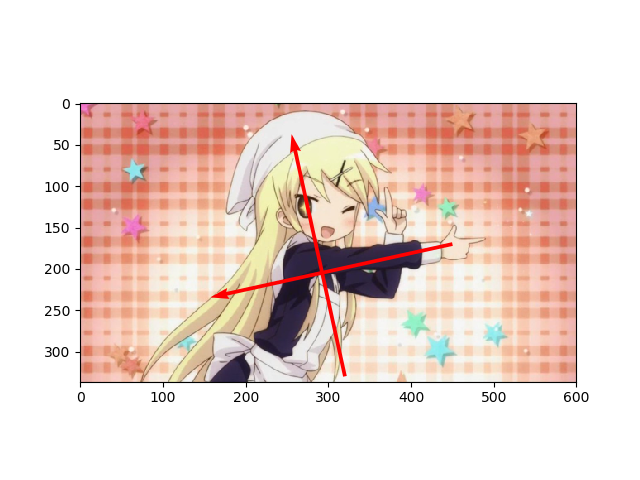
いよいよ求めた「正規直交基底」を九条カレンに重ねてみます。

plt.imshow(original)
plt.quiver([380, 320], [200, 10], eigen[1], eigen[0], color="red", scale=2) # (y, x)なのに注意
plt.show()

わーい！　正規直交基底だ！！

なぜこうなるのか

なぜこのようになるのでしょうか。それは、主成分分析のやっていることが、データにフィットするような軸を探すことだからです。

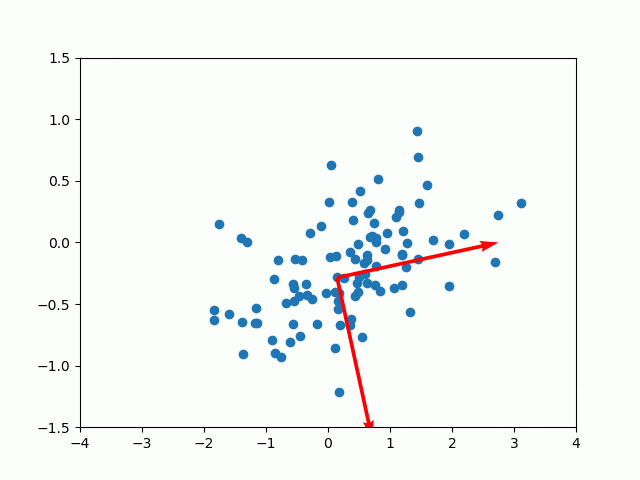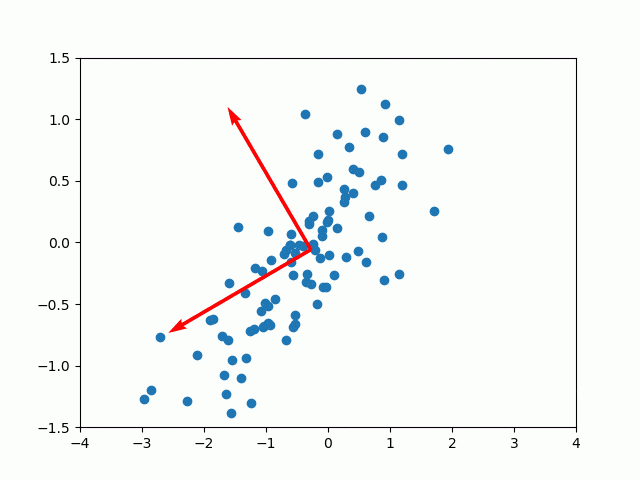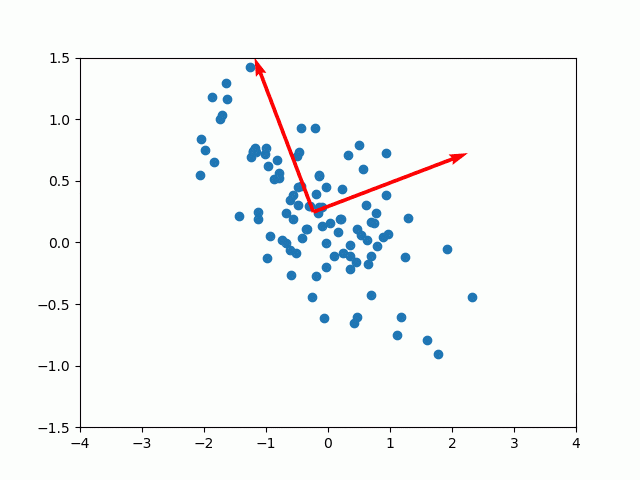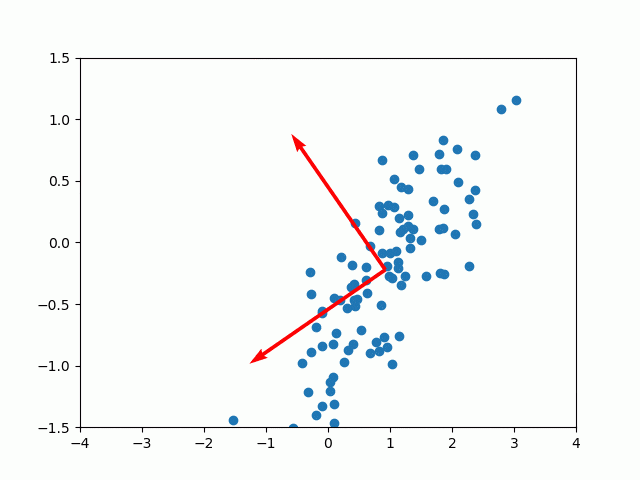
例えばランダムな点に対して、主成分分析で軸を探してみます。

コード（クリックで展開）

import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA

def random_plot():
    # データの作成
    original_data = np.random.randn(100, 2)
    original_data[:, 1] /= 3.0
    theta = np.random.uniform(-np.pi / 5, np.pi / 5)
    rotation = np.array([[np.cos(theta), -np.sin(theta)], [np.sin(theta), np.cos(theta)]])
    projection = np.dot(original_data, rotation)
    transform = np.random.uniform(-1, 1, (1, 2)) * np.array([[1, 0.5]])
    projection = projection + transform
    # PCA
    pca = PCA(n_components=2)
    pca.fit(projection)
    # プロット
    plt.scatter(projection[:, 0], projection[:, 1])
    plt.xlim(-4,4)
    plt.ylim(-1.5, 1.5)
    plt.quiver(transform[0], transform[0].T, pca.components_[:, 0], pca.components_[:, 1], scale=3, color="red")
    plt.show()

綺麗に軸を探すことができました。主成分分析は次元削減のツールとして使われますが、変換後の次元を入力の次元と同じにすれば、元のデータを損なわずに軸だけ探すことができます²。

先程の例では、九条カレンの画像の輪郭をこのような点の集合と捉えることで、軸の検出が可能になります。

応用：回転された画像の修正

簡単な画像かつ微小なブレであれば、この方法を用いて回転された画像を修正することができます。軸の検出がうまく行けば人間による調整はいりません。

考え方は単純です。正規直交基底を求めてから、xy軸とのなす角を計算します。これはnp.arcsinなどの逆三角関数でできます（回転行列を作って逆行列を求めるのも良いです）。修正するための回転角を求めたら、アフィン変換をすれば終わりです。

コードは次のとおりです。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from PIL import Image, ImageFilter

def karen_rotate(degree, idx):
    with Image.open("karen2.jpg") as img:
        img = img.rotate(degree, fillcolor="black", expand=True) # 回転（度数）
        width, height = img.size
        original = np.asarray(img, np.float32) / 255.0 # [0, 1]のNumpy配列に
        edge = np.asarray(img.convert("L"), np.float32) / 255.0
    binary = edge >= 0.05 # 2値化 （エッジ検出はしない、非常に小さいスレッショルドにする）
    pos = np.asarray(np.where(binary)).T.astype(np.float32) # 2値化した白の部分の座標を(y, x)で取る

    # 主成分分析
    p = PCA(n_components=2) # 主成分分析
    p.fit(pos)
    eigen = np.asarray(p.components_) # 固有ベクトル

    # 回転角の計算（とりあえずうまく行った方法なのでもしかしたらうまく行かないことあるかも）
    rotate_degree = np.arcsin(eigen[0, 0]) * 180 / np.pi # 修正角度、np.arcsinはラジアンなので度数に変換
    with Image.fromarray((original * 255).astype(np.uint8)) as img:        
        fixed_img = img.rotate(int(rotate_degree)) # アフィン変換
        fixed_np = np.asarray(fixed_img, np.uint8)

    # 結果のプロット
    ax = plt.subplot(4, 3, 3 * idx + 1)
    ax.imshow(binary)
    ax = plt.subplot(4, 3, 3 * idx + 2)
    ax.imshow(original)
    ax.quiver(np.repeat(width // 2, 2), np.repeat(height // 2, 2), eigen[1], eigen[0], color="red", scale=2)
    ax.set_title("deg = " + str(degree))
    ax = plt.subplot(4, 3, 3 * idx + 3)
    ax.imshow(fixed_np)
    
if __name__ == "__main__":
    plt.subplots_adjust(top=0.92, bottom=0.05, left=0.05, right=0.98)
    for i, d in enumerate([-30, -15, 15, 30]):
        karen_rotate(d, i)
    plt.show()

結果は次のようになります³。

左から、二値化したときの画像、回転済みの画像と主成分、右が回転修正した画像です。どの例も回転された画像がきちんと戻っているのがわかります。

ただし、回転角があまりに大きすぎると（45度以上）、90度反転したような画像が出てくるので注意してください。

コツ

二値化する前の特徴抽出がポイントです。正規直交基底のポーズの場合はエッジ検出をしましたが、回転補正をする場合はエッジ検出をしていません。回転補正をする場合は、メインのエリアを長方形で取り出すなど、できるだけ簡単な画像に変換すると精度が上がります。

また、ポーズから軸の抽出をする場合は、手のポーズと姿勢の主従に注意してください。次のケースのように、手の面積よりも身体の面積のほうが明らかに大きい場合は、姿勢側で軸が検出されうまくいきません。

1. 画像はこちらから　https://togetter.com/li/825944 https://twitter.com/tina_quaver/status/601439736461295619 ↩

2. 逆に言えば、次元削減としての主成分分析は、様々な軸の候補を説明分散でソートし、重要な順に取っているだけということだけです ↩

3. 画像はこちらから　https://togetter.com/li/825944 ↩