統計的推論と、統計的学習(予測)の両面からリサンプリングを説明したい。
コンセプトは「非Rユーザーな初心者でも分かりやすく」。
初めに統計2級程度の「標本抽出や推測(推計)統計学」の話をする。
その後リサンプリング法としてbootstrap法を紹介する。
対象読者:数式なし、高校生レベル、非Rユーザーはコードを無視して読み進めること推奨
前提知識はこの前勉強会で作った資料を参照してほしい。
この記事の続編はこちら
プロローグ『単語の紹介』
データサイエンスの認知も高まり、最近では中学生から「標本抽出」の考えが教科書に入り、高校生では「確率分布と母平均の推定」などが学習項目に入っている。
推測統計とは全体を知る事の出来ない調査対象に対して標本を採ることで、「母集団の性質を解き明かす=推定」ことが目的である。
学生生活で何気なくフィールドワークを通してアンケートや水質調査などを行うだろうが、その実験結果の効力を最大限高めるためにも推測統計を知ってもらいたいと思う。
まずは本文で登場する言葉の意味を記述していく。
- 標本
- 調査対象(推定したい対象,母集団)から実験的に抽出したデータ
- 標本数,サンプル数
- 標本がいくつあるか
- 実験によって解釈が異なるので難しいが、一回の抽出実験を1本とする場合が主
- 例えば同じ地盤から10本土壌サンプルを作ってもこれはサンプル数1本とカウントする
- サンプル数、サンプルサイズ、母数、分母の言葉はビジネスの場でも良く誤用される
- 標本のサイズ,サンプルサイズ
- 標本ひとつあたり何個のデータが入っているか
- 100人の身長を各都道府県でとったならば
- 「サンプルサイズ100の標本数は47」となる
- 標本化
- 母集団から標本を採ってくること
- サンプリングとも呼ぶ
- 再標本化
- 標本をさらに分割し、小集団・小標本にすること
- リサンプリングとも呼ぶ
- 標準偏差
- ばらつきを表す数値、分散の平方根
- 標準誤差
- サンプルの標準偏差を計算したもの
- 母集団
- 今回は推定したい対象であり、母集団
- サイズの小さい母集団ならば全数検査も可能
- 母数,パラメーター
- 母集団の統計量の事(母平均、母分散など)
- よく分母の意味で誤用される
- 母平均
- 母集団の統計量である平均値
- 標本平均
- 標本内の統計量である平均値
- 標本分布
- 標本として抽出したものの分布
- ヒストグラムが分かりやすい
- 標本統計量の分布
- 標本を抽出し、統計量を計算する
- その統計量の分布
- サンプリング分布とも呼ぶ(諸説あり)
- ブートストラップ分布
- ブートストラップ法により再標本化した小集団の統計量の分布
- 本記事ではブートストラップ-サンプリング分布、という単語を使って表示することにする
第一章『1を知り全を知ることはできないのか』
推測したい対象は非常に大きな集団であり、少数のチームでは調査が実行できない場合が多い。
本記事での仮の課題として
課題「日本の20代後半の女性の平均身長を知りたい」
を使ってみようと思う。
(e-stat 2017年を参考にしたが、説明の都合によりばらつきを改変している。)
library(ROOPSD)
library(ggridges)
library(tidyverse)
library(tidymodels)
たとえば20代後半の女性が1億人いたとしよう。
コンピュータ上で疑似的に1億人のデータを作り出した。
set.seed(202012)
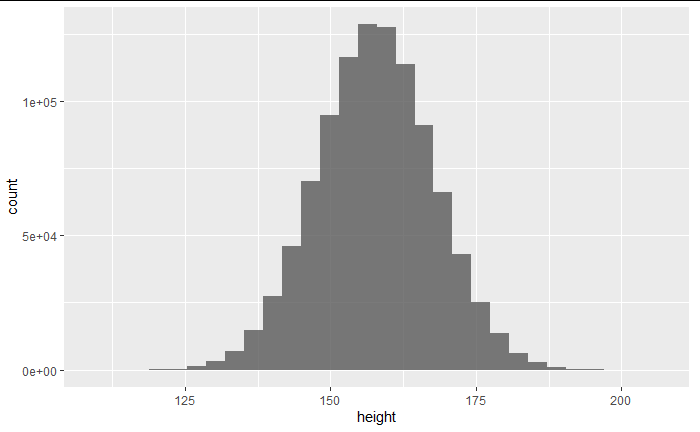
df <- data.frame(height= rnorm(1000000,157.7,10))#100まん
df <- df %>% mutate(id=c(1:nrow(df)))
g <- ggplot(df, aes(x = height)) +
geom_histogram(position = "identity", alpha = 0.8)
plot(g)
上図を20代女性の全てだと考えると、これが調査対象(母集団)であり、この平均値を求めたい。
1億人を調べることは可能か?
国の力をもってしたら可能かもしれない。
しかし、期間は何年かかるだろうか?費用は?調査人件費は?回答してくれない人は?
少数のチームごときで対応できる実験ではなさそうだ。
こんな数を集めるのはとても大変。
身近にいる友達からなんとか調べられないだろうか?
女友達10人を呼び出し、その身長の平均をもとに全国の平均を語ることができたらどれほど楽だろうか。
早速呼び出してみる。
対象の全人口が上記のデータに含まれていると考えれば、全データにIDを割り振ってやれば集めた身近な女友達にも何らかのIDが割り振られているはず。
set.seed(123)
shuffle_id <- sample(nrow(df))[1:10]
friends <- df %>% slice(shuffle_id)
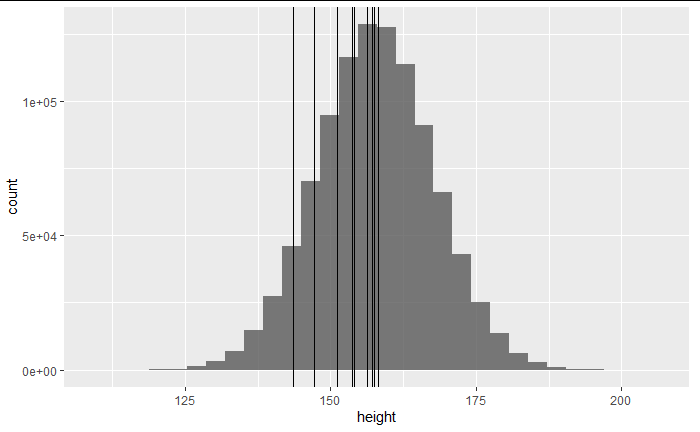
g + geom_vline(xintercept = friends$height)
10人の身長をヒストグラムの上に線で描いた。
このポイントから採取されたと解釈できる。
10人を3cm刻みでヒストグラムにする。
g2 <- ggplot(friends, aes(x = height)) +
geom_histogram(position = "identity", alpha = 0.8,binwidth = 3) +
geom_vline(xintercept = friends$height)
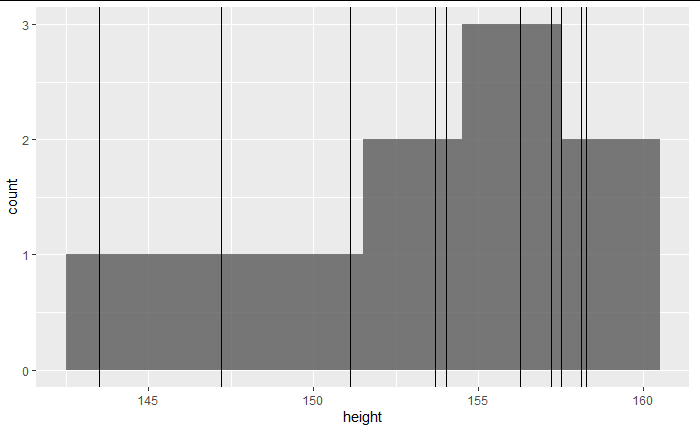
plot(g2)
採取された友人10人が一つのサンプルであり、サンプルをヒストグラムにしてみると上図のようなサンプル分布が得られる。
選ぶ友達を変えた場合はどうなるだろうか?
これを、「母集団から別のサンプルを抽出する」と考える。もしくは**平行世界では別の友達を選んだ。**とも考えられる。
結果は当然変わる。
set.seed(456)
shuffle_id <- sample(nrow(df))[1:10]
friends_2 <- df %>% slice(shuffle_id)
g + geom_vline(xintercept = friends$height) +
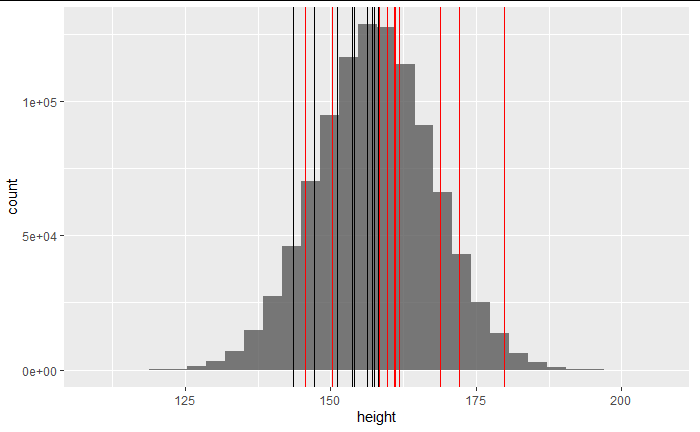
geom_vline(xintercept = friends_2$height,color="red")
2回抽出を行った。
mean(df$height)
mean(friends$height)
mean(friends_2$height)
[1] 157.7069
[1] 153.6948
[1] 161.8766
最初に呼び出した「友達グループ1」の10人の平均身長は「153 cm」。
次に呼び出した「友達グループ2」の10人の平均身長は「161 cm」。
本当の全国平均として設定したのは「157 cm」である。
たまたま選んだ友達の身長とは、これほどまでにばらつくものなので、なかなか信用ならないということが分かる。
サンプルとは、少しのことで変化してしまう不確実性の高い物であることが分かった。
採取するたびに結果が変化するようなサンプルの平均値を母集団である全国の平均値として語るのは無理がある。
では、この課題はあきらめなければならないのだろうか?
第二章『1の標本で全を知るための条件』
母集団の性質を語りたいのであれば、「母集団の性質を表しているようなサンプル」でなければいけない。
極論を言えば母集団そのもの。
次に母集団から1つだけデータが欠けたもの。
次に母集団から2つだけデータが欠けたもの。
といった具合に徐々にデータが減ることで不確実性は下がり、逆に実験的に集めやすくなる。
つまりサンプルのサイズは大きい方が不確実性が減ると言えそうである。
サンプルサイズについては後で詳細に話す。
「ヒストグラムの形状(分布)に影響を与える要素が母集団とサンプルで似ている」というのもひとつ重要な性質である。
もし、男女のデータを推定したいのであれば「サンプルの男女の割合が結果に影響を与える」という想像はつくだろう。
そのため、サンプルの男女割合と母集団の男女割合は似ていた方が信頼性は高まるだろう。
このような条件を満たしていないと、母集団の性質をサンプルから語ることが難しくなってくる。
そのために標本化(標本抽出)の手法がいくつか考えられており「標本抽出法」と呼ばれる。
無作為、層別、集落、系統などなど沢山あるが、今回は「無作為」と「層別」について少しだけ説明する。
無作為抽出
無作為は言葉の通り完全にランダムに抽出する方法。
サンプルサイズが大きければ、ランダムに選抜したとしても母集団の性質と似るものである。
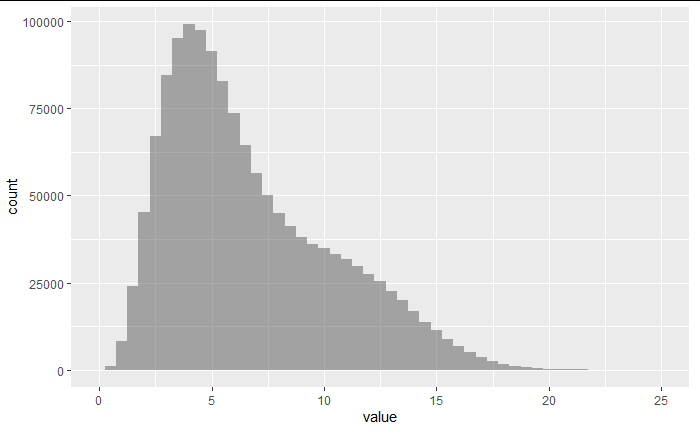
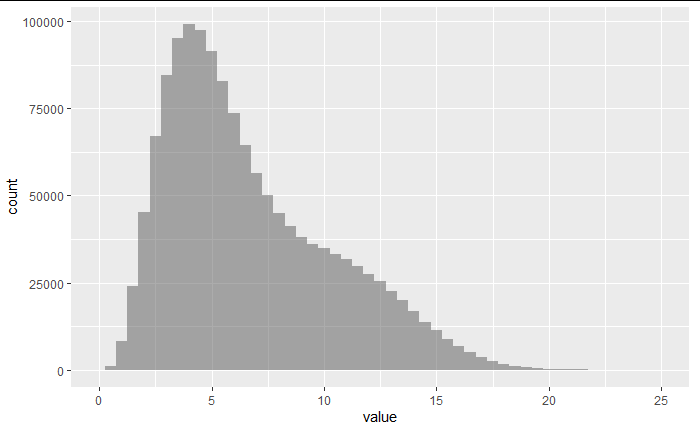
例えば、以下のような歪んだ分布からランダムにサンプリング(標本を抽出)した場合、どんな分布の形になるか確認してみよう。
set.seed(123)
n=1000000
da<-rgamma(n,5,rate = 1)
nois<-rnorm(400000,11,3)
pop<-as.tibble(c(da,nois))
pop$value<-abs(pop$value)
pop %>% ggplot(aes(x = value))+
geom_histogram(binwidth=0.5,alpha = 0.5)+
xlim(0,25)
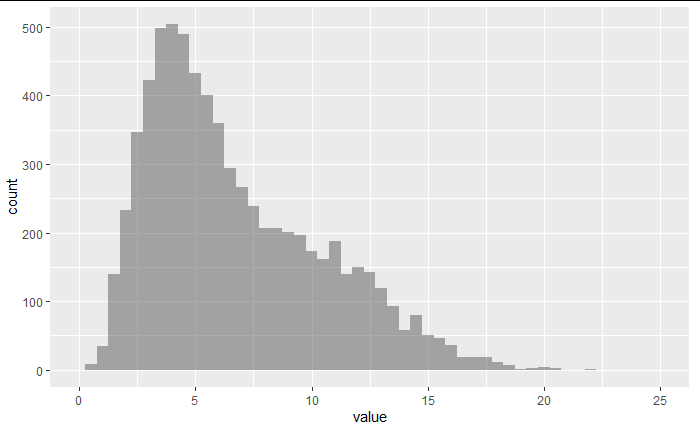
上図のような歪んだ分布から、無作為に大きなサンプルを抽出した結果が下図。
sample_data <- initial_split(data=pop,prop = 0.995)
test<-testing(sample_data)
test %>% ggplot(aes(x = value))+
geom_histogram(binwidth=0.5,alpha = 0.5)+
xlim(0,25)
形を保持して抽出できている。
ただし、あくまでもサンプルサイズが大きい時の場合であり、データが少ない時にはいくらか工夫が必要になる。
分布を四分位に分割しそれぞれの範囲で抽出を行う場合や、分布に影響を与える要素に注目しながら割合を保持するような抽出を行うなど。
層別抽出
もうひとつは層別抽出。
男女という要素は母集団の平均身長に影響を及ぼすだろうし、年齢もまた影響があるだろう。
推定したい母集団の人口では、年齢や性別という要素の割合がサンプルでも等しくなるようにしようという抽出方法。
これを特に比例配分法という。
サンプルセレクションバイアス
サンプルの抽出時に気を付けるべき点としてこれも紹介しておく。
もしも、友達がバレー部やバスケットボール部であった場合、友達の身長は高い人ばかりになるだろう。
このように、サンプルの選び方次第で母集団の性質を全く表せないサンプルが得られてしまい、母集団の性質を議論するためには、まったく役に立たない標本となってしまう。
身長の例ならばまだいい。
薬の副作用が無いかを試す試験などで治験対象に偏りがあった場合、正確な薬の評価ができたとは言いにくくなる。
より詳しく知りたければ、ランダム化比較試験(RCT:randomized controlled trial)、もしくは無作為化比較試験で調べてみてもらいたい。
細かい抽出方法を紹介したところで、
「サンプルのサイズ」と「特別ば分布の場合」についても紹介していく
第三章『信頼のおける標本』
3-1:サンプルのサイズと信頼性
サンプルサイズが大きければ母集団の性質が似る。
1回で何人の友達を呼べば信頼できる結果が得られるだろうか。
今までの例では10人の友達を標本としたが、もし20人集めた標本をつくり標本平均である平均身長を計算した時、母平均の関係はどうなっているだろうか?
50人では?
100人では?
200人では?
シミュレーションしてみよう。
set.seed(789)
shuffle_id <- sample(nrow(df))[1:200]
friends_20 <- df %>% slice(shuffle_id[1:20])
friends_50 <- df %>% slice(shuffle_id[1:50])
friends_100 <- df %>% slice(shuffle_id[1:100])
friends_200 <- df %>% slice(shuffle_id)
paste("population mean",round(mean(df$height),2))
paste("20 friends",round(mean(friends_20$height),2))
paste("50 friends",round(mean(friends_50$height),2))
paste("100 friends",round(mean(friends_100$height),2))
paste("200 friends",round(mean(friends_200$height),2))
[1] "population mean 157.71"
[1] "20 friends 156.13"
[1] "50 friends 157.03"
[1] "100 friends 157.66"
[1] "200 friends 158.51"
先ほどの10人では153や161といった標本平均であったが、50人を集めた段階から真の平均である母平均の値157に近い平均値となってきている。
3-2:サンプルのサイズとばらつき
少数人ではたまたま身長が高い人だけ集まってしまう場合もあるだろうから、20人や50人の時は、平均値のバラツキが大きくなるだろう。
しかし、一点の値だけでばらつきをイメージすることは難しい。
今回、20人の時に出た平均値がたまたまおかしなサンプルを取ってきたために出た値かもしれない。
逆に、200人集めたとしても、十分に母集団の平均値に近いと見なせないのであれば、200人も集めるコストをかけたのがムダになってしまう。
せっかくコンピュータ上でシミュレーションできるのだから確認してみよう。
set.seed(789)
df2 <- df %>% mutate(group_20 = rep(1:(nrow(df)/20), length = nrow(df)),
group_50 = rep(1:(nrow(df)/50), length = nrow(df)),
group_100 = rep(1:(nrow(df)/100), length = nrow(df)),
group_200 = rep(1:(nrow(df)/200), length = nrow(df)))
df2 %>% group_by(group_20) %>%
summarise(sample_mean = mean(height)) %>%
slice(1:5000) %>%
ggplot(aes(x = sample_mean)) +
geom_histogram(position = "identity", alpha = 0.8,binwidth = 1) +
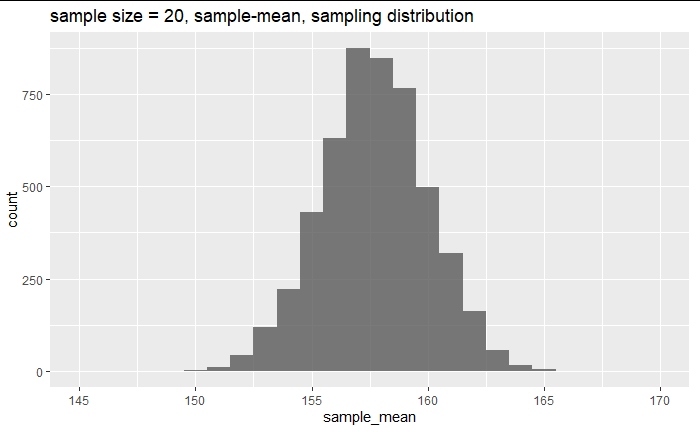
labs(title="sample size = 20, sample-mean, sampling distribution") +
xlim(145,170)
20人のサンプリング分布は上図のような広がりを持っている。
df2 %>% group_by(group_50) %>%
summarise(sample_mean = mean(height)) %>%
slice(1:5000) %>%
ggplot(aes(x = sample_mean)) +
geom_histogram(position = "identity", alpha = 0.8,binwidth = 1) +
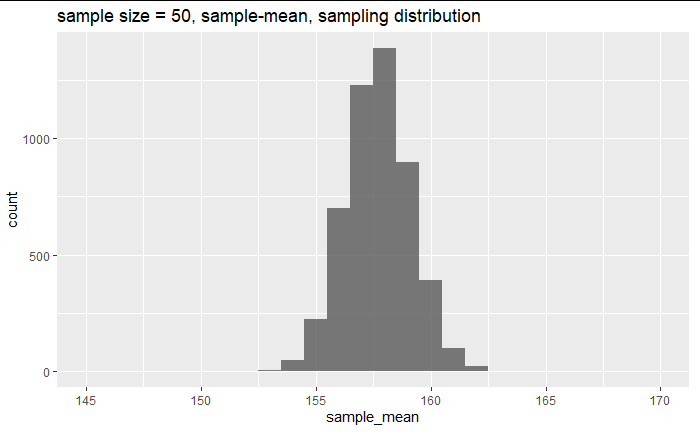
labs(title="sample size = 50, sample-mean, sampling distribution") +
xlim(145,170)
50人のサンプリング分布。
df2 %>% group_by(group_100) %>%
summarise(sample_mean = mean(height)) %>%
slice(1:5000) %>%
ggplot(aes(x = sample_mean)) +
geom_histogram(position = "identity", alpha = 0.8,binwidth = 1) +
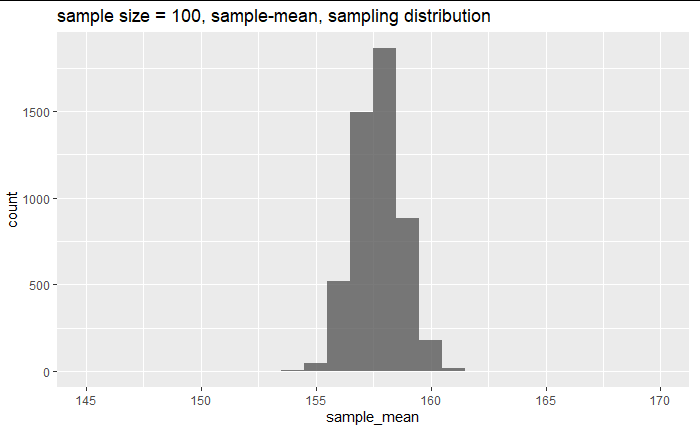
labs(title="sample size = 100, sample-mean, sampling distribution") +
xlim(145,170)
100人のサンプリング分布。
df2 %>% group_by(group_200) %>%
summarise(sample_mean = mean(height)) %>%
slice(1:5000) %>%
ggplot(aes(x = sample_mean)) +
geom_histogram(position = "identity", alpha = 0.8,binwidth = 1) +
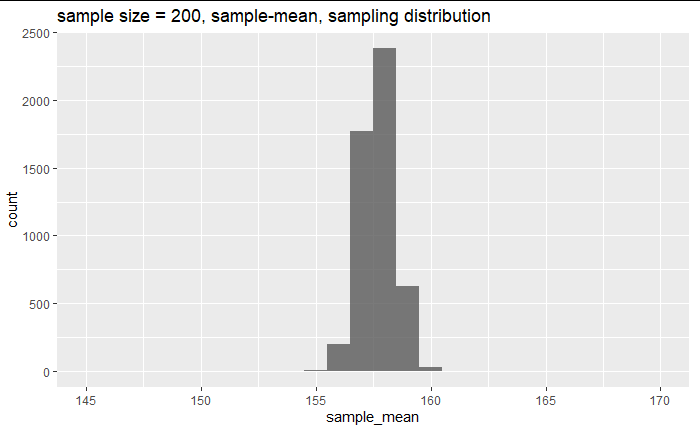
labs(title="sample size = 200, sample-mean, sampling distribution") +
xlim(145,170)
200人のサンプリング分布。
「サンプルサイズの違いによる標本平均のばらつき」を確認するヒストグラムを作った。
じつはこれが対数の法則と関係を持っているわけで、「膨大な回数の試行結果の値は真のパラメタに収束する(サンプルサイズの大きい標本平均は母平均に収束する)」ということに繋がります。
サンプリング分布(統計量のばらつきを表現できる分布)が一点に収束していくので、さらに200,300と増やしていけばばらつきが小さくなるのが想像できる。
サンプルサイズと標本統計量のばらつきに関係があることが分かってもらえると思う。
- くどいが、分かったことを復習。
- サンプルのサイズを大きくすると?
- 標本統計量である標本平均は、母平均を中心とした分布になり、そのばらつきは小さくなる
- つまり、「サンプルサイズが大きければ、標本平均が母平均に近いと自信を持って言える」ことが分かる
- ばらつきが小さいということは、たまたま偶然大外れのサンプルだったとしても、統計量が母平均に近くなるから
- 逆にサンプルサイズが小さければ?
- 「たまたま偶然大外れのサンプル」を取ってきたとすると、母平均から大きく外れた標本平均の値となる
- これを母平均の推定値である、というには少々不安が残ってしまう
- サンプルのサイズを大きくすると?
しかし、現実では日程やコストの都合で「サンプリング分布」をつくるほどの実験はできない。
シミュレーションができない場合はどのようにサンプルサイズを決めたらいいのだろうか?
母集団の分散がわかっている場合には分布を「えいや」と決めてしまい、中心極限定理により決めてしまう方法がある。
これに対しては後にもすこしだけ紹介するが、専門の本が出ているのでそちらを参考にして欲しい。
そして、この問題をシミュレーションできるようにしたのが本題のリサンプリング法である。
リサンプリング法は後章まで待っていただきたい。
3-3:特別な分布とサンプルサイズの関係
先に言ってしまうが、ここで話したいのは中心極限定理の話。
これは、標本が正規分布だろうが、二項分布だろうが、歪んだ分布だろうが、サンプル数を増やしてヒストグラムを描くとサイズnから成るサンプルの場合、
nが大きいとき、確率変数(標本平均)\bar{X}は平均値\mu、分散\frac{\sigma^2}{n}の正規分布に従う。
という性質。
確率分布について馴染みが無い場合には以前勉強会で使った資料を紹介しておく。
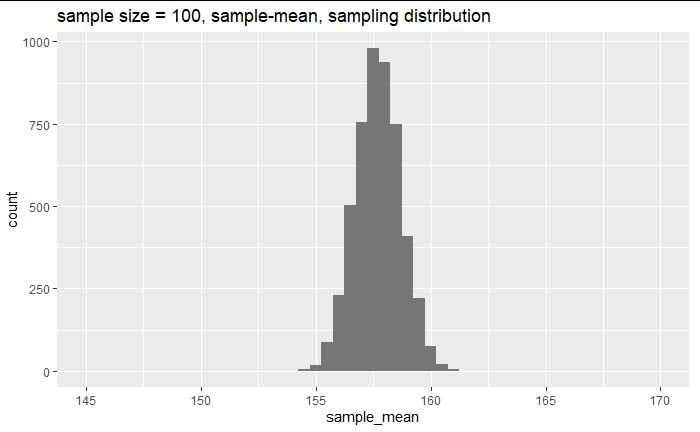
たとえば母集団が正規分布ならば、サンプリングした結果のサンプリング分布は下図のようになる。
df2 %>% group_by(group_100) %>%
summarise(sample_mean = mean(height)) %>%
slice(1:5000) %>%
ggplot(aes(x = sample_mean)) +
geom_histogram(position = "identity", alpha = 0.8,binwidth = 0.5) +
labs(title="sample size = 100, sample-mean, sampling distribution") +
xlim(145,170)
このサンプリング分布の平均やばらつきを確認してみると、
res<- df2 %>% group_by(group_100) %>%
summarise(sample_mean = mean(height)) %>%
slice(1:5000)
paste("n=100 sample mean =",round(mean(res$sample_mean),3))
paste("n=100 sample sd =",round(sd(res$sample_mean),3))
paste("population mean =",round(mean(df$height),3))
paste("population sd =",round((sd(df$height)/sqrt(100)),3))
[1] "n=100 sample mean = 157.715"
[1] "n=100 sample sd = 0.995"
[1] "population mean = 157.707"
[1] "population sd = 0.999"
確かに理論通りになっている。
歪んだ分布からのサンプリング分布では、
pop_2 <- pop %>% mutate(group_100 = rep(1:(nrow(pop)/100), length = nrow(pop)))
pop_2 %>% group_by(group_100) %>%
summarise(sample_mean = mean(value)) %>%
slice(1:5000) %>%
ggplot(aes(x = sample_mean)) +
geom_histogram(position = "identity", alpha = 0.8,binwidth = 0.1) +
labs(title="")
res <- pop_2 %>% group_by(group_100) %>%
summarise(sample_mean = mean(value)) %>%
slice(1:5000)
サンプリング分布が正規分布になっている。
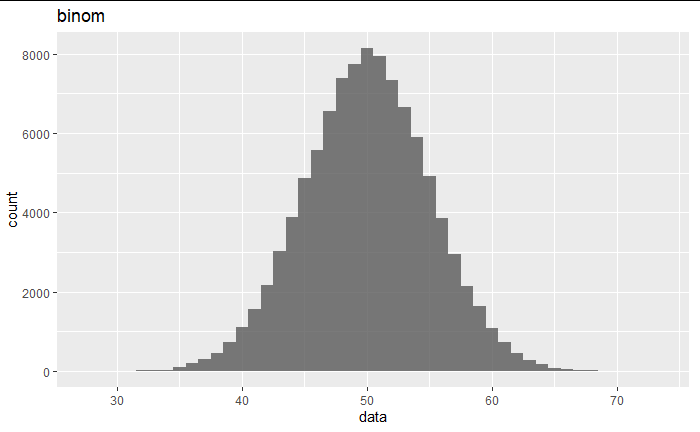
コインに見られるような二項分布でも、
set.seed(123)
binom_data <- data.frame(data=rbinom(100000,100,0.5))
binom_data %>%
ggplot(aes(x=data)) +
geom_histogram(position = "identity", alpha = 0.8,binwidth = 1) +
labs(title="binom")
正規分布になっている。
余談:分散がσ^2/nになっていない、と思った人は、「母集団が二項分布の場合の標本平均の極限分布」で調べてみて欲しい。
二項分布の正規分布への近似は中心極限定理の中の少し変化球なパターンである。
簡単に記入しておくと、分散の期待値V[X]はnp(1-p)であるが、
二項分布は標準正規分布
(x_bar - p) / {sqrt(p(1-p))/sqrt(n)}
に変換できる。
以上のように、「統計量(サンプリング分布)が正規分布になる」という性質を利用して、統計量の推定や検定、差の検定などを行うのが推測統計であり、統計検定2級はここがメインとなる。
第四章『再標本化(リサンプリング)と統計的学習』
標本化を行う際に注意すべき視点と、統計量のサンプリング分布の関係を紹介してきた。
サンプリングについてザックリと紹介できたと思う。
ここから「サンプリングされた標本(サンプル)」から「再度サンプリングを行う再標本化(リサンプリング)」を行います。
何のために行うのか、どんな嬉しいことがあるのか、確認していきましょう。
4-1:リサンプリングの活用方法
サンプリングは母集団から、「母集団の性質を保持した標本データを入手して、母集団の性質について議論する」という目的がありました。
リサンプリングは推測・予測のどちらの面でも活用方法があります。
例えば推測統計の場合はブートストラップ法を使い、統計量について手元の一つのデータでは知ることが出来ない部分である信頼区間をデータ駆動で求め議論できるようにする。
予測モデルを作っている人では、「訓練、テスト、検証」のデータセットを作る事がリサンプリング。
予測モデルの作成時にもブートストラップ法が使われるようになっています。
はじめに簡単に予測モデルの例を紹介し、その後推測統計でのブートストラップ法を紹介していきます
4-2:予測モデルのリサンプリング「train,test,valid」
いわゆるtest,train,validのデータセットです。
予測モデルとは、「未知のデータを予測したい」という気持ちがあります。
(クロスバリデーションの細かい種類の説明は飛ばします)
万人に伝わりやすい予測モデルの例として株価を考えてみます。
今までの過去のデータは手元にあり、未来の株価が分かれば資産を増やすことが出来るかもしれません。
しかし、過去のデータの範囲だけはカンペキに予測することが出来ても、未来を予測することが出来なければ意味がありません。
「過去のデータ」を分割し、一部のデータを隠してモデルを作り、作ったモデルで隠したデータを正確に予測できるかを確認します。
そのためにも、手元のデータを「等しい性質を持った、訓練用と確認用の小集団」に分割する必要があります。
この時にリサンプリングを使うわけです。
(株価のような時系列サンプリングは、より複雑な考え方が必要なため今回は紹介しません。)
split_data <- df %>% initial_split(prop=0.7)
split_data
<Analysis/Assess/Total>
<700000/300000/1000000>
R言語のinitial_splitのstrataオプションで層別サンプリングを行うことを指示出来るので、男女のような数値に影響を与える要素がある場合には性質を保持した小集団にするためにも指定してあげましょう。
rsampleではtest,trainという名前は他のデータ名と被る可能性があるため、Analysis(訓練,train)/Assess(確認,test)という名前になるように設計されています。
予測モデルをtrainで作り、testデータを使って評価を行うわけですが、もしその評価結果が悪かった場合は再度パラメタを変更してtrainで訓練を行います。
すると最終的にはtestに対して良い成果を出せるモデルが出来るようになります。
しかし、予測モデルの達成したかった目的は、「未知のデータを予測する」事でした。
勉強の筆記試験もそうですが、カンニングして再度学習したらその問題は解けるようになって当然です。
「未知のデータに使える」という評価にはならないでしょう。
(数学をチャート式で勉強した後、何度も同じ模擬試験を受けて、再度チャートを勉強して、同じ模擬試験を受けて、、、と繰り返しても未知の試験内容に変わった時に対応できるとは思えません)
そこで、さらにもう一つデータを分割しておきます。
これを「validation(検証)」と呼びましょう。
validationを模擬試験とし、testは本番試験です。
testを受けていいのは1回だけで、testの結果を受けてモデルの再訓練は絶対に行いません。
一切カンニングしていない「test」での精度は「未知のデータに対する精度」として評価できるようになります。
4-3:データの量と分割
精度検証を行うためのデータ分割手法は、再度データを取れない場合(コストが高い、コンペの公開データのみ等)
の策の一つなので、いくらでも新しいデータを採取できる場合には、(新しいデータの性質がシフトしていない場合)分割という考えも不要だったりします。
特にデータの量が大きければ、網羅的なパターンを訓練データが持っていると考えられる場合もあります。
絶対に予測モデルを作るときにはリサンプリングをしなければならないわけではありません。
データが大変に少量しか無い場合にはtestには極力データを割かずに殆どを訓練に使うことも可能です。
タスクによっては精度評価は必要なく、モデルをリリースした後に徐々に調節していくことが可能な場合などは手元のデータすべてを訓練に回すこともあります。
別のアプローチとして交差検証やブートストラップ法によってサンプルを「疑似的に増やす」方法もあります。
4-4:予測モデルのリサンプリング「v-fold(k-fold) cross validation」
train,test,validの分割だけで良いのでしょうか?
サンプリングの時にもお話しましたが、サンプルは選び方でばらつきます。
小集団の平均値はサンプルサイズが大きい時にはある程度収束しますが、それでもばらつきを持っています。
ばらついた分割データかもしれないデータで訓練したモデルを信じていいのでしょうか?
test結果を信じてもいいのでしょうか?
ならば分割方法も様々なパターン試そう!
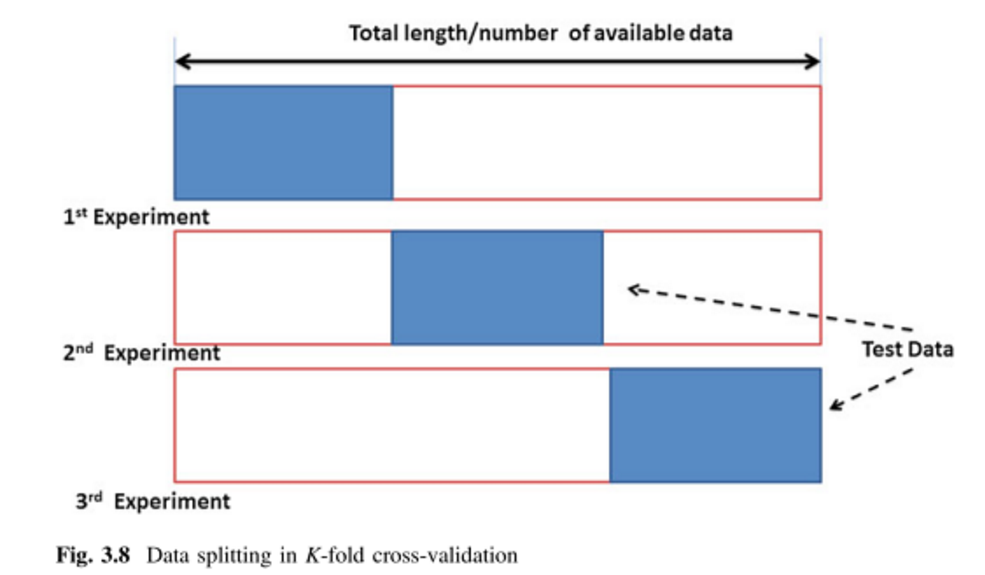
ということでv-foldの考え方が出てきます。
v-foldはtrain,testに分割した後、trainをv個に分割し、一つをvalidに設定し残ったv-1個で訓練を行います。
訓練データとvalidの設定方法はv通りあるので、v個のモデルが出来上がります。
すると、あるパラメータで訓練した予測モデルの「平均的な精度」が計算できるようになるというメリットまであります。
こうしてサンプリングによるばらつきを減らしながら、選択したモデル(アルゴリズム,パラメータ)がデータに対して精度を得られるか、も評価できるようになるわけです。
vを増やしすぎると性質の保持が難しくなり、v-foldの恩恵が薄まるので5~10が選択されます。
Hydrological Data Driven Modelling: A Case Study Approach
K-fold vs. Monte Carlo cross-validation
4-4:予測モデルのリサンプリング「Nested Cross Validation」
v-foldを紹介しましたが、このままではまだ過学習の可能性があります。
testが固定されてしまっているためです。
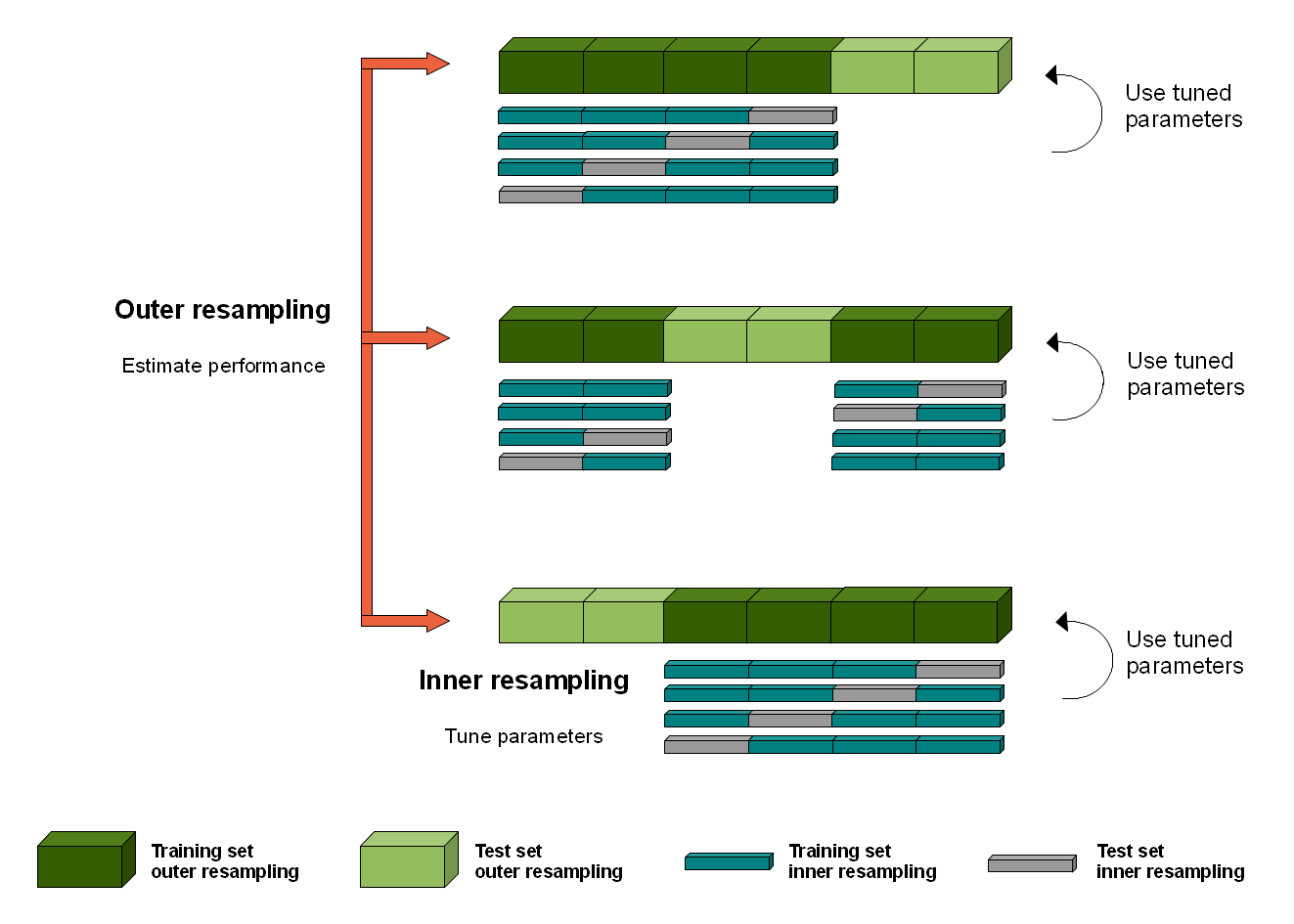
ここで、リサンプリングによる分割を二段階に行うことを考えます。
一段階目はtestとtrainを切り分けるためのv-foldを行う。
二段階目はtrainからvalidationを切り分けるためのv-foldを行う。
すると、testという小集団のばらつきが軽減され、「たまたま偶然良い精度が出た」という誤った結果を抑制することができます。
Nested Cross Validation for Algorithm Selection
What's the meaning of nested resampling
第五章『推測統計のリサンプリング』
ここでは主にブートストラップ法に焦点を当てて紹介したい。
予測モデルにもブートストラップ法によって得た小集団をクロスバリデーションの一種として使う手法があるが、それは各自で調べて頂きたい。
5-1:ブートストラップ法とは
ブートストラップ法とは、簡単に説明すると標本データから重複を許すような復元抽出を行う事で「疑似標本」を作り出すことである。
R言語であれば、sample()関数のreplaceをTRUEにするとイメージが掴めるかと。
このようにしてブートストラップ法によってリサンプリングすることをブートストラップ標本抽出と呼び、作り出したサンプルを「ブートストラップ標本」と呼ぶ。
この場合は単に復元抽出であり、特にノンパラメトリックブートストラップ標本と呼ぶ。
(パラメトリックではリサンプリング時に疑似的な新しいサンプルになるよう問題のないノイズを加えるなどを行う。)
身長を例にした標本化の話では、母集団全体を作り出しそこから複数回標本をサンプリングしてきた。
機械的なサンプリングなので複数回行うことが出来たが、実際には
・50人や100人の女性をランダムに選び
・協力してもらい
・データ利用の許可をもらい
・場所を確保し
・人員を手配し
・身長を測定する
など実現させることは大変である。
そのため標本データは一つしかない場合が多い。
では一つの標本集団の平均値からどのように母集団について議論するのか?
方法は中心極限定理を使って、母集団の平均値や分散を推定する方法がある。
この場合、母集団や標本が特定の分布に従っているという前提が必要であるため、事前に性質が分かっている対象には有効である。
しかし、母集団の分布や標本の分布などの情報が分からなかった場合は?
そこで出てきたのが、一つの標本から情報を取り出すためのブートストラップ法というリサンプリング手法である。
5-2:標本とブートストラップ標本の分布
先ほど作成した歪んだ分布を使ってブートストラップサンプルを作り出してみよう。
pop %>% ggplot(aes(x = value))+
geom_histogram(binwidth=0.5,alpha = 0.5)+
xlim(0,25)
上図のような母集団から、
set.seed(595)
sample_data <- initial_split(data=pop,prop = 0.999985)
test<-testing(sample_data)
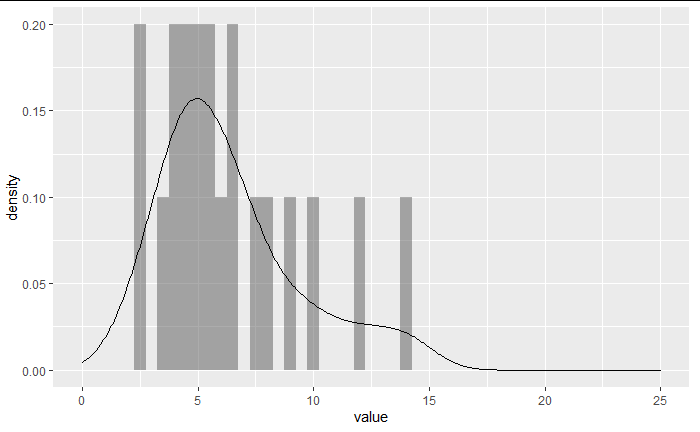
test%>%ggplot(aes(x = value))+
geom_histogram(aes(y=..density..),binwidth=0.5,alpha = 0.5)+
geom_density()+
xlim(0,25)
標本を取り出す。
今は唯一この1つの標本しか手に入っておらず、それでも母集団の平均値を求めたいという課題があるとする。
しかし、サンプリング分布が求められるのであれば、母集団を平均とした正規分布が表現できるのだが、これができない。
そこでブートストラップ標本による疑似的なサンプリング分布「ブートストラップ-サンプリング分布」を作ろうと思う。
このブートストラップ標本はもしサンプリングをもう一度行ったならば、こんな結果になるだろうなという標本と考えられる。
平行世界で標本を抽出した結果と考えてもいいかもしれない。
set.seed(700)
bootstrap_sample <- bootstraps(test, times = 1000)
f2 <- function(x){d<-as.data.frame(x)}
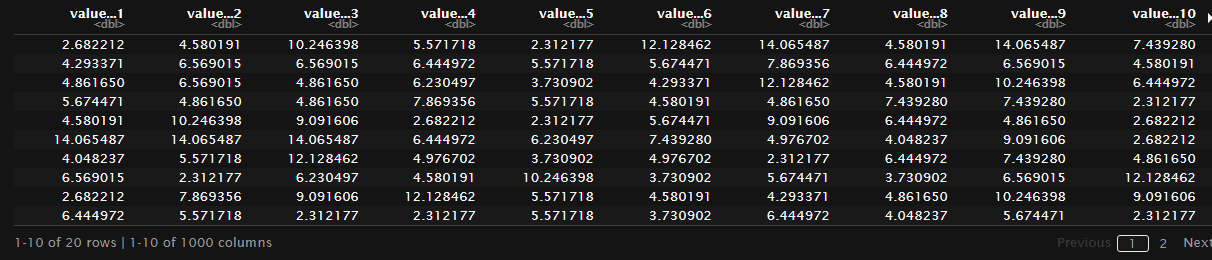
map_dfc(bootstrap_sample$splits,f2)
復元抽出によってブートストラップ標本を1000個作成した。
bootstrap_all_data <- map_df(bootstrap_sample$splits,f2)
bootstrap_all_data %>% ggplot(aes(x = value))+
geom_histogram(aes(y=..density..),binwidth=0.5,alpha = 0.5)+
geom_density()+
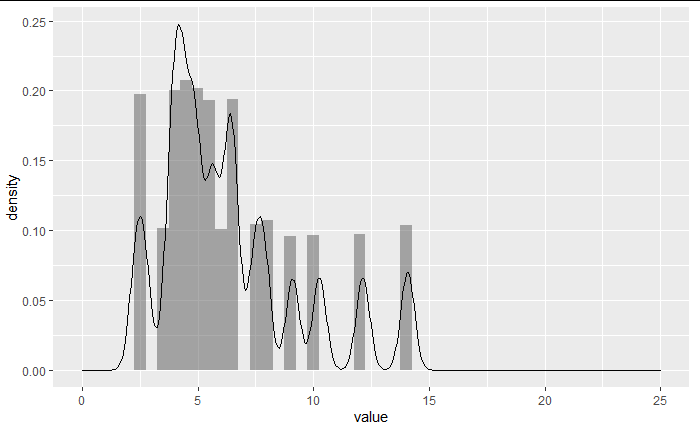
xlim(0,25)
ブートストラップ標本全体をヒストグラムにすると、もとの標本分布に似た形になっていることが分かる。
ブートストラップ標本は、標本からランダムに復元抽出されるため、各ブートストラップ標本にはばらつきが生まれるが、全体を通してみると標本と似た分布になる。
f <- function(x){
d<-as.data.frame(x)
mean(d$value)}
boot_resample_mean <- data.frame(val = map_dbl(bootstrap_sample$splits,f))
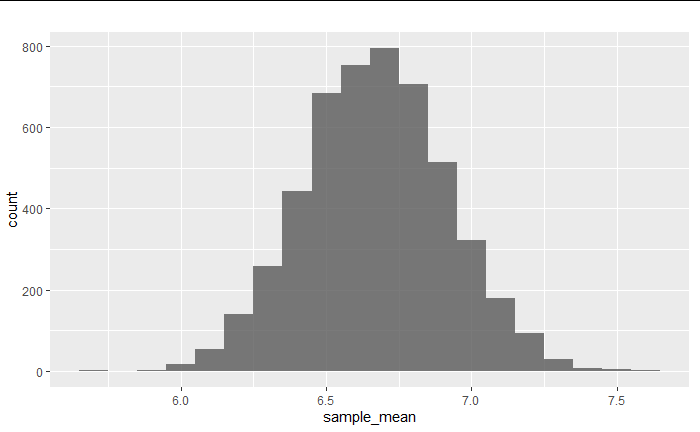
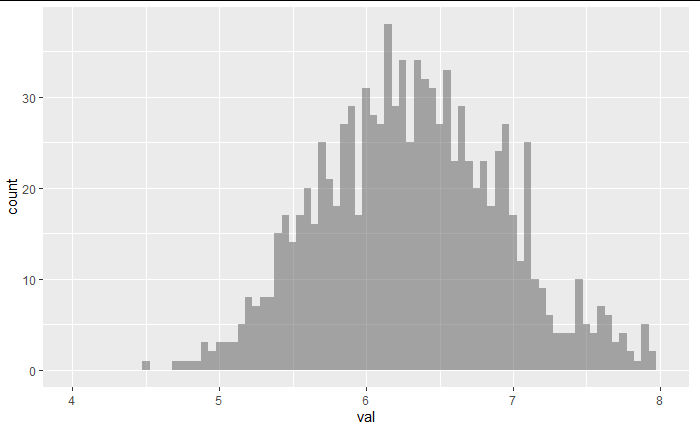
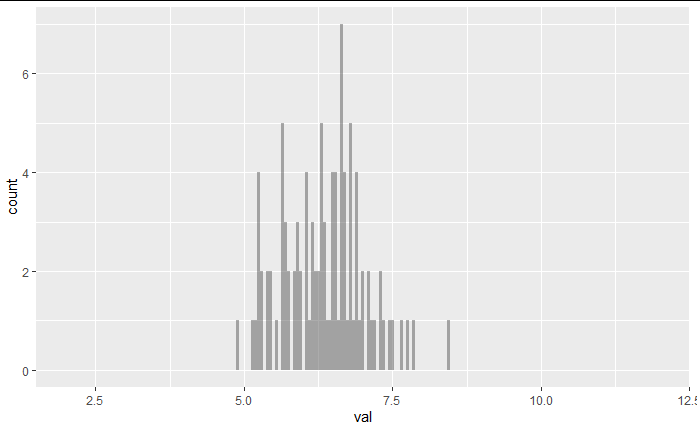
boot_resample_mean %>% ggplot(aes(x = val))+
geom_histogram(binwidth=0.05,alpha = 0.5)+
xlim(4,8)
ブートストラップ標本たちによって得られた平均値の分布「ブートストラップ-サンプリング分布」。
標本の分布が歪んでいるので重複を許したブートストラップ-サンプリング分布も歪む。
標本平均という標本から一つしか得られないはずの統計量がブートストラップ標本によって分布として表現された。
こうすることで、標本平均の持つバイアス、バリアンスや、予測モデルでは予測誤差などが表現できるようになる。
その平均値はもとの標本の平均値へと収束する。
mean(test$value)
mean(boot_resample_mean$val)
[1] 6.345229
[1] 6.342678
真の平均には収束しない。
5-3:ブートストラップ-サンプリング分布のばらつき
母集団から複数回サンプリングできた場合のサンプリング分布のばらつき
と
ブートストラップ-サンプリング分布のばらつき
は近い値になるという性質がある。
そのため、本来得られないはずの「サンプリング分布のばらつき(標準誤差)」の推定値(代理)として、ブートストラップ-サンプリング分布の標準誤差が採用される。
pop_3 <- pop %>% mutate(group_20 = rep(1:(nrow(pop)/20), length = nrow(pop)))
res <- pop_3 %>% group_by(group_20) %>%
summarise(sample_mean = mean(value)) %>%
slice(1:1000)
sd(res$sample_mean)
sd(boot_resample_mean$val)
[1] 0.5425073
[1] 0.6548191
5-4:ブートストラップ標本を増やす
set.seed(800)
bootstrap_sample <- bootstraps(test, times = 100)
f <- function(x){
d<-as.data.frame(x)
mean(d$value)}
boot_resample_mean <- data.frame(val = map_dbl(bootstrap_sample$splits,f))
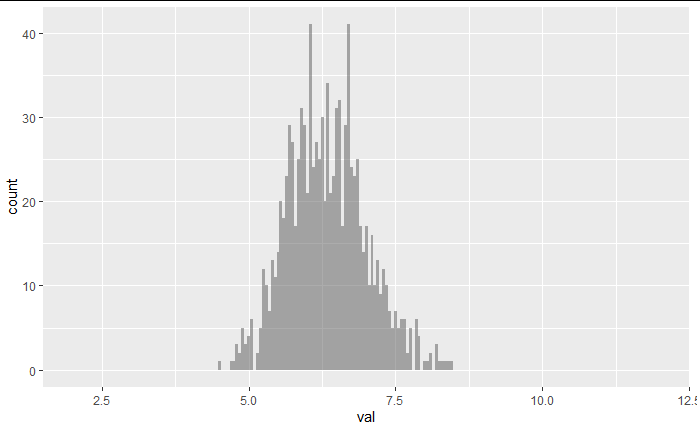
boot_resample_mean %>% ggplot(aes(x = val))+
geom_histogram(binwidth=0.05,alpha = 0.5)+
xlim(2,12)
set.seed(800)
bootstrap_sample <- bootstraps(test, times = 1000)
f <- function(x){
d<-as.data.frame(x)
mean(d$value)}
boot_resample_mean <- data.frame(val = map_dbl(bootstrap_sample$splits,f))
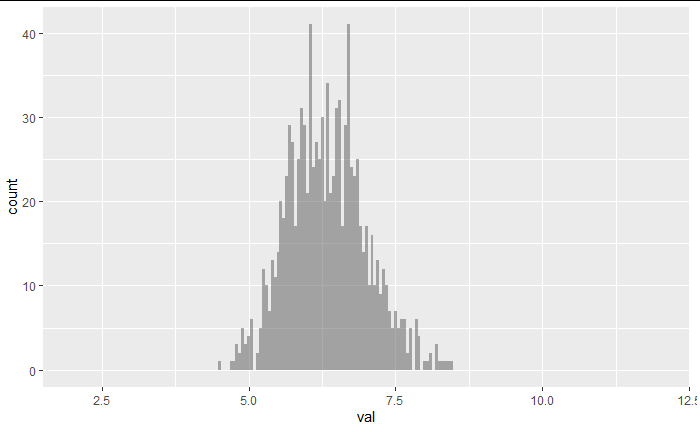
boot_resample_mean %>% ggplot(aes(x = val))+
geom_histogram(binwidth=0.05,alpha = 0.5)+
xlim(2,12)
set.seed(800)
bootstrap_sample <- bootstraps(test, times = 1000)
f <- function(x){
d<-as.data.frame(x)
mean(d$value)}
boot_resample_mean <- data.frame(val = map_dbl(bootstrap_sample$splits,f))
boot_resample_mean %>% ggplot(aes(x = val))+
geom_histogram(binwidth=0.05,alpha = 0.5)+
xlim(2,12)
set.seed(800)
bootstrap_sample <- bootstraps(test, times = 100000)
f <- function(x){
d<-as.data.frame(x)
mean(d$value)}
boot_resample_mean <- data.frame(val = map_dbl(bootstrap_sample$splits,f))
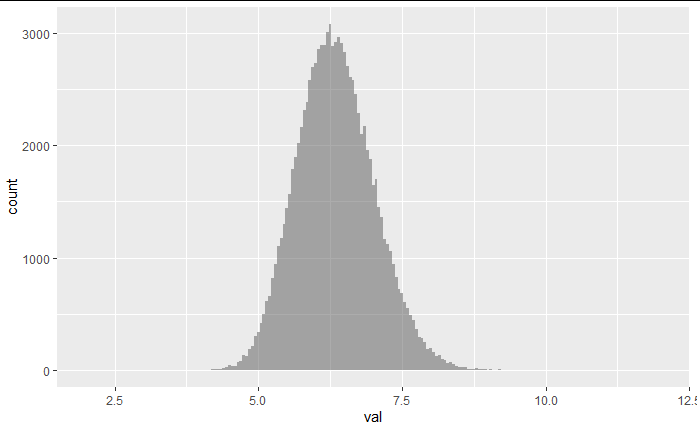
p <- boot_resample_mean %>% ggplot(aes(x = val))+
geom_histogram(binwidth=0.05,alpha = 0.5)
p+xlim(2,12)
段々となめらかなベル型になっていく。
これは、標本を母集団としたときのサンプリング分布のようなものになっている。
この手元のサンプルが母集団を表現しているならば、標本平均の近くに母平均があるはず(中心極限定理)。
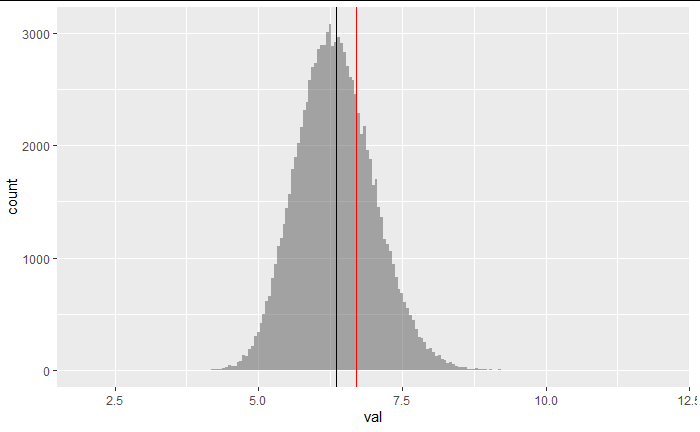
上のベル型になったブートストラップ-サンプリング分布に赤で上書きしてみる。
p+ geom_vline(xintercept = mean(pop$value),col="red") + geom_vline(xintercept = mean(boot_resample_mean$val))+xlim(2,12)
統計2級で登場する「平均や比率の差の検定」では、理論的なリサンプリング分布の信頼区間に0が入っているかどうかを考えるが、ブートストラップ法では理論的でないデータ駆動のブートストラップ-サンプリング分布をサンプリング分布として扱うことで、より視覚的・直観的に理解が出来るようになる。
ブートストラップ法ではブートストラップ-サンプリング分散の分散が、サンプリング分布の分散σ2/nの良い近似になるのでこれを使用する。
5-5:一旦古典統計の母平均の推定
標本平均とは、母平均を中心にσ2/nの範囲に収束する。
逆に、標本平均からσ2/nの範囲を監視してやれば、「母平均も入っているはず」。
しかし母集団が分からないのだから、母分散が分からないという問題も残っている(統計2級の筆記試験では母分散が与えられている場合が多い)。
これが古典統計の良くある母平均推定の話。
mu <- 100
sigma <- 10
n <- 50
ci_low <- mu - 1.96 * sqrt(sigma) / sqrt(n)
ci_high <- mu + 1.96 * sqrt(sigma) / sqrt(n)
for(o in 1:20){
count <- 0
for(i in 1:100){
my_sample <- rnorm(n = n, mean = mu, sd = sqrt(sigma))
sample_mean <- mean(my_sample)
sample_sd <- sd(my_sample)
if((sample_mean > ci_low & ci_high>sample_mean) == TRUE){count <- count + 1 }
}
print(paste0(o,"th include TRUE mean in CI : count =",count))
}
20回くらい試してみたが、だいたい標本平均から95%信頼区間の範囲に100回中95回くらいが入っている。
これが正規分布を仮定した場合の考えである。
5-6:ブートストラップ法での母平均の推定「パーセンタイル法」
サンプリング分布のバラツキが理論的に「σ2/nのバラツキをもった正規分布に収束する」という仮定のもとで95%信頼区間を考えると母平均がその範囲に入っていたはずである。
ここではブートストラップ法によるブートストラップ-サンプリング分布の95%区間を使用することで、サンプル自体の歪みや母集団の歪みを考慮する。
1000のブートストラップ標本を作ったのならば、ブートストラップ標本平均の値の大きい側と小さい側から2.5%ずつを除いた範囲が95%信頼区間となる。
これをパーセンタイル信頼区間と呼ぶ。
boot_resample_mean <- boot_resample_mean %>% rename(stat=val)
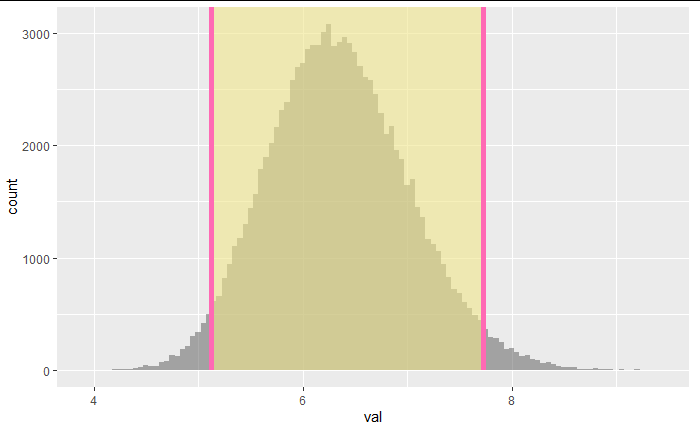
percentile_ci <- boot_resample_mean %>% get_confidence_interval(level = 0.95, type = "percentile")
p+shade_ci(endpoints = percentile_ci, color = "hotpink", fill = "khaki")
パーセンタイル法をより改善した方法にBCa法(baias-correction)がある。
5-7:ブートストラップ法での母平均の推定「標準誤差法」
ブートストラップ-サンプリング分布を正規分布だと仮定して、歪みを考えず標準誤差の95%範囲を考える。
データを元にした範囲でなく、古典統計の母平均の推定と同じ考えで範囲を考えるもの。
この方法を使う場合には事前に分布が正規性を持っているかQQplotなどで確認するのが望ましい。
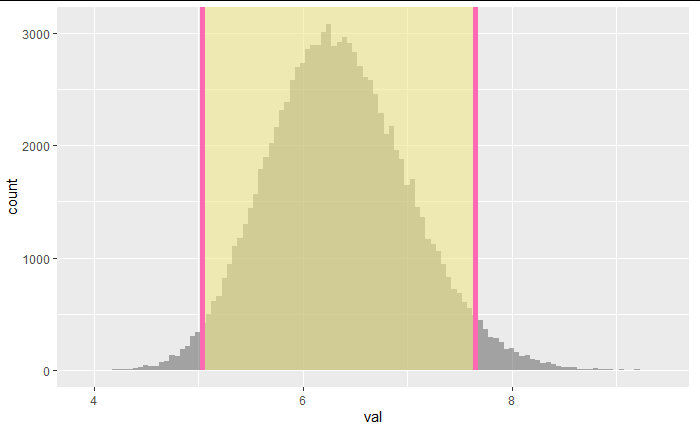
standard_error_ci <- boot_resample_mean %>%
get_confidence_interval(type = "se", point_estimate = mean(test$value))
p+shade_ci(endpoints = standard_error_ci, color = "hotpink", fill = "khaki")
他にもいくつかの信頼区間を求める方法がある。
より母平均などのパラメタを精度良く捉えられる方法が望ましいが、パーセンタイル法、標準誤差法、のどちらが精度の良い信頼区間というワケではない。
当然うまく機能しない場合もあるが、一般的にこの二つが代表として使われる。
適した方法を紹介、なんてことはできないが疑似的なサンプリング分布が得られた。
統計量やパラメタのバラツキを知ることができる方法であるので、不確実性の可視化などには役立てると思う。
エピローグ『信頼区間に真の平均値が含まれているか確認』
最後にブートストラップ法でも古典統計の例と同じように信頼区間の中に母平均が存在するか確かめてみる。
母集団からサンプルをn個取り出す。
サンプルから復元抽出してブートストラップ標本をQ個作る。
Q個それぞれで標本平均を作る
ブートストラップサンプリング分布を作る
パーセンタイル区間を求める。比較のため標準誤差法も使う。
母集団の真の平均が含まれているかチェックする。
これを100回繰り返した時、母集団の真の平均がいくつ入っているのか。
どの信頼区間が母平均を当てられるのかを調べるためのスクリプトを紹介して終わりにする。
set.seed(500)
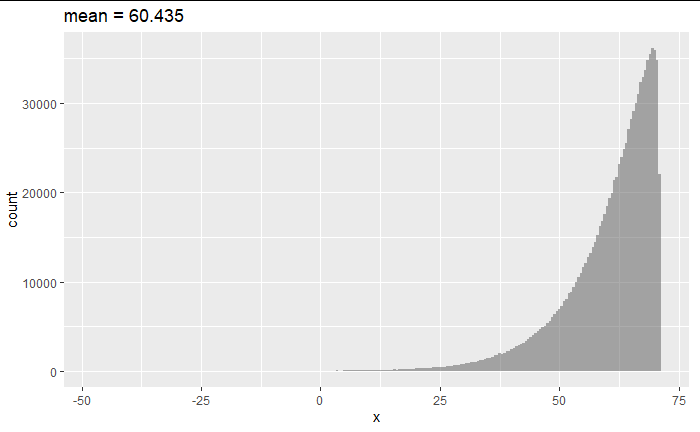
data<-data.frame(x = rgev(1000000,60,10,-0.9))
data %>% ggplot(aes(x = x))+
geom_histogram(binwidth=0.5,alpha = 0.5)+
labs(title = str_c("mean = ",round(mean(data$x),3)))
推測統計の話ならrsampleよりinferの方が楽。
ブートストラップによるサンプリング分布を計算していく。
mu <- mean(data$x)
set.seed(59)
sampling_index <- sample(nrow(data))[1:60]
sample_data <- as.tibble(data[sampling_index,])
bootstrap_data <- sample_data %>%
specify(response = value)%>%
generate(reps = 100000, type = "bootstrap") %>%
calculate(stat = "mean")
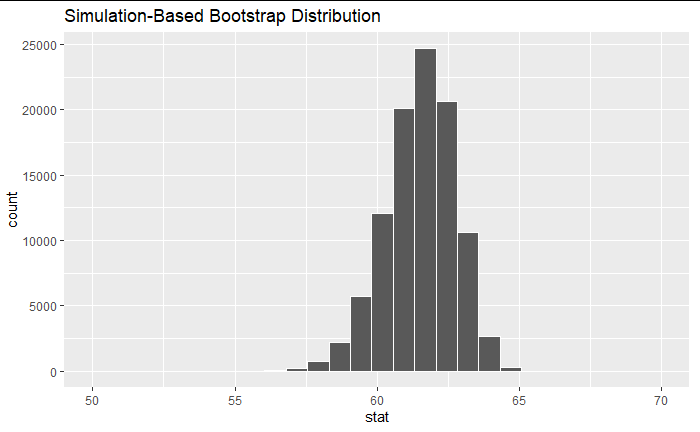
visualise(bootstrap_data)+xlim(50,70)
平均値から正規分布を仮定したら?標準誤差法
standard_error_ci <- bootstrap_data %>%
get_confidence_interval(type = "se", point_estimate = mean(sample_data$value))
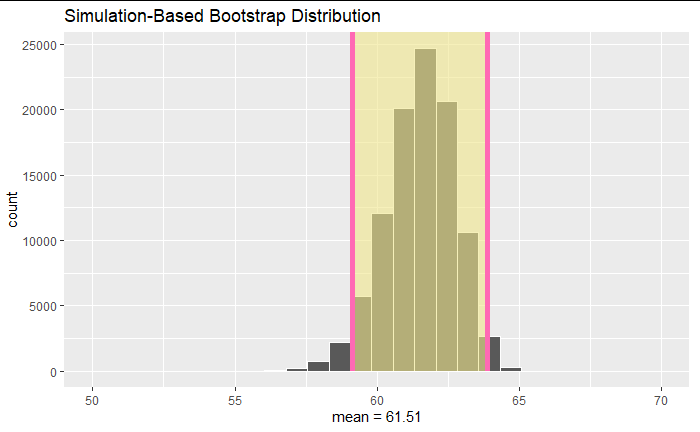
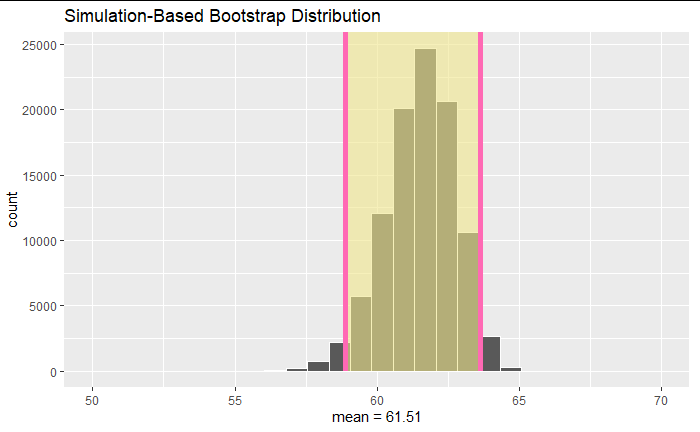
visualise(bootstrap_data)+shade_ci(endpoints = standard_error_ci, color = "hotpink", fill = "khaki")+xlim(50,70)+xlab(str_c("mean = ",round(mean(sample_data$value),2)))
set.seed(1)
mu <- mean(data$x)
for_plot <- NULL
for(o in 1:5){
count=0
for(i in 1:100){
sampling_index <- sample(nrow(data))[1:60]
sample_data <- as.tibble(data[sampling_index,])
repeat_bootstrap_data <- sample_data %>%
specify(response = value)%>%
generate(reps = 100000, type = "bootstrap") %>%
calculate(stat = "mean")
standard_error_ci <- repeat_bootstrap_data %>%
get_confidence_interval(type = "se", point_estimate = mean(sample_data$value),level = 0.95)
if((mu > standard_error_ci$lower_ci & standard_error_ci$upper_ci > mu)== TRUE){count = count + 1}
if(o==1){
long_repeat_bootstrap_data <- data.frame(data=repeat_bootstrap_data,number=i)
for_plot <- rbind(for_plot,long_repeat_bootstrap_data)
}
}
print(paste("true mean include CI count is ",count))
}
[1] "true mean include CI count is 95"
[1] "true mean include CI count is 93"
[1] "true mean include CI count is 87"
[1] "true mean include CI count is 97"
[1] "true mean include CI count is 87"
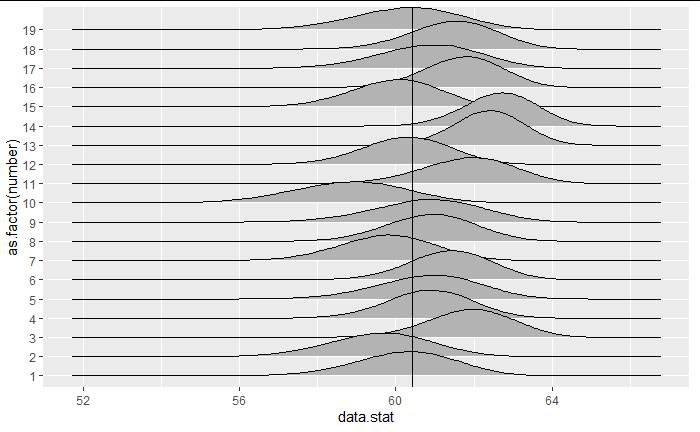
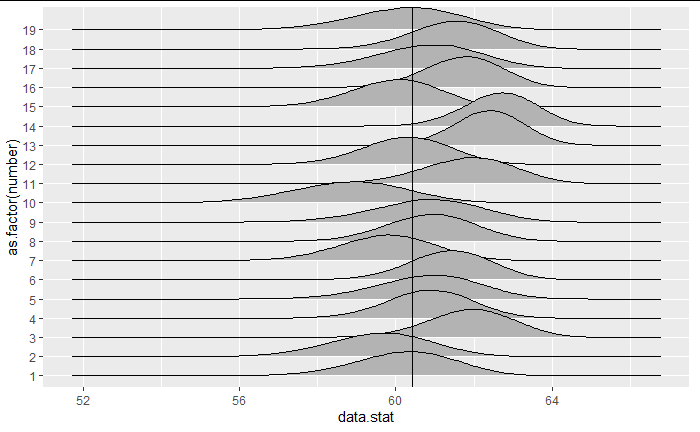
as.tibble(for_plot) %>% filter(number<20) %>% ggplot(aes(x = data.stat, y = as.factor(number))) + geom_density_ridges()+geom_vline(xintercept= mu)
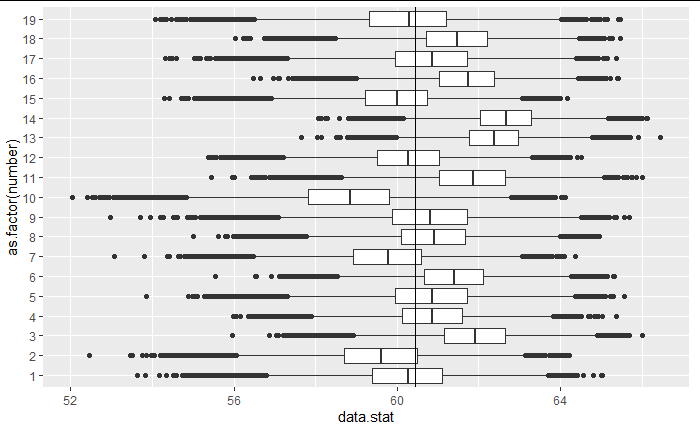
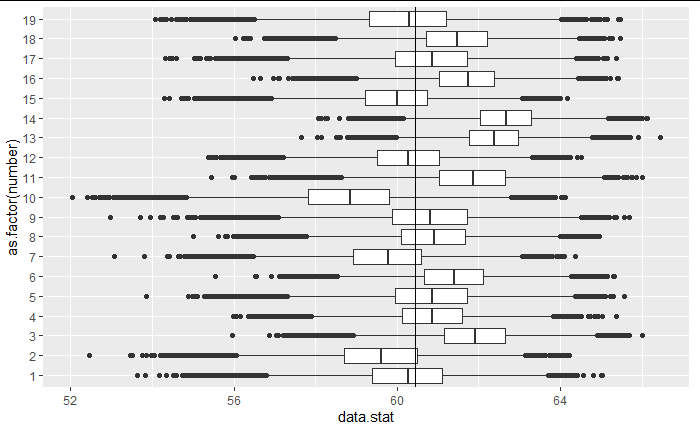
as.tibble(for_plot) %>% filter(number<20) %>% ggplot(aes(x = data.stat, y = as.factor(number)))+ geom_boxplot()+geom_vline(xintercept= mu)
平均値から正規分布を仮定したら?パーセンタイル法
percentile_ci <- bootstrap_data %>%
get_confidence_interval(level = 0.95, type = "percentile")
visualise(bootstrap_data)+shade_ci(endpoints = percentile_ci, color = "hotpink", fill = "khaki")+xlim(50,70)+xlab(str_c("mean = ",round(mean(sample_data$value),2)))
set.seed(1)
mu <- mean(data$x)
for_plot <- NULL
for(o in 1:5){
count=0
for(i in 1:100){
sampling_index <- sample(nrow(data))[1:60]
sample_data <- as.tibble(data[sampling_index,])
repeat_bootstrap_data <- sample_data %>%
specify(response = value)%>%
generate(reps = 100000, type = "bootstrap") %>%
calculate(stat = "mean")
percentile_ci <- repeat_bootstrap_data %>%
get_confidence_interval(level = 0.95, type = "percentile")
if((mu > percentile_ci$lower_ci & percentile_ci$upper_ci > mu)== TRUE){count = count + 1}
if(o==1){
long_repeat_bootstrap_data <- data.frame(data=repeat_bootstrap_data,number=i)
for_plot <- rbind(for_plot,long_repeat_bootstrap_data)
}
}
print(paste("true mean include CI count is ",count))
}
[1] "true mean include CI count is 94"
[1] "true mean include CI count is 93"
[1] "true mean include CI count is 89"
[1] "true mean include CI count is 97"
[1] "true mean include CI count is 87"
as.tibble(for_plot) %>% filter(number<20) %>% ggplot(aes(x = data.stat, y = as.factor(number))) + geom_density_ridges()+geom_vline(xintercept= mu)
as.tibble(for_plot) %>% filter(number<20) %>% ggplot(aes(x = data.stat, y = as.factor(number)))+ geom_boxplot()+geom_vline(xintercept= mu)
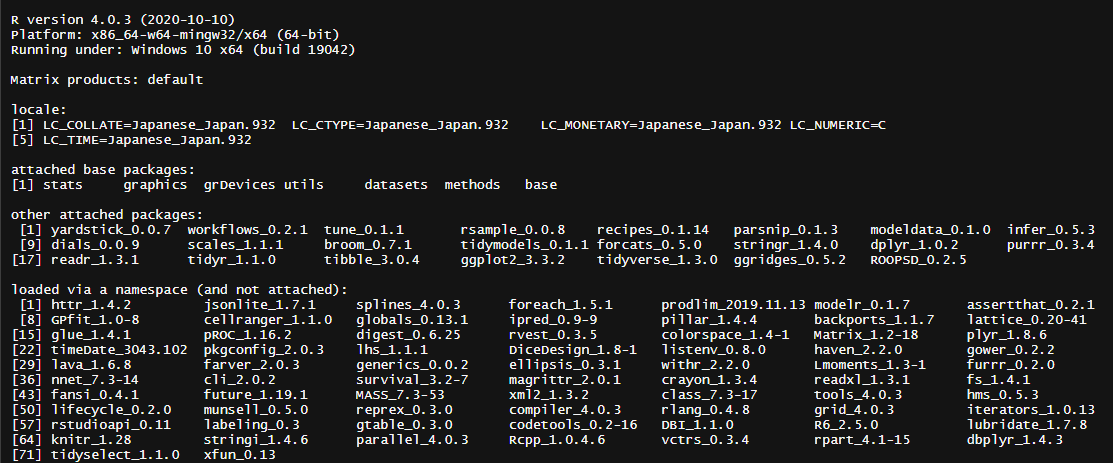
実行環境
資料
An Introduction to the Bootstrap
Statistical Inference via Data Science: A ModernDive into R and the Tidyverse