ごちうさ三期、ご注文はうさぎですか?BLOOMの放送を記念して、tidymodelsのbroomパッケージを紹介する。
ごちうさが無ければこの記事は作られてはいない。
ごちうさに感謝。
日本に戦争が起こっていないのは、ごちうさの続編が生まれなくなるのが一因という説もある。
内容は真面目にプログラミングでいく。
関係する記事としてこちらも書いた。
第一章「モデルの結果を受け取る」
broomパッケージとは、
broomは統計処理の結果をとっても扱いやすくするパッケージ
理解するために扱いにくかった頃の話から始める
単回帰モデルや重回帰モデルを作る時はどうやって実行している?
私はlm()を使っています
library(tidyverse)
library(tidymodels)
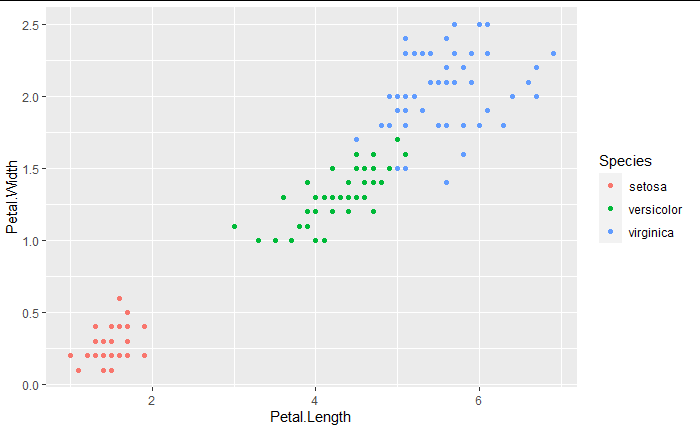
iris %>% ggplot()+
aes(x=Petal.Length,y=Petal.Width)+
geom_point(aes(col=Species))
fit <- lm(Petal.Length ~ Petal.Width, iris)
fit_pred <- data.frame(y=predict(fit, newdata=iris),x=iris$Petal.Width)
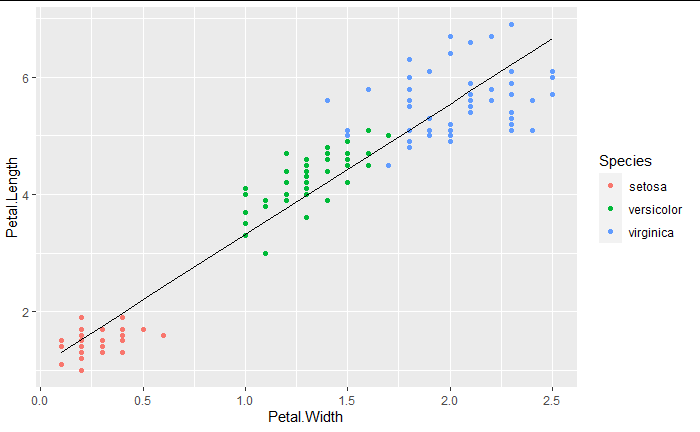
iris %>% ggplot()+
aes(y=Petal.Length,x=Petal.Width)+
geom_point(aes(col=Species))+
geom_line(aes(x=fit_pred$x,y=fit_pred$y))
じゃあモデルの係数を確認したい時はどする?
私はfitしたmodelを確認するか、summary(model)を使っています
fit
Call:
lm(formula = Petal.Length ~ Petal.Width, data = iris)
Coefficients:
(Intercept) Petal.Width
1.084 2.230
result <- summary(fit)
result
Call:
lm(formula = Petal.Length ~ Petal.Width, data = iris)
Residuals:
Min 1Q Median 3Q Max
-1.33542 -0.30347 -0.02955 0.25776 1.39453
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.08356 0.07297 14.85 <2e-16 ***
Petal.Width 2.22994 0.05140 43.39 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.4782 on 148 degrees of freedom
Multiple R-squared: 0.9271, Adjusted R-squared: 0.9266
F-statistic: 1882 on 1 and 148 DF, p-value: < 2.2e-16
じゃあ係数をデータとして取り出す時は?
modelの型を調べてみるとlistだから番号を振ったら取り出せるかもしれない
listの要素に名前が付いているかも確認してみる
mode(fit)
[1] "list"
names(fit)
[1] "coefficients" "residuals" "effects" "rank" "fitted.values" "assign" "qr" "df.residual" "xlevels"
[10] "call" "terms" "model"
実はmodelの中に12個も要素が詰まっていることが分かった。
中でも今回は係数であるcoefficientsを取り出すには
data.frame(fit$coefficients)
fit.coefficients
<dbl>
(Intercept) 1.083558
Petal.Width 2.229940
こうしてやれば取り出せる。
じゃあp値を取り出したい場合は?
訓練データにfitした値は?
F値は?
自由度は?
これらを取り出すためには各々の要素を探し出して指定して、再度data.frame型に変換する必要がある。
summaryの場合にも複数個の要素が複雑に格納されているので、一つ一つの要素に対して別々の操作をするのは大変。
result <- summary(fit)
for(i in 1:10){
print(paste("result",i,"th content"))
print(result[i])
}
訓練データにfitした値を描画するための変換をしてみる
fit <- lm(Petal.Length ~ Petal.Width, iris)
fit_value = data.frame(fit_val=fit$fitted.values)
iris %>% ggplot()+
aes(y=Petal.Length,x=Petal.Width)+
geom_point(aes(col=Species))+
geom_line(aes(x=fit_pred$x,y=fit_value$fit_val))
この場合fit_valueにx軸の値が入らないので別で取得しておく必要がある。
まだx,yだけを指定したらよかったが、より複雑な手順を踏むときにこんなことをしているとミスが発生する。
そこでbroom
broomにはtidy,glance,augmentの大きく三つの関数が存在しているのでこれを説明してみる
係数の情報を取り出したいときにはtidy()で一発
fit %>% tidy()
p値なども含めてテーブル形式に結果を得られる。
テーブルというかtidyverseでもおなじみのtibble型。
さらに、summaryやmodel自体を確認した場合、coefficientの結果は行名にInterceptなどが入っていたが、tidy系パッケージの考え方として、各行の属性を表すデータは縦に一列に存在しているべきという考えなので行名が列になっている。
fit %>% glance()
glanceではモデルの比較時に役立つようなAIC,決定係数、などをtibbleとして取得することができる。
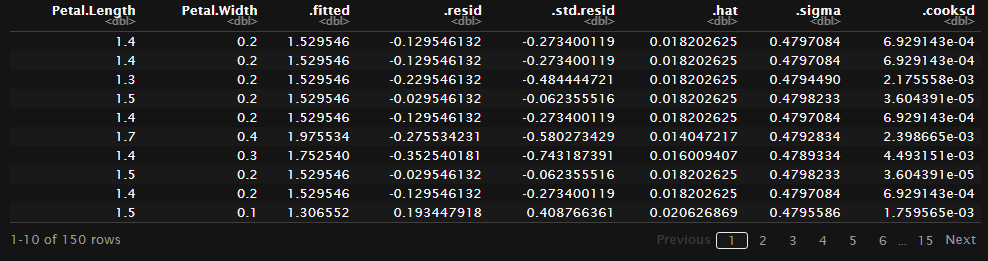
fit %>% augment()
augmentはfitデータとfit結果を横に結合して保有してくれる。
いちいちfitted.valueで取ってこなくてもいい。
fitデータとして指定したx,yだけでなく、元のデータ全てと結合したい場合には
augment(fit,iris)
で元データを付け加える。
このように元データが横に結合した形となることで、先ほどまでで見たようなfit済データの描画が一つのデータフレーム内で完結する。
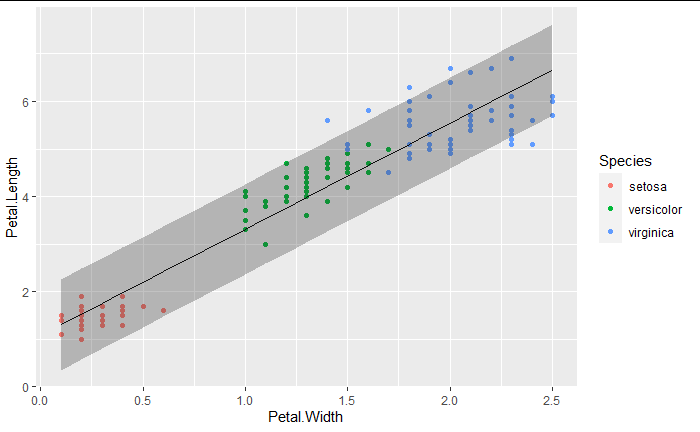
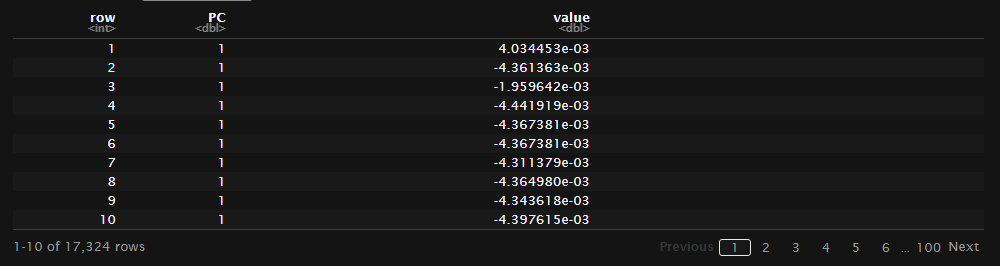
pred_iris <- augment(fit, newdata = iris, interval = "prediction")
pred_iris %>%
ggplot(aes(x=Petal.Width, y=Petal.Length)) +
geom_point(aes(col=Species)) +
geom_line(aes(y = .fitted)) +
geom_ribbon(aes(ymin = .lower, ymax = .upper), col = NA, alpha = 0.3)
第二章「lm以外のtidy()の使い方」
特異値分解の出力結果
たとえば特異値分解をおこなうsvd()という関数がある。
この出力はリストの中に次元の異なるリストが入れ子に存在する形になっている。
library(modeldata)
data(hpc_data)
mat <- scale(as.matrix(hpc_data[, 2:5]))
s <- svd(mat)
s
繰り返すが、tidy系一つの要素は一つのテーブルで所有すべきという考えなので、このような構造は望ましくない。
svd()の出力に対してもtidy()が対応するように設計されている。
svd()の出力はv,u,dの三種類のマトリックスが格納される。
tidy(s,matrix="u")
tidy(s,matrix="d")
tidy(s,matrix="v")
複雑で確認に労力を使うような結果がtibbleとして綺麗に整頓されて帰ってくるのは気持ちがいい。
時系列モデルの出力結果
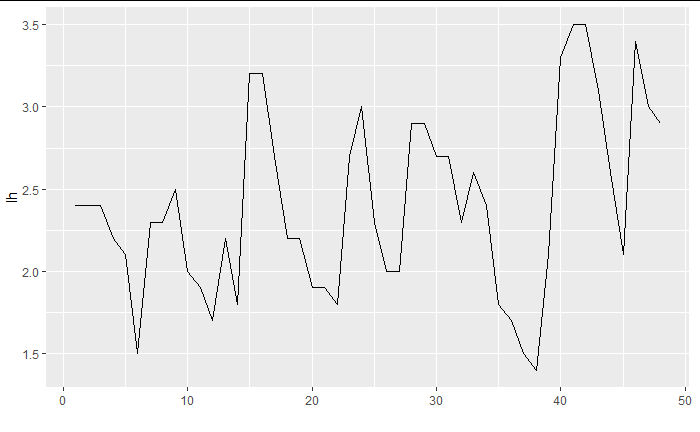
時系列データに対してモデリングをしてみよう
data.frame(lh) %>% mutate(row_index=row_number()) %>% ggplot(aes(x=row_index, y=lh)) +
geom_line() +
xlab("")
fit_arima <- arima(lh, order = c(1, 0, 0))
fit_arima
Call:
arima(x = lh, order = c(1, 0, 0))
Coefficients:
ar1 intercept
0.5739 2.4133
s.e. 0.1161 0.1466
sigma^2 estimated as 0.1975: log likelihood = -29.38, aic = 64.76
モデルは上記のように1次のAR(1)を仮定してfitさせた。
時系列モデルの出力結果はlmの結果ともまた異なる。
AR(1)の係数が左列に、interceptが右列に存在している。
係数がlmのように横に記述されていない。
tidy()はこれもフォローしている。
tidy(fit_arima)
パッケージ(関数)間での出力形式が統一的でなかった今までに対して、tidy()が出力結果を一貫した形へと管理してくれる。
これがtidy()のアリガタイところ。
検定の結果
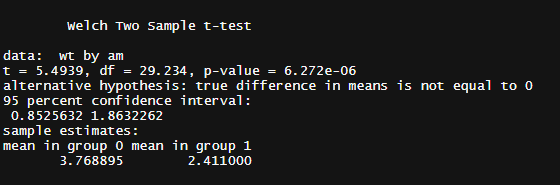
たとえばt-testを行った場合
tt <- t.test(wt ~ am, mtcars)
tt
またも取り出すために労力が必要そうな結果だが、
tidy(tt)
tidyがtibbleとして取り出すことを補助してくれる。
t.testに限らず複数の検定に対応できるような実装がされている。
データの要約統計量を得るためにtidy()を使う
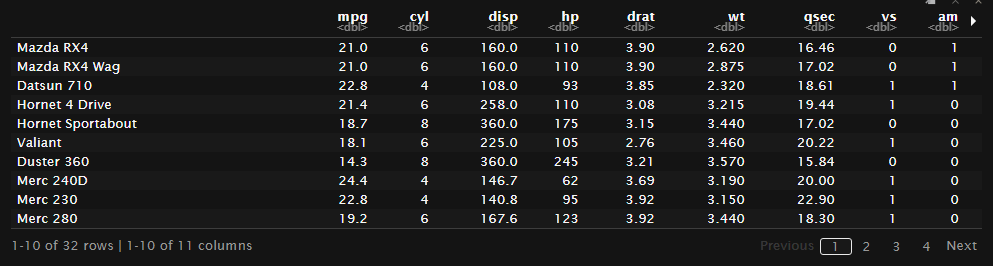
何度かtidyなデータテーブルの話をしたが、mtcarはtidyでないテーブルデータである
mtcars
行名にデータの属性が入ってしまっている。
列の中にデータが入れ子になっていないだけまだtidyな部類のデータかもしれない。
このように属性(factor,character列)の無いデータに対してtidy()を使用すると要約統計量を返してくれる。
tidy(mtcars)
tidy(iris %>% select(-Species))
※この機能はいずれ削除される機能になっている様子
そのため近そうな機能としてskimrの中身を取り出す場合を紹介しておく。
全く同じ結果ではないが、似たことは実現できる。
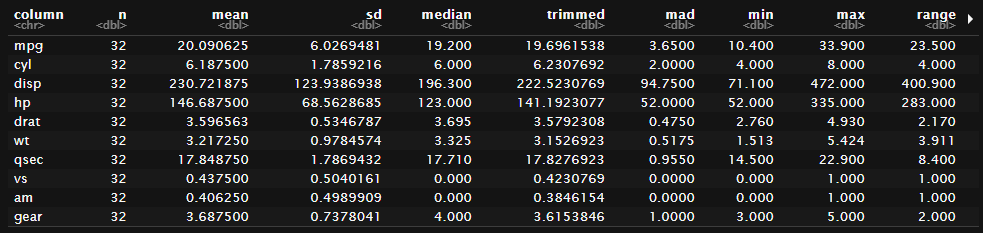
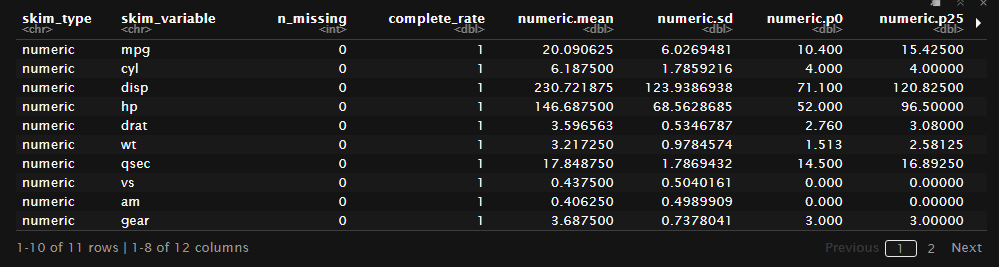
library(skimr)
skim_object <-skim(mtcars)
tibble(skim_object)
混同行列のtidy化
library(modeldata)
library(caret)
data("two_class_example")
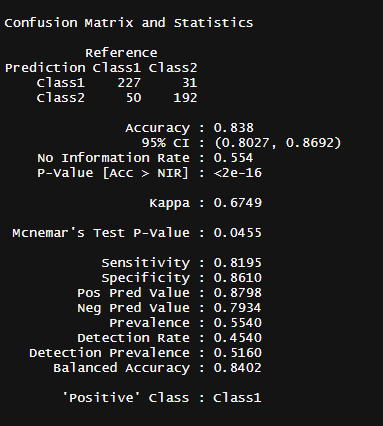
two_class_cm <- caret::confusionMatrix(
two_class_example$truth,
two_class_example$predicted
)
これまた取り出しにくい情報。
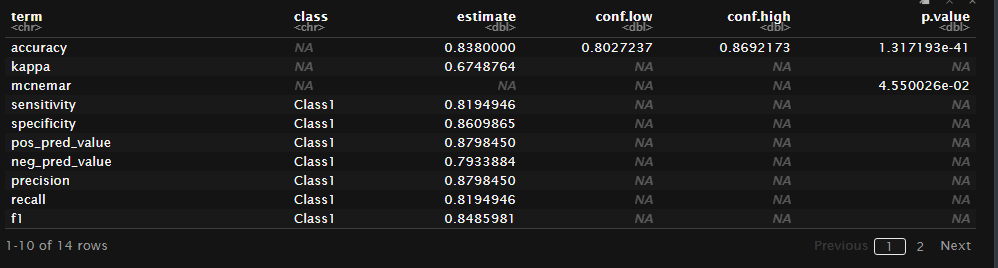
tidy()なら?
より確認しやすい形式で表示できる。
その他
今までtidy()が扱いやすくしてくれる様々な統計処理の結果を紹介してきたが、ほんの一部であり、
coeftestやwilcox.test,Kendall,TukeyHSD,anova,acf,pacfなどなど、
ここに記入できないほどに複数の出力をサポートしてくれている。
もし、いつも扱っているパッケージの結果が上記で紹介したような扱いにくい場合にはbroomのリファレンスを調べてみることをオススメする。
第三章「tidy()とmodeling」
最後にrsampleとbroomの便利な関係を紹介しておく。
たとえbootstrap法によって係数のサンプリング分布を得たい時や、
交差検証のデータセットによって、どれだけモデルが変化するのかを確認したいときにtidyは役に立つ。
purrrのmapやtidyrのnestについては別記事を参照してほしい。
(いずれ書く。それまでは他ブログで。)
まずブートストラップ標本を作る
試しに20個作ってみよう
boots <- bootstraps(iris, times = 20, apparent = TRUE)
fit_analysis <- function(split) {
model <- lm(Petal.Length ~ Petal.Width , analysis(split))
}
mapは簡単に説明すると、複数のリストに対して順番に処理をかけていく処理を行う。
pythonでlist内包表記に慣れているひとはそれを想像してもらえれば概念的に近い。
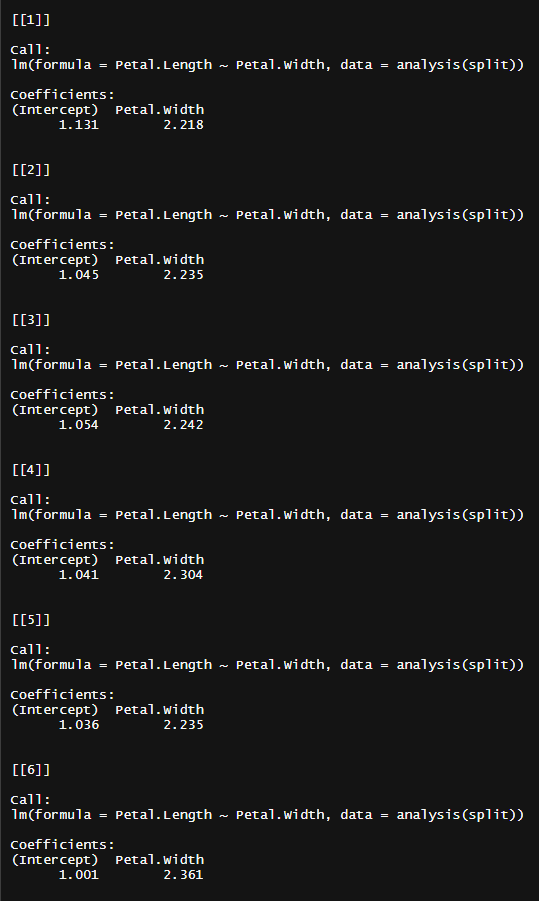
map(boots$splits, fit_analysis)
rsampleのbootstrap()はブートストラップ標本を作り出し、id列とsplits列を作る。
id列は何番目のブートストラップ標本かを表し、splits列はブートストラップ標本のデータフレーム(tibble)を入れ子状にして持つ。
tidyなデータに反しているように思われるかもしれないが、一つのセルに対して一つのデータフレームというデータが格納されているので思想的に問題はない。
この一つ一つのデータはanalysis()で展開することができる。
rsampleでは余計なデータをメモリの中に納めないように元データのインデックスだけを持つので訓練するためには展開してやる必要がある。
ちなみにbootstrap法を知っている人は余ったデータ(out of bag)があることはご存じだと思うが、これはassessment()で取り出すことができる。
analysis(boots$splits[[1]])
assessment(boots$splits[[1]])
このようにして得た各ブートストラップ標本ごとのモデルは、それぞれ係数の推定値を持つことになる。
この係数の推定値について0と比較し検定を行うのが「回帰係数の検定」なわけだが、この統計的な考え方が分かりづらい。
そこで「ブートストラップ法によって統計量のサンプリング分布を生成して、その分布の95%信頼区間内に0が無ければ0とは言えないだろう」
と考える。
現代のコンピュータなら理論的な話でなく、データを元にしたシミュレーションを計算機の力で実現させることができる。
そして、各モデルから係数の推定値を取り出す時に便利にしてくれるのが「broom::tidy()」であった。
これを各モデルに対してmapで処理をかける
boot_models <-
boots %>%
mutate(model = map(splits, fit_analysis),
model_contents_tidy = map(model, tidy))
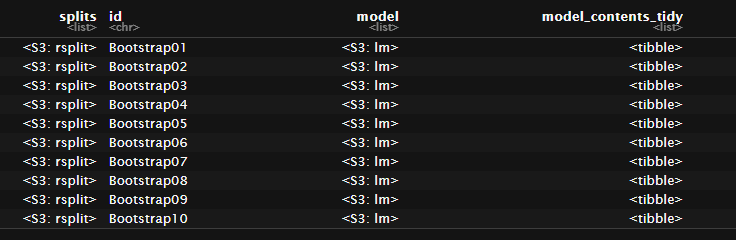
boot_models
各nestに圧縮されたブートストラップ標本にモデルを適応させ、モデル出力はnmap()によってnest()で入れ子にされている。
これをさらにmap()でtidy()処理することで係数の推定値などのtibbleが得られ、このtibbleもまたnest()されて一つ一つのセルに圧縮されている。
では係数の推定値たちのnestをunnest()で解除してやろう。
boot_estimate <-
boot_models %>%
unnest(model_contents_tidy)
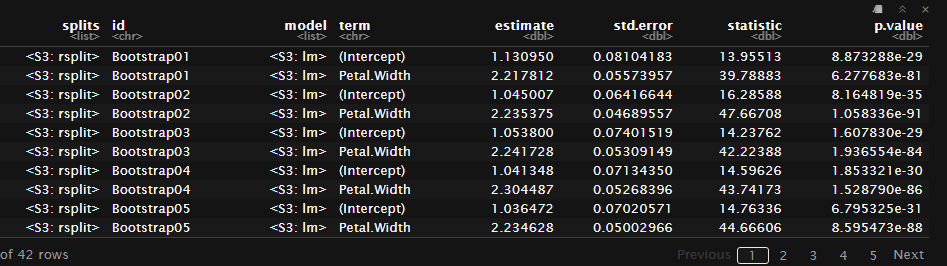
boot_estimate
切片とPetal.Widthの係数が確認できる。
このPetal.Widthの係数のみを取り出し、ブートストラップ分布を作ってみる。
boot_estimate <- boot_estimate %>% mutate(fct_column = as.numeric(factor(term)))
# factorの番号を確認
# boot_estimate %>% select(term, fct_column)
pet_wid <- boot_estimate %>% filter(fct_column == 2) %>% select(term,estimate,id)
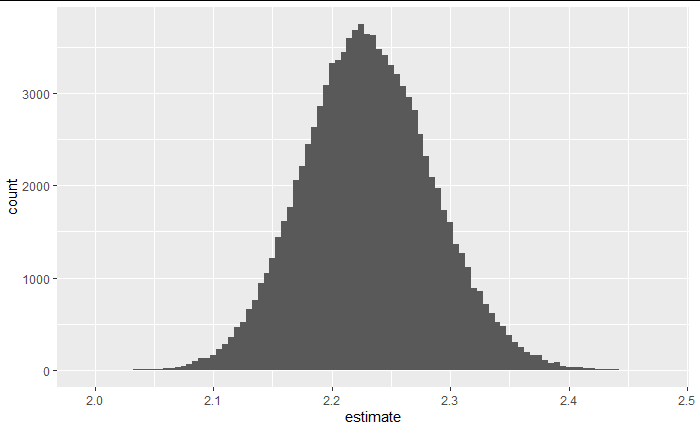
pet_wid%>% ggplot()+
aes(x=estimate)+
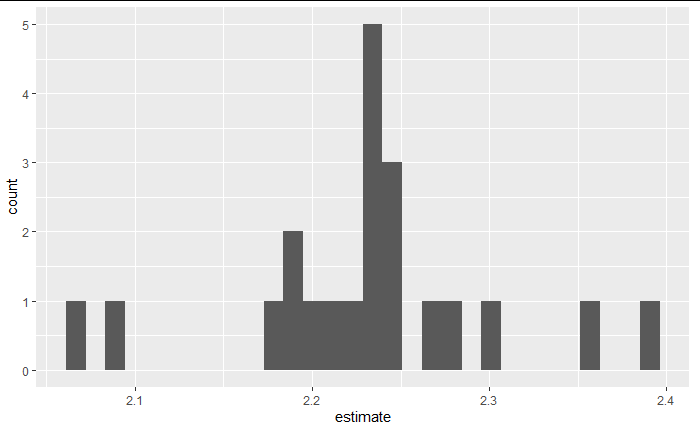
geom_histogram()
このようにestimateの分布を得ることができた。
標本数を増やすことで
このように分布らしくなる。
この結果から、たまたま偶然係数が大きく出たわけではないという事が考察できる。
(ブートストラップ分布のばらつきはサンプリング分布のバラツキと似た値なため)
さて、この繰り返し処理で活躍するのはtidy()だけではない。
augment()を思い出してみると、fitした後の値を元データと共に保存することの出来る関数だった。
つまり、各ブートストラップ標本ごとに異なったモデルが得られ、そのモデルのfit後の値も展開できるので、
boot_data <-
boots %>%
mutate(model = map(splits, fit_analysis),
model_augment = map(model, augment))
boot_data %>% unnest(model_augment)
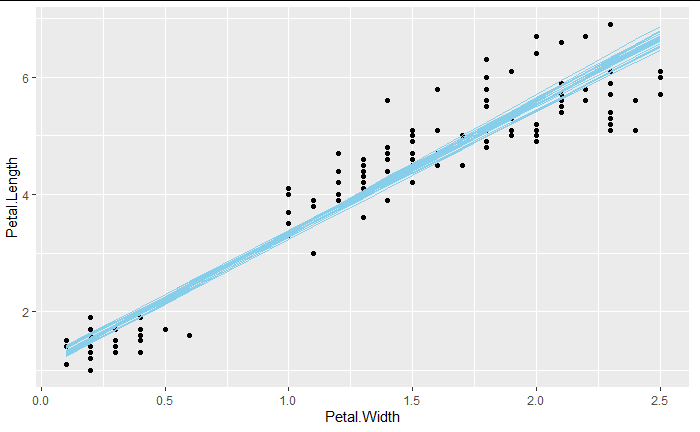
boot_data %>% unnest(model_augment) %>%
ggplot(aes(x=Petal.Width, y=Petal.Length)) +
geom_point() +
geom_line(aes(y = .fitted, group = id),col="skyblue")
このように、現在のモデルのバイアス・バリアンスを議論することができるようになる。
今のモデルがあまりにも過適合しやすいとわかったならば、係数の検定以前にアルゴリズム選択の時点からやり直すことができる。
以上
tidymodelsのbroomべんり、って話でした。
tidymodelsのrsampleとちょこっとinferについても記事を作っているのでそちらもヨロシクどうぞ。
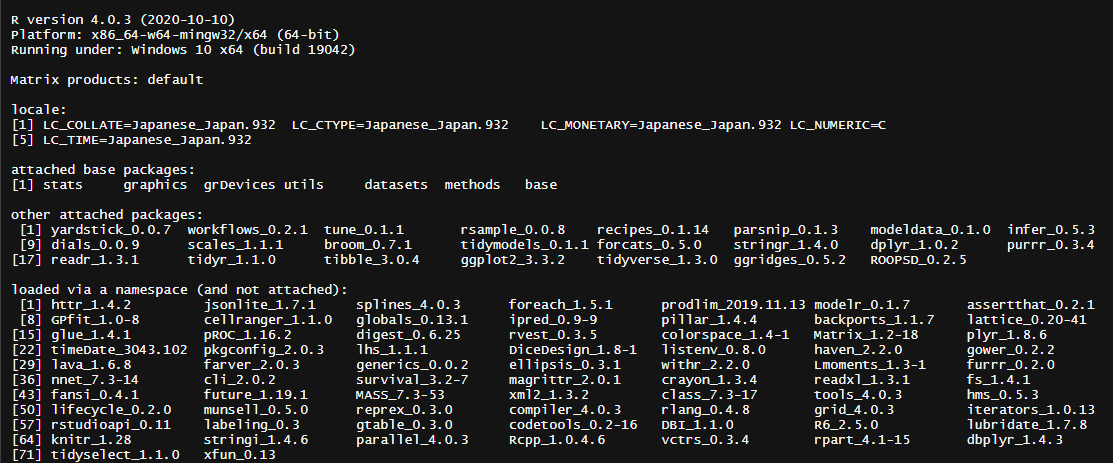
実行環境
資料紹介
Introduction to broom
Tidy a(n) confusionMatrix object
Tidy a(n) Arima object
Augment data with information from a(n) lm object
Tidy a(n) svd object masquerading as list
tidymodels/broom