はじめに
論文名：’Squeeze-and-Excitation Networks’(https://arxiv.org/pdf/1709.01507v3.pdf)
著者：Jie Hu,Li Shen,Samuel Albanie,Gang Sun,Enhua Wu
公開日：25 Oct 2018
参考：
1.https://towardsdatascience.com/squeeze-and-excitation-networks-9ef5e71eacd7
2.https://qiita.com/daisukelab/items/0ec936744d1b0fd8d523
そもそもSENetとは
SEブロックと他のネットワークを組み合わせたもの
モチベーション
畳み込み層に手を加え、パラメータ数と計算量の削減・表現力の向上を目指す
（軽量化によってさらに層を重ねることが可能になり、精度向上にも繋がる）
論旨
何をするのか？
CNNは空間情報とチャンネル情報の2つを合わせて特徴を捉えている
そのうちのチャンネル情報に焦点をあて、CNNの特徴マップのチャンネルを重みづけする
通常の畳み込み層では各チャンネルが均等に出力されるが、それを重み付けすることで情報価値の高いものを強調して比較的価値の低いものを抑える（=表現の質を上げる！）
※空間・チャンネル情報の畳み込みについては「補足：depthwise/pointwise convolution」を参照
従来の手法との違い
従来の手法は空間情報に着目したものが多く、計算も複雑で計算量が大きいものが多い（らしい）
SEブロックは非常に単純で、既存のモデルに追加するだけで性能を大幅に改善できるうえ、
追加計算も非常に少ない（計算量の増加は1%以下！）
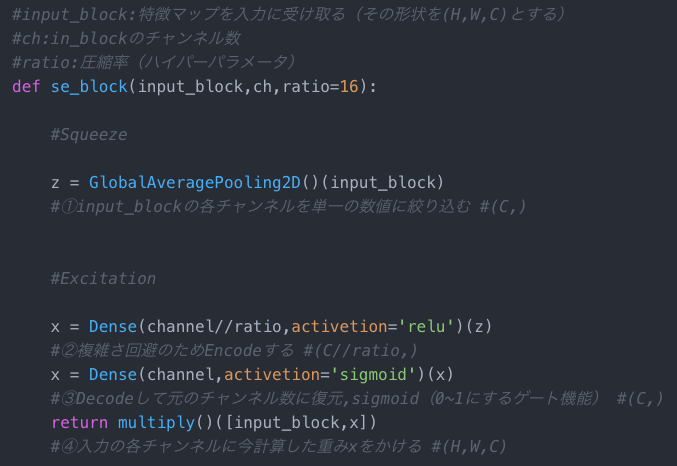
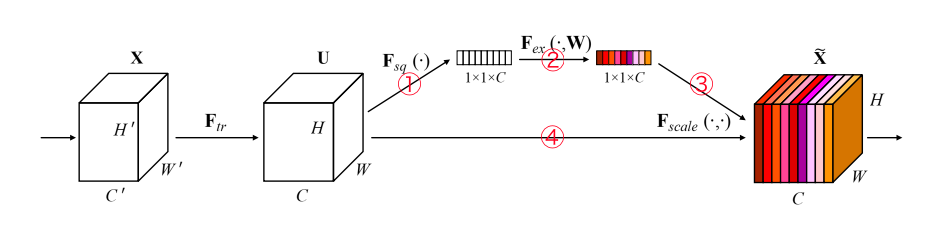
提案手法
SEブロックの実装からその働きを見てみます
①input_blockの各チャンネルを単一の数値に絞り込む
（空間方向に）画像全体の画素値の平均をとり、各チャンネルを単一の数値に変換
チャンネル方向について、局所的な情報だけでなくグローバルな情報を捉えるため
②複雑さ回避のためEncodeする
Encodeすることで複雑化を制限（=一般化）
③Decodeして元のチャンネル数に復元,sigmoid（0~1にするゲート機能）
チャンネル間の相関を捉えるための基準として
1.非線形な相互作用を表現できる
2.one-hotのような排他的な重み付けではなく、複数のチャンネルを重み付けできる
この２つを満たすsigmoidをゲートに利用
④入力の各チャンネルに今計算した重みxをかける
①~③で計算した重みとinput_blockをかける（=input_blockのチャンネルを重み付けする）
SENetの例
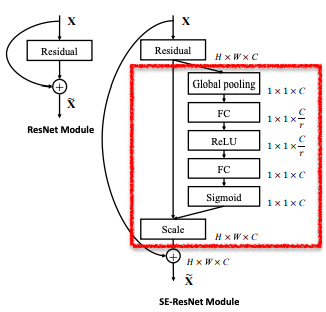
Inceptionとの組み合わせ
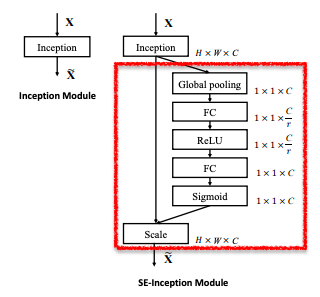
左図（Inceptionモジュール）を元としてSEブロック（赤枠部分）を加えたものが右図
ResNetとの組み合わせ
残差接続があってもSEブロックを付け加えるだけで実装可能
実験結果
ImageNetのデータセットを利用した実験結果
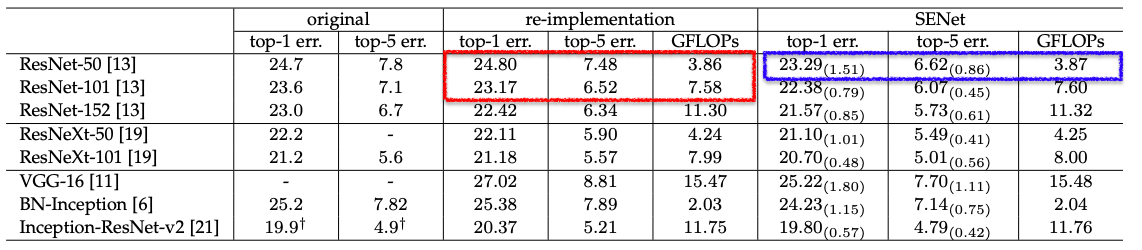
original：元の論文で報告された結果
re-implementation：originalを再訓練したもの（比較で公平性を保つため）
SENet：SEブロックを追加したモデル
ここでは代表例としてSEブロックを追加したResNet-50（青枠部分）を見てみます
計算量（GFLOPsは計算コストの単位）はResNet-50とほぼ変わりませんが（0.26%の増加）
性能はResNet-101を超える精度を持っていることが分かります
補足：depthwise/pointwise convolution
参考：
3.http://deeplearning.hatenablog.com/entry/slicenet
4.https://qiita.com/yu4u/items/34cd33b944d8bdca142d
SENetのチャンネル情報の抽出やそれによる計算量の削減について、特にpointwise畳み込みの考え方が似ていて分かりやすかったので補足として挙げます
depthwise畳み込み
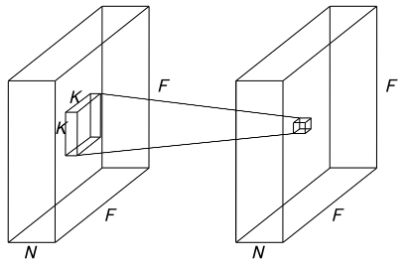
チャンネルに対して独立で、空間情報のみを抽出
入力：（F,F,N）
フィルタ：(K,K,1)
出力：(F,F,N)
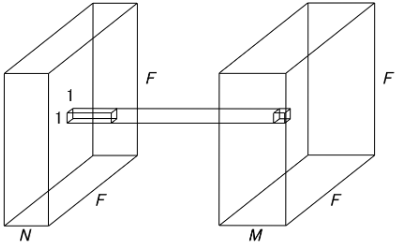
pointwise畳み込み
空間に対して独立で、チャンネル情報のみを抽出
入力：(F,F,N)
フィルタ：(1,1,N）
出力：(F,F,M)
計算量の違い
（計算量ついては参考4がとても分かりやすいです）
通常の畳み込みをpw・dw畳み込みの2つで置き換えるとどのくらい計算量を削減できるのか
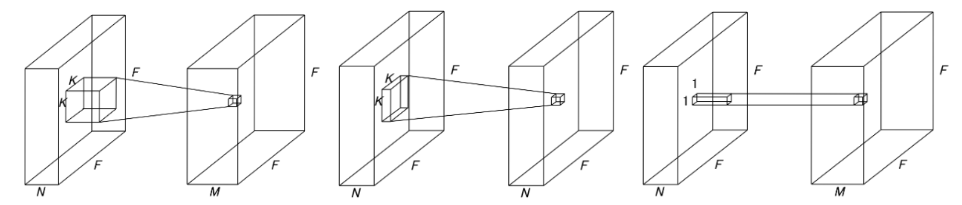
左から通常の畳み込み・dw畳み込み・pw畳み込み（dwとpwは再掲）
通常の畳み込み
→フィルタ１つにつき、コスト$NK^2$の計算を$F^2$箇所で計算
→計算量：$F^2NK^2M$ パラメータ：$NK^2M$
dw畳み込み
→フィルタ１つにつき、コスト$1*(K^2)$の計算を$F^2$箇所で計算
→計算量：$F^2NK^2$ パラメータ：$NK^2$
pw畳み込み
→フィルタ１つにつき、コスト $N*(1^2)$ の計算を $F^2$ 箇所で計算
→計算量：$F^2NM$ パラメータ：$NM$
通常の畳み込みをdwとpwに置き換えることで
計算量：$F^2NK^2M$ → $F^2N(K^2+M)$
パラメータ：$NK^2M$ → $N(K^2+M)$
に削減することが出来る
計算比率は $F^2N(K^2+M)/$$F^2NK^2M$ = $1/M + 1/K^2$
Kはフィルタのサイズなので通常$K=3$または$K=5$
Mはフィルタの数（出力のチャンネル数）なので通常$M>=32$
以上から多くの場合$M>>K^2$ → $1/K^2>>1/M$となるので、
計算量を$1/K^2$と近似して考えると概ね$1/9$から$1/25$程度に削減できるとわかる
ちなみに
SE = Squeeze（圧搾）& Excitation（励起）
圧搾→各チャンネルを単一の数値に変換〔ぎゅっと絞る〕
励起→各チャンネル〔基底状態〕を
相関関係に基づく重み付け〔外場〕によって
重要度を高める〔励起状態にする〕
の意かなと