Kerasの作者@fcholletさんのCVPR'17論文XceptionとGoogleのMobileNets論文を読んだ

はじめに

最初は、軽量なConvNetに興味があったのでGoogleから出ているMobileNets ¹ を読んでいたのだが、その過程でCholletさんのXception論文 ² を（後者は今更）読んだので合わせてまとめる。Cholletさんの論文はなんとなくカジュアルな雰囲気がして面白い。
どちらの論文もpointwise convolutionとdepthwise (separable) convoutionを用いて精度を保ちながらCNNのパラメータ数を削減している。すなわち、精度とパラメータ数のトレードオフを改善していると言える。
Xceptionは、パラメータ削減により、同一のパラメータで大規模な画像認識の高精度化を実現し、MobileNetsは、精度を保ちながMobile上での高速な画像認識を実現している。

下記のTweet、見逃していた。

It's official: my paper "Xception: Deep Learning with Depthwise Separable Convolutions" was accepted at CVPR. https://t.co/D876HseFDo

— François Chollet (@fchollet) 2017年3月4日

ネットワークの軽量化

軽量なネットワーク（性能あたりのパラメータ数が少ないネットワーク）を構築することは、計算資源の限られているモバイルやエッジコンピューティングにおいて重要である。また、ネットワークを軽量化することで、その分ネットワークの層を深くしたりすることもできるので、逆に精度改善につながる可能性もある。
軽量なネットワークを実現する方法はいくつかあるが、畳み込み層の構造を工夫することでパラメータ数を削減する手法と、パラメータ自体を圧縮する手法に大別できる。今回の2つの論文は前者に属する。

• 畳み込み層の構造を工夫することでパラメータ数および計算量を削減する手法
  • GoogLeNet (Inception module) ³, ResNet (bottleneck architecture) ⁴, SqueezeNet (fire module) ⁵, MobileNets & Xception (depthwise and pointwise convolution) ^{1 2}
• ネットワークのパラメータを圧縮する手法
  • バイナリ化 ^{6 7}、Pruning ^{8 9}、量子化（直積量子化含む） ^{8 9 10}、ハフマン符号化 ¹⁰

Depthwise convolutionとpointwise convolution

畳み込み層の計算量とパラメータ数

Pointwise convolutionとdepthwise convolutionのメリットを理解するために、まずは通常の畳み込み層の計算量とパラメータ数について考える。下記のnotationは論文と違うので注意。

ある畳み込み層について、入力特徴マップのサイズを$F \times F$、入力チャネル数を$N$、カーネルサイズを$K \times K$、出力チャネル数を$M$とすると、この畳み込み層の計算量は、$F^2 N K^2 M$となる。
これは、入力特徴マップの１箇所につき畳み込みのコストが$K^2 N$で、これを入力特徴マップの$F^2$箇所に適用することで、１チャネルの出力特徴マップが生成されることから、出力特徴マップが$M$個のケースでは上記の計算量になる。
パラメータ数については、パラメータ数が$K^2 N$の畳み込みが$M$種類あるので、$K^2 N M$となる。

この計算量とパラメータ数を畳み込み層の構成を工夫することで削減することがMobileNetsおよびXceptionのキモである。具体的には、通常の畳込みが、特徴マップの空間方向とチャネル方向に同時に畳み込みを行うのに対し、チャネル方向の畳み込み (pointwise convolution) と空間方向の畳み込み (depthwise convolution) を分ける (factorize) ことを行う。

Pointwise convolution

Pointwise convolutionは、ResNet等のskip connectionでも利用される1x1の畳み込みである。空間方向の畳み込みは行わず、チャネル方向への畳込みを行う。特徴マップの次元を増やしたり減らしたりするのにも利用される。
Pointwise convolutionは、通常の畳込みの$K=1$としたものであるので、計算量は$F^2 N M$、パラメータ数は$N M$となる。

Depthwise convolution

Depthwise convolutionは、特徴マップのチャネル毎にそれぞれ空間方向の畳込みを行う。チャネル方向への畳込みを行わないため、通常の畳込み1回のコストが$K^2 N$から$K^2$になるため、畳み込み層の計算量としては$F^2 N K^2$、パラメータ数は$K^2 N$となる。

上記のようなpointwise convolutionおよびdepthwise convolutionを合わせて適用することで、空間方向とチャネル方向を同時に畳み込む通常の畳込み層を、より少ないパラメータおよび計算量で近似することができる。
計算量に関しては、$F^2 N K^2 M$から$F^2 N M + F^2 N K^2$に削減される。比率で言うと、$1/K^2 + 1/M$になっており、通常$M >> K^2$である (e.g. $K=3$, $M \ge 32$) ことから、計算量は1/9程度に削減されることが分かる。また、pointwise convolutionのほうがボトルネックになっていることも分かる。

XceptionとMobileNets

さて、上記の通り、通常の畳み込みの代わりにpointwise convolutionおよびdepthwise convolutionを利用するのがXceptionとMobileNetsである。それぞれのアーキテクチャは下記の通りである（それぞれ論文から引用）。

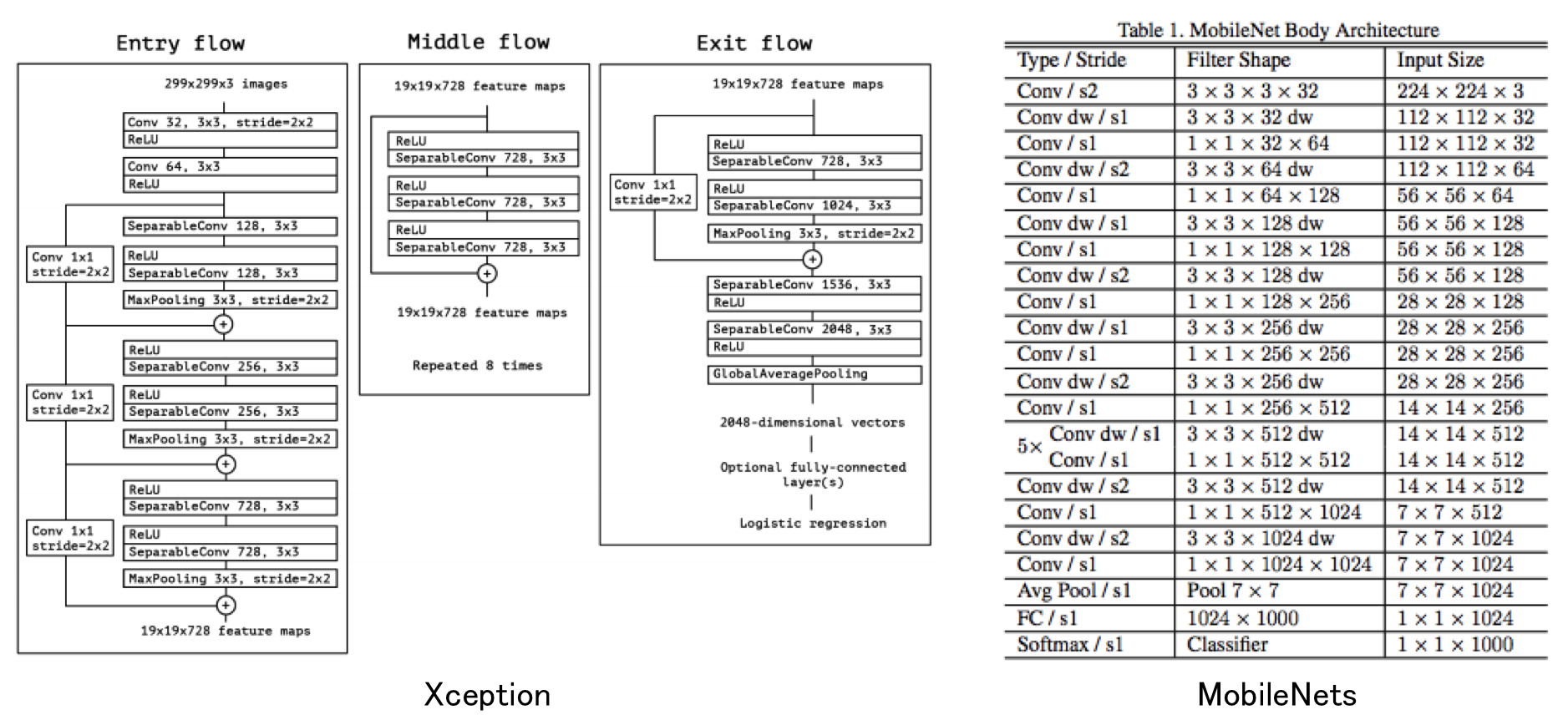
全体を比較しても仕方がないので、モジュール単位で比べてみる。
Xceptionモジュール：
ReLU-depthwise-pointwise-BN-ReLU-depthwise-pointwise-BN-ReLU-depthwise-pointwise-BN（＋identity mapping）
MobileNetsモジュール：
depthwise-BN-ReLU-pointwise-BN-ReLU
となっている。
大きな違いは、

• Xceptionはskip connection (identity mapping) を持っている
• Xceptionはdepthwise convolutionとpointwise convolutionの間に非線形関数が入っていない

の2点である。ちなみにXceptionの元となっているInceptionでは非線形関数は入っている。Cholletさんの考察としては、Inceptionのケースでは、depthwiseに対応する畳み込みはチャネル1の畳み込みを行っているわけではないので、そのようなケースでは非線形性が重要なのでは、とのこと。ちなみに細かいことを言うと、Inceptionモジュールではpointwise convolutionが先に来ている。
個人的にはdepthwise+pointwiseを通常の畳み込み層の代わりと考えるのであればない方が自然な気もするし、それぞれを1つの畳み込みと考えるならば、ResNetのresidual unitのように間にあっても良い気もするので、ケースバイケースなのかもしれない。Skip connectionは多分どんなケースでもあったほうが良いのではないか。

ちなみにMobileNetsは、特徴マップのチャンネル数と入力画像サイズに対し、$\alpha, \rho < 1$のような係数をかけることで、同じネットワークアーキテクチャを利用しながら精度と速度のトレードオフを調節することも提案している。

実験

それぞれそうだろうなぁという結果なので興味があれば見てください（サボり）

余談

ちなみに、Xceptionの論文 ² には、普通は書かないような内部事情に近い細かい話が書いてあるのが面白い。具体的には下記のような内容が事細かに書いてある。

• Depthwise separable convolutionは、2013年にLaurent SifreがGoogle Brainでのインターンで考案し、AlexNetに適用し、精度や収束速度の向上、モデルサイズの削減を実現した。
• 上記の仕事はVincent VanhouckeのICLR'14での招待講演 "Learning visual representations at scale" にて初めて公開された。
• より詳細な実験結果はSifreの博士論文 ¹¹ の6.2章に報告がある。
• Depthwise separable convolutionに関するこの初期の仕事はSifreとMallatのtransformation-invariant scatteringに関する研究 ¹² に着想を得ている。
• 後にdepthwise separable convolutionはInception V1およびV2の最初のレイヤで利用された。
• Google内部では、Andrew HowardがMobileNetsと呼ばれるモバイル向けの効率的なモデルを導入した ¹。

後は、下記ような所属に関する情報が本文に書かれているので、レビュー段階ではどう書かれていたのか気になる。

JFT is an internal Google dataset for large-scale image classification dataset, first introduced by Hinton et al. in [5]...

This evaluation procedure is meant to capture performance on frequently occurring labels from social media, which is crucial for production models at Google.

と思ってarXivの古いバージョンを見たら、下の方の記述は、V2ではat Googleがなかった（最新はV3）。しかしGoogleのInternalデータセットで実験できるのは…

参考文献

---

1. A. G. Howard, M. Zhu, B. Chen, D. Kalenichenko, W. Wang, T. Weyand, M. Andreetto, and H. Adam, "MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications," in arXiv:1704.04861, 2017. ↩

2. F. Chollet, "Xception: Deep Learning with Depthwise Separable Convolutions," in Proc. of CVPR, 2017. ↩

3. C. Szegedy, V. Vanhoucke, S. Ioffe, J. Shlens, Z. Wojna, "Rethinking the Inception Architecture for Computer Vision," in arXiv:1512.00567, 2015. ↩

4. K. He, X. Zhang, S. Ren, and J. Sun, "Deep Residual Learning for Image Recognition," in Proc. of CVPR, 2016. ↩

5. F. N. Iandola, S. Han, M. W. Moskewicz, K. Ashraf, W. J. Dally, K. Keutzer, "SqueezeNet: AlexNet-level accuracy with 50x fewer parameters and <0.5MB model size" ↩

6. M. Courbariaux, Y. Bengio, and J. David, "BinaryConnect: Training Deep Neural Networks with binary weights during propagations," in Proc. of NIPS, 2015. ↩

7. M. Courbariaux, I. Hubara, D. Soudry, R. El-Yaniv, and Y. Bengio, "Binarized Neural Networks: Training Deep Neural Networks with Weights and Activations Constrained to +1 or -1," in arXiv:1602.02830, 2016. ↩

8. S. Han, X. Liu, H. Mao, J. Pu, A. Pedram, M. A. Horowitz, and W. J. Dally, "EIE: Efficient Inference Engine on Compressed Deep Neural Network," in Proc. of ISCA, 2016. ↩

9. S. Han, H. Mao, and W. J. Dally, "Deep Compression: Compressing Deep Neural Networks with Pruning, Trained Quantization and Huffman Coding," in Proc. of ICLR, 2016. ↩

10. Y. Gong, L. Liu, M. Yang, L. Bourdev, "Compressing Deep Convolutional Networks using Vector Quantization," in arXiv:1412.6115, 2014. ↩

11. L. Sifre, "Rigid-motion scattering for image classification, Ph.D. thesis, 2014. ↩

12. L. Sifre and S. Mallat, "Rotation, scaling and deformation invariant scattering for texture discrimination," in Proc. of CVPR, 2013. ↩