前回から 3 年弱が経っているようです汗。
下書きのまま残っているのを偶然見つけたわけです(←おい)。
多分、読み返し前です。いまから読み返しても当時自信がなかったところまで思い出せそうもないので、とりあえず上げちゃいます。
目次
- 導入
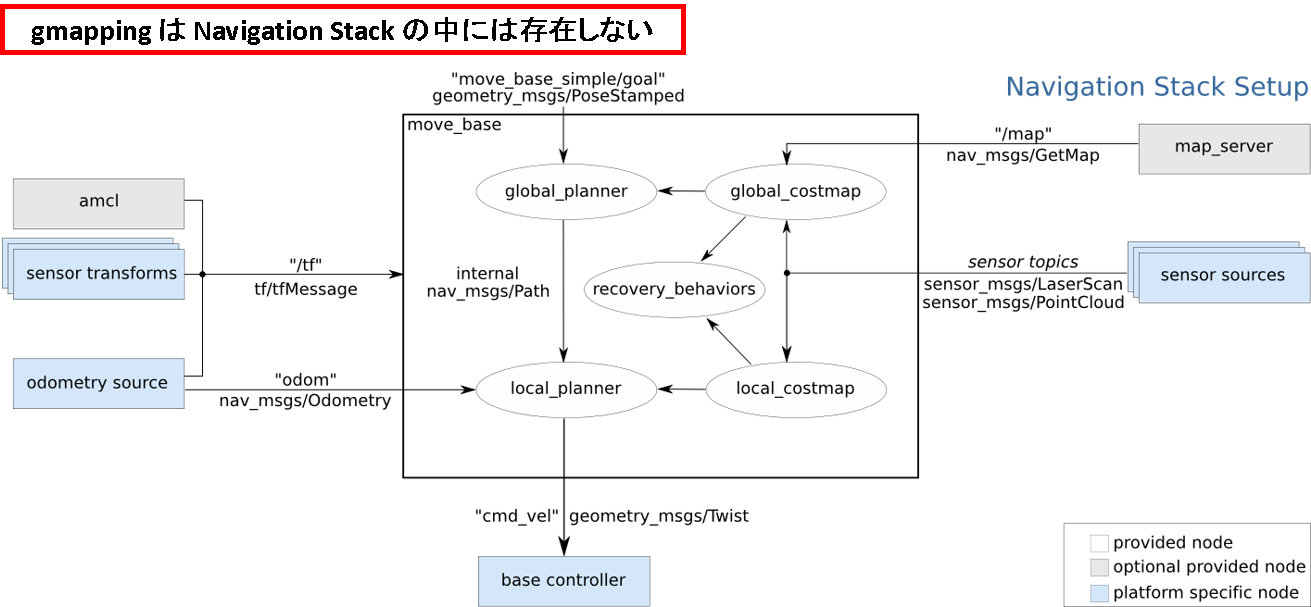
- move_base (ナビゲーション)
- ROSで遊んでみる
- ソフトウェア構成をみる
- amcl (自己位置推定)
- ROSで遊んでみる
- ソフトウェア構成をみる
- 原理をみる (準備編)
- 原理をみる (応用編)
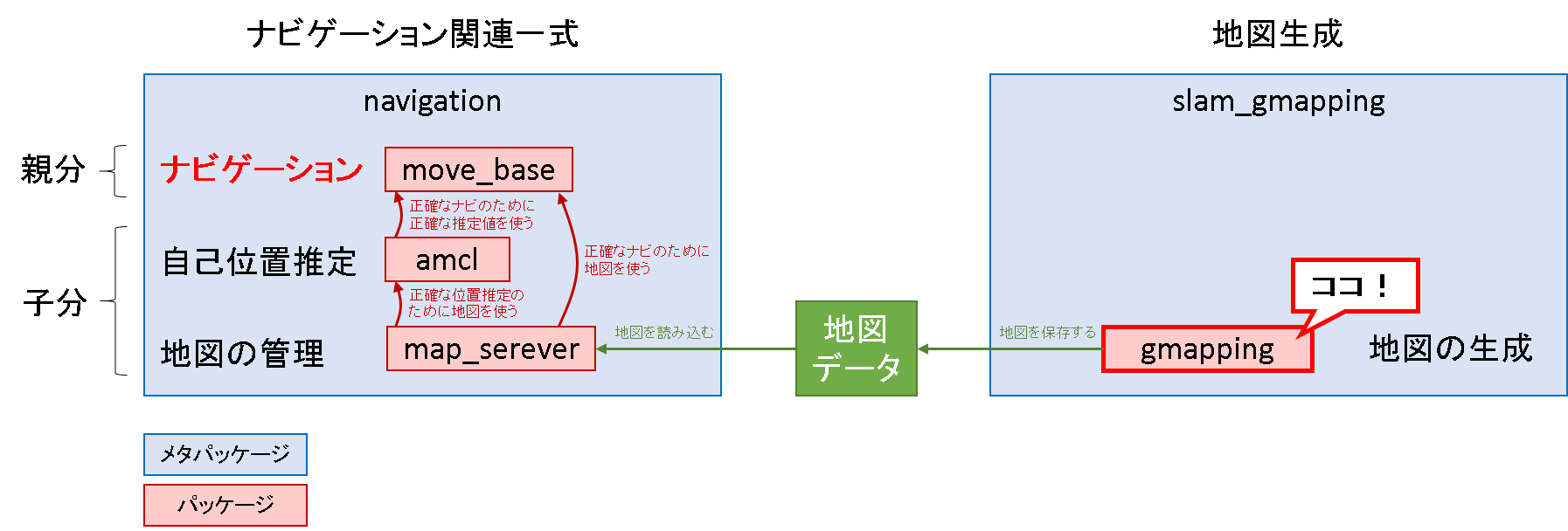
- gmapping (地図生成)
- ROSで遊んでみる
- ソフトウェア構成をみる
- 原理をみる(応用編)
- 原理をみる(準備編 その1) ← いまココ
- 原理をみる(準備編 その2)
はじめに
Navigation Stack を理解する - 4.2 gmapping: ソフトウェア構成をみるの続きです.頑張っているgmappingの中で何が起きているのかを見ていきます.
主に参考とした文献は下記の2です.
- 特徴ベースFast SLAM の基本理論,Rao-Blackwell 化,有占格子地図 等
- 格子ベースFast SLAM の元論文(gmappingはこれを実装),重みの更新式 等
本シリーズでは,数式ガチャガチャのイメージが強いSLAM 問題に必要な技術について,できるだけ数式を排除してイラストを用いて直観的に理解できるように記述することを心がけています.しかし,SLAM 問題に入り込もうと思うと,数式を完全に排除して説明しようとすると雲をつかむような議論となってしまいます.
そこで,本編においては,Fast SLAM で扱う数式と向かい合いながら,その数式の背後にある原理や,それによって実世界での動作に与える影響を考察していくこととします.いわば,Fast SLAM の数式に対するリバースエンジニアリングです.従って,数式の証明自体は追ったりはしません.解析的な証明は,それこそ様々な文献に記述されているので,そちらに譲ることとします.
記述内容は,私の興味の傾向に強く依存するものです.文献で読む範囲で分かりそうだなーと思った内容はここに記述していません.どちらかというと,文献に書いてあることだけでは何言っているか分からないトピックに対して,イラストを試みるイメージです.
当方の性なのですが,「解析的に証明できてるからOK」で終えるとモヤモヤしてダメなんですw そうして得られた結果は必ず空間的であったり,幾何学的に対応させることができるはずだという信念のようなものがあって,そう言う段階まで理解を進めないと先に進みたくないという面倒な性格なのです.
それを今回はSLAMでやっとみようというわけです.前置きはこの辺にして,始めます.
本編の構成
- 準備編 その1
- Fast SLAM の基本フロー
- Rao-Blackwell 化
- 準備編 その2
- オンラインSLAMと完全SLAM
- 有占格子地図
- 応用編
- Fast SLAM 1.0
- Fast SLAM 2.0
- Fast SLAM 1.0 とのイラストによる比較
- Fast SLAM 1.0 との数式による比較(ランドマークベース)
- ランドマークベースから格子ベースへ
本編においても,3.3 amcl: 原理をみる (準備編)と3.4 amcl: 原理をみる (応用編)と同様に,準備編と応用編という順に説明をしていきます.扱うSLAMは,gmapping で実装されているFast SLAM です.
まず準備編では,自己位置推定からSLAMへと展開する上で必要な前提知識について説明をします.ただし,準備編での論点が結構深いので,2部構成とします.応用編ではFast SLAM を例によってイラストを使いながら解釈していきます.
Fast SLAM の基本フロー
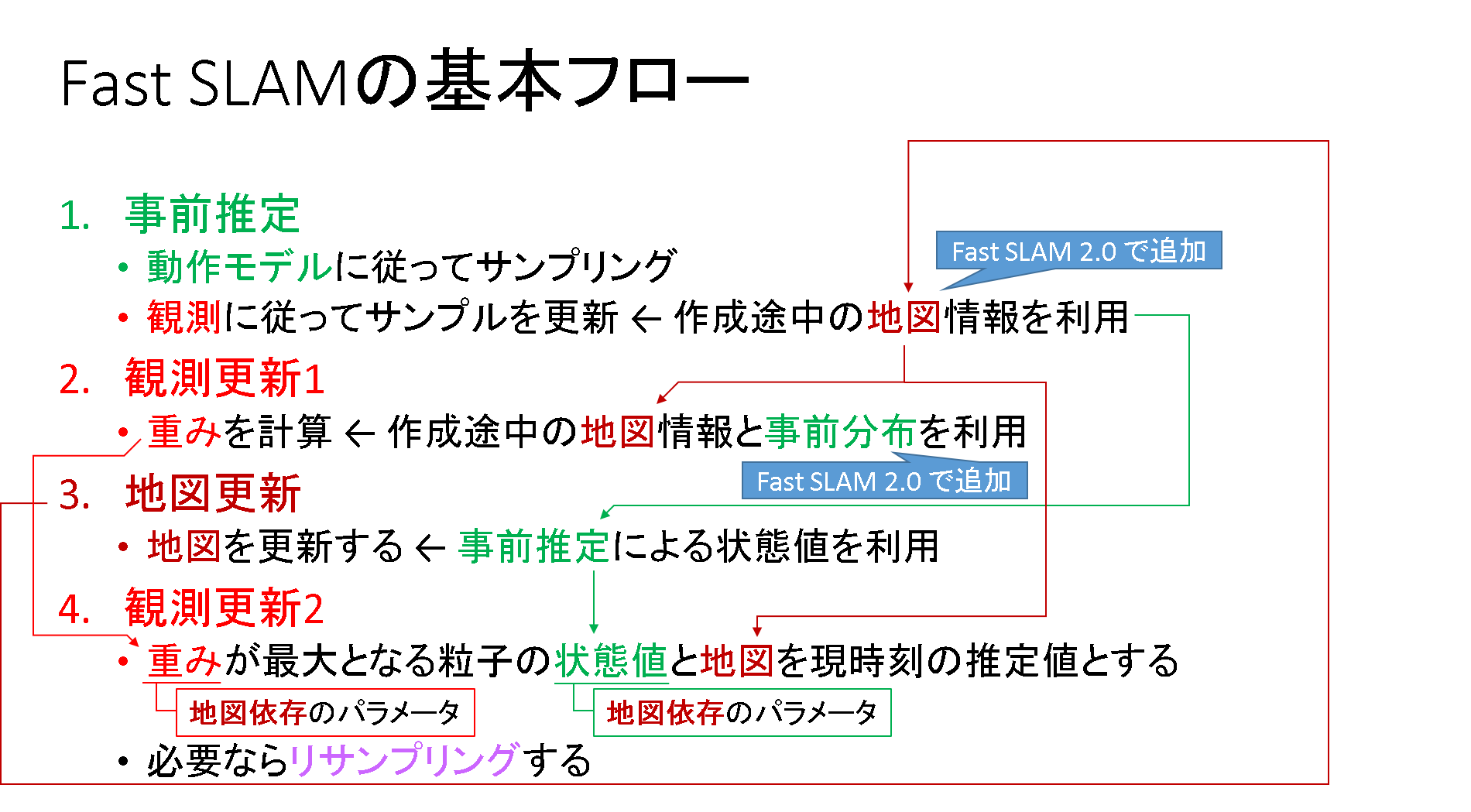
まずはFast SLAM の基本フローを押さえておきます.SLAMのアルゴリズムは長く,ごちゃごちゃとした数式を使うので,「何やら難しそうだ…」という印象を受けてしまいます.私はそう思っていました.ところが,基本的なステップだけを抽出すれば,下記のようなシンプルなものです.
自己位置推定で言うとことの「観測更新」の中ほどに「地図更新」が挿入されただけです.なるほど,当たり前っちゃ当たり前です.何もビビる必要はなさそうです.
隙間の部分を薄くしていた部分に色付けしてみます.
各ステップのフォローは後述することにして,ここでは基本フローの掲載に留めておきます.ただ一点,大事な補足があります.「Fast SLAM 2.0で追加」というコメントが付与されている部分は,「Fast SLAM 1.0」では使わないものとなっています.ここが,Fast SLAM 1.0と2.0との間に潜む決定的な相違点です.詳細は後述することとして,ここでは先に進むこととします.
SLAM に潜む問題点
SLAM は便利で素晴しい技術ですが,過信は危険です.それを簡単に説明します.
下記Fast SLAM 2.0のフローを振り返ります.事前推定,重み計算の際に,観測の情報を使うことになります.この観測情報とのマッチングを行うのは,作成途中の地図です.
あれ,じゃあ地図はそもそもどこから来たんだっけ?となると,これは事前推定で得られた「まだ不確かな状態値」を基に計算されています.つまり,事前推定の誤差がそのまま「地図」の精度にダイレクトに影響するのです.そんな地図を使って次の時刻も事前推定や観測更新を行って,また地図を更新して,というお話を延々と続けるのです.
これはSLAM が原理的に有する問題で,回避は難しいものです.レファレンスとなるものがない状態からスタートさせられて,結局最後まで答え合わせは出来ないのです.せいぜい出来てセルフチェックとカンニング程度です.
例えるならば,何らかの筆記テストを受ける場面を想定します.普通は自分の信念と知識にしたがって回答をします(事前推定).でも,当方は相当な勉強不足なので,その回答にはかなりのばらつきがあって当たるかどうか良くわかりません.でもその途中で,少し戻ってちょいちょい答えの見直しくらいするのは何の問題もありません.そうすることで計算ミス等を見つけられるチャンスくらいはありそうです.ただし,解答はお預け,点数も分からない,自分の出した結論が合っているのか間違っているのかが,真の答えは最後の最後まで分からない,という結構理不尽なテストを受けている状態であると解釈できます.
そんな困った当方に唯一許された答えの確認方法が,カンニング(観測)といったところでしょうか.それが正答なのかどうかは分からないけど,観測された結果と照らし合わせて一致度が高ければ採用できそうだ,というものです(尤度).周りが優秀な人ばかりならよいですが,適当に答えを書いてしまう人だっているかもしれない.この辺りが「センサの信頼度(誤差分散)」に繋がる話になります.ですから,Fast SLAMではLRFやRGBDセンサは優等生であると信じていることを大前提としており,この仮定が崩れると推定精度はガタ落ち必至です.適当に回答した人の答えをカンニングしたって,当てにならなそうですよね笑.
とにかく,Fast SLAMでは本質的に不確かなものだらけの世界で戦う必要があること,事前推定よりも観測情報の方に大きな信頼を寄せているということは,これを利用する上で理解しておく必要がありそうです.
そんな不確かなものを扱っているのだと考えると,パーティクルフィルタを使うことが如何に合理的であるかを余計に理解できます.何もかもが不確かなのだから,とりあえずパーティクルをばら撒きまくって,そこからたまたま尤度が高くなるものが見つかれば万々歳なのです.もちろん当たりの悪いパーティクルもわんさか出るでしょうが,その場合はパーティクルの多様性を失い過ぎない程度にリサンプリングするようチューニングしてしまえばいいんです.
ただし,あんまり適当にばら撒いて尤度の高いパーティクルが見つけられないというのも癪なので,ばら撒き方の指針として「動作モデル」を与えているのです.
更にFast SLAM 2.0 では,事前推定の段階で,より確実に観測尤度の高いパーティクルを得たいがために,わざわざ「事前分布」を近似するパーティクルの位置を「観測更新」によって移動させるような処理まで追加しています.
文献によれば,確かに数式上は問題なく展開されているようなのです.なんか,あの条件付確率の式展開を見ていると,もう何でもありなんじゃないかと思えてきてしまいます笑.
(もちろんそんなことはなく,満たすべき仮定の範疇で数式が展開される必要はあるわけで,それが守られているのは分かるのですが^^; その結論として,「事前推定」の式を「事後推定」の形式に変換できちゃいました!なんていう破壊力抜群の事実を目の当たりにすると,これまで勉強したベイズフィルタの基本式ってなんだったんだろう?と言う感情が湧き出ずにはいられない…^^;)
もういいですね笑.結局,結論はこうです.
- SLAM の基本フローとしては,自己位置推定のフローに「地図更新」のステップが挿入されただけだよ.
- SLAM は便利だけど,地図には推定誤差が載っちゃうし,推定結果にも地図の誤差は載っちゃうで,これは結構大きな問題なんだよ.
- でもそんな未知の環境でも,パーティクルと観測をうまく使えば,そこそこ当てはまりのよさそうな状態推定はできそうなんだよ.センサの精度が良ければね.
と言うことが分かれば,ここは良いかなと思います笑.「簡単に」とか言っておきながら,しょっぱなから色々止まらなくなってしまいました.長文失礼致しました.
Rao-Blackwell 化
なぜRao-Blackwell 化をしたいのか?
Rao-Blackwell 化の話の前に,amcl の枠組みに対して特に工夫をすることなくSLAM を導入したらどういうことになるか考察してみます.
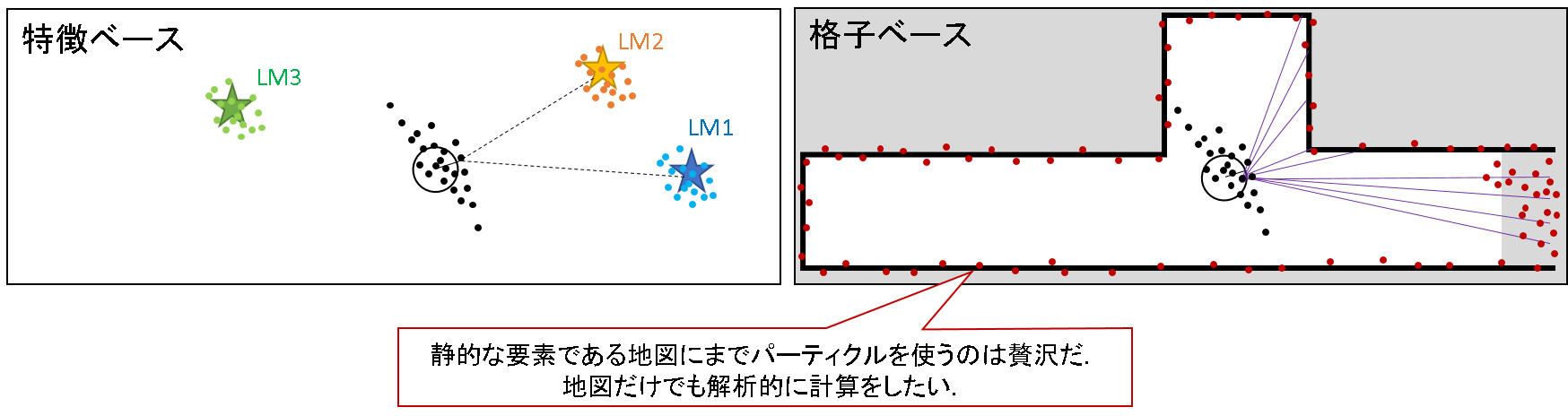
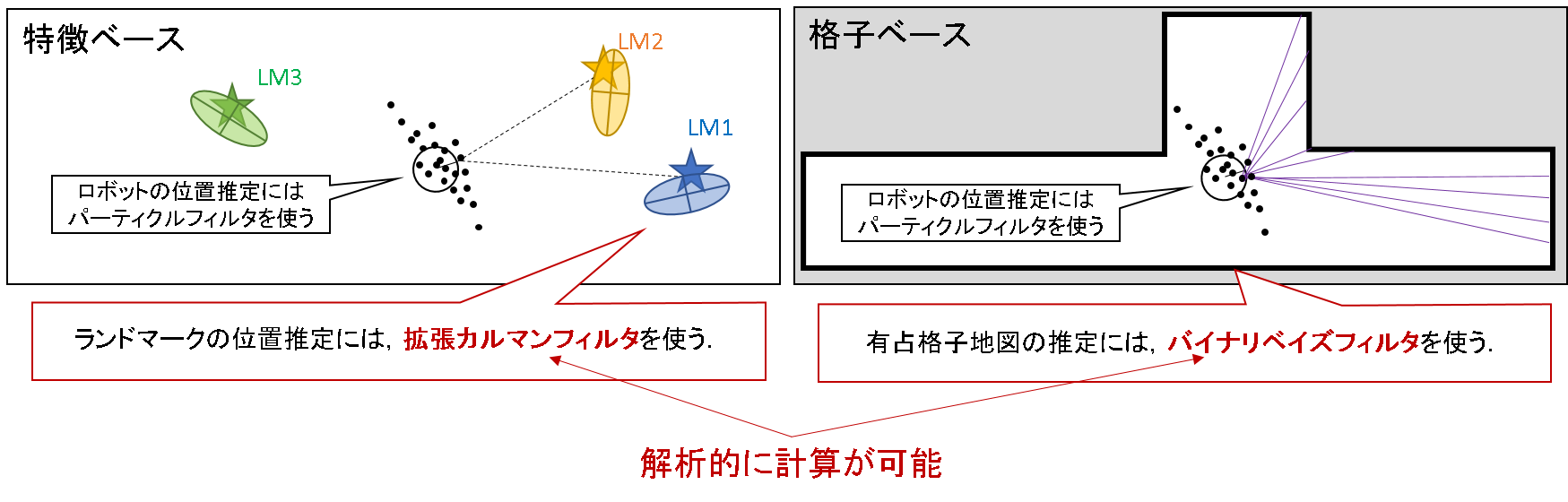
ロボットの位置だけではなく地図もパーティクルで推定しようとしたらどうなるでしょうか?例えば,下記のようなイメージになるでしょう.
特徴ベースであればランドマークの位置を,格子ベースであれば壁の位置をパーティクルを使って推定するようなイメージです.どう思いますか?随分無駄なことをしているように見えませんか.
なぜなら,特徴ベースであろうが,格子ベースであろうが,推定対象の地図は「静的」であるはずです.地図のような不動の対象に対してまで多数の粒子によるモンテカルロ近似を行うとなると,もはやいくつ粒子を用意すればよいのか分かったものではありませんので,計算量が膨大となります.
そんなリソースがあるくらいなら,時々刻々と変動するロボットの位置推定に割きたいものです.ですから,ロボットの位置推定はともかくとして,地図だけでももっと簡単に求めることはできないだろうか?という発想が生まれるわけです.
より具体的には,特徴ベースではランドマークを「拡張カルマンフィルタ」で,格子ベースでは壁を「バイナリベイズフィルタ」によって求めています.gmapping では後者を採用しており,これも後ほど触れることに致します.
Rao-Blackwell 化の定式化とイラストによるイメージ
そこで,Rao-Blackwell 化の登場です.推定したい状態量の中に「パーティクルで近似して求めるもの」と「解析的に求めるもの」が含まれる場合,それらを分割する処理を行います.最もシンプルなRao-Blackwell 化の数式を見てみます.
ただの条件付き確率です.これにより,パーティクルで表現する「ロボットの軌跡」と,解析的に計算をする「地図」を求める式を分割することができました.ただし,「地図」は「ロボットの軌跡」に従属する形をとります.だから,「事前推定」をしたとに,「地図の更新」をするのですね.軌跡が全時刻のものになっていることは後述の「完全SLAM問題」の節で,解析的な地図の計算方法についてはこれも後述の「有占格子地図」で説明します.
これをSLAM 問題で扱うパラメータを用いた形へと展開させます.観測zで,入力uを条件とした式となっています.
Fast SLAM に至るには,もう一段階必要です.ロボットの軌跡も地図も各パーティクルに紐づくのです.右上付きかぎ括弧でパーティクルのインデックスをkを添えて,「パーティクルkに関する推定値」という意味を持たせます.
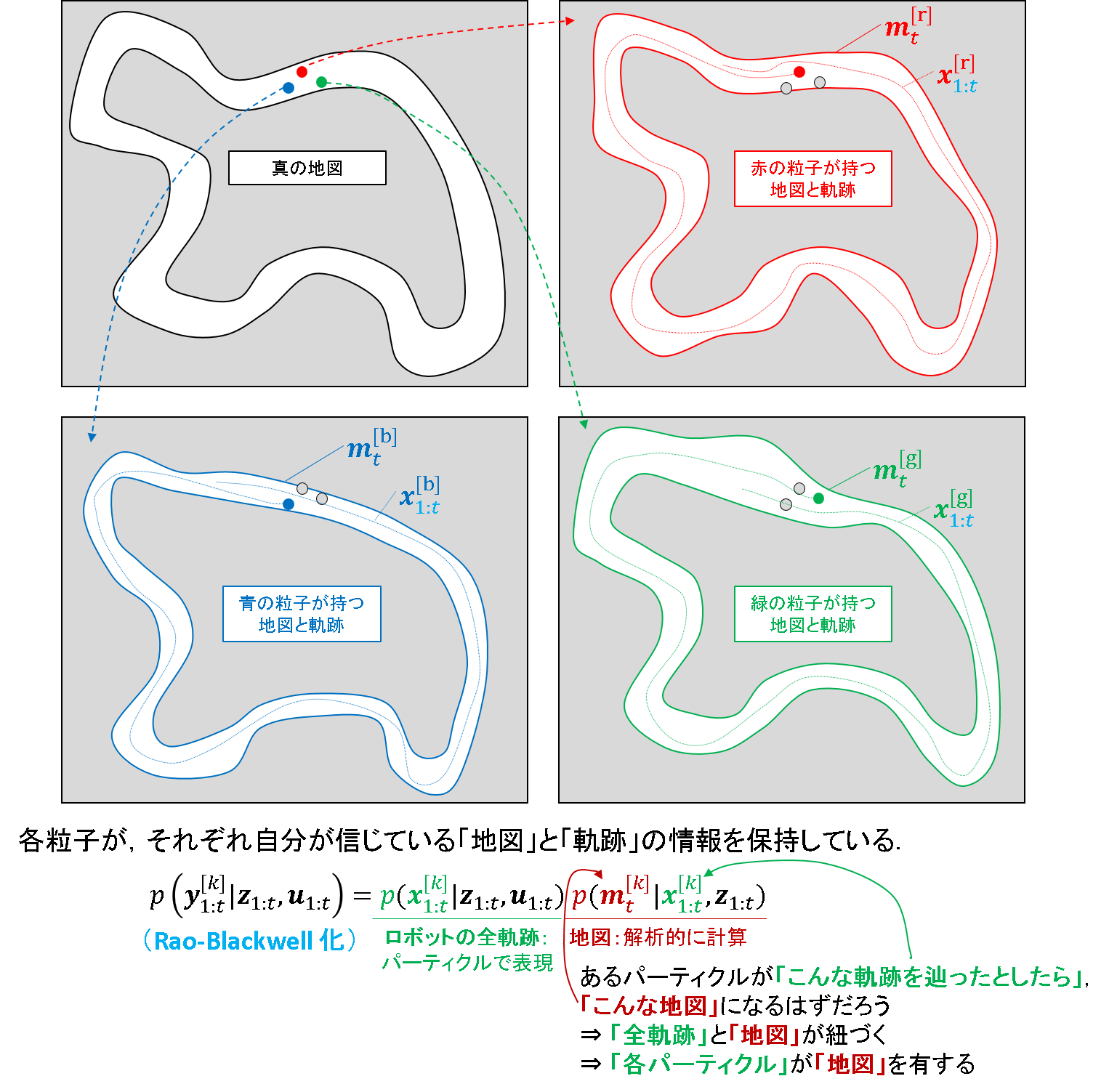
これを具体的にイメージすると,下図のようになります.
神のみぞ知るある真の地図を推定するために,3つのパーティクル(赤,青,緑)を使っているものとします.このとき,各パーティクルがそれぞれ独立に自身の通過軌跡と地図を持っているというものです.
今一度,地図を算出する条件付き確率の式を眺めてみます.パーティクルkの過去の軌跡全てを総動員した結果,kに紐づく地図が推定されるという式です.これは,パーティクル1つに対して地図が1つ割付くことに他なりません.ここまでイメージできるようになると,RaoBlackwell 化というのもシンプルな話なのだと理解できそうです.
前回まで考えてきたパーティクルフィルタとの違い
「RaoBlackwell 化いいですね,便利になりましたね」と流してもいいところなのですが,何かひっかかるのです.はやる気持ちを抑え,少し寄り道的に考察をさせて頂きたく.ご容赦願います.
さて,これまでパーティクルフィルタで状態推定をするといったら,こんなイメージでした.
- 求めたい状態が取りそうな「分布」を,多数の粒子によって近似する.
そうです,パーティクルフィルタは元来「分布」を近似するための仕組みを提供していました.ところがここにきて,仮定がガラッと変わります.
- 各パーティクルは,自分が過去に通過した「位置の軌跡」と「地図」を有する.これらは「状態推定値」そのものであるので,「分布」を近似するための機構にはなっていない.
- 例えば,各パーティクルが持つ「状態値の軌跡」や「地図」の重み付き平均を取ることと,ベイズフィルタで事後分布を求めることとの関係性を導くことができない.
- ただし,現在位置のみだけは「分布」を形成する.これはベイズフィルタによる更新が有効である.
- ここだけは,従来のパーティクルフィルタと同等の仕様を実現できる.
こいつ何を言っているんだと思われてしまうかもしれませんが,これは私にとっては大きなパラダイムシフトです.
だって,動作モデルによって「事前分布」を粒子で近似して,これを尤度モデルによって「観測更新」する.これによって「事後分布」に相当する中間的な荒い分布を導出しておいて,アプリケーションに適合させたうまい方法で「事後推定値」を算出する,っていうのがオリジナルのパーティクルフィルタのコンセプトだったはずです.
ごちゃごちゃ書いてしまって恐縮ですが,つまり最終的に算出したい「事後推定値」を求めるときに,「粒子の集合が持つ情報群」を連携させるというのが,ベイズフィルタ的にはしっくりとくる解釈だと思うのです.
このコンセプトをイラストで解釈したものを,下記の記事で説明しました.
一方,RaoBlackwell 化した粒子が持つ「軌跡」と「地図」に関しては,他の粒子の持つ情報を連携させて,例えば「重み付き平均」を導出することに,理論的な意味付けができそうにありません.
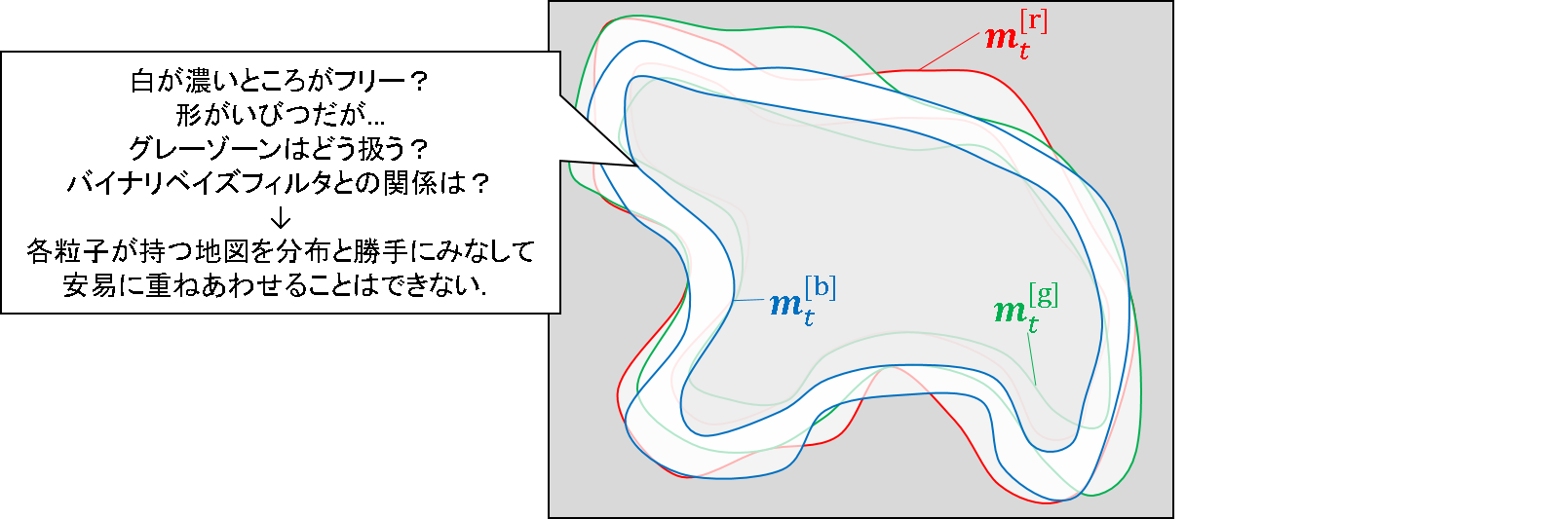
より具体的には,上述した地図の図の中に出てくる3つのパーティクル(赤,青,緑)が持つ地図を画像とみなして平均したところで,本当に求めたい地図を再現できそうな雰囲気は全くありません.各パーティクルが勝手に動きまわってかき集めた情報を元に作った地図です.
例えば,各粒子の持つ地図を無理やり分布と考えて,下手に重み平均をとった所でメチャメチャな値になることは思考実験上も明らかです.何かうまい方法が見つかる可能性は否定できませんが,バイナリベイズフィルタとの関係はきちんと議論しないと難しいでしょう.
そういう背景もあるからでしょうか?結局RaoBlackwell 化した場合の最終的な事後推定値は,「最大重み推定」を行っているようです.少なくとも,gmappingではそうです.これについて,もう少し解釈をしてみます.
まず,RaoBlackwell 化をしていないパーティクルフィルタの枠組みで「重み付き平均」による事後推定を行ったとします.その場合,「そこそこの尤度を持つ粒子」も「事後推定」の結果に影響をあたえることができました.いわば団体戦の様相を呈しています.
しかし,RaoBlackwell 化した推定の場合には,「勝者総取り」です.最も尤度の高い粒子が有する「現在位置」,「過去の軌跡」,「地図」をまるごと現時刻の事後推定値としてしまう.RaoBlackwell 化の構造上,そういう仕様によって推定することは確かに妥当だと思います.
このイメージを下図に示します.
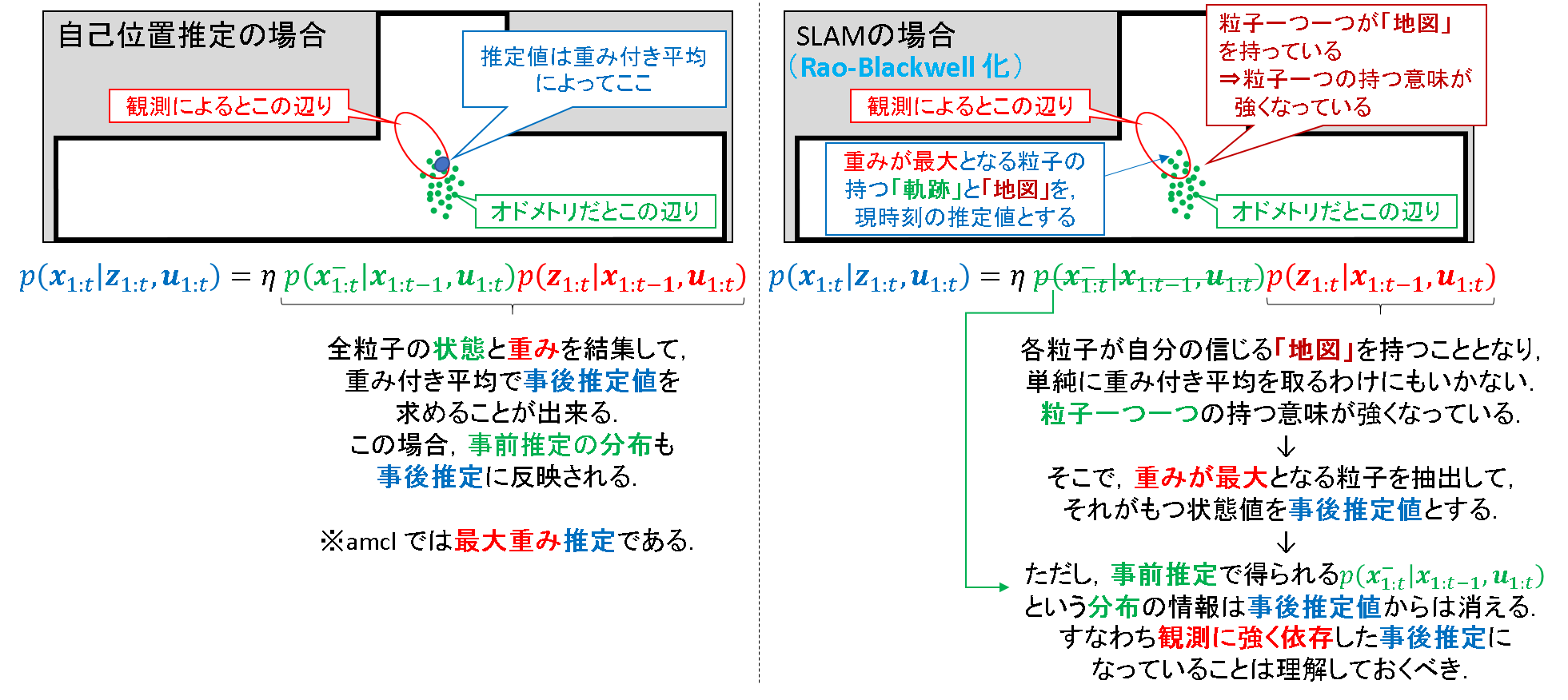
※一応補足をしておくと,RaoBlackwell 化をしていないパーティクルフィルタでも「最大重み推定」は可能です.事実,amclはそうです.ただし,後述するような理由でベイズフィルタ理論的な根拠は,「重み付き平均」の場合よりも薄まってしまう点は理解しておく必要があります.
ただし,「最大重み推定」は注意が必要です.「事後推定値」算出に際し,粒子で近似した「事前分布」の情報はかき消されてしまいます.だったら最初っからオドメトリなんて面倒なことをしないで観測情報だけで推定してしまえばいいという議論も出てきそうです(この発想は,オドメトリフリーのHector SLAM へと展開されていきます).
それでも,パーティクルフィルタにはもう一つ強力な特長がありました.ランダムパーティクルを混入させることで,誘拐問題に対処できるという点です.それに,「最大重み推定」は計算コスト的にも優位性があります.だから,多少理論的な厳密性には目をつむって「最大重み」をつかってでも,外乱に対して頑強なパーティクルフィルタが愛されるのだと理解できます.
この辺りの特性はパーティクルフィルタの本質に関わる部分ですし,後述するFast SLAM 1.0 からFast SLAM 2.0 へ展開する際にも非常に密接に関わる特性と言えるので,敢えて何度も書いていくこととします.もう少し詳しい話は,やはり下記記事で説明しています.
とにかく,Rao-Blackwell 化されたパーティクルフィルタを使う上では,注意が必要だということを,頭の片隅には入れておく必要がありそうです.
おわりに
ああ,文字ばかりで,ごちゃごちゃしてしまいました^^;
でも,実はここで議論したこと,次節の「オンラインSLAM問題」と,「完全SLAM問題」を解釈する上でも非常に重要な論点だと思うのです.ということで,というわけで,次回の「オンラインSLAM問題と完全SLAM問題」において,ここでの議論の一部を引っ張り出してながら,これらの対応点についても触れようと思います.
- 応用編
- Fast SLAM 1.0
- Fast SLAM 2.0
- Fast SLAM 1.0 とのイラストによる比較
- Fast SLAM 1.0 との数式による比較(ランドマークベース)
- ランドマークベースから格子ベースへ
- 準備編 その1
- Fast SLAM の基本フロー
- Rao-Blackwell 化
- 準備編 その2 ← つぎココ
- オンラインSLAMと完全SLAM
- 有占格子地図
それでは.
Next:
Prev: 3.3 原理をみる (応用編)
参考文献
- ROS Wiki.
- S Thrun, et al., "Probabilistic Robotics", the MIT Press, 2005.
- Grisetti, Giorgio, Cyrill Stachniss, and Wolfram Burgard. "Improved techniques for grid mapping with rao-blackwellized particle filters." IEEE transactions on Robotics 23.1 (2007): 34-46.
- "ros-perception/slam_gmapping", github.
- なぜパーティクルフィルタの推定値に「重み付き平均」が使われるのかを考察してみた