目次
- 導入
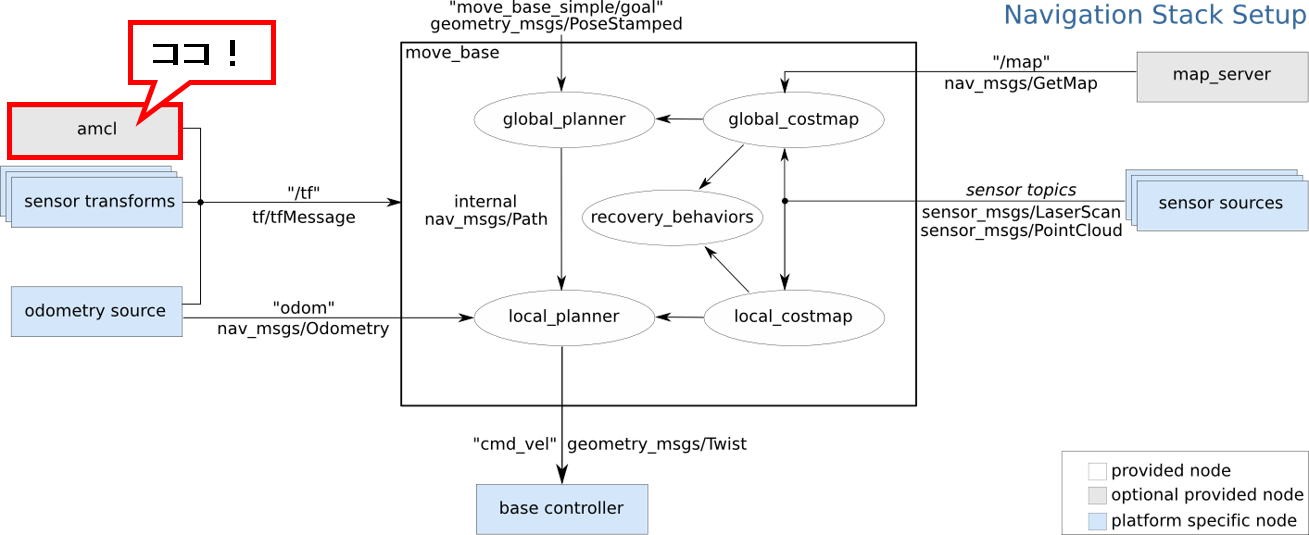
- move_base (ナビゲーション)
- ROSで遊んでみる
- ソフトウェア構成をみる
- amcl (自己位置推定)
- ROSで遊んでみる
- ソフトウェア構成をみる
- 原理をみる (準備編)
- 原理をみる (応用編) ← いまココ
- gmapping (地図生成)
- ROSで遊んでみる
- ソフトウェア構成をみる
- 原理をみる(応用編)
- 原理をみる(準備編 その1)
- 原理をみる(準備編 その2)
はじめに
Navigation Stack を理解する - 3.3 amcl: 原理をみる (準備編)の続きです.前回は,パーティクルフィルタを使って自己位置推定を行うことのメリットを理解していきました.この理解を前提に,実際にProbabilistic Roboticsで紹介されており,かつROSのamclパッケージで実装されている自己位置推定法の理解を深めていきます.
流れ
amcl は,一般的なパーティクルフィルタのアルゴリズム+自己位置推定に特化した技巧的な処理,という構成であると解釈すると分かりやすいと思います.なので,説明のフローは下記の通りとします.
- 自己位置推定の基本フロー(パーティクルフィルタの一般的なフロー)
- オドメトリによる事前推定
- 観測に基づく尤度の計算
- 推定値の算出
- amcl の技巧的処理
- 尤度モデル
- 定常的なノイズ成分
- 障害物対策のノイズ成分
- 乱反射対策のノイズ成分
- 誘拐対策のノイズ成分
- サンプリング
- Augmented MCL
- KLD Sampling
前半は,パーティクルフィルタの一般的なフローのお話をします.あまり面白くないかもしれませんが,ここを理解しないと以後の技巧的処理の必要性を理解できません.
後半は,amclの技巧的な処理を,尤度モデルとサンプリングの節に分けて説明します.それらの処理の必要性やメリットは,適宜本文の中で盛り込むようにしました.
これらの項目はあくまで「最も主要な」要素に過ぎず,ここに記載したもの以外にも種々のtipsは埋め込まれているはずです.そういう詳細な部分については記述は今回はしておりません.さらなる詳細を知りたい方は,適宜Probabilistic Roboticsや,amclのコードを参照ください.
前提条件
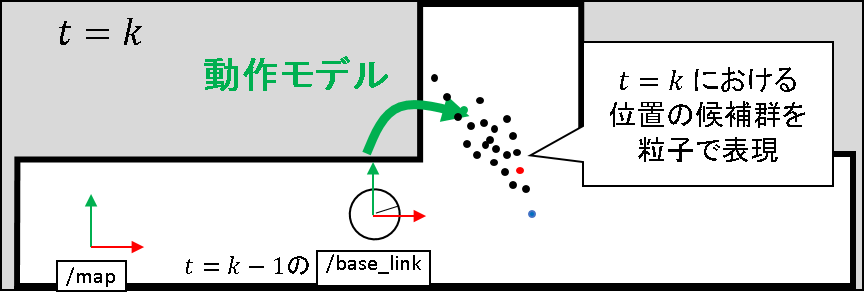
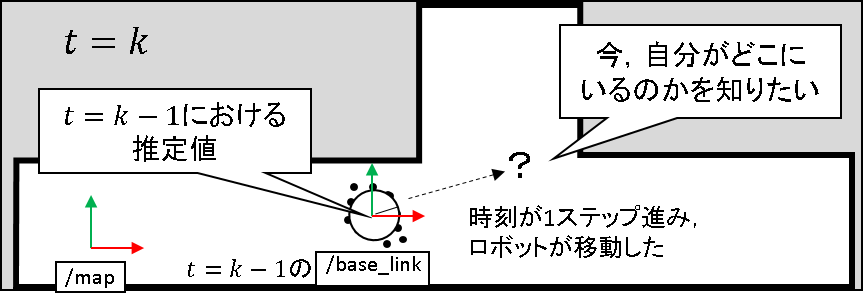
時刻 t = k-1 で,自己位置推定もリサンプリングも終わっているものとします.下図のような状態で,おおよそ粒子はロボットの推定位置である /base_link フレームの辺りに撒かれているものとします.

さらに,地図は事前に作成されているものを利用しているものとします.
今,時刻 t = k になったとします.今,自分がどこにあるのかを知りたい.この段階です.
自己位置推定の基本フロー
オドメトリによる事前推定
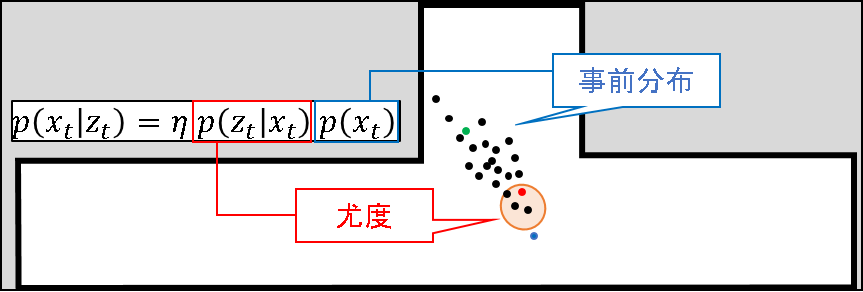
まず,オドメトリによる事前推定を行います.下記ベイズフィルタの,緑色の確率分布に相当します.
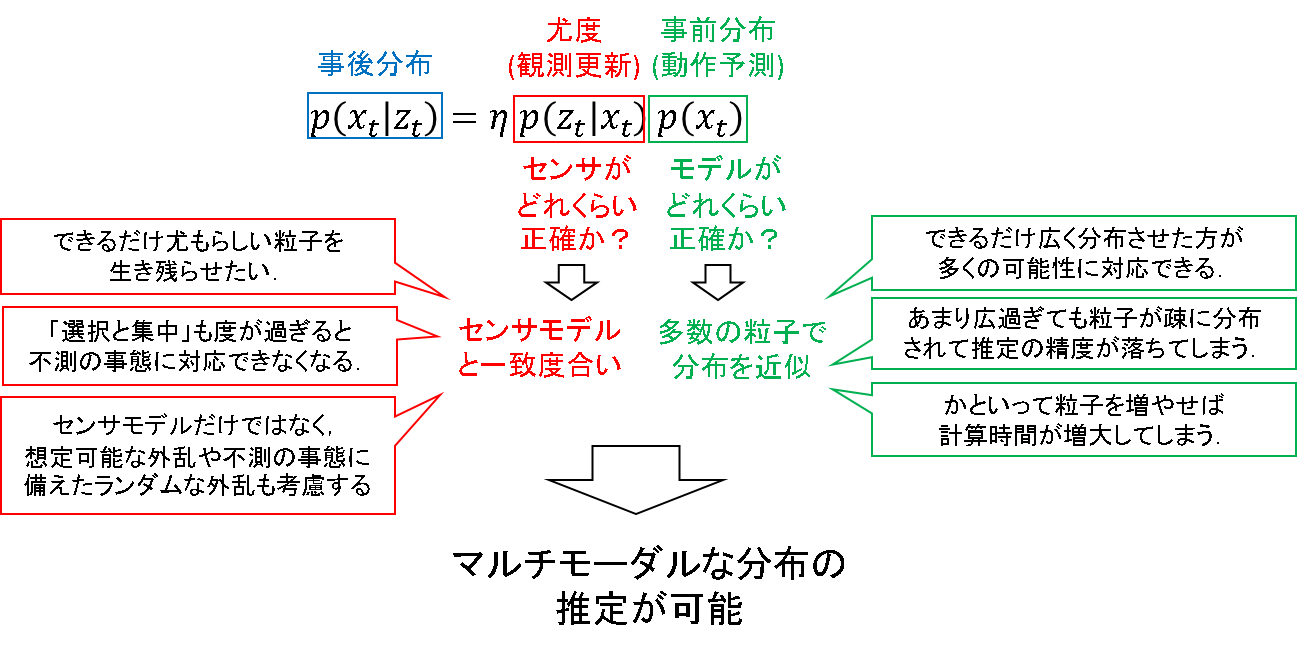
動作モデルに従って,粒子をばら撒きます.任意のノイズを仮定して,もとあった領域よりも広い領域に粒子をばら撒いていきます.各粒子は,「モデルを信じるならロボットの位置はここにあるかもしれないよ」という状態値の仮説を表しています.
こうしてばら撒かれた粒子のうち,どの粒子が「尤もらしい」のかを,観測情報を照らし合わせながら評価していきます.その結果をもって,t = k における推定値を算出していくことになります.
観測に基づく尤度の計算
広い領域にばらまかれた粒子のうち,どの粒子が「尤もらしい」のかを計算しましょう.さて,どうやってそんな評価を行うのでしょう?
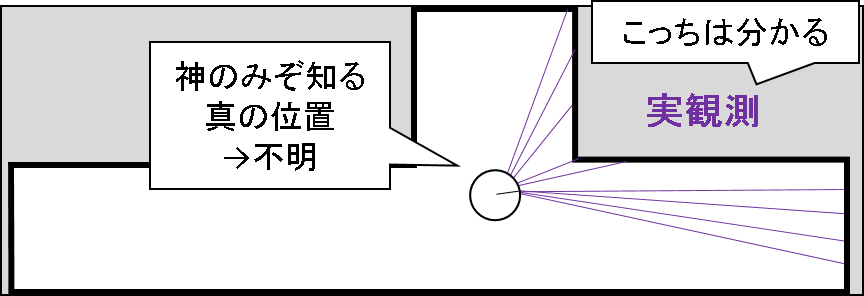
まず今持っている情報を整理してみましょう.当然,観測情報を持っています.LRFから得られたレーザ長の集合を持っています.ロボット自身は神のみぞ知るある位置に存在しているのですが,そこにセンサをおいたら実際にはこんな値が得られたぞ,という情報を持っています.
次に,各粒子は自分の状態値(ここでは,ロボットの位置と姿勢)を持っています.さらに,地図の情報を持っていることも前提となっています.するとどうでしょう.地図上のある位置・姿勢でセンサを配置したら,こんな値が得られそうだ,というモデルを立てるのはそんなに難しい話ではなさそうです.
下図のように,ばら撒いた粒子群からセンサ値が異なる3つの粒子を抜粋して,その予測観測値をイメージしてみましょう.!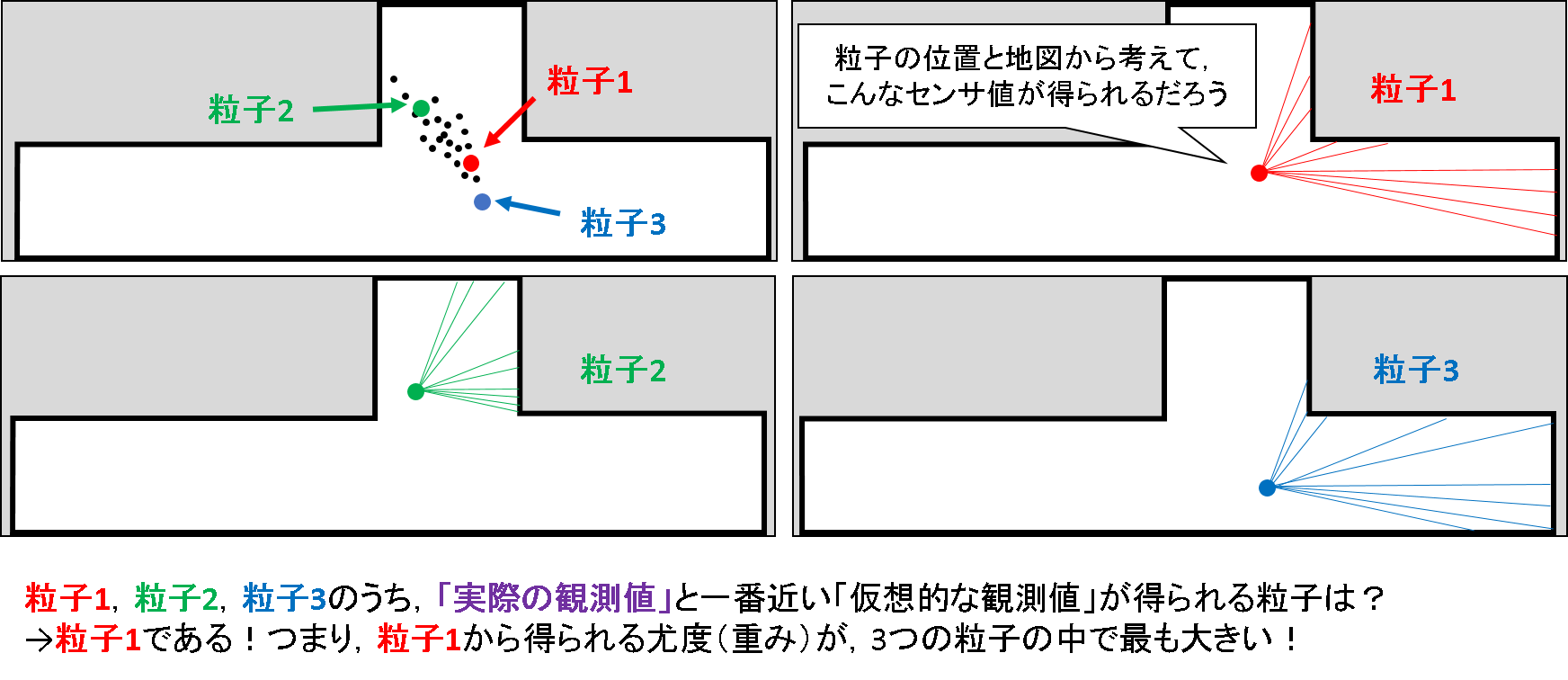
このうち,前述した「実際の観測」と最も近いレーザの分布を持つ粒子はどれでしょうか?目視で確認できると思います.そうです,粒子1です.すなわち,上記3つの粒子のうち,観測と照らし合わせた時に,最も尤もらしい状態値をもっていると言えそうです.この尤もらしさのことを「尤度」と呼びます.解析的なり数値的なりにでも,最も大きい尤度をもつ状態を推定できる場合は,その推定自体を「最尤推定」と呼んだりします.
ただし,尤度の大きさは観測への依存が強くなる傾向があります.せっかく事前推定によって広い範囲に粒子をばら撒いたのに,最尤推定を行うことで事前推定で得られた可能性を切り捨ててしまう可能性を否定することはできません.パーティクルフィルタを使う上では,そこは理解しておく必要があるでしょう.
ただ,この尤度のイメージはちょっと配慮が足りません.amcl ではもっと賢い尤度モデルを利用しているのです.それは後述することとして,一旦推定値の算出まで終わらせてしまいます.
推定値の算出
amcl では,ばら撒かれた粒子の中から重みが最大となるものがもつ状態値が推定値として算出されます.
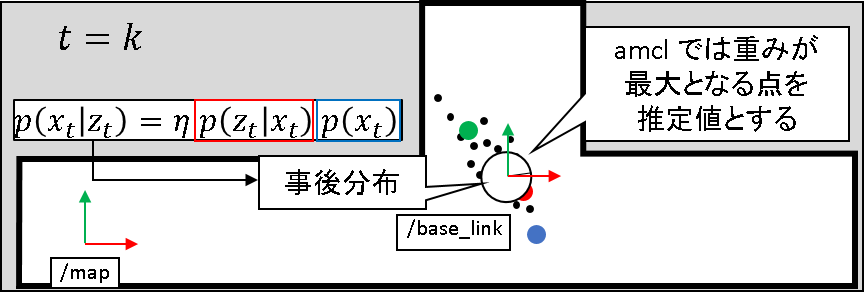
これが妥当なのか?という話は,下記記事に譲ることとします.結論としては,オドメトリは不正確だけど,センサがそこそこ正確であれば,この仮定も悪いものではない,と解釈できます.
ここまでが基本の基本です.通常のパーティクルフィルタの範疇の話であり,あまり面白いものではないかもしれません.ここからが,amcl における技巧的な処理のお話となります.
amcl の技巧的処理
amcl で工夫している点は,大きく分けて「尤度モデル」の置き方と,「粒子の分布」です.それぞれ,観測モデルと事前推定モデルを改善していることになります.ベイズフィルタの理論に基づけば,これらのモデルが正確であれば,事後推定も正確に求まることになっています.したがって,これらのモデルに改善のメスを入れるという発想は,当然と言えば当然です.
ただそれを自分で思いつくかというとまた別の話です.実によくできていると思います.私の解釈している範囲でイラスト用いて説明をしていきます.
尤度モデル
これまで散々布石を置いてきた,尤度モデルです.ようやく出てきました.
amcl で扱う尤度モデルは,「定常的な観測ノイズ」に加えて,「想定できるノイズ」や「ランダムなノイズ」を混入させるようなモデルとなっています.まずは,定常的なノイズから説明をはじめます.それだけだと問題が生じるから,色々なノイズを混ぜるといいんだよ,という手順で話を進めていくことにします.
定常的なノイズ成分
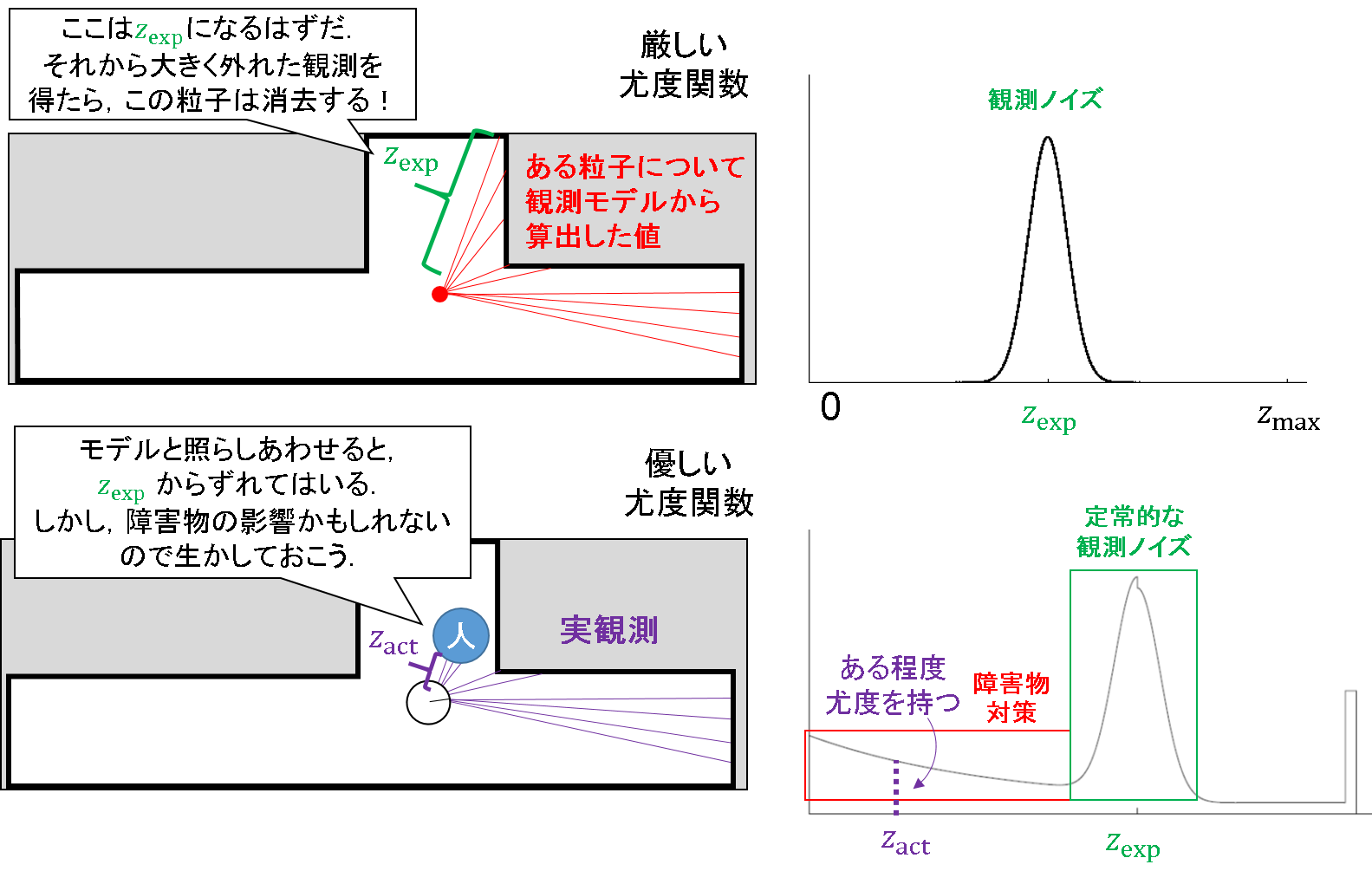
センサ値を中心としたガウス分布を想定しています.他に特殊な外乱がない環境であれば,悪い仮定ではありません.
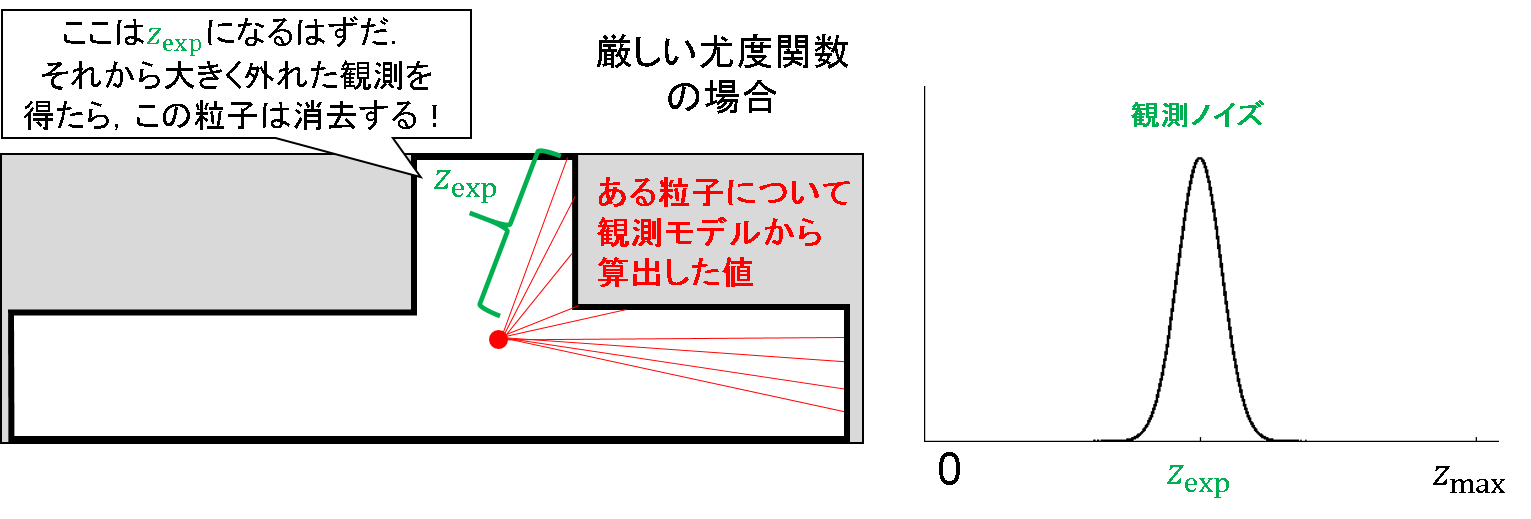
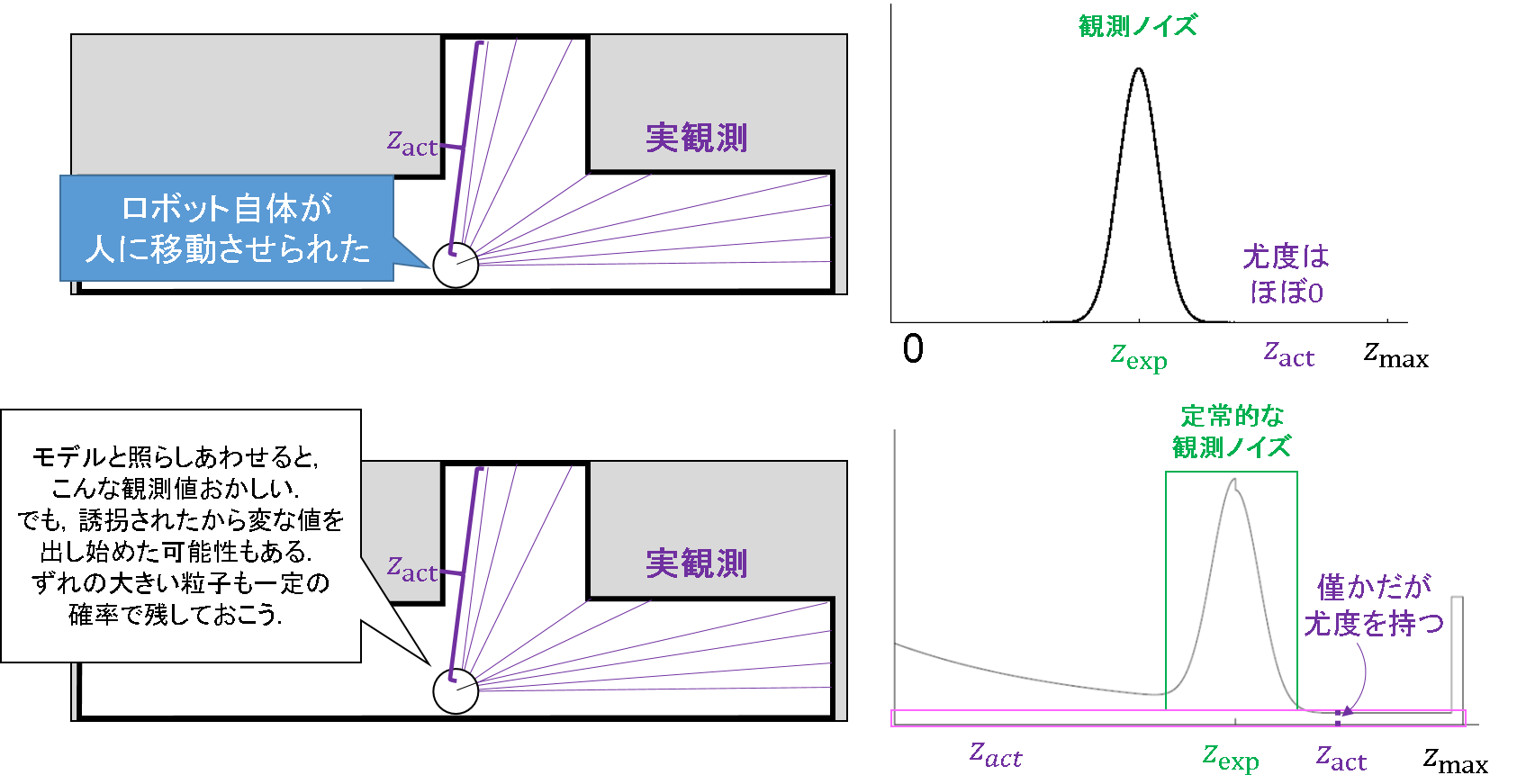
ただ,厳しい仮定ではあります.ガウス分布に従わない値が得られる場合,「そんなものはあり得ない!」と一蹴してしまう危険性があります.例えば,たまたまある時刻で人がロボットの前に表れたとします.すると,地図と理想的な観測モデルから得られるであろう値(z_exp)よりも,だいぶ小さいセンサ値(z_act)を得ることとなります.
さぁ大変です.そんな嘘っぱちの情報を吐く粒子は消してしまおう!だって,ガウス分布に従っていないんだから!という展開になってしまいます.当然,尤度の値は小さくなるわけですから.
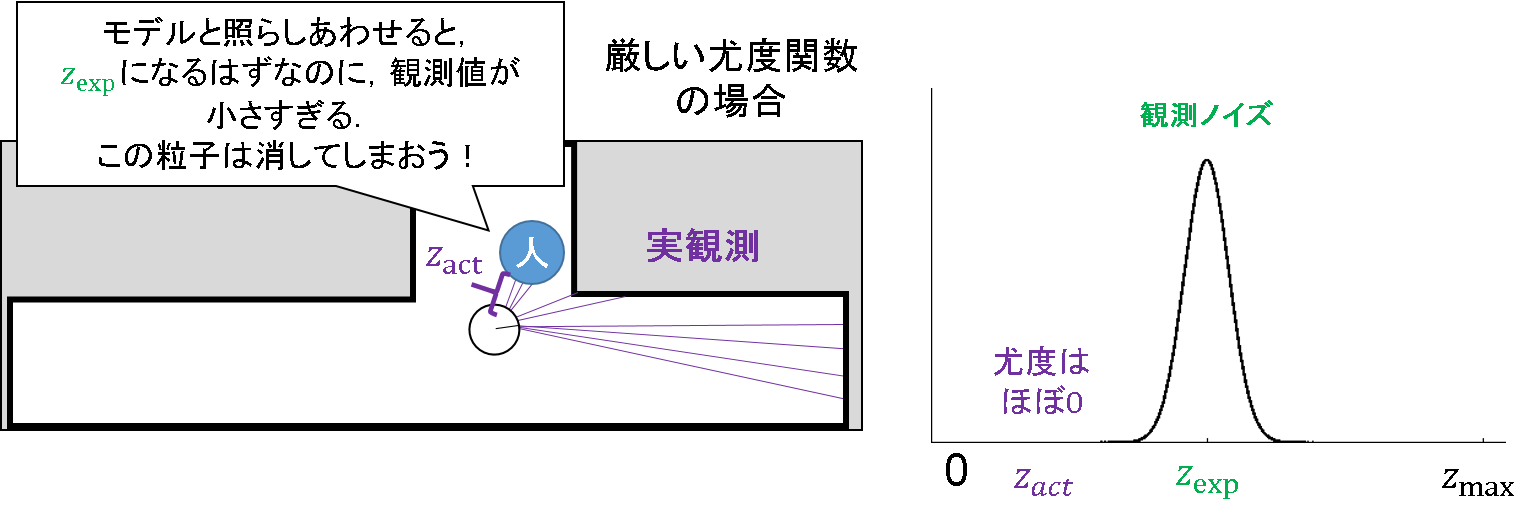
せっかくパーティクルフィルタを使って多様的な状態値の仮定をおけるのに,みすみすその特長を捨ててしまうのはいかがなものか?というお話です.そこで,以下のような混合ノイズ分布を考えよう,という流れになるのです.
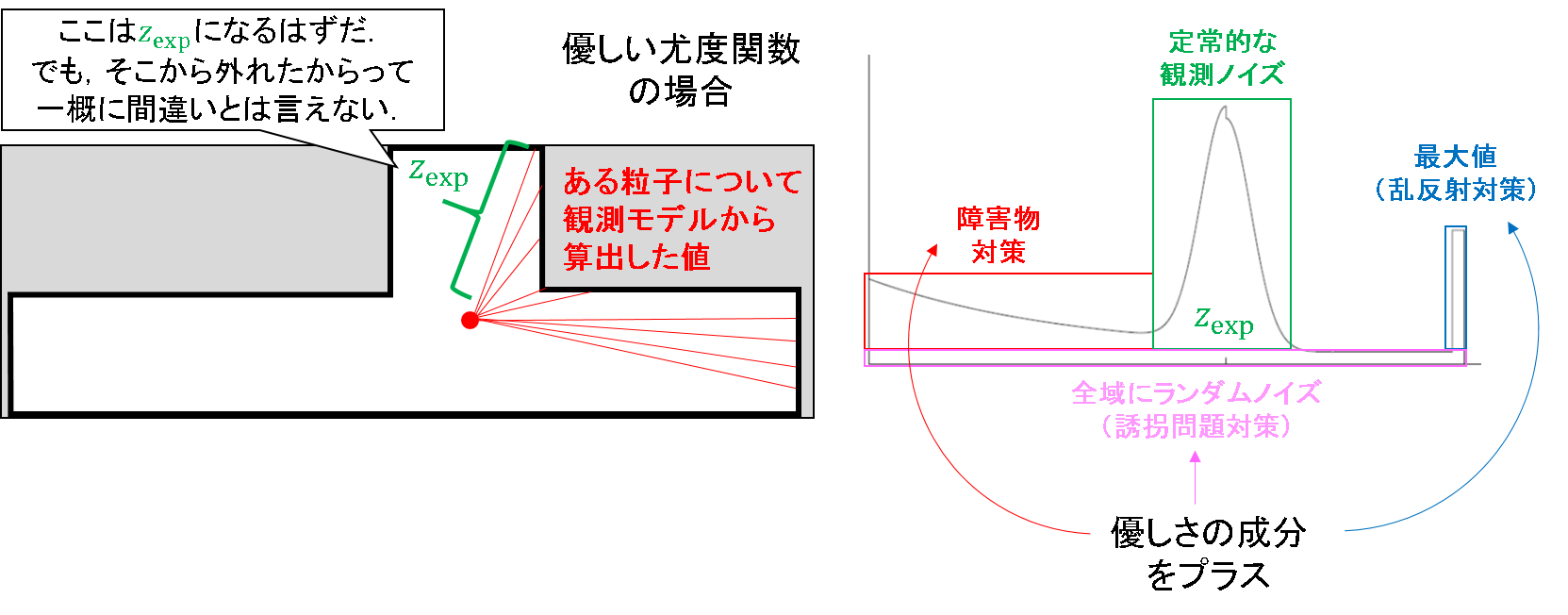
ガウス分布に多少従わなくても,ある程度尤度を与えてあげましょうよ,という「優しさ(?)」の成分が混入されたノイズモデルとなっています.具体的には,「障害物対策のノイズ成分」,「乱反射対策のノイズ成分」,「誘拐対策のノイズ成分」に分けられます.これら一つ一つについて,ケーススタディをしてみます.
障害物対策のノイズ成分
先程説明した,「ガウス分布に従わない観測値を吐く粒子を消してしまおう!」というスタンスの厳しい観測ノイズモデルと照らし合わせた図を見てみましょう.
改善版の観測ノイズモデルの場合,期待観測値(z_exp)よりも左側にある程度尤度を持たせるような仕様になっています.この場合,確かに観測値からはずれてしまったとしても,人や障害物がいたらモデルによって得られる期待観測値(z_exp)よりも,実観測(z_act)の方が小さくなることなんてあり得る話だということを,陽に考慮しているのです.これにより,多少の障害物でもへこたれない状態推定が可能となります.
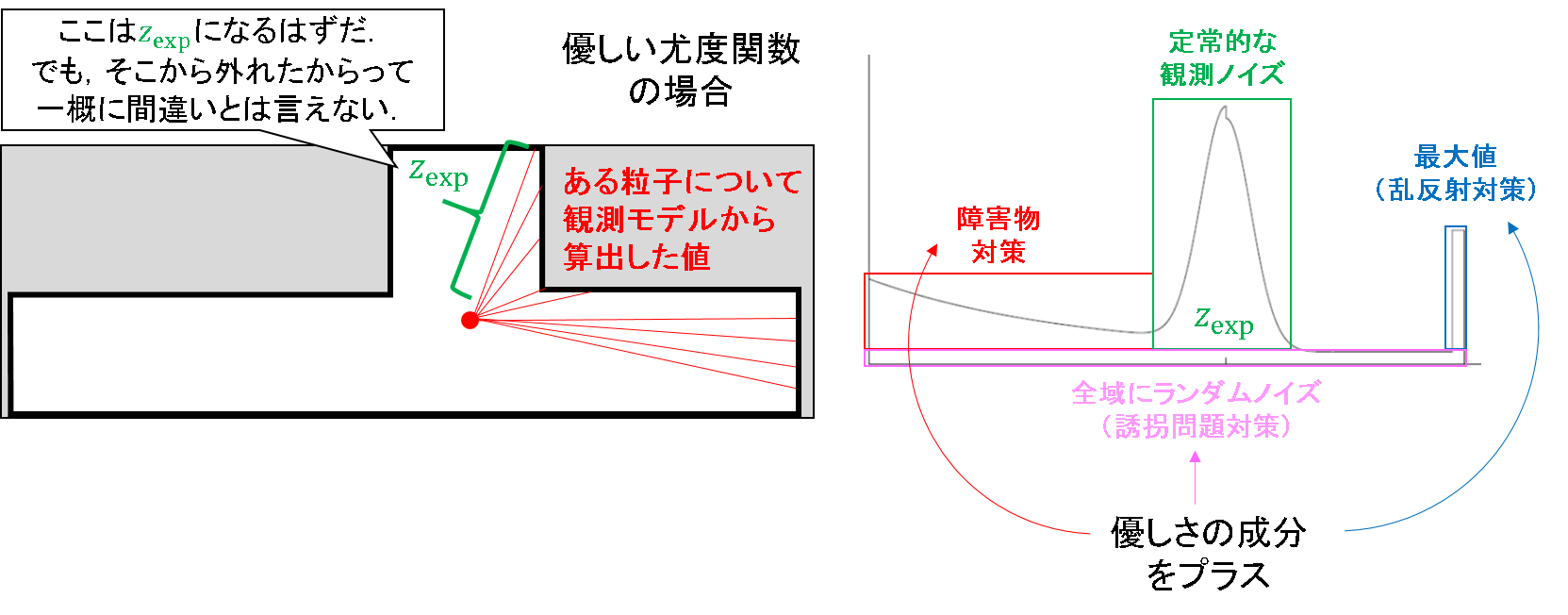
乱反射対策のノイズ成分
今度は,障害物とは反対です.得られる観測値(z_act)が,期待観測値(z_exp)よりもずーっと大きい,最大値を吐き出してしまうことがあるのです.これは,レーザーが当たった場所で変な方向に反射してしまって,正しい距離情報を得られない場合を考慮してのことです.そんな場合にも,障害物で説明した場合と同じように,粒子が理不尽に社会不適合者の烙印を押されてしまうことがあるのです.粒子は悪くないのに,です.
そこで,センサの得る距離値の最大値の辺りにも尤度を持たせるようなノイズを混入させておこうという発想です.
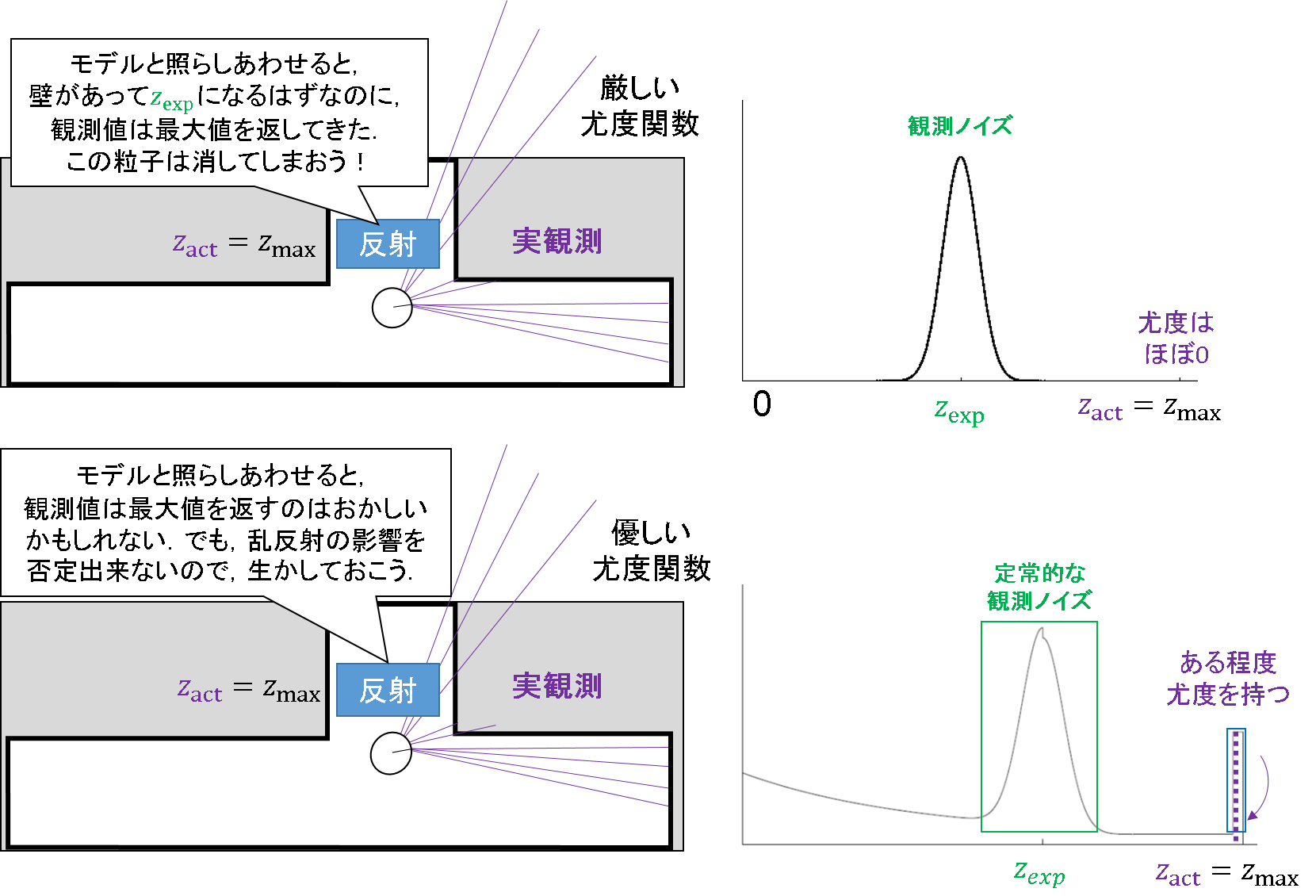
これにより,乱反射でたまたま実センサ値と適合しない粒子を保存できる仕様が追加されます.
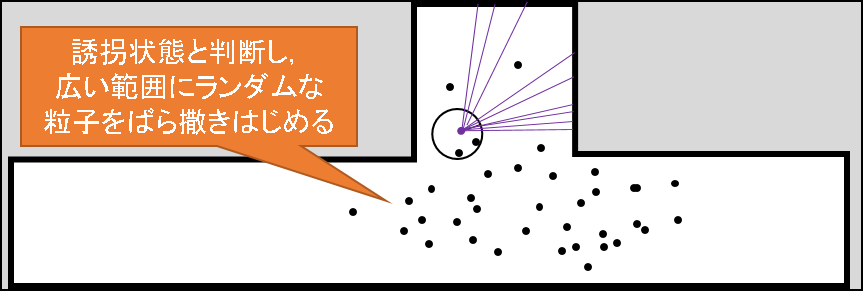
誘拐対策のノイズ成分
「障害物」や「乱反射」は比較的予想しやすく,モデルを立てるのもそんなに難しくはありません.しかし,予想がしにくい不測の事態もあります.それが,「誘拐」です.
これは最悪です.突然だれかがロボットをひょいを持ち上げて別の場所まで運んでしまうのです.これまで想定したガウス性ノイズの仮定が完全に崩壊するのはもちろんのこと,「障害物」や「乱反射」のノイズでも対応可能範囲には限界があります.どこに連れていかれるかなんて,前に行くのかも後ろに行くのかも,まったくもって知ったこっちゃないわけですから.
そんな不測の事態に対応するために,観測範囲全域に一定のノイズを仮定します.もう誘拐となったら何も分からないんだから,適当に広い範囲に粒子を撒いてしまえというわけです.
ノイズのまとめ
もうノイズはお腹いっぱいですね笑.いったんまとめましょう.
- 定常的なノイズ成分
- ガウス性ノイズ.あくまで理想的な状態しか想定できず,環境変化には弱い.
- 障害物対策のノイズ成分
- 期待観測値よりも近い値が出た場合でも,障害物の可能性を考慮して粒子を生き残らせる.
- 乱反射対策のノイズ成分
- 最大値を返す場合は乱反射の影響かもしれないので,その場合も粒子を生き残らせる.
- 誘拐対策のノイズ成分
- もはやどこに飛んでいくのか分からないので,観測可能な全域に渡って一定尤度を与える.
こういうノイズ成分を混合させることで,粒子の多様性を生かした状態推定ができるのですね.
さて,ここまで観測の情報をもとにどう粒子を生き残らせるかを議論してきました.尤度の計算方法を工夫してきたわけです.
これ以降は,どう粒子をばら撒くかを議論していきます.事前推定のサンプリングに影響する部分です.とても興味深い手法ですので,引き続き紐解いていきましょう.
サンプリング
粒子のサンプリングも悩みの種です.正確に分布を近似したり,不測の事態に備えようと思うなら,大量の粒子を広範囲にばら撒き続ければよいということは,直観的にも当然の帰着となります.
しかし,あまり粒子数を増やすと計算量が大きくなりますし,広すぎる範囲を仮定してばら撒き続けると,無駄な粒子を常に追い続けなければなりません.ここでもバランスが重要になってくるのですが,そのバランスのとり方を動的に切り替える方法もamcl で実装されているのです.ここでは,そのバランスのとり方について見て行きます.
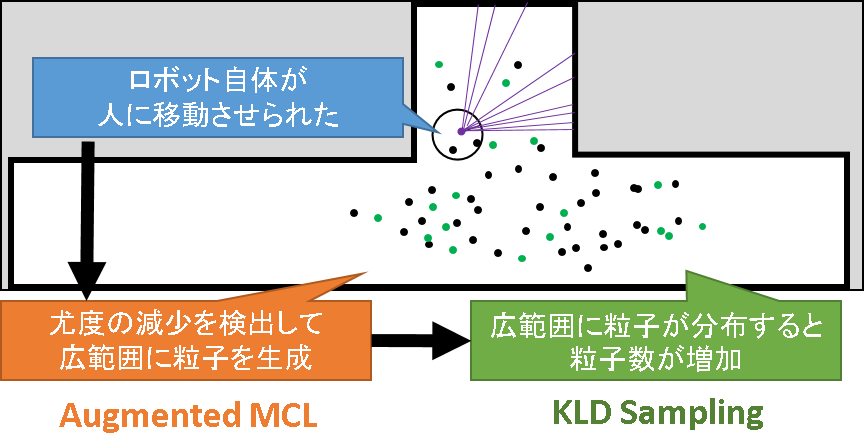
例えば,誘拐問題に対応するために,多数の粒子を広範囲にばら撒き続けるようなノイズを仮定したとします.すると,そんなことをする必要がない比較的安定した推定ができる状態においても,たくさんの粒子について計算をし続けなければなりません.かといって,そんな安定状態に合わせて粒子を少なくしてしまうと,いざ誘拐されたときに対応することができません.ではどうするのか?というのがここでの問題です.
結論を言うと,安定状態と誘拐状態を見極めて粒子をばら撒く範囲を動的に調整したり,粒子の数を動的に増減させたりするようなサンプリングを行うことでこの問題を解決します.前者の処理を「Augmented MCL」, 後者の処理を「KLD Sampling」と呼びます.それらは相互に連携することで,相乗効果を生むような仕様になっています.
Augmented MCL
ここでは,位置推定が順調に行われている「安定状態」と,突然どこかに飛ばされてしまった「誘拐状態」を見極め,粒子のばら撒く範囲を調整します.
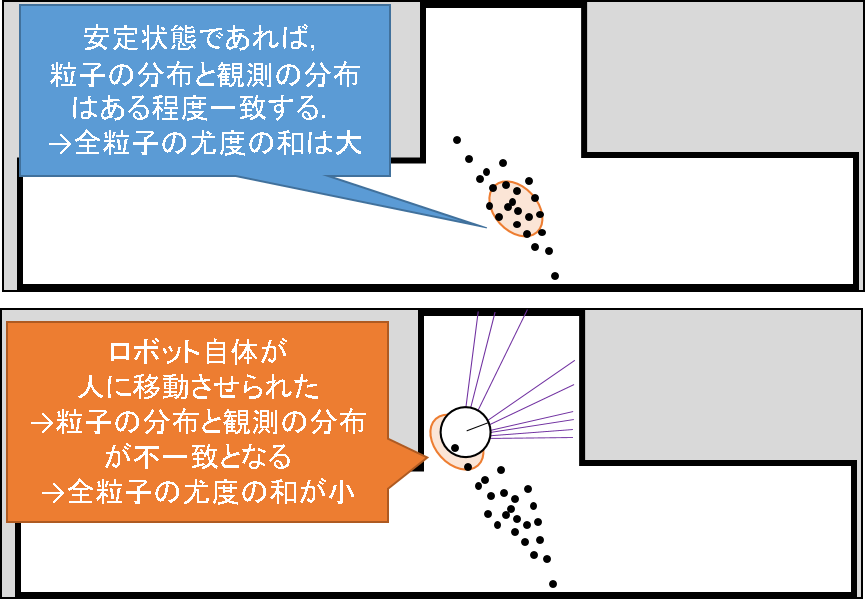
ミソは,「安定状態」と「誘拐状態」の見極めです.この鍵となるのが,尤度の計算です.次の図を見てみましょう.
推定が安定している場合は,粒子が集中している個所と,観測尤度の中心がそんなに大きくはずれません.もちろんある程度はずれるでしょうが,次で見る誘拐状態に比べればましな状況であることには変わりはないでしょう.こういう状態では,多くの粒子の尤度(重み)は毎時刻それなりの値をとることになるでしょう.
一方,誘拐状態では,前の時刻まで「この辺りにロボットがいるはずだ」という信念のもとばら撒かれた粒子とは全然違う観測を得てしまうことになります.従って,この場合,多くの粒子の尤度(重み)は.安定状態の時のそれに比べて小さくなるはずです.この違いをウォッチしながら,誘拐状態の見極めを行うが,Augmented MCL のミソです.
そして,今誘拐状態であると判定された段階で,より広い範囲にランダムな粒子をばら撒くようなノイズ成分が,サンプリング時に混入されるのです.
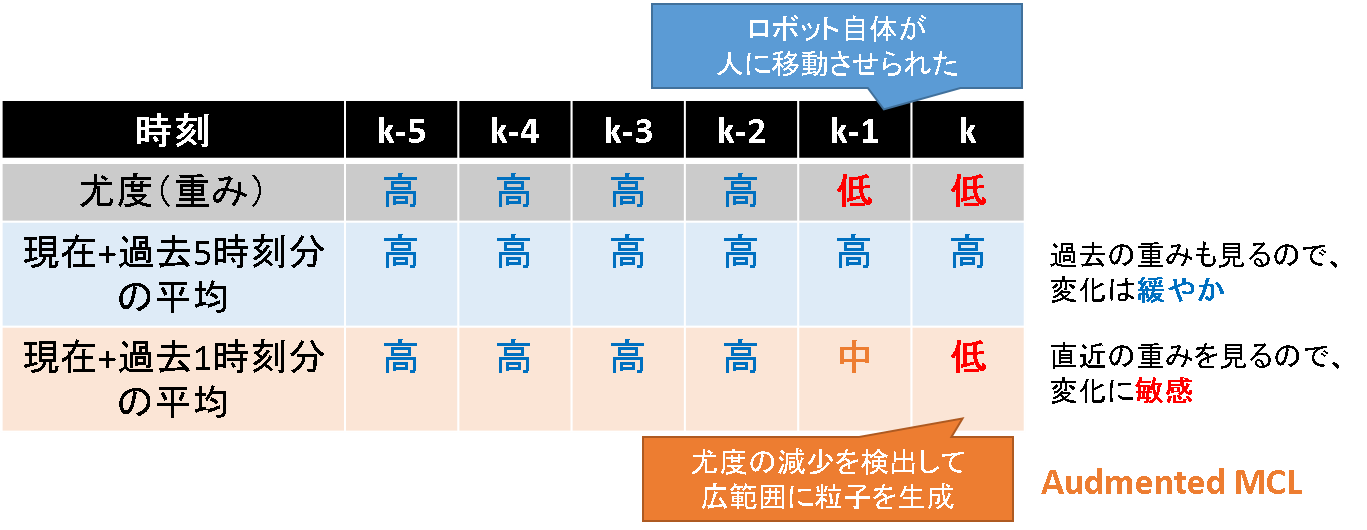
もう少し具体的には,上記尤度を長期間で平均したものと,短期間で平均したものの大きさを毎時刻比較していくことになります.下表の例では,時刻 k-1 においてロボットが誘拐されたことを想定しています.説明を簡単にするため,現在と過去5時刻分の平均を取る方を長期間の平均,現在と過去1時刻分の平均を取る方を短期間の平均としておきます.
まず過去5時刻から現在に渡って継続して安定状態であれば,これらの平均の差はさほど大きくはなりません.
一方,1時刻前でロボットが移動させられたとしましょう.すると,これらの平均値に変化が生じます.当然,長時間の平均を取る方では1時刻前に突然値が変化したところで急に値が変化することはありません.言わばローパスフィルタです.しかし,短時間の平均をとる方では,この影響をダイレクトに受けます.ここで,長期間の平均と短期間の平均間に大小の差が生じます.この差を検知して,前述したような粒子を配置する分布範囲の調整を行っているのです.
これは実際に誘拐問題に対しては良く働くようです.しかし,まだ悩みは尽きないというのです.安定状態の推定に使っていたときの粒子の一部を,上述したランダムなサンプリングのために割くのですが,粒子の数が足りないと思うように復帰ができ無い場合があるのです.誘拐された,というこれまで仮定をひっくり返されるほどのインパクトを,サンプルによる近似によって復帰させる以上,人海戦術が妥当です.だれかが誘拐されて探索範囲を広げる時ばかりでなく,プロジェクトが炎上しちゃって納期に間に合わなそうとか,お偉い方が訪問されるから厳重な警備が必要になったとかいうときに,人員補給をしたいと思うのは人の性ではないでしょうか.
それなら,粒子の数も増やしてしまえばいいじゃないか!という発想が出てくるは自然な流れです.そこで,KDL Sampling の登場です.
KLD Sampling
KLD Sampling では,粒子の分布状況に合わせて,その数を動的に決定するものです.アルゴリズムとして非常に単純なのですが,情報理論的な背景として,カルバックライブラー情報量(Kullback-Leibler Divergence) あるいは相対エントロピーと言われるパラメータを活用しているようです.
Probabilistic Roboticsによると,真の事後確率分布と,パーティクルフィルタによって標本ベースで近似された分布との違いを基に,その誤差が一定以下になるようにパーティクルの数を調整するというものらしいです.
直観的には,粒子が広範囲に存在するほど,近似誤差を小さくするためには粒子の数を増やす必要があるので,その近似誤差がある値を下回るまで粒子の数を増やし続ける,という処理を行います.一方,粒子の分布する範囲が小さくなれば,近似するために必要な粒子の数は少なくて済むので,今度は数を減らしていくという処理が行われます.
Probabilistic Roboticsでは情報理論を用いた証明は割愛されています.本手法の詳細に関心がある方は論文を参照下さい (Fox, Dieter. "KLD-sampling: Adaptive particle filters." Advances in neural information processing systems. 2001.).
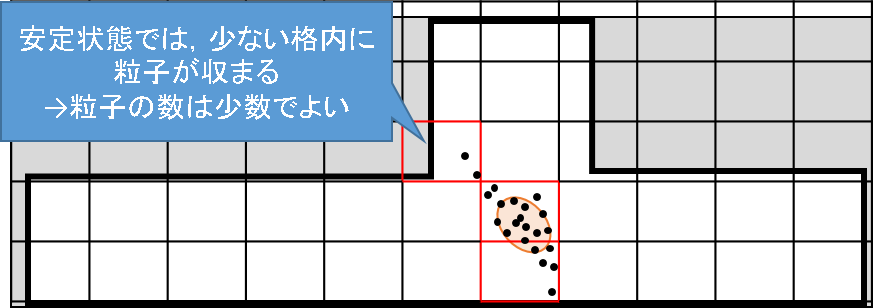
この挙動を図で理解してみます.まず,地図全体ある格子で分割しておき,これをヒストグラムのビンに対応させることにします.KLD Samplingでは,どれだけ多くのビンに粒子が登録されるかを見ることで,粒子の分布度合いを評価しているのです.
それでは,安定状態について見て行きます.この場合,粒子はある程度まとまった位置に分布するので登録されるビンは少数で済みます.粒子が少数であっても,カルバックライブラー情報量の値はそんなに大きくはなりません.したがって,粒子の数も増えません.
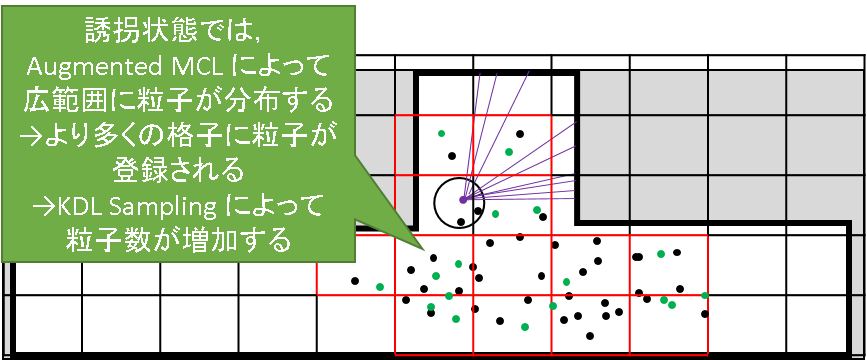
次に,誘拐状態を見てみます.誘拐状態になると,Audmented MCL によってランダムな粒子が広範囲にばら撒かれていくことは,前節で確認しました.すると,より多くの格子内に粒子が存在することとなり,占有されるビンの数が増加します.このままでは,近似誤差を十分に小さくするために必要な粒子が足りていないため,カルバックライブラー情報量の値が大きくなってしまいます.そこで,粒子の数を増やして,近似精度を高めようというわけです.
安定状態から誘拐状態へ遷移したとのイメージをまとめたものが下図になります.
一方,誘拐状態から復帰したとします.今度は逆に,粒子が安定状態に向かうため,粒子の分布の広がりがなくなります.すると,近似に必要な粒子の数も減少するので,不要な粒子を消去していきます.
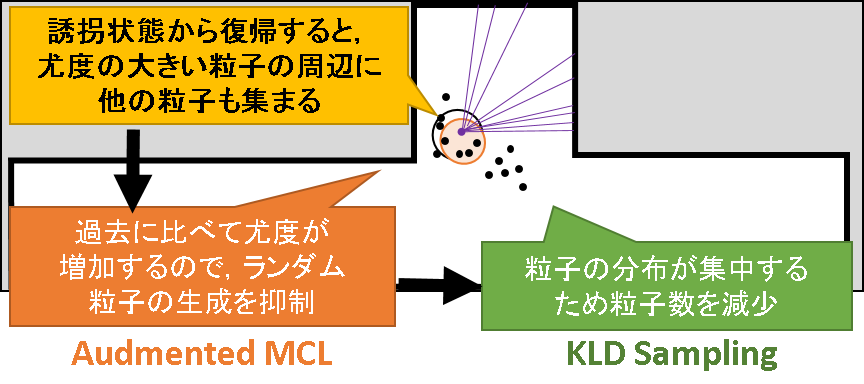
なんと都合のよい仕様なのでしょう.安定しているときは粒子を減らしてサクサク計算で惰性的な自己位置推定をして,緊急に必要な時だけ粒子を増やして丁寧に探索を行い状態復帰を図る,という動作が実現できるのです.しかも,理論的な裏付けまでできている.これは素晴らしいですね.
おわりに
以上が,amcl のメインフローです.おさらいをしておきましょう.
- 自己位置推定の基本フロー(パーティクルフィルタの一般的なフロー)
- オドメトリによる事前推定 → サンプリングで粒子をばら撒く
- 観測に基づく尤度の計算 → 粒子の重みづけ
- 推定値の算出 → amcl では最大重み推定
- amcl の技巧的処理
- 尤度モデル
- 定常的なノイズ成分 → センサ値を中心としたガウス分布
- 障害物対策のノイズ成分 → センサ値よりも短距離部分に値を持たせる
- 乱反射対策のノイズ成分 → センサ値の最大値に値を持たせる
- 誘拐対策のノイズ成分 → 観測範囲全域に値を持たせる
- サンプリング
- Augmented MCL → 誘拐されたらランダムサンプリング数を増やす
- KLD Sampling → 粒子が広範囲に分布したら数を増やす
すごいです.各構成要素が相互に連携しており,よく考えられた構成となっているのです.しかも理論的なお墨付きです.これが2005年に書かれた書籍のお話なのです.論文ベースでは,更に早い段階で実現されていたのです.まだ私が鼻たれ小僧だった時に,世界の天才研究者はこんなところまでいたのですね.それを理解するだけでこんなに苦労している私っていったい…
とにかく,パーティクルフィルタがこんなに奥深いものであること知ることができたのは,ひとえにProbabilistic Roboticsと,amclのコードのおかげです.私のようなしがないサラリーマンでも,こんな技術の一端を学ぶことができたのです.いい時代に生まれたのかもしれません.
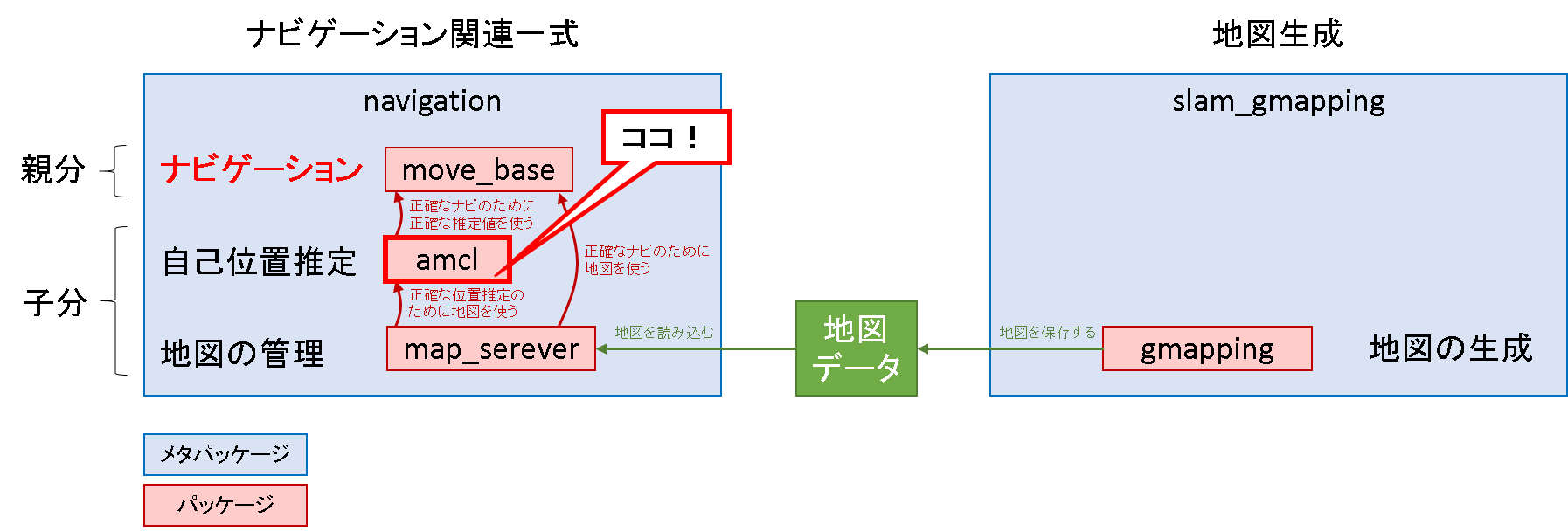
さて,そんな感情に浸ってばかりもいられません.ここでは,「地図は天から降ってきたもの」という仮定を置いていたことを忘れてはいけません.誰が地図を作ってくれているのでしょう?
そうです.SLAM くんです.自己位置推定と地図作成を同時に行う方法です.Probabilistic Roboticsの神髄はここにあるといっても過言ではありません.
次回以降,Fast SLAM を扱っていこうと思います.ただし,ROSの"ros-perception/slam_gmapping", github.をベースとします.gmapping ではパーティクルフィルタ+格子ベースのFast SLAM が実装されているので,拡張カルマンフィルタ+ランドマークベースのProbabilistic Robotics版Fast SLAM とは話が変わってきます.しかし,本質となる理論は共通です.
Probabilistic Roboticsの解説と,ここまで学んだパーティクルフィルタによる自己位置推定の知識をベースに,いよいよSLAM の世界に踏み込もうというわけです.
と書いてしまったけど,自分にできるかな….若干そんな感情は抱いていますが,まぁアウトプットする過程で私自身も学ぶことになると思うので,取りあえず前向きに進んでみようと思います.^^
またその時が来たらツラツラと書こうと思います.それでは!
Next: 4.1 gmapping: ROSで遊んでみる
Prev: 3.4 amcl: 原理をみる (準備編)