目次
- 導入
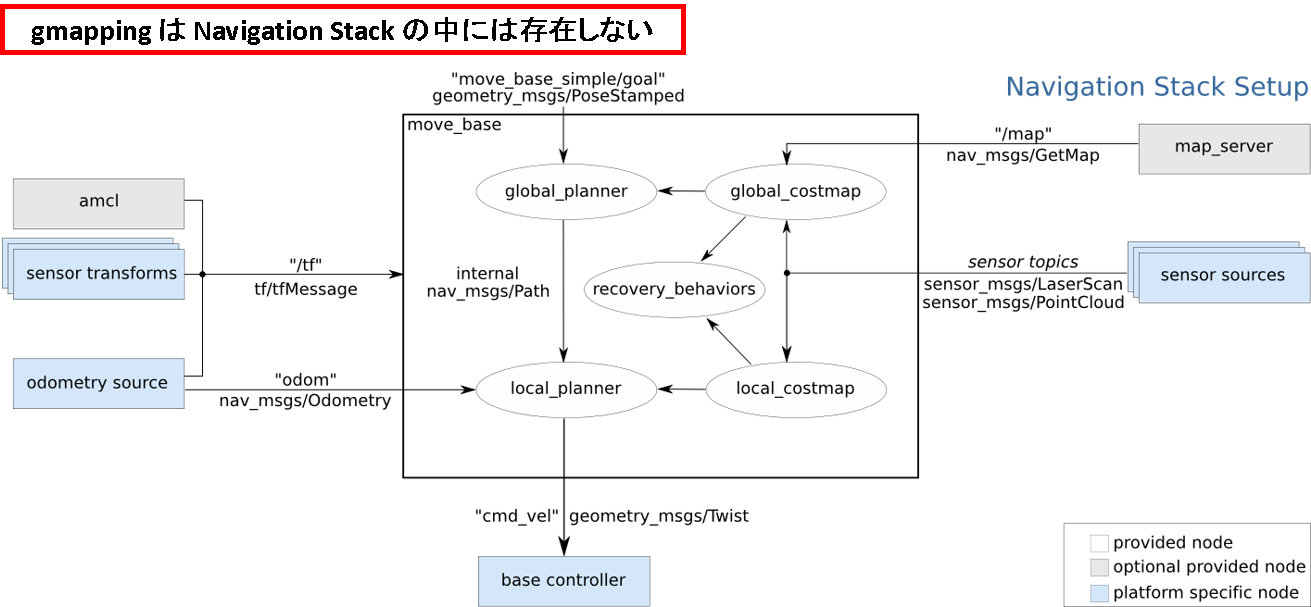
- move_base (ナビゲーション)
- ROSで遊んでみる
- ソフトウェア構成をみる
- amcl (自己位置推定)
- ROSで遊んでみる
- ソフトウェア構成をみる
- 原理をみる (準備編)
- 原理をみる (応用編)
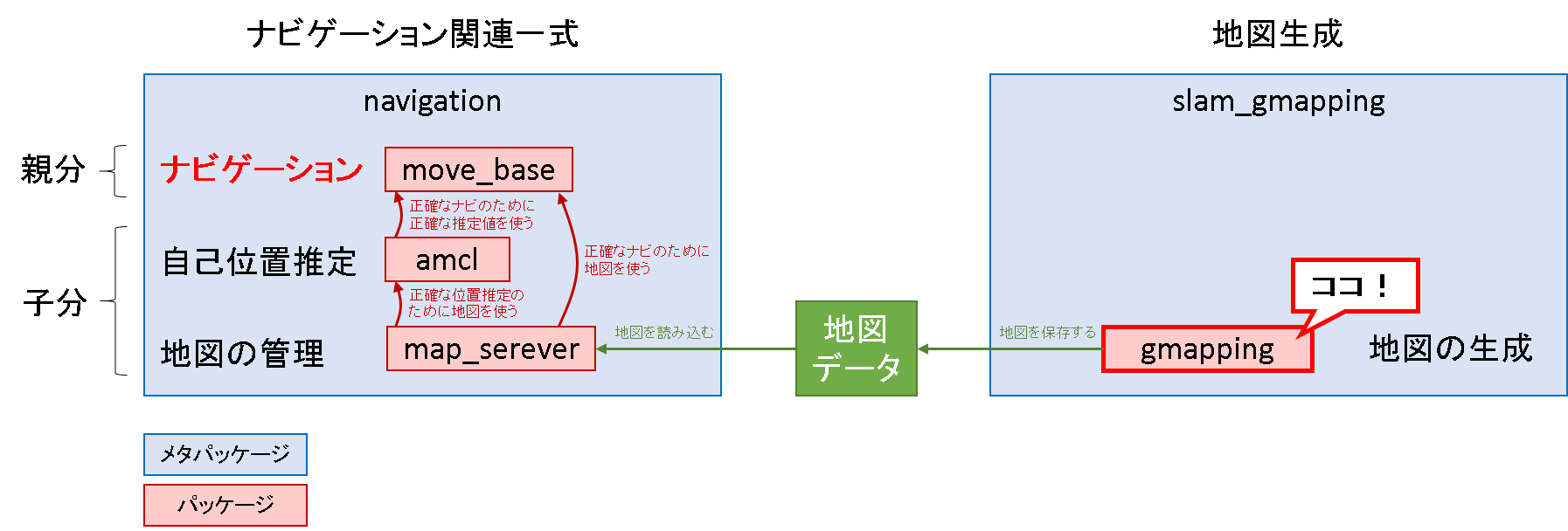
- gmapping (地図生成)
- ROSで遊んでみる
- ソフトウェア構成をみる
- 原理をみる(応用編) ← いまココ
- 原理をみる(準備編 その1)
- 原理をみる(準備編 その2)
はじめに
Navigation Stack を理解する - 4.2 gmapping: ソフトウェア構成をみるの続きです.頑張っているgmappingの中で何が起きているのかを見ていきます.
主に参考とした文献は下記の2です.
- 特徴ベースFast SLAM の基本理論,Rao-Blackwell 化,有占格子地図 等
- 格子ベースFast SLAM の元論文(gmappingはこれを実装)
本シリーズでは,数式ガチャガチャのイメージが強いSLAM 問題に必要な技術について,できるだけ数式を排除してイラストを用いて直観的に理解できるように記述することを心がけています.しかし,SLAM 問題に入り込もうと思うと,数式を完全に排除して説明しようとすると雲をつかむような議論となってしまいます.
そこで,本編においては,Fast SLAM で扱う数式と向かい合いながら,その数式の背後にある原理や,それによって実世界での動作に与える影響を考察していくこととします.いわば,Fast SLAM の数式に対するリバースエンジニアリングです.従って,数式の証明自体は追ったりはしません.解析的な証明は,それこそ様々な文献に記述されているので,そちらに譲ることとします.
本編の構成
- 応用編
- Fast SLAM 1.0
- イラストによる挙動の理解
- 数式との対応
- Fast SLAM 2.0
- FastSLAM 1.0 との比較(イラスト版)
- FastSLAM 1.0 との比較(数式版)
- 特徴ベースから格子ベースへの展開
- 準備編 その1
- Fast SLAM の基本フロー
- Rao-Blackwell 化
- 準備編 その2
- オンラインSLAMと完全SLAM
- 有占格子地図
本編においても,3.3 amcl: 原理をみる (準備編)と3.4 amcl: 原理をみる (応用編)と同様に,準備編と応用編に分けて説明をしていきます.ただし,最初に応用編,その後に準備編です.
え?先に応用?となりますよね.実は,準備編を書いていたら随分と紛糾をしてしまい,本当に面白いSLAMの挙動にたどり着くまでに疲れてしまうことは必至だと思ったのです.
だから,まずは応用上どのような挙動になるのかをイラストで先に確認しちゃったほうが,頭に入りやすいと思ったのです.そのイラストの背後にある数式は本稿後半に記してあります.更に,FastSLAM アルゴリズム全体を理論付けるより詳細な背景を知りたくなった人だけが,次回以降の準備編を見てみればよいと思ったのです.この辺は,退屈な感じは否めないので^^;
では,本題に移ります.
概要
扱うSLAMは,ROSの"gmapping"で実装されているFastSLAM です.なお,内部的には"gmapping", OpenSLAMをラップしているものとなっています.
FastSLAM のざっくりとしたフローを確認しておきます.注意点も含めた詳細は次回述べることとして,ここでは早くイラストにいってしまいましょう.青い吹き出してコメントした部分は,FastSLAM 2.0でのみ扱う点です.1.0 と 2.0 を順番に説明する過程で,詳細を説明します.
- 「注意点も含めた詳細」については,「4.3. 準備編 その1 Fast SLAM の基本フロー」で述べる予定です.
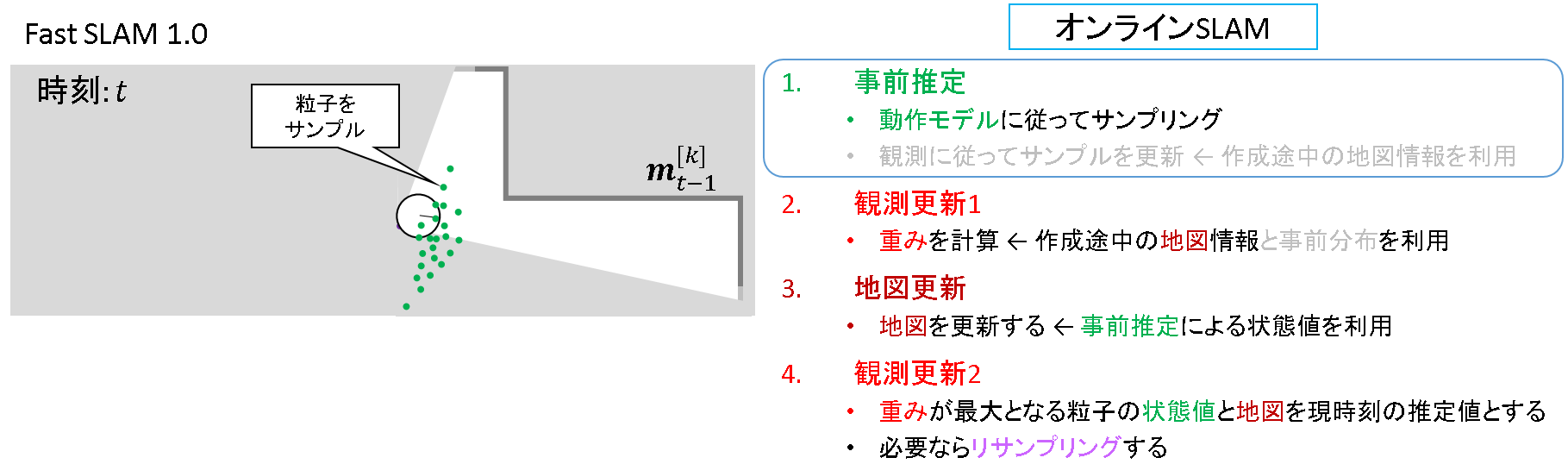
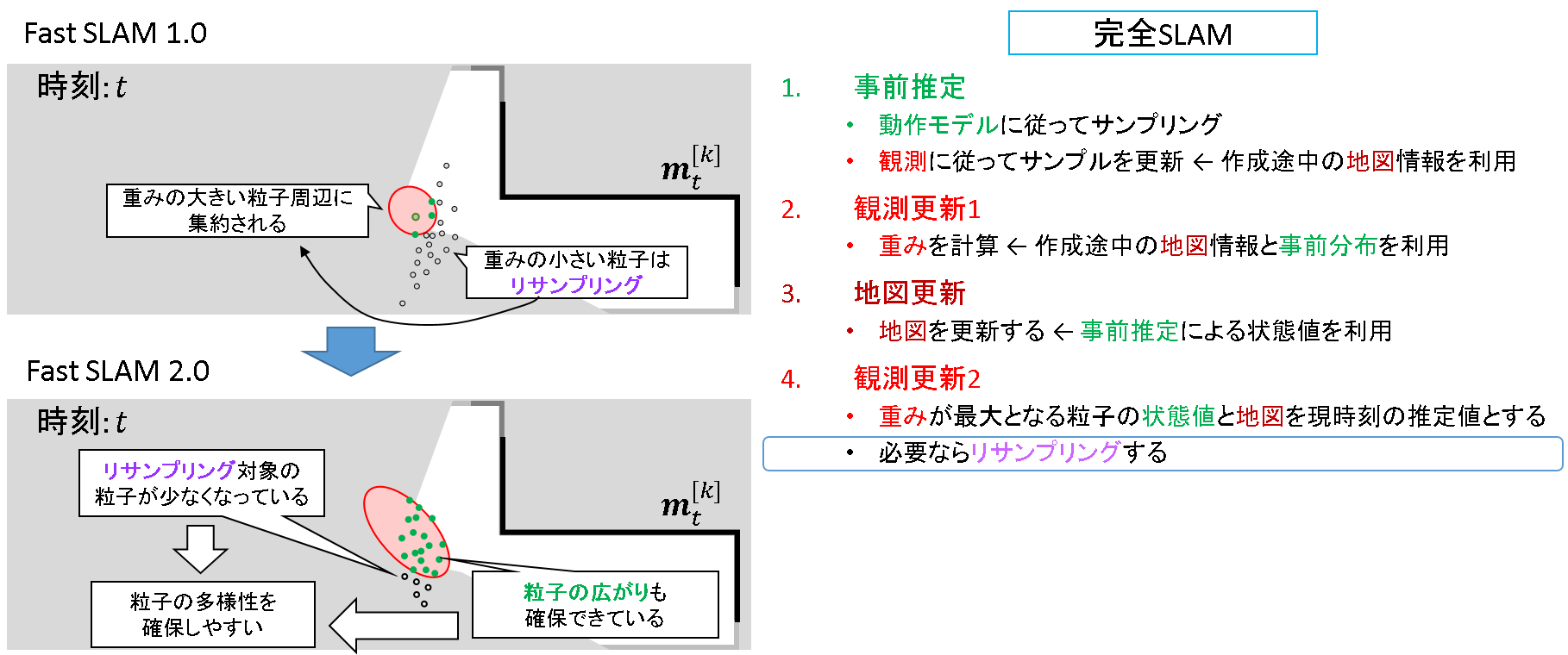
Fast SLAM 1.0
それでは、FastSLAM 1.0 の挙動をイラストで解釈していきましょう。
一応前提の確認です.時刻tでロボットが移動しています.今使える地図は,時刻t-1までに作成された中途半端なものです.この状態で,ロボットの位置と地図を更新したいのです.
イラストによる挙動の理解
ステップ1: 事前推定
動作モデルに従って粒子をばら撒きます.「オンラインSLAM問題」がキーワードとなります.FastSLAM 1.0では観測による更新は行いません.このまま次のステップに進みます.
- 「オンラインSLAM問題」については,「4.4. 準備編 その2 オンラインSLAMと完全SLAM」で述べる予定です.
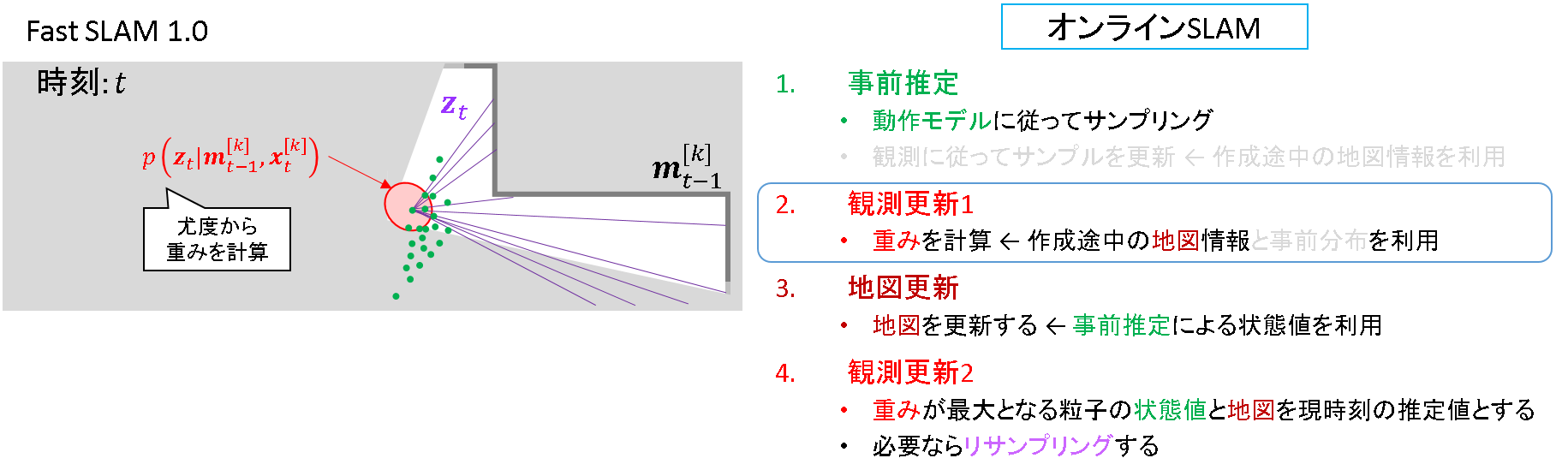
ステップ2: 観測更新1
観測と作成途中の地図を元に尤度を計算し,各粒子の重みを更新します.ここでも「オンラインSLAM」がキーワードとなります.FastSLAM1.0では事前分布の情報は使いません.
- 「オンラインSLAM問題」については,「4.4. 準備編 その2 オンラインSLAMと完全SLAM」で述べる予定です.
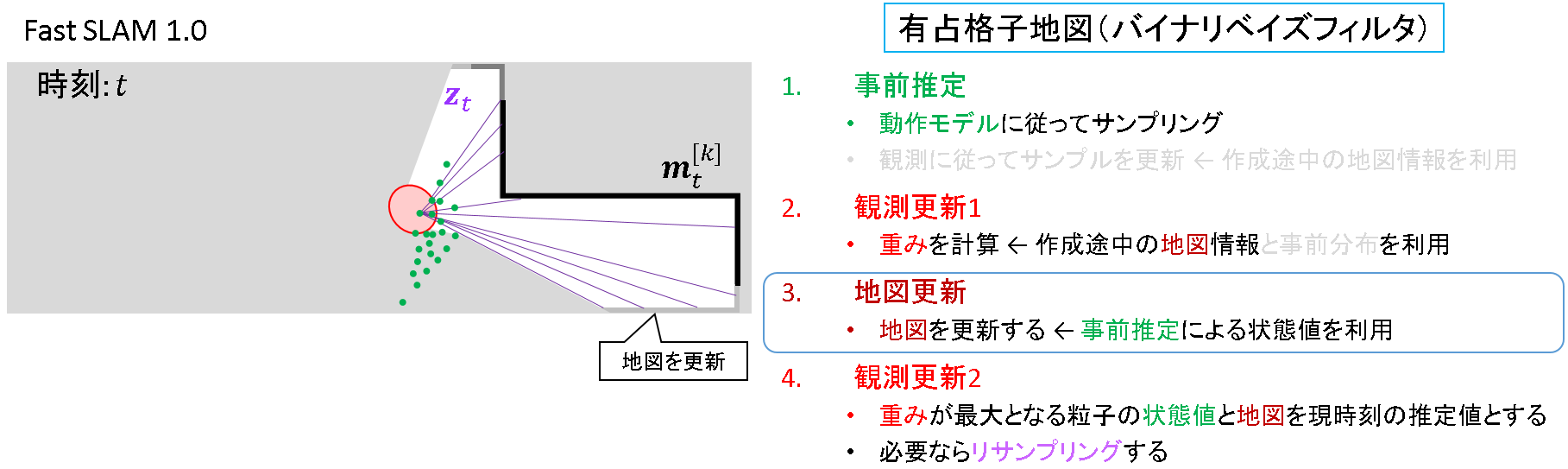
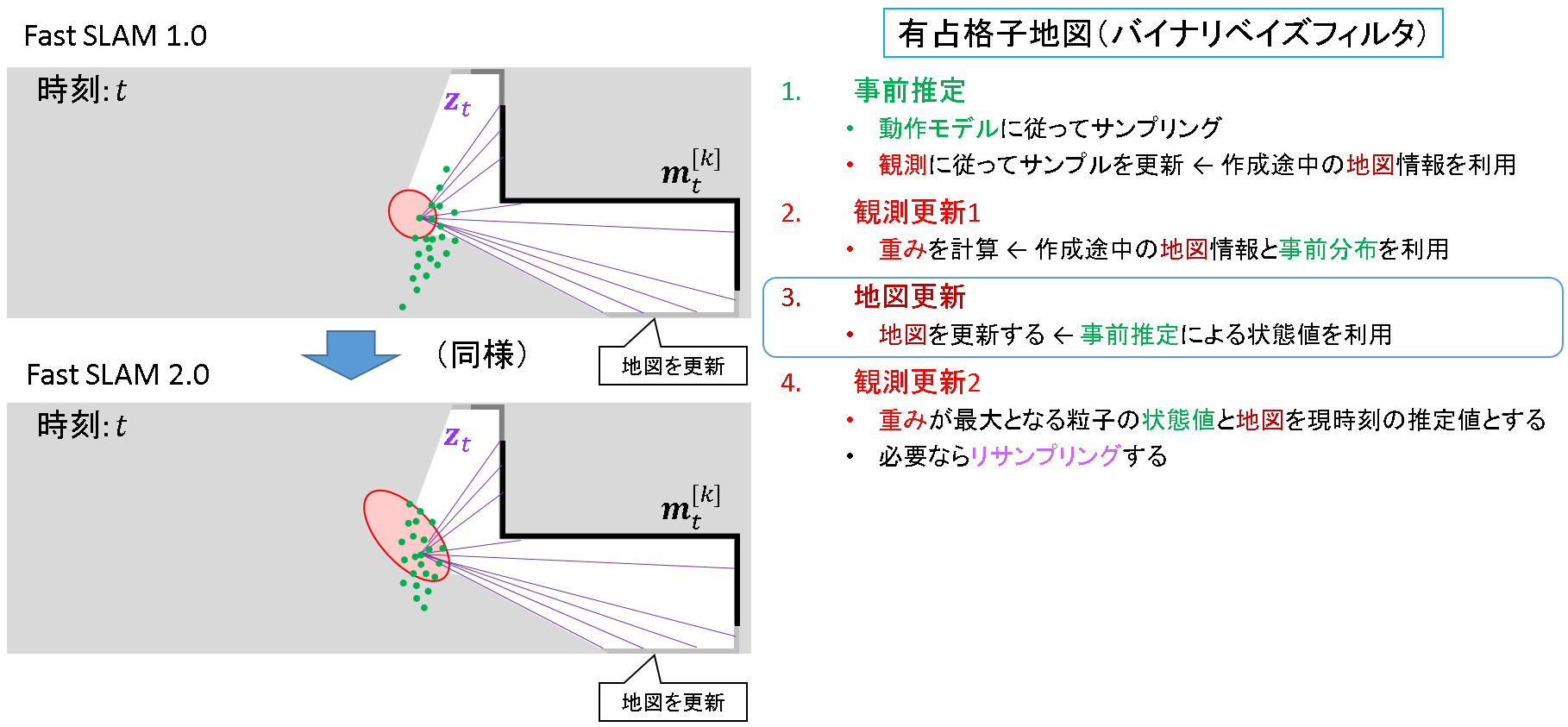
ステップ3: 地図更新
リサンプリングの前に地図を更新します.「有占格子地図」がキーワードとなります.このとき,粒子毎に異なる地図を持つことになります.状態が異なるN個粒子があれば,N種類の地図が出来上がることになります.この点については,「Rao-Blackwel 化」がキーワードとなります.
- 「有占格子地図」については,「4.4. 準備編 その2 有占格子地図」で述べる予定です.
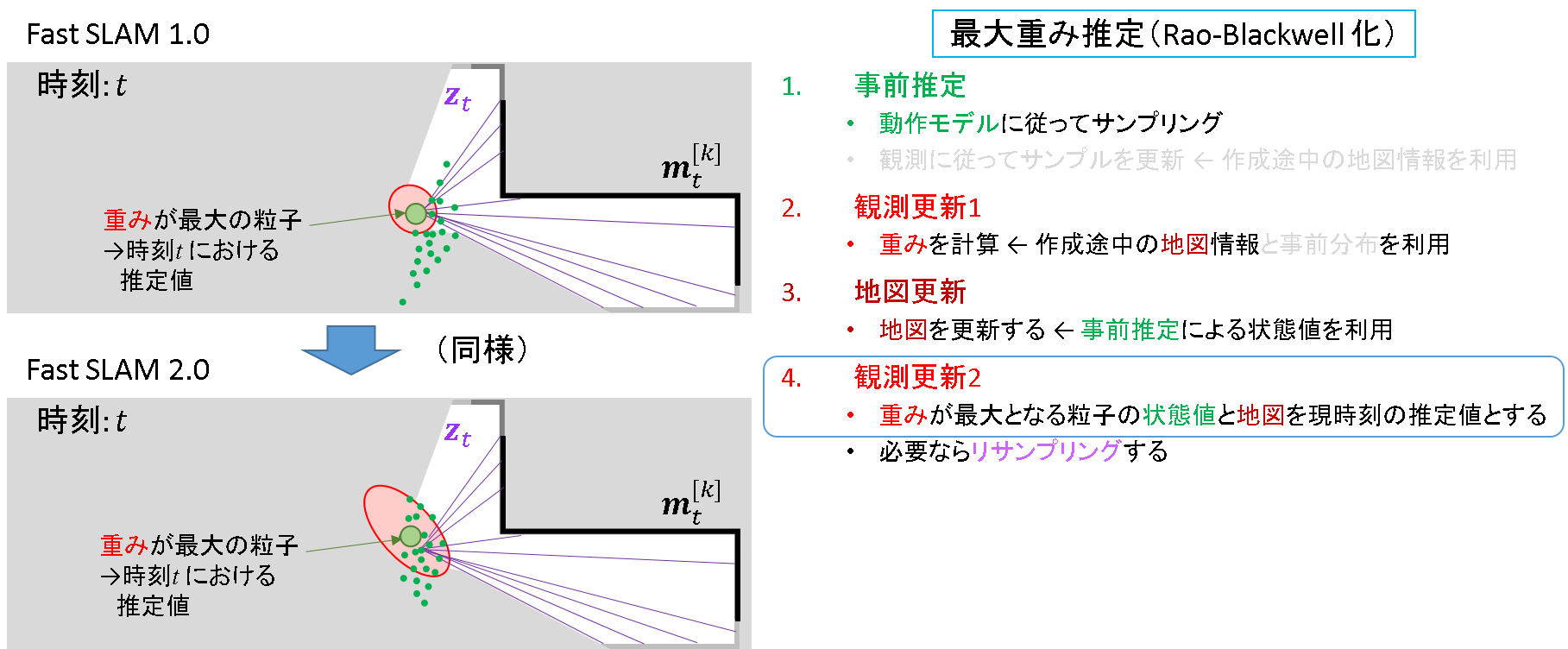
ステップ4: 観測更新2
地図を更新した後に,現時刻の推定値を確定します.このとき最大重み推定を行うことは,「Rao-Blackwell化」と関係することになります.
- 「注意点も含めた詳細」については,「4.3. 準備編 その1 Rao-Blackwell化」で述べる予定です.
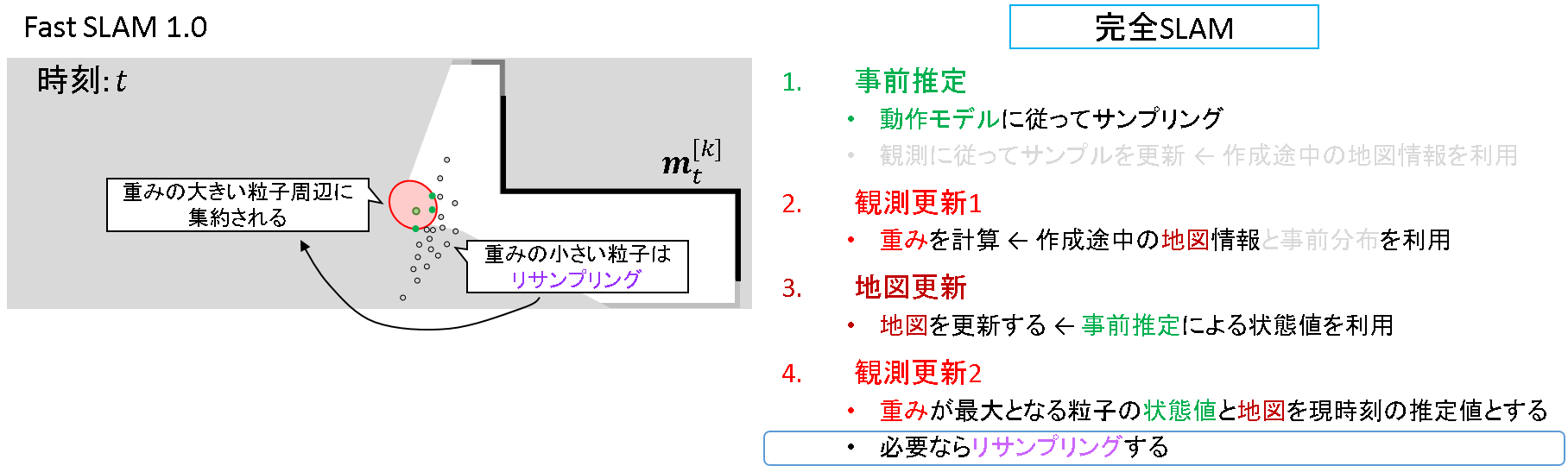
その後リサンプリングを行います.ここが「完全SLAM問題」と関連すると,解釈しました.※この点は当方の考察です.
- 「完全SLAM問題」については,「4.4. 準備編 その2 オンラインSLAMと完全SLAM」で述べる予定です.
さて,リサンプリングによって重みの大きい粒子だけを生き残らせるのですが,上図では生き残れそうな粒子が少ないのが分かると思います.これは,粒子は観測とは関係ない方向にばらまかれること,重み関数の分散が小さく生き残らせられる粒子が少ないという点が原因と考えられます.これでは,粒子の多様性や動作モデルの分布に関する情報が失われ,パーティクルフィルタの特性を有効活用できなくなってしまいます.
じゃあ,「粒子をもっと観測に近い方にばらまいて」,かつ「重み関数の分散を大きくして粒子をすくう網を広げれば良い」ではないか,という発想が生まれます.この発想が,FastSLAM 2.0 における式展開へと繋がるのです.
数式との対応
ここで,数式との対応を見てみましょう.ただし,ここでは特徴ベースでの式展開を扱います.
いいわけ
イラストについて散々格子ベースを扱ってきたくせに,ここで特徴ベースを出すだなんて言うちゃぶ台返しをするのは,ひとえに私の力不足故です.Probabilistic Robotics のFastSLAM 1.0と2.0は特徴ベースなので,これに全面的に依存することにしたのです.
今からやりたいのは,これらの特長を比較することなのですが,格子ベースだとFastSLAM 2.0しか見つからなかったので,これを直接1.0 → 2.0に展開させるのは控えたいのです(これを自信を持ってできない点が,私の力不足に他なりません).文献ベースで証明されている情報を基にリバースエンジニアリングをしたいのです.
そこで,まずは数式については特徴ベースでFastSLAM 1.0 → 2.0へ展開させます.その後,FastSLAM 2.0 において特徴ベース → 格子ベースへと展開させていくことにします.
数式
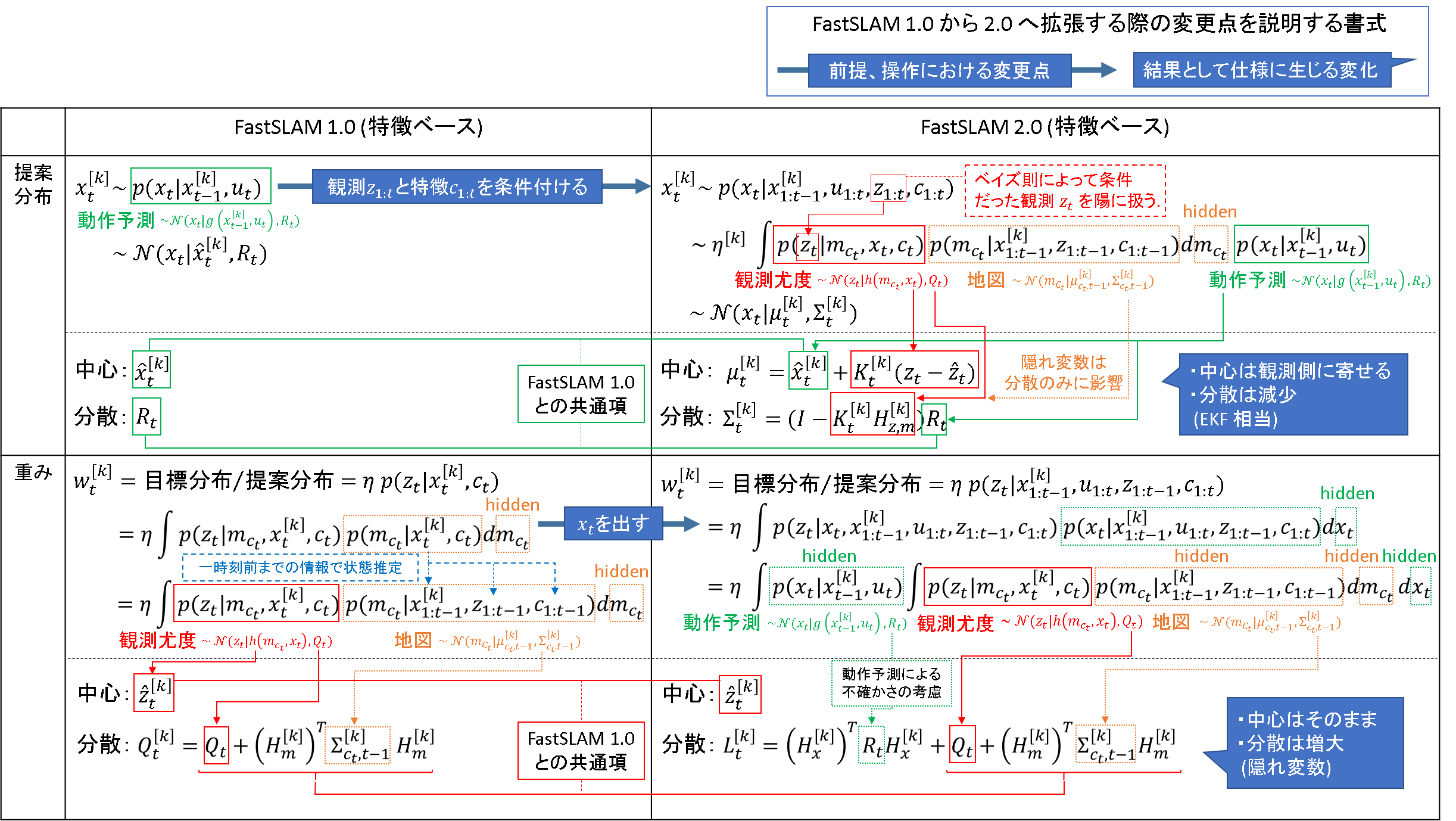
それでは,まずざっと特徴ベースFastSLAM 1.0の式を確認します.変数の説明,解析的証明等はProbabilistic Roboticsに預け,結論だけを抜粋します.ここではざっと数式と挙動の対応関係を掴みたいのです.また,FastSLAM 1.0 → 2.0への展開を理解する上で,大事なのは「提案分布」と「重み」ですので,これらの式だけを抜粋します.
ごちゃっとしてしまいましたが,ここで把握しておくべきことを下記のとおりです.
- 提案分布
- 中心も分散も「動作モデル」に従う
- 重み
- 隠れていた「地図」に関する変数を表舞台に出している
- 中心は「観測モデル」に従う
- 分散は「観測」の不確かさ+「地図」の不確かさの重ね合わせである
提案分布の方はこれまでの自己位置推定と同様ですが,重みがちょっと変わります.重みの式では周辺化されていたはずの隠れていた変数「地図」をワザワザ取り扱うように式を変形しています.こうすると,ランドマークの位置推定の誤差を重みの計算式で陽に扱うことができるのです.
ここで注目すべきが,隠れ変数「地図」を出すと,重みの「中心」には影響を与えず,「分散」にだけ影響をあたえると言う点です.「分散」が大きくなる点は,どこの馬の骨とも知らない変数を突然出てきたのだから不確かさが増すのは当然だろう.ただし,その隠れ変数で積分したら元の重みの数式に戻るような分布を形成しているはずなのだから,「中心」まで変えるのはおかしい.直観的にはそんな感じかな,と解釈しています.
この感覚は,FastSLAM 1.0 → 2.0 への展開を理解する上で非常に重要なので,ここで述べておきました.
FastSLAM 2.0
それでは,ここからはFastSLAM 2.0 の話に進みます.FastSLAM 1.0と比較して,何がどう良くなっているのかに着目しながら説明をします.まずはぱっと見て理解できるようにイラストを,次にそのイラストの挙動の背景に潜む原理を見るために数式を比較する,という順で構成します.
FastSLAM 1.0 との比較(イラスト版)
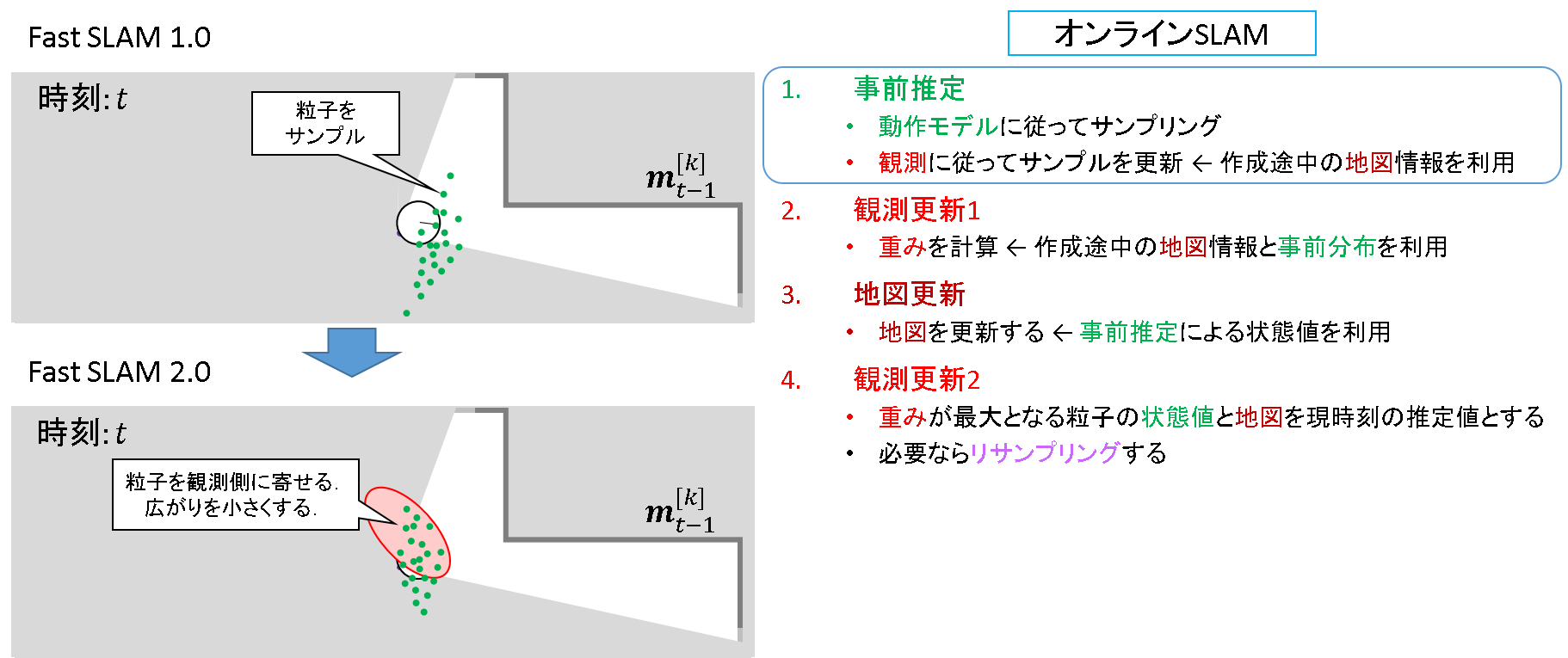
ステップ1: 事前推定
FastSLAM 1.0 では動作モデルによるサンプルをして終了でした.FastSLAM 2.0では,ここで観測を使うのです.粒子をどうばらまくか,といいう提案分布の仮定が変わっています.
粒子を撒く,観測する,更新する.そうです,カルマンフィルタで言うところの観測更新までもう既にここで行っているのです.これにより,「粒子のばらまく位置を観測寄りにできないか」というFastSLAM 1.0 の問題提起に対する対策がなされています.ただし,作成途中の不確かな地図を使っているから誤差は載る,ということは特性として理解しておくべきだと思います.
粒子のばらまく位置を観測寄りにする,という点に関する直観的な理解は,下記記事に譲ります.
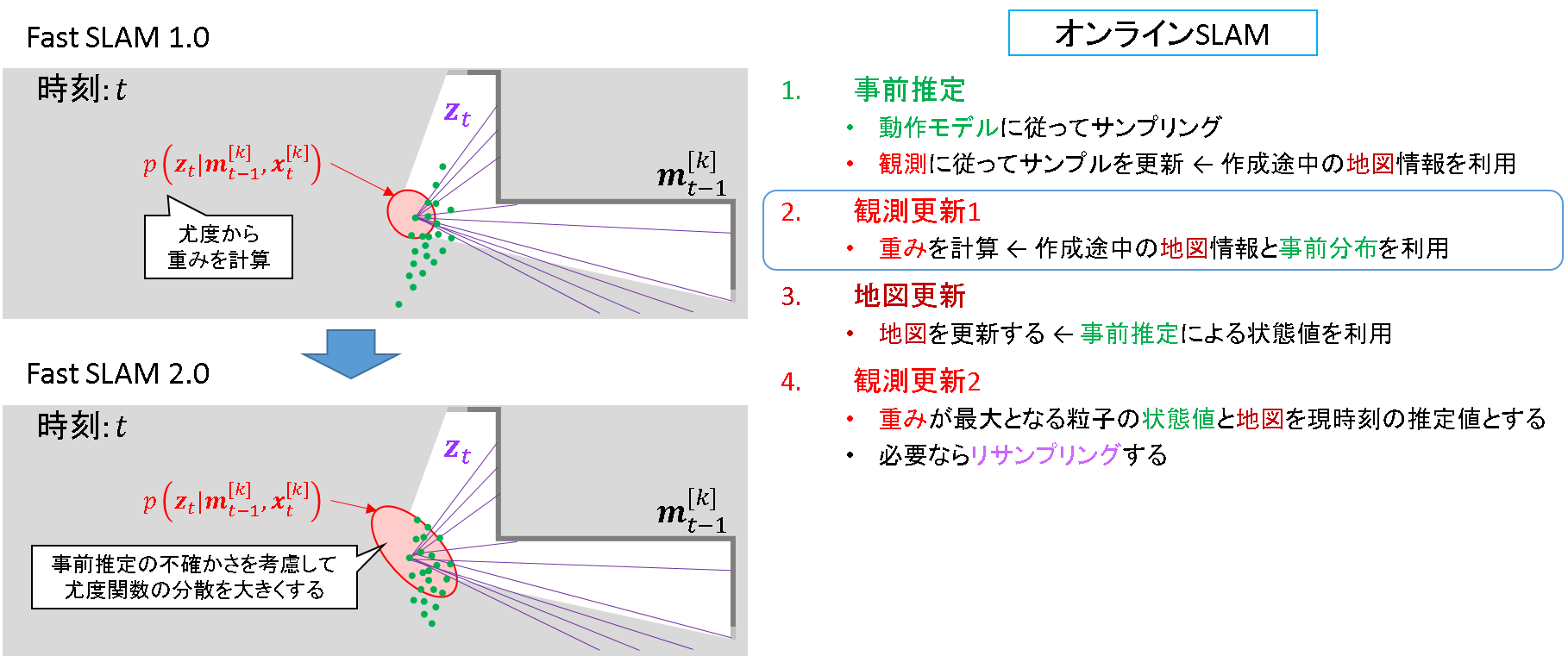
ステップ2: 観測更新1
FastSLAM 1.0 における重み計算式は,観測モデルと地図の不確かさの重ね合わせでした.FastSLAM 2.0ではここに「動作モデル」の不確かさを組み込んでいるのです.重みの関数がより多くの粒子を包含しそうな予感がします.「重み関数の分散を大きくして粒子をすくう網を広げれば良い」というFastSLAM 1.0 の問題提起に対する対策がなされています.
観測値によって決定づけられるべき重み分布の「中心」に影響を与えることなく,「分散」だけを広げるのです.どこかで聞きましたね.FastSLAM 1.0 の数式の部分で触れた,「隠れ変数」が関係してきそうな予感がしてします.それは後述することにします.
ステップ3: 地図更新
ここはFastSLAM 1.0と同様です.
ステップ4: 観測更新2
リサンプリングするときには,FastSLAM 1.0 の時よりも多くの粒子が生き残ります.これは,「粒子をもっと観測に近い方にばらまいて」,かつ「重み関数の分散を大きくして粒子をすくう網を広げれば良い」ではないか?という当初の発想を基に,「事前推定」と「重み関数」について改善が施されているからです.
こうすることで,動作モデルの分布をある程度保存することができ,本来のベイズフィルタの理論に従った挙動を実現できると言えるでしょう.
FastSLAM 1.0 との比較(数式版)
良いこと尽くめに見えるFastSLAM 2.0ですが,代償はその数式の複雑さです.それはもう初見では目を背けたくなるようなものでした笑(学生失格…).
でも,それは偉大なる先人がスマートに証明してくれているので私のような凡人はありがたく使わせて頂けばよいわけです.が,全く理解しないというのも恐れ多い.ということで,もう少し理解してみようと思うのです.FastSLAM 1.0 と 2.0 を比較しながら,FastSLAM 2.0 の特長を解釈していきましょう.
数式展開自体を理解するのは,文献を見ながら個人のペースでじっくりと取り組むのが一番です.(理解のペースや持っている前提知識,はたまた目指している理解レベルも人によっててんでバラバラなのだから,あれは人とやるものではないと思っている笑.)
ここでは,特長を比較する上で必要な要素に絞って列挙します.
- 提案分布
- 「観測情報」を提案分布の条件として陽に扱うように変更する
- 中心も分散も「動作モデル」と「観測モデル」によるフィルタリングによって決定される
- 「拡張カルマンフィルタ」のような操作が行われていると解釈できる
- 重み
- 隠れていた「状態」と「地図」に関する変数を表舞台に出している
- このうち,「状態」を陽に扱えるようにしたことがFastSLAM 2.0 における工夫点である
- 中心は「観測モデル」に従う
- 分散は「観測」の不確かさ+「地図」の不確かさ,さらに「事前推定」の不確かさまで重ね合わせたものである
提案分布では,粒子を観測側に「移動」させたかったはずです.分布の「中心」を変えようと思うと,理論的にはベイズフィルタをかけるしかありません.だから,確率密度関数の条件付けを変えてしまったのです.これは,提案分布は設計者がある程度任意に設定できるというパーティクルフィルタの基本理論の特性をうまく利用したと解釈できます.
一方重みでは,分散を広げたかったのです.でも,重み式の構造は提案分布に依存するものなのでで,これは提案分布ほどの設計自由度がありません(ただし,1.0 と 2.0 で重みの式が少し違うように見えますが,本質的には同等なのです.).じゃあ,どうするか?それなら,重みの計算の背後には実は「時刻tの状態変数」が潜在していて,それが周辺化していたから隠れていただけだ,と解釈して無理やり(?)表に出してしまおうと言うわけです.これを計算すると「分散」だけが各分布の重ねあわせになるような結果が得られるのです.ある分布を決定づける上で必要な変数が増えるのだから,不確かさが増すという事実は,直観的にも矛盾はないと思います.
こうして今一度数式を眺めると,FastSLAM 1.0 → 2.0 で何を改善するためのどう数式を変換したのかが,感覚的に分かってきたような気がしてきませんか?^^
特徴ベースから格子ベースへの展開
ここで,"Probabilistic Robotics"の特徴ベースFastSLAM
2.0の式と,"Improved techniques for grid mapping with rao-blackwellized particle filters."の更新ベースFastSLAM 2.0の式を比較してみます.
本質的にやりたいことは同じなのですが,地図の形式が変化している影響で若干式が変わっていきます.
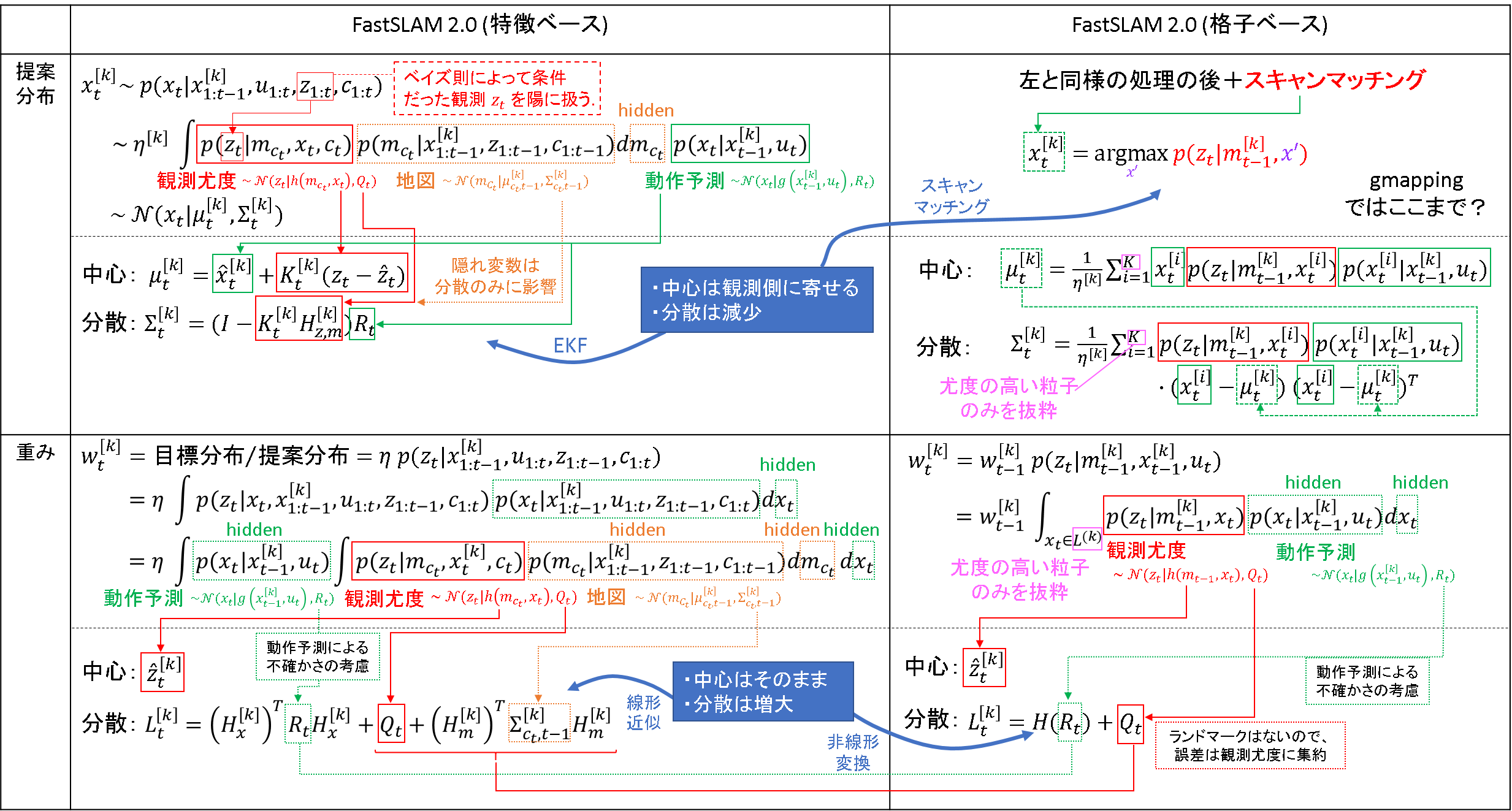
- 提案分布
- 「観測情報」を提案分布の条件として陽に扱う(特徴ベースと同様)
- 中心も分散も「動作モデル」と「観測モデル」によるフィルタリングによって決定される(特徴ベースと同様)
- ただし,その方法がカルマンフィルタではなく,スキャンマッチングと粒子による近似計算となる(格子ベースでの変更点)
- 地図の不確かさは尤度関数の中で周辺化させたままにする(格子ベースでの変更点)
- ランドマークの位置推定をしているのではなく壁の有無に関するバイナリベイズフィルタを解いており,分散を評価するのが難しい
- 重み
- 隠れていた「状態」に関する変数を表舞台に出している
- 「地図」は周辺化させたままとする(格子ベースでの変更点)
- 中心は「観測モデル」に従う(特徴ベースと同様)
- 分散は「観測」の不確かさ+「事前推定」の不確かさの重ね合わせとなる
- ただし,分散の写像は何らかの非線形関数.実装上は計算の必要はない.分散がどうなるかは粒子をばらまいた結果でしかない.
提案分布での変更点について
「提案分布」での変更点のミソは,「地図」が周辺化されたままであること,「スキャンマッチング」を行うこと,分布の計算で「粒子による近似」計算が行われることです.「地図」が放置された経緯は,上述した理由と推察しています."Improved techniques for grid mapping with rao-blackwellized particle filters."ではこの隠れ変数を出すような操作は確認できません.中心と分散の計算式が積分ではなくて総和になっているのは,この後の説明をしやすくするために,粒子を扱うための最終的な式展開の形を載せたという経緯があります.(もちろん大本の式は積分で,粒子で離散化されているから総和に変換する,というプロセスが背後にはあります.)
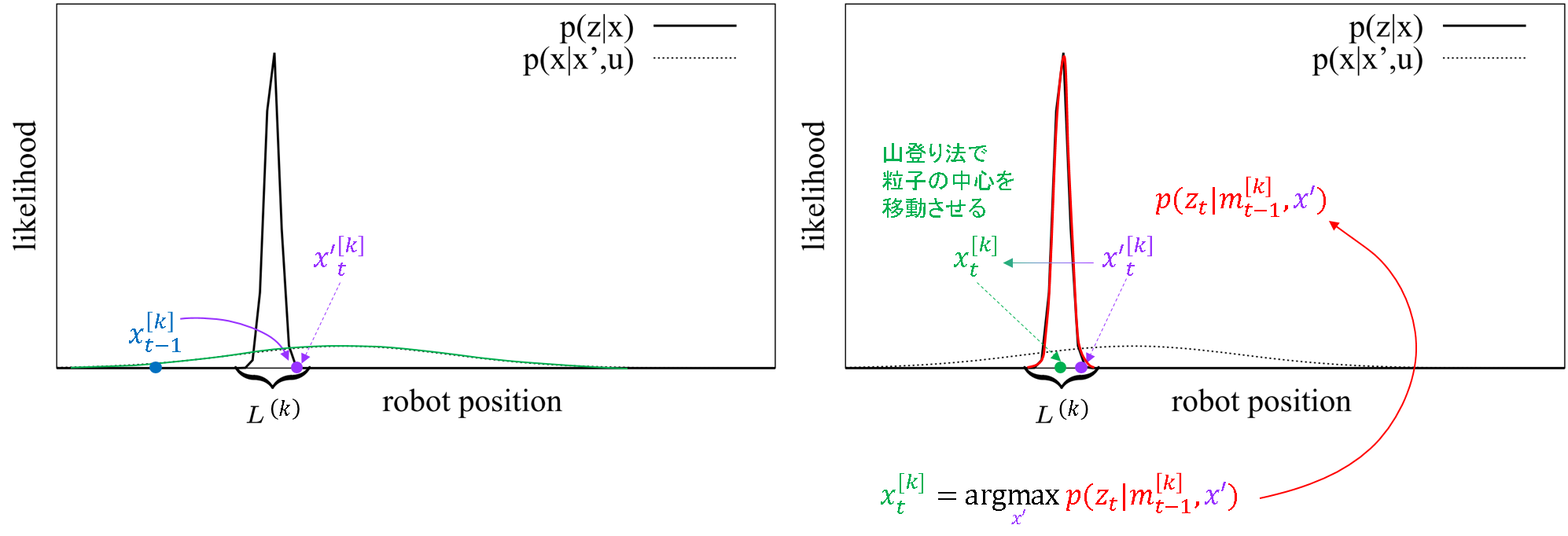
「スキャンマッチング」以降の理解について,1次元にしてちょっとイラストで見てみます.下地の図は,"Improved techniques for grid mapping with rao-blackwellized particle filters."を参照しています.
- まず,動作モデルに従って粒子を移動させます.でも,これでは終わりません.
- ここですぐに観測情報を使います.動作モデルで移動させた粒子を,今度は尤度が高くなる位置に移動させます.gmapping では,山登り法を使っているようです.
- 特徴ベースではこれをカルマンフィルタで行っています.格子ベースではランドマークで位置推定をしているわけではなく,よくわからない非線形な地図を扱う必要があります.そういう地図だとカルマンフィルタのようにカチッと計算式で更新するのは難しいので,こういう力づくな方法を使っているのでしょう.
- こうなると,バイナリベイズフィルタベースの地図の不確かさを陽に扱うのはやっぱり難しいのでしょう.
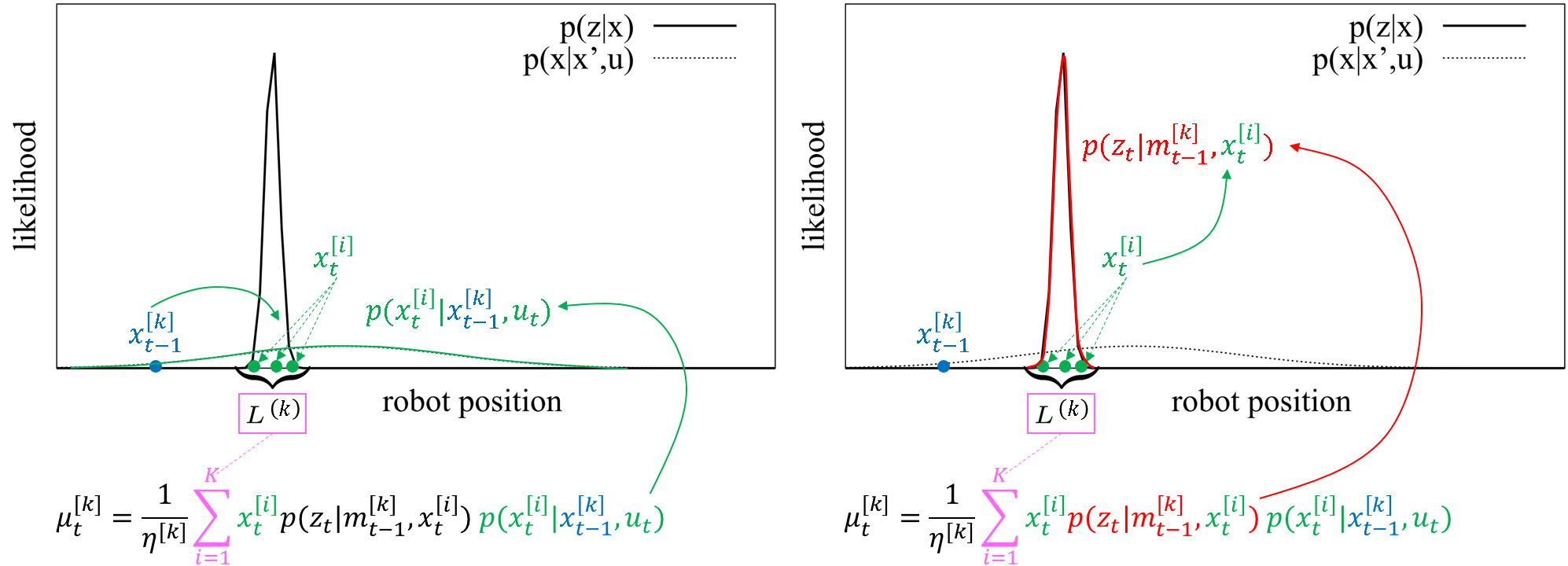
- でも,論文中ではこうして求めた粒子の位置はまだ「仮の」位置としているのです.更に,周りの粒子との分布関係を使って,最終的な粒子の中心値を求めるようです.それが次の図になります.
- ちなみに,gmapping がラップしている「OpenSLAM gmapping」のコードを読むと,スキャンマッチングで中心計算が終わっているように見えたのですが….十分実効性があるから以降の計算を省いているということなのか?真意はよく分かりません.間違いだったらすみません.とりあえず先に進みましょう笑.
- まず,総和の区間に注目です.実は,総和を取る区間は「ある程度尤度が大きいものに限る」という割りきった決め方をしています.どうせ小さい尤度の粒子に関する項はほぼゼロなので,計算コスト削減のために省略したって構わないのです.
- そして,目標分布を近似計算するために,上記区間内の粒子を使って「事後分布=尤度☓事前分布」の形に則って中心と分散を計算します.条件にx_t-1があるので,事前分布の確率密度関数も出てくるのです.
- 粒子が尤度の高い領域に程よく撒かれていないと精度が出ないので,そこは理解をしておく必要があると思います.
重みでの変更点について
ここでのミソも,「地図」が周辺化されたままであることでしょう.あとは先に述べた総和区間内の粒子を使った事前分布を考慮して,重みを計算するのです.格子ベースでは重みの分散は敢えて計算する必要はないのですが(特徴ベースではカルマンフィルタの計算上必要となる),特徴ベースと比較する上で敢えて書くならこうなるだろう,という位置づけの書き方をしました.ただ,粒子で力づくで分布を近似しているので,分散を写像する非線形関数は不明です(不要ですが).
重みについては提案分布に比べればシンプルです.
ここでの説明は以上となります.
おわりに
如何でしたでしょうか.数式ごちゃごちゃなイメージのSLAMも,何となく直観的,感覚的に掴めるようになると,途端に親近感が湧いてきます^^
簡単におさらいです.本稿では以下の様な流れで,イラストと主要な数式を使って各SLAM手法の比較を行いました.
- 特徴ベースFastSLAM 1.0 → 特徴ベースFastSLAM 2.0
- 提案分布で観測情報を使うこと,重みで動作モデルの情報を使うことがミソでした.
- 特徴ベースFastSLAM 2.0 → 格子ベースFastSLAM 1.0
- 地図種別の違いのため地図情報を出すことを辞めたこと,提案分布の中心値を粒子の分布によって求めていることが主な変更点でした.
異なる文献を扱ったり,同じ文献でも情報が離れたりしていると何がどう変わったのかがうまく理解できないことが良く有りますが,それを全部持ってきて横に並べると何となくでも違いが見えてきて,爽快感を感じます^^
もちろん個人の解釈なので誤りが含まれるかもしれません.何か後で気づいたことがあれば,修正するようにします.
さて,次回以降,このFastSLAMを支える根本的な理論背景について解析していきます.なぜ「Rao-Blackwell化」なんてことをするのか?FastSLAMでは「完全SLAM問題」と「オンラインSLAM問題」を同時に解くということらしいが,実際の動作と対応させたときの意味付けはどうなるのか?
参考文献
- ROS Wiki.
- S Thrun, et al., "Probabilistic Robotics", the MIT Press, 2005.
- Grisetti, Giorgio, Cyrill Stachniss, and Wolfram Burgard. "Improved techniques for grid mapping with rao-blackwellized particle filters." IEEE transactions on Robotics 23.1 (2007): 34-46.
- "ros-perception/slam_gmapping", github.
- "gmapping", OpenSLAM