はじめに
カルマンフィルタは逐次ベイズフィルタの一種で,かつてのアポロ計画や,現代ではカーナビ等の身近な製品でも広く活用されています.モデルが線形である(あるいは線形に近似できる)ことや,ノイズがガウス分布に従うことを仮定する必要がありますが,その仮定が許容できるシステムでは実効性が高く,様々な場面で既に実用化されています.
そんなカルマンフィルタの式や,その導出を初めてみた時,こんな風に感じました.
「なんか,よく分からんが,複雑そうだなぁ」
だって,こんなんですもの...
- 状態空間表現(動作モデル,観測モデル)
\boldsymbol{x}_t = \boldsymbol{A} \boldsymbol{x}_{t-1} + \boldsymbol{B} \boldsymbol{u}_{t} + \boldsymbol{\epsilon}_t \\
\boldsymbol{z}_t = \boldsymbol{C} \boldsymbol{x}_{t} + \boldsymbol{\delta}_t
- 予測ステップ(事前推定値,事前誤差共分散)
\hat{\boldsymbol{x}}_t^- = \boldsymbol{A} \hat{\boldsymbol{x}}_{t-1} + \boldsymbol{B} \boldsymbol{u}_{t} \\
\hat{\boldsymbol{P}}_t^- = \boldsymbol{A} \hat{\boldsymbol{P}}_{t-1} \boldsymbol{A}^T + \boldsymbol{\Sigma}_\boldsymbol{x}
- フィルタリングステップ(カルマンゲイン,事後推定値,事後誤差共分散)
\boldsymbol{K}_t = \hat{\boldsymbol{P}}_t^- \boldsymbol{C}^T(\boldsymbol{C} \hat{\boldsymbol{P}}_t^- \boldsymbol{C}^T + \boldsymbol{\Sigma}_\boldsymbol{z})^{-1} \\
\hat{\boldsymbol{x}}_t = \hat{\boldsymbol{x}}_t^- + \boldsymbol{K}_t(\boldsymbol{z}_t- \boldsymbol{C} \hat{\boldsymbol{x}}_t^-) \\
\hat{\boldsymbol{P}}_t=(\boldsymbol{I}- \boldsymbol{K}_t \boldsymbol{C}) \hat{\boldsymbol{P}}_t^- \\
当初は,大群が押し寄せてきた感じがしました.
それでもなんとか,式を追っていけばこの形になるという事実は理解できたのですが,背後で何が起きているのかよくわからないと思っていました.
そこで,超シンプルなモデルを対象に,何が起きているのかイメージできることを目標に,私の考察を記述します.最もシンプルな例で解釈を進められるように,本記事で考察の対象とする信号は全て1次元とします.
備忘録ということで,変数等を全て厳密に定義しているわけではありません.ご容赦ください.
パーティクルフィルタに関する関連記事
関連項目として,パーティクルフィルタの点推定に関する考察も記述しておりますので,ご興味があればご参照下さい.
状態空間と観測空間が同一の場合
つまり,観測した信号がそのまま状態空間と同じ種類の信号を提供してくれる(観測方程式についてc=1),シンプルなモデルです.パラメータは全て1次元です.ノイズは全てガウス性を有するものとします.
定義
- 状態空間表現(動作モデル,観測モデル)
{x}_t = a x_{t-1} + b u_{t} + {\epsilon}_t \\
{z}_t = {x}_{t} + {\delta}_t
- 予測ステップ(事前推定値,事前誤差共分散)
\hat{x}_t^- = a \hat{x}_{t-1} + b u_{t} \\
\sigma_{\hat{x}_t^-}^2 = a^2 \sigma_{\hat{x}_{t-1}}^2 + b^2 \sigma^2_x
- フィルタリングステップ(カルマンゲイン,事後推定値,事後誤差共分散)
{k}_t = \frac{\sigma_{\hat{x}_t^-}^2}{\sigma_{\hat{x}_t^-}^2 + \sigma_z^2} \\
\hat{x}_t = \hat{x}_t^- + k_t (z_t - \hat{x}_t^-) \\
\sigma_{\hat{x}_t}^2 = (1 - k_t) \sigma_{\hat{x}_t^-}^2 \\
実は,誤差分散の文字の添字を上述のように表現することが一般的なのかまでは調査出来ていません.しかし,以後の説明で分散が重要になるので,全体として統一した表現になるようにするために,今回はこのような表現にしました.
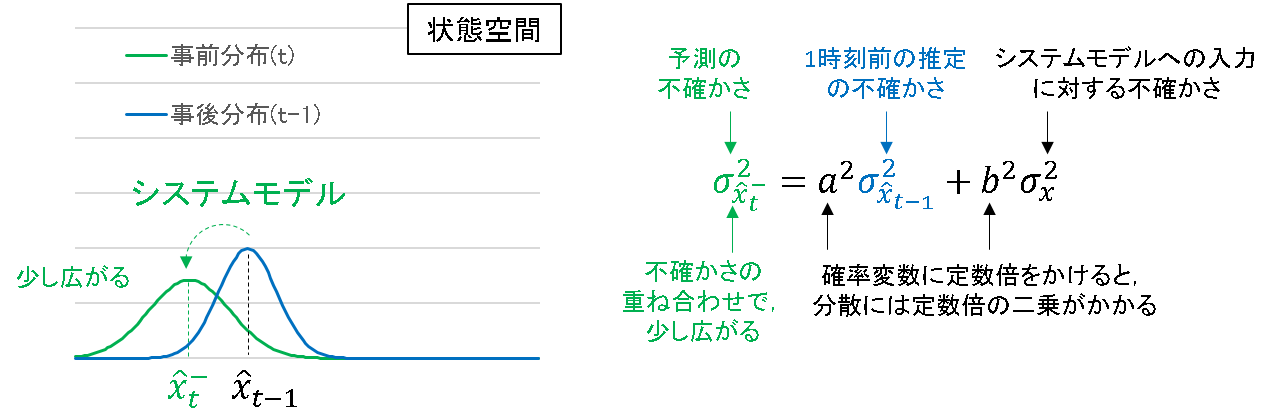
予測ステップについて
予測ステップでは,一時刻前の事後推定値からシステムモデルを元に事前推定値を算出します.これはただシステム方程式に代入すればいいだけです.
分散のところが少しごちゃついていますが,結論としては,
- 事前誤差分散 = 1時刻前の事後誤差分散 + システムモデルのノイズの分散
となります.
システムモデルで考えられうる不確かさを全て重ねあわせたものが,事前誤差分散となっていることが分かります.普通は,予測ステップで分散が広がります.システムへ入力が加えられると不確かさが増しそうな予感はします.
例えば,ロボットに速度指令を入力しても,ピッタリその通りに動くことはなく,必ずずれが生じます.
フィルタリングステップについて
予測ステップで得られた事前推定値に対して,観測情報を元に修正を加えます.
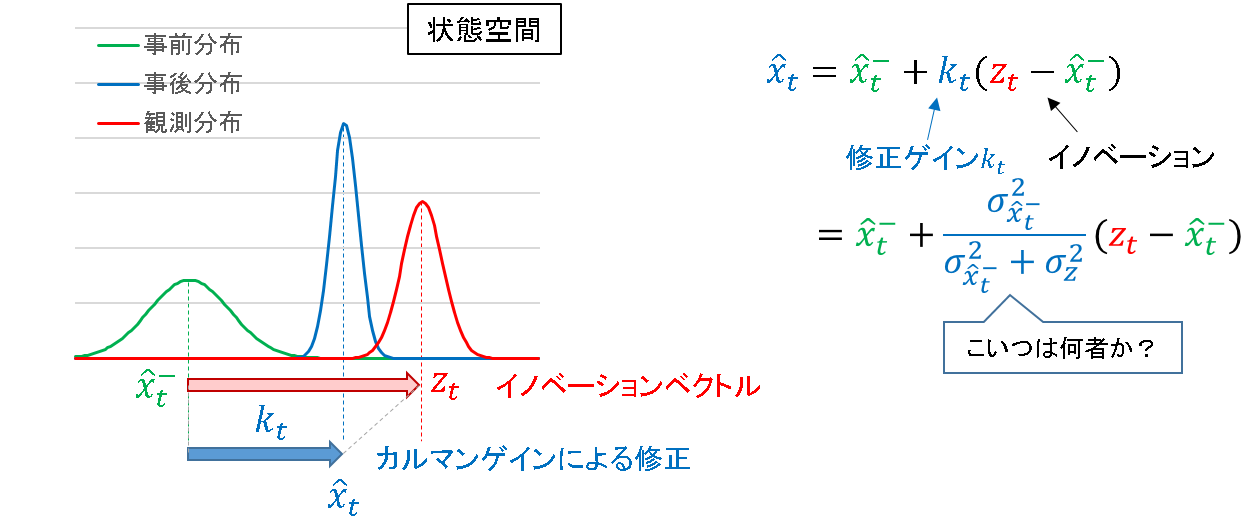
推定値
事前推定値と観測値の差分,すなわち観測予測誤差をイノベーションベクトルと定義し,これにカルマンゲインをかけることで修正量を決定します.
ここで気になるのは,カルマンゲイン
{k}_t = \frac{\sigma_{\hat{x}_t^-}^2}{\sigma_{\hat{x}_t^-}^2 + \sigma_z^2} \\
の意味です.分散の比を取っているようですが,ただ眺めているだけではイメージが湧きません.そこで,次のように考えてみます.
事後推定値は,事前推定値と観測値の内分点であり,内分比は k:1-k (0<k<1) であるとします.内訳は,下図を参照ください.
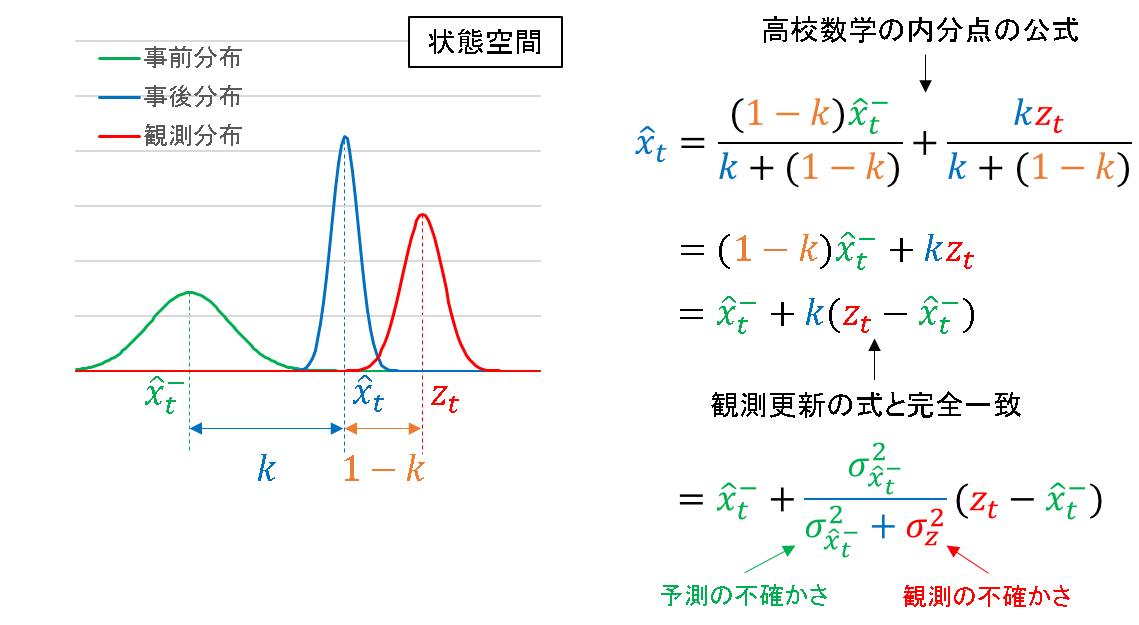
あとは高校数学で習った内分点の公式に代入すると,その計算結果がカルマンフィルタの事後推定値の更新式と一致することが分かります.
これにより,カルマンゲイン k の正体は事前推定値と観測値の何らかの指標に基づいた内分比であることが確認できました.そして,その内分比を決めるのが,それぞれの分散の大小関係であることも併せて理解できます.
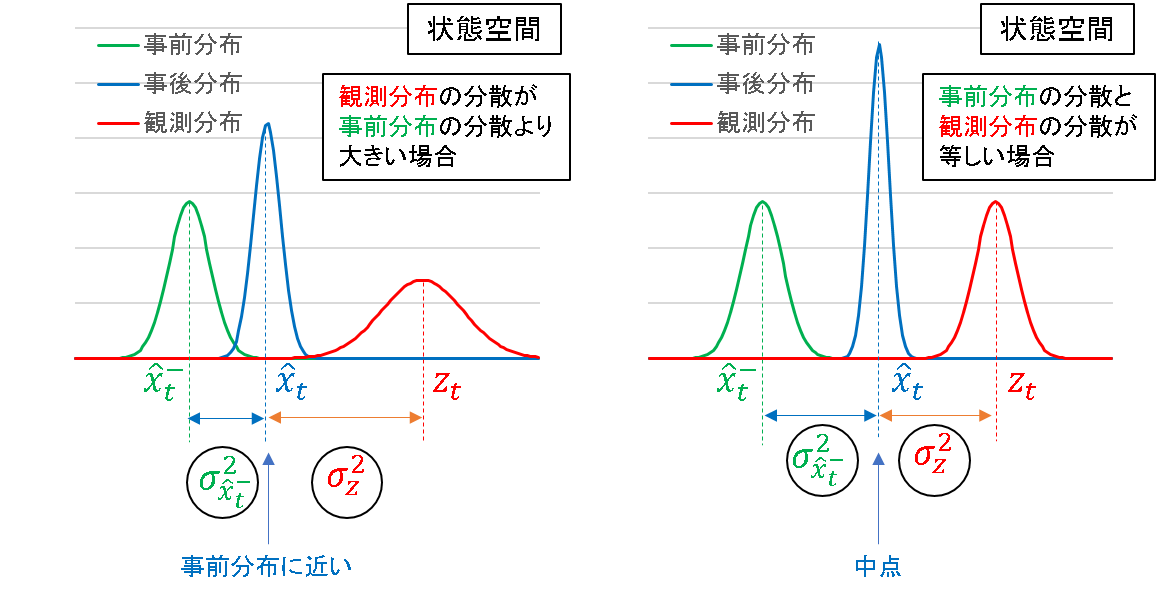
例えば先に示した図では,事前分布の分散が大きい(観測分布の分散が小さい)ので,修正量が大きくなり,観測に近い事後推定値を算出します.この観測の分散をさらに小さくすると,事後推定値はより観測値側によることになります.
一方,観測の分散の方が大きいとしたら,事後推定値は事前推定値側に引っ張られることになります.また,事前分布と観測分布の分散が一致するとしたら,事後推定値はちょうどそれらの中点を指すことになります.
敢えて例えるならば,事後推定値を求める際に,事前分布と観測分布は互いに綱引きをしており,その引きの強さが分散の逆数というイメージです.より分散の小さい方(すなわちより情報が確からしい方)が強く引っ張る力を持つということは,直観的にも正しい特性と言えます.
分散
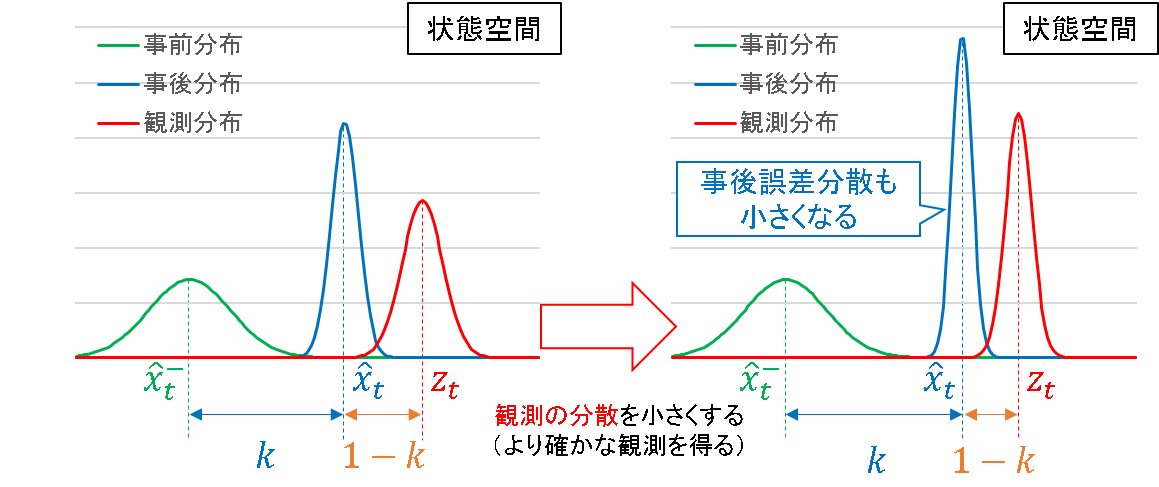
事前誤差分散に 1-k をかけることで,事後誤差分散を算出します.つまり,事後誤差分散は必ず事前誤差分散よりも小さくなります.これまで示した図中でも,それは確認できます.直観的には,推定に必要な情報が複数得られたので,より自信をもって答えることができる,といったイメージです.
更にいうと,追加で得られる観測情報が,事前の予測情報よりも確かであるほど分散が小さくなります.その度合を示すのが 1-k であり,これは事前分布と観測分布の分散同士の競合関係を表すので,直観的な解釈とも一致します.
状態空間と観測空間が異なる場合
次に,状態空間と観測空間が異なる場合を扱います.つまり,状態空間と観測空間の間に写像が存在する場合です.一応,簡単のためこれらの空間の写像が全単射であることを仮定します.(ここでは1次元なので,cが0でも∞でもなければOK.)
定義
- 状態空間表現(事前推定値,事前誤差共分散)
{x}_t = {a} x_{t-1} + {u}_{t} + \epsilon_t \\
{z}_t = c {x}_{t} + \delta_t
- 動作予測(事前推定値,事前誤差共分散)
\hat{x}_t^- = a \hat{x}_{t-1} + b u_{t} \\
\sigma_{\hat{x}_t^-}^2 = {a}^2 \sigma_{\hat{x}_{t-1}^-}^2 + b^2 \sigma^2_x
- 観測更新(カルマンゲイン,事後推定値,事後誤差共分散)
{k}_t = \frac{c \sigma_{\hat{x}_t^-}^2}{c^2 \sigma_{\hat{x}_t^-}^2 + \sigma_z^2} \\
\hat{x}_t = \hat{x}_t^- + k_t (z_t - c \hat{x}_t^-) \\
\sigma_{\hat{x}_t}^2 = (1 - k_t c) \sigma_{\hat{x}_t^-}^2 \\
予測ステップ
「状態空間と観測空間が同一の場合」と変わりませんので,省略します.
フィルタリングステップ
推定値
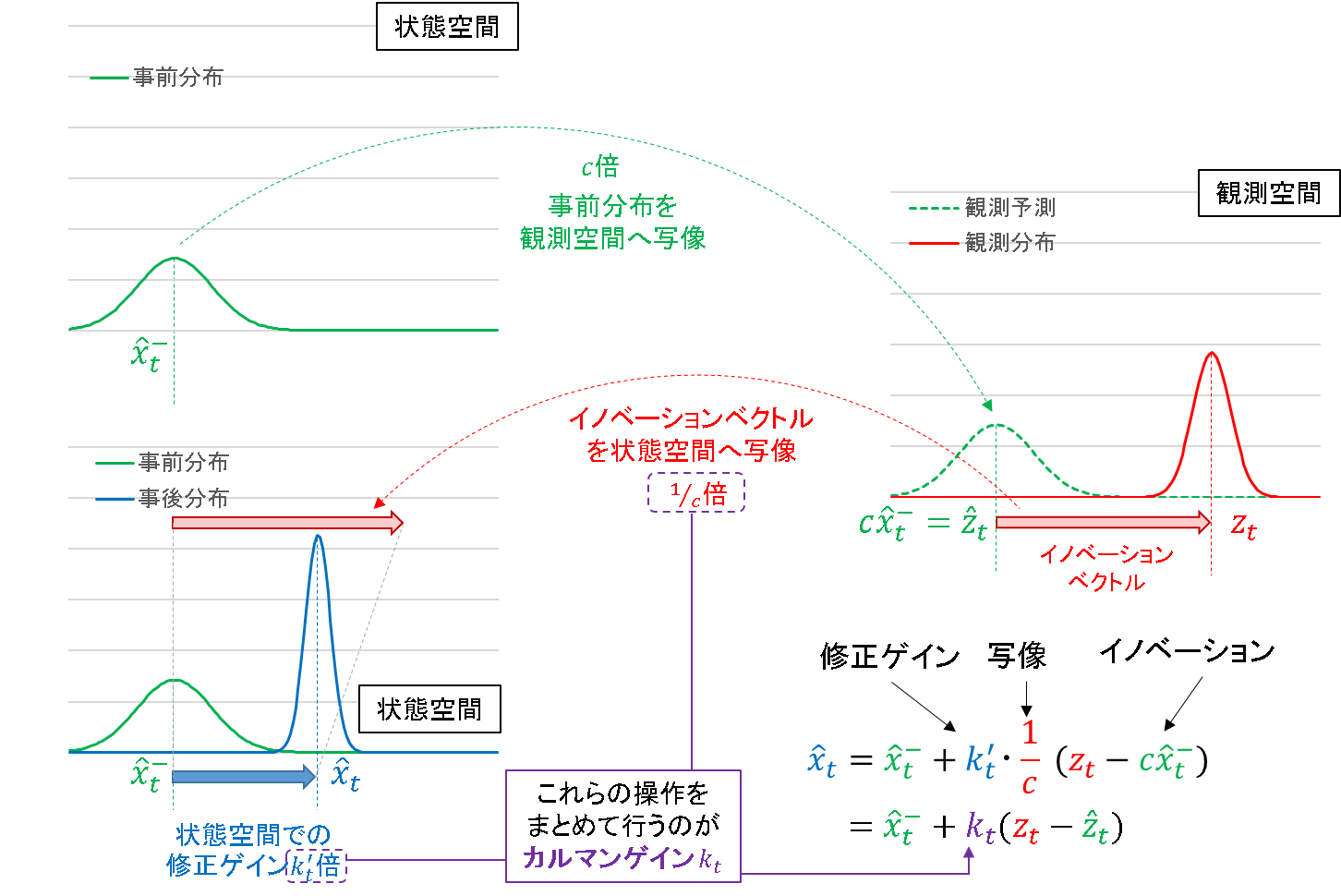
「状態空間と観測空間が同一の場合」では状態空間に関する一つのグラフで完結しましたが,ここでは観測空間に関するもう一つのグラフを用意してあげる必要があります.下図がそのイメージです.
先の場合と比べると,状態空間と観測空間を行き来している様子を確認できます.
- まず,事前分布を観測空間に写像します.(このとき写像によっては中心も分散も変わるのですが,説明のため同じ形のグラフを使っています.)
- 1 の写像を元に,観測空間内でイノベーションベクトル(観測予測誤差)を求めます.
- 2 で求めたイノベーションベクトルを状態空間へ写像します.
- 3 で写像されたイノベーションベクトルに,状態空間における修正ゲインをかけたものを,フィルタリングの修正量とする.
※今扱っている信号は一次元なので,イノベーション「ベクトル」と言うのは本当はまずいかもしれません…
短く言うと,フィルタリングステップとは,「観測空間のイノベーション」を「状態空間へ写像」したものに「修正ゲイン」をかけたもの,となります.このうち,「観測空間へ写像」と「修正ゲイン」をかける役割を同時に担うのが,カルマンゲインの役割と解釈できます.
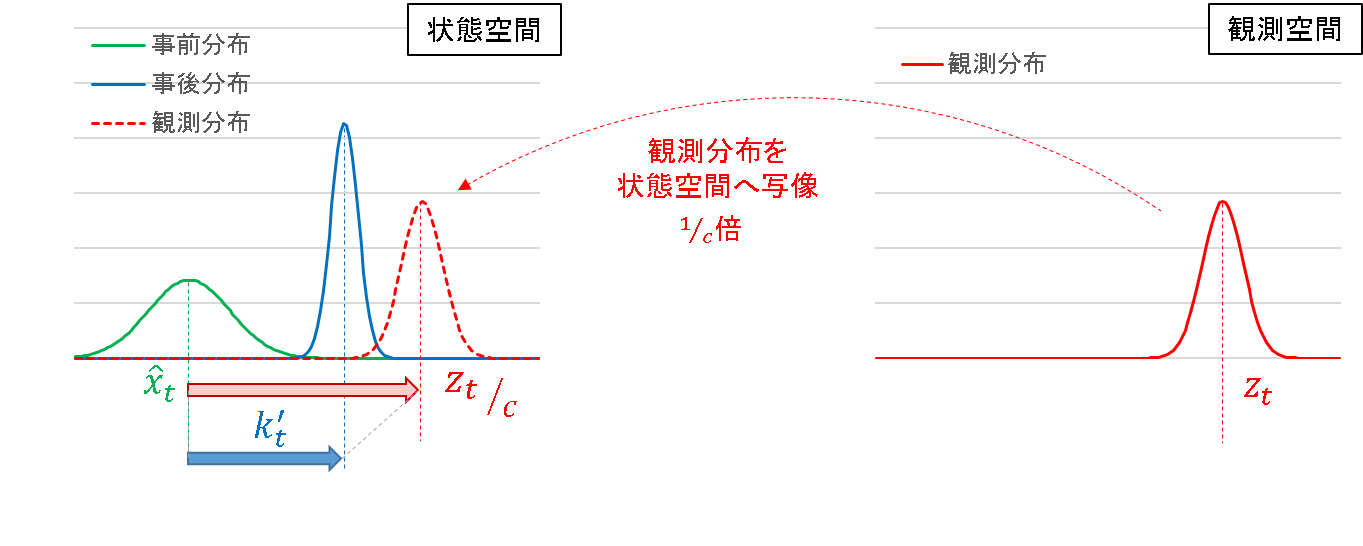
ここまでの記述でも性質は理解できるのですが,状態空間と観測空間を行き来するので,少しごちゃついたイメージは否めません.そこで,別の見方をしてみます.先に観測空間の信号を状態空間に写像してしまうという発想です.
こう考えると,以降は「状態空間と観測空間が同一の場合」と同様の流れで,シンプルに考えることができます.あとは,こんな考え方に変えても式が成り立つのか,というところです.
下図のように分解していくと,修正量が「状態空間での修正ゲイン」☓「状態空間での観測誤差」の形式に変形できることが確認できました.
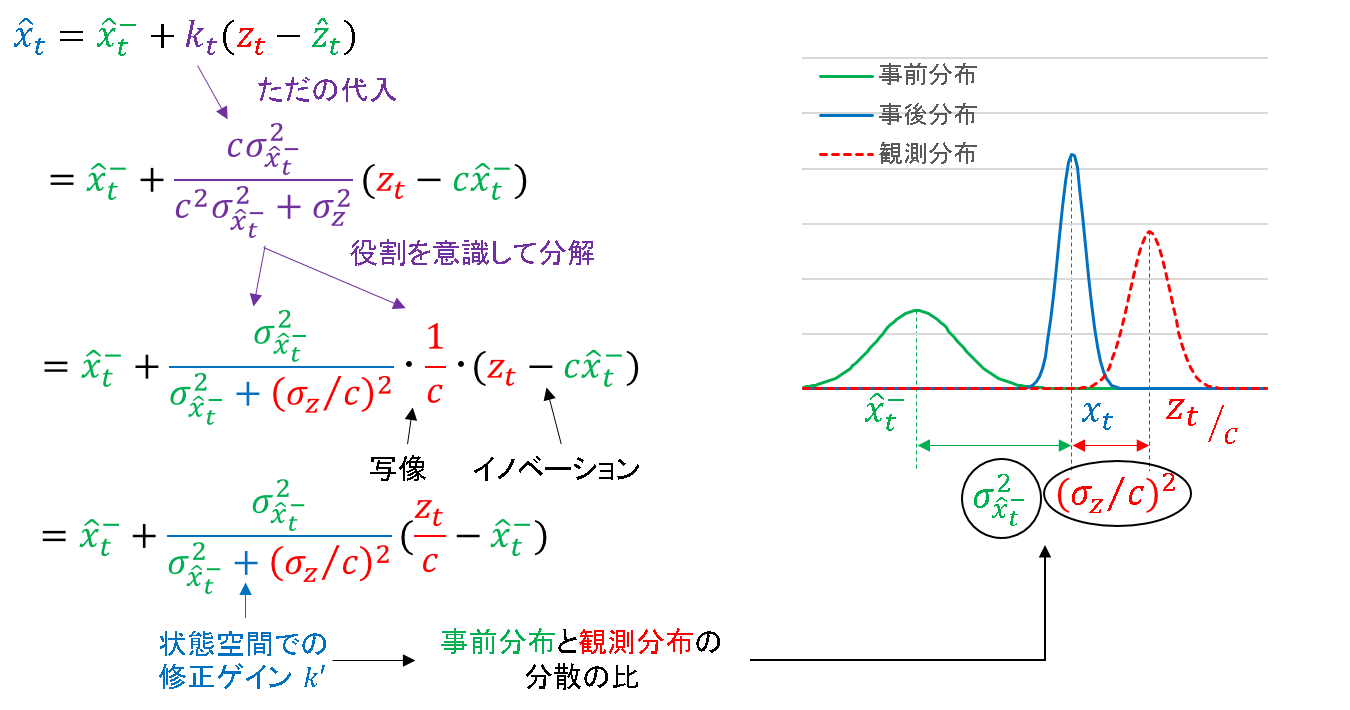
そして,修正ゲインk'はやはり「分散の比」となります.観測の分散がc^2で割られていますが,これは写像の結果を反映しているので,直観に反しない結果と言えます.
分散
残るは分散です.これも先の例と全く同様に議論できます.
ただし,c がかかっている点だけが異なりますが,これは状態空間という土俵に立たせるために必要な操作です.先ほど,
- 「カルマンゲイン」=「状態空間での修正ゲイン」☓「状態空間への写像(1/c)」
という関係を考えましたが,これを
- 「状態空間での修正ゲイン」=「カルマンゲイン」÷「状態空間への写像(1/c)」
- 「状態空間での修正ゲイン」=「カルマンゲイン」☓「観測空間への写像(c)」
に変形したものと考えられます.カルマンゲインには観測空間の値がかけられることになっているので,そこの整合性が合うような操作となっています.
多次元空間との類推
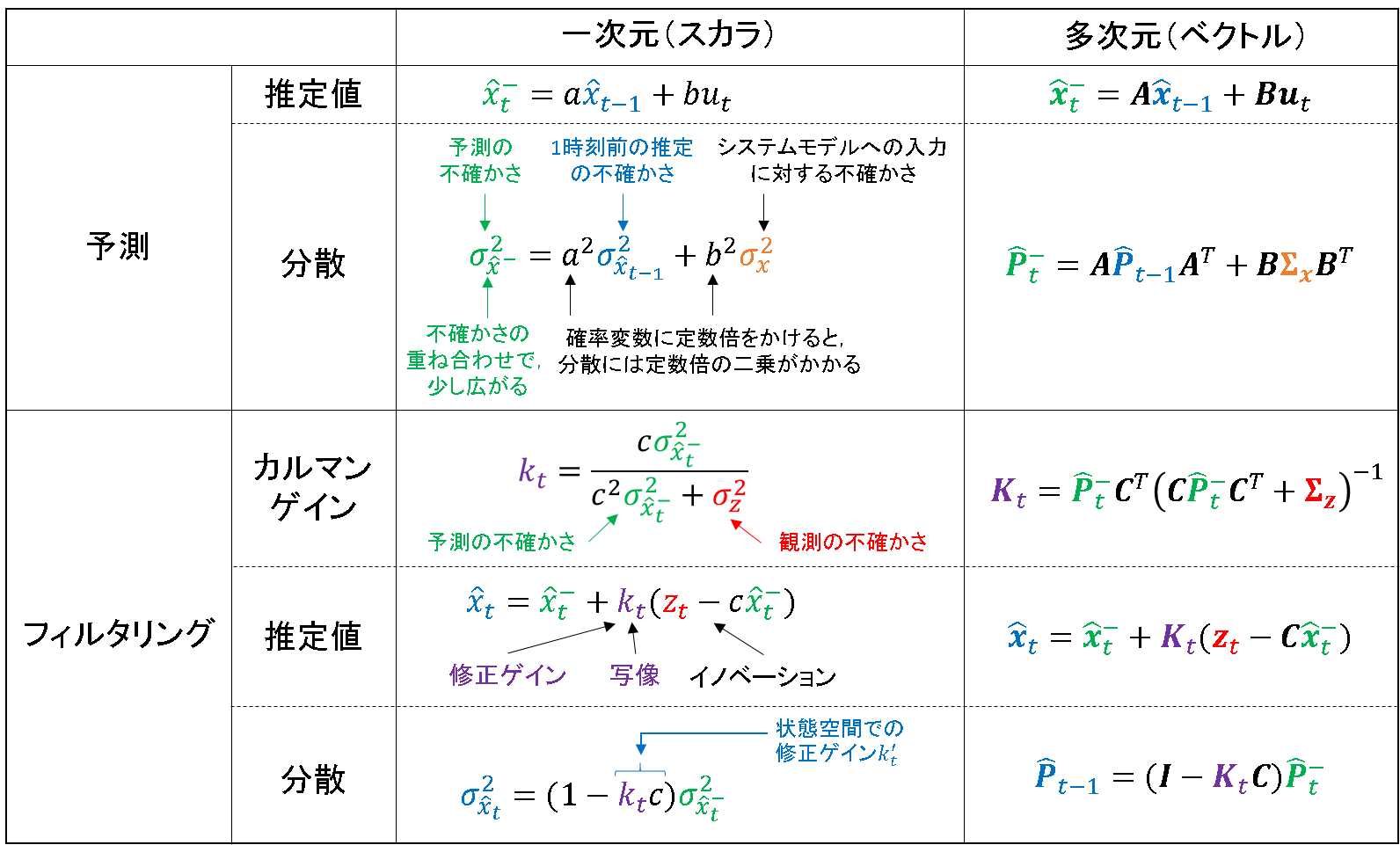
以上の解釈を元に,多次元のカルマンフィルタも同様に類推させることができます.下の表を眺めて左右の対応関係を比較すると,スカラの計算がベクトルの計算になっているだけ,ということが分かります.
2次元に展開した場合のイメージを例にすると,下記のようになります.
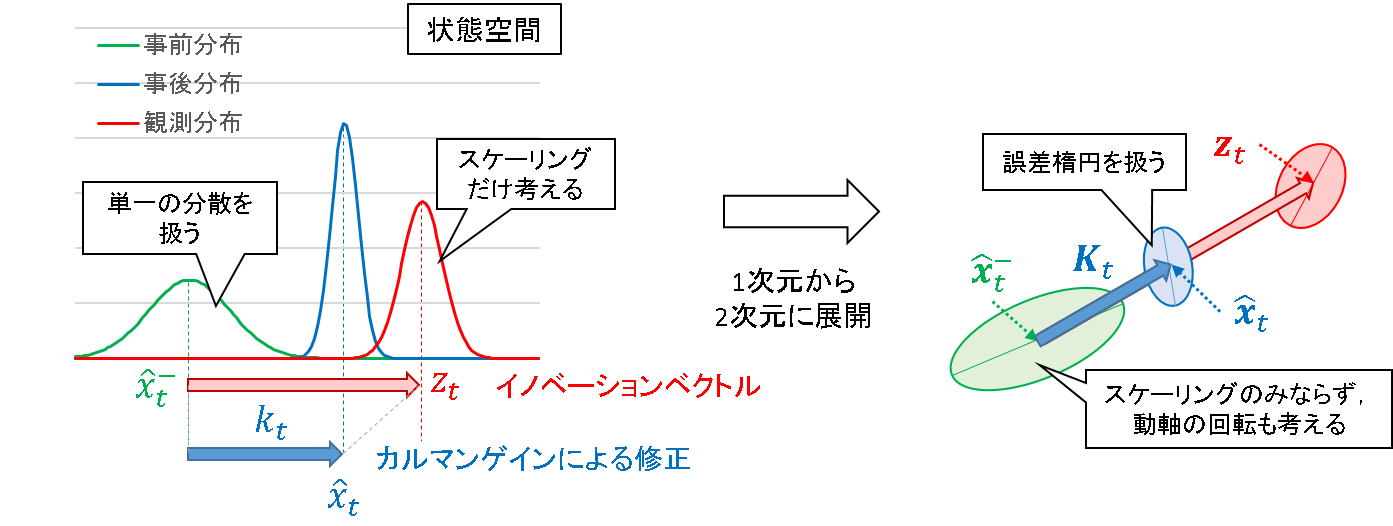
1 次元では,分散というスカラー値を扱えばよかったので,それがどれくらい大きくなるか,小さくなるか,というスケーリングだけ考えればことが足りていました.
2 次元の場合,誤差の生じる方向が2 つになるので,誤差楕円を考える必要があります.かつ,その楕円の動軸がどの方向を向くのかも,推定特性に大きく影響を与えます.この性質を評価するために,1 次元でいうところの「分散」が「分散共分散行列」に展開されていきます.
3次元の場合も同様の発想で,扱う図形が楕円体になるというイメージです.
それ以上の次元は幾何学的なイメージは困難ですが,本質的には同様のフローで展開されていきます.
おわりに
以上が,今回メモとして残しておきたかったことです.いくつかの参照資料を読みながら自分なりに考えることで,「式展開したらこうなった」から,何となくでも「背景にはこういう意味がある」という段階まで落としこむことができました.
数学を専門にしているわけでもない,しがなき素人学生の備忘録です.誤りもあると思いますので,ご容赦願います.その際は,厚かましくはございますが,ご指摘を頂けましたら幸いです.