目次
- 導入
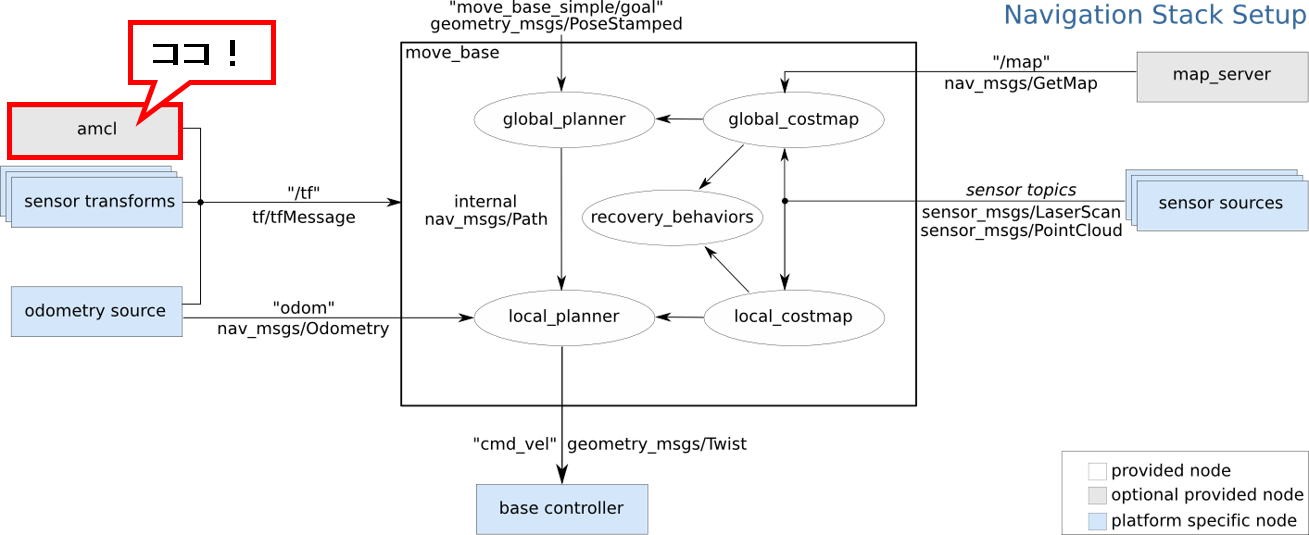
- move_base (ナビゲーション)
- ROSで遊んでみる
- ソフトウェア構成をみる
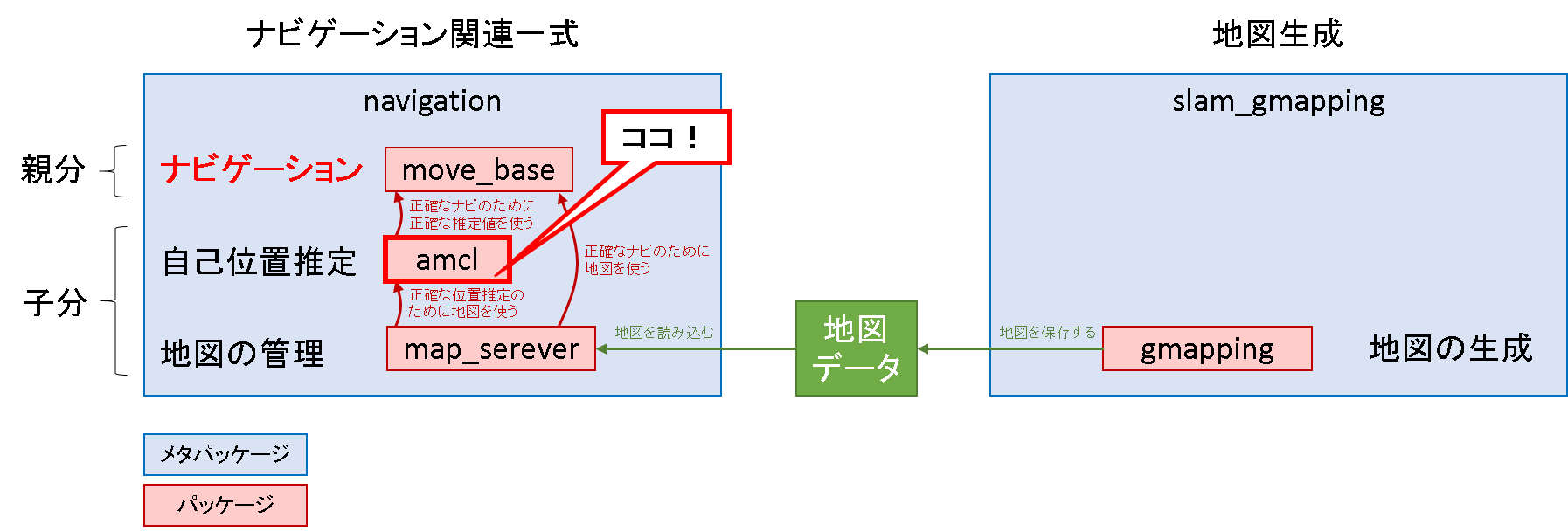
- amcl (自己位置推定)
- ROSで遊んでみる
- ソフトウェア構成をみる
- 原理をみる (準備編) ← いまココ
- 原理をみる (応用編)
- gmapping (地図生成)
- ROSで遊んでみる
- ソフトウェア構成をみる
- 原理をみる(応用編)
- 原理をみる(準備編 その1)
- 原理をみる(準備編 その2)
はじめに
Navigation Stack を理解する - 3.2 amcl: ソフトウェア構成をみるの続きです.大分間が空いてしまいました^^;
amclではパーティクルフィルタを活用した自己位置推定を行っています.その技巧的な特長をイラストに起こしながら,原理の一端を覗いていこうと思います.
なお,ROS Wikiによると,amclは adaptive Monte Carlo localization の略だとか.文献を読むと,確かに adaptive (適応的)というのは良い名前だと思います.
原理を見て行くということで,ROSとの触れ合いは少なくなります^^; ここでは,ROSで実装されているamcl内部の処理について,その動作の背後に潜む特性を直観的に読み取っていくとを目的としています.主な文献は,Probabilistic Roboticsです.
この記事を書くことは,私自身の理解を深めること,重要な概念は繰り返し登場させてでも定着を図ることも目的としています.記憶力の悪い私は,何度も同じことを繰り返してアウトプットしなければ,全然理解できないたちです.よって,記述内容は冗長で,文章は長いですが,これは意図的なものです.
このようなスタイルを好まない人もいると思います.これはひとえに私の力不足の産物ですので,ご容赦ください.一方,アメリカのテキストでは冗長な記述をすることは一般的なことであり,私自身はそのスタイルの書籍を読んだ方が結局早く理解できた,という経験があるので,あえて冗長性を排除するような記述はしないという選択もしています.
ですので,中身は知らなくてもいいからROSで遊べたら満足!っていう人は,飛ばした方がいいです^^
なお,amclの「原理をみる」コーナーは2部構成です.準備編と,応用編としています.準備編では,amclを理解する上で極めて重要なパーティクルフィルタの特性と,カルマンフィルタと比較しながら抑えていきます.応用編では,準備編で理解した特性をベースに,実際に自己位置推定をするときにどのようなフローを経るのかを,イラストを用いて理解していきます.
特徴ベースと格子ベース
自己位置推定を行う際,オドメトリだけだとずれが蓄積されて使い物にならなくなる,ということをNavigation Stack を理解する - 3.2 amcl: ソフトウェア構成をみるで話ました.
じゃあどうするのか?センサ情報を使います.どんなセンサ情報を使うのか?ということですが,この手の話でメジャーな方式として,特徴ベースと格子ベースがあります.amclでは,格子ベースを用いています.
それらのイメージを下図に示します.
特徴ベース(左側)
- ランドマークの特徴(形が違うとか,色が違うとか)とその位置が分かっているものとします.更に,ロボットのセンサからそのランドマークが観測できて,それがどの方向にどれだけ離れているのかが分かったとします.すると,そのランドマークから自己位置までの相対位置を計算できるわけです.
- でも,予めランドマークの特徴などを登録しておくという条件は,かなり強力な仮定となってしまいます.未知の環境で動作させるのは難しいでしょう.
格子ベース(右側)
- 目印となるものがランドマークではなく,任意の障害物となります.LRF(Laser Range Finder)やRGBDセンサ等で得られた情報を基に,障害物の有無を判定します.
- 空間をある大きさを持った「格子」の対にで分割しておき,障害物がある格子は塗りつぶし,障害物がない部分はオープンとする,といった方法で得られた言わば「ダンジョンゲームで使うような地図」と「センサ情報」とのマッチングを取りながら,自己位置推定を行っていきます.
- 特徴ベース法に比べると計算量は大きくなりますが,予めランドマークや特徴量を定義することなく利用することができるので,実環境で利用するならこちらの方が汎用性が高いと言えるでしょう.(上記格子を用いた地図を作る手間は発生しますが,わざわざ特別な特徴量を定義する必要がない点は利点と言えます.)
- このような地図を「占有格子地図」と呼びます.
amclでは格子ベースの自己位置推定行っているので,以降は格子ベースで議論を進めていきます.また,ここではSLAM(地図と自己位置の同時推定)ではなく,自己位置推定問題について記述してくので,地図は既に得られたことを前提にしています.
自己位置推定でパーティクルフィルタを用いるメリット
さて,amclでは自己位置推定にパーティクルフィルタを利用しています.計算量の小さいカルマンフィルタではなく,わざわざ処理の重たいパーティクルフィルタを使うのですから,それなりの理由があるはずです.
アプリケーション上の理由としては,「外乱に強い」に尽きると思います.なぜ外乱に強い推定ができるかというと,カルマンフィルタではノイズに「ガウス性」を仮定しなければならないのに対し,パーティクルフィルタではノイズに「ガウス性」を仮定する必要がないからです.
世の中,特に私たちの生活空間内には色々な外乱があるなかで,「ノイズは綺麗な一山だけだ!」というカルマンフィルタの仮定は,少々無理があると言わざるを得ません.もちろん,そういう仮定が十分通用するようなアプリケーションならカルマンフィルタを使うべきです.車のカーナビなんて,分かりやすい例と言えます.車が通るのは基本道路ですし,宙に浮いて追い越したりワープしたりはしません.それに,不測の事態が起きたら運転手の判断で車を止めてしまえばいいのです.また,アポロ計画にも拡張カルマンフィルタが使われていましたが,あれは宇宙空間の運動を想定していたので,比較的ノイズの仮定を簡易にしやすかったのでしょう.
一方で,私たちの実際の生活空間では,人が通行したり,障害物があったり,段差があったり,多様で複雑な妨害要素が紛れ込みやすいのです.したがってカルマンフィルタのように「全ての外乱はガウス性を有する」という強い仮定を置いてしまうと,これらのような外乱を考慮することが難しくなってしまうのです.
カルマンフィルタとパーティクルフィルタの比較
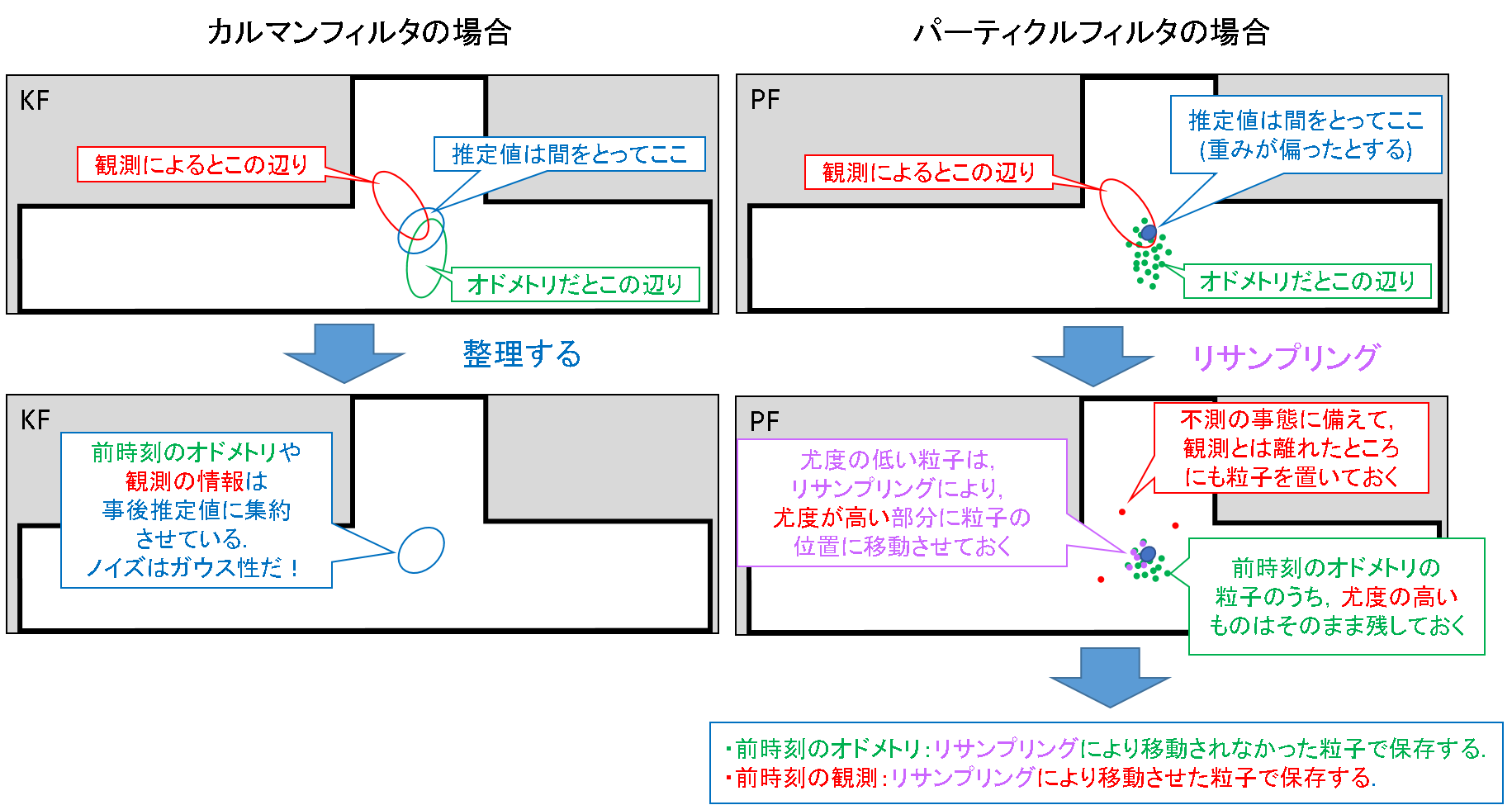
自己位置推定のアプリケーションを想定して,その特性の違いを図示すると,次のようになります.
カルマンフィルタ
- 事後推定値は,オドメトリ(事前分布)と観測(尤度)の間をとった値が算出されます.「間をとった」というのは乱暴な表現ですが,各分布のノイズにガウス性を仮定したときに最も「尤もらしい」値を解析的に求めた結果,間をとったような値になるのです.最尤推定や,最小二乗推定が該当します.
- 分散も同様の原理で,最もおさまりの良い値が算出されます.もちろん,ノイズはガウス性を有しています.
- このとき,オドメトリ(事前分布)と観測(尤度)の情報はすべて,事後分布の中心と分散の中に集約されてしまいます.言い換えれば,これ以降前時刻の事前分布と観測値の生の値は捨てられているのです.
- もしかしたら今の時刻だけたまたま大きなノイズが乗ってしまっていたり,たまたま障害物が出現してしまったがために,ガウス性のノイズに適合しないような観測値が得られてしまったとしても,そんなことはいざ知らず.単峰的なガウス性ノイズだけが混入していることを信じて,事後推定値と分散を算出してしまうのです.(ただし,観測がそれなりに信頼できるならば,何ステップかすると元の安定状態には戻れてしまいます.なんだかんだ言っても,カルマンフィルタでもそこそこ動くのです.)
パーティクルフィルタ
概要
- 一方,パーティクルフィルタでは事前分布と尤度の情報を完全には捨てないような配慮がなされており,かつガウス性から逸脱するようなノイズを考慮した仮定を置くことができます.
- 例えば,上図のようなオドメトリと観測の分布が得られたとして,かつ粒子のもつ重みに偏りが生じリサンプルも実行されると仮定します.
- 推定値を求める方法は,「最小二乗誤差推定(重み付き推定)」,「最大重み推定」,「最大事後確率推定(MAP推定)」等がありますが,ここではカルマンフィルタと比較するため,「最小二乗誤差推定」で,オドメトリと観測の間くらいに推定値が得られたとします.この推定方法は本質的にはカルマンフィルタと類似しております.この辺りの話は,以前小生が投稿した下記記事に記述しました.
- シンプルなモデルとイラストでカルマンフィルタを直感的に理解してみる
- なぜパーティクルフィルタの推定値に「重み付き平均」が使われるのかを考察してみた
直観的解釈
- さて,ミソはこの推定値が得られたあとの話です.代表的なものとして,リサンプリングと,ランダムサンプリングを図示してあります.
リサンプリング(重みによる)
- 事前推定粒子の残存(オドメトリ情報の保存)
- 粒子の重みがもともと大きい部分は,そのまま残存させておきます(緑の粒子).この粒子は,最小二乗推定で得られた位置とは異なる部分に位置していますが,この情報を捨てたりはしません.最小二乗推定値よりも確率は低いけど,まだそこが真の位置である可能性を否定できない!という立場で,敢えて残しておくのです.これが,カルマンフィルタと決定的に異なる特性の一つです.これにより,前時刻のオドメトリの情報を以降の推定のために保存することができます.
- 観測による粒子の移動(観測情報の保存)
- 重みが小さい粒子は,どうするのか?重みが大きい粒子の位置まで移動させてしまうのです.オドメトリだけをしていくと,どんどん粒子の分布が広がっていってしまい,とてもありえないような位置にまで粒子がばら撒かれたら,無駄な計算をしなければなりません.
- そこで,尤度を利用するのです.観測によって算出される尤度だって無視はしません.上述したような無駄な計算をする状況になってしまうくらいだったら,観測した結果から判断してより確からしいと思われる位置に多数の粒子を撒いておく方が,推定の効率が良いのです.これにより,前時刻の観測情報を以降の推定のために保存できます.
- 粒子の残存と移動のバランス
- ただし,あまり頻繁にリサンプリングをさせすぎると粒子の多様性が失われてしまいます.せっかくガウス性ノイズを仮定しなくてよくなり,不測の事態にも対処しやすいという特性を持つのに,それをみすみす潰してしまうことになりかねません.
- つまり,バランスが重要です.あまりに広い範囲に粒子が分布してしまっても無駄が多くなるけど,かといって過度に観測ばかり信じて粒子の再配置ばかりをしても,今度はパーティクルフィルタが本質的に備えている多様的なノイズを考慮した特性が失われてしまうのです.
- したがって,どのタイミングで,どれだけ粒子を移動させるのかは,アプリケーション依存のチューニングパラメータとなります.まぁそれにしても,カルマンフィルタに比べたらノイズに強そうだ,という雰囲気がこの時点で感じられます.
ランダムサンプリング
- パーティクルフィルタの応用的な機構の1つです.詳細は応用編で取り上げます.
- いくら観測のノイズに「ガウス性」を仮定できるとは言っても,リサンプリングのたびにその多様性がすべてリセットされてしまいます.それに,ロボットの誘拐問題といったように,突然観測の想定外のところまでロボットが誘拐されちゃったときまでは想定できないのです.
- じゃあ,誘拐されていそうだと分かった時に,センサの標準的な分布を無視したランダムな位置にも粒子を撒いてしまえばいいではないか!という発想が出てきます.これがランダムサンプリングです.
- こういう風に,粒子のばら撒き方(状態推定の仮定)を,ある意味何でもあり的に扱えるのがパーティクルフィルタの強力な特性の1つです.単峰的なガウス性ノイズを仮定しているカルマンフィルタでは実現できない特性です.
amclにおけるパーティクルフィルタの利用
- amclでは,パーティクルフィルタのこのような特性を利用して,技巧的に定義された関数で尤度を計算しています.
- そこでは,綺麗な観測モデルに加え,特殊な外乱要素を混入させた外乱モデルを適用しています.
- その特殊な外乱として,ランダムな要素だけではなく,アプリケーション上考えられる想定可能な外乱も考慮したモデルが採用されています.後ほど,この点についてもイラストを使って説明していきます.
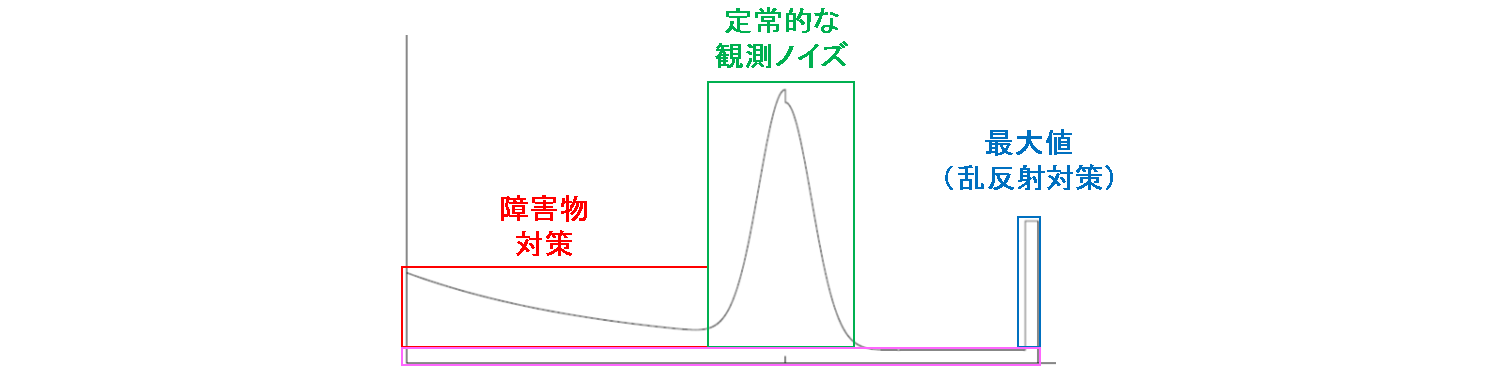
ベイズフィルタとの対応
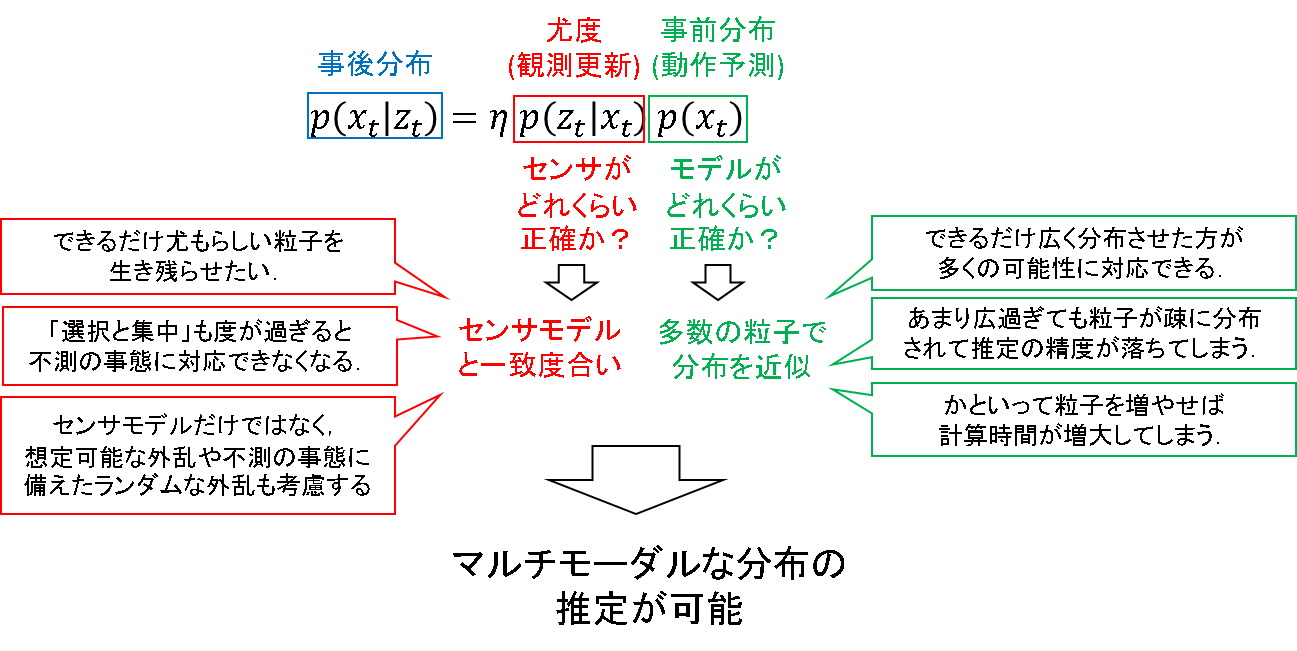
ここまでパーティクルフィルタについて話した内容を,ベイズフィルタの定式に対応させて解釈してみます.
必要な記述は上図に示しています.ガウス性ノイズだけではなく,様々な分布を混合させたマルチモーダルな分布の推定もできるのが,パーティクルフィルタの特長であることを頭に焼き付けておきます.
おわりに
本記事では,amclを理解する上で極めて重要であるパーティクルフィルタの特性を,カルマンフィルタと比較しながら理解することに焦点を絞りました.
つたない文章のくせに,文字が多くて退屈だったと思います.特性の説明の重点を置く以上,簡素なイラストに対して様々な視点から解釈をしていくことになり,文字が多くなってしまいました.これは,ひとえに私の甚だしい力不足に尽きるのですが....次の応用編ではもう少しイラストを交えていくことになります.
本記事での内容が退屈で仕方がなかった場合は,一度応用編を読んだ後に戻ってくると,もう少しすっきりと読めるかもしれません.
Next: 3.4 amcl: 原理をみる (応用編)
Prev: 3.2 amcl: ソフトウェア構成をみる