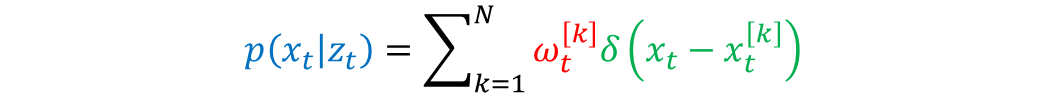はじめに
パーティクルフィルタは逐次ベイズフィルタの一種で,ロボットの位置推定や画像中の物体追跡等でよく使用されます.非線形なモデルや,非ガウス性のノイズが混入するシステムでも適用可能であるうえ,実装が容易であることから,広く使われているようです.
パーティクルフィルタは「分布」を推定する仕組みなので,実用上はただ一点の推定値(点推定値)を算出する必要があります.その方法として「重み付き平均」が一般によく採用されるようなのですが,ぱっと調べたり,論文を読んだりしてみても,天下り的に使われていることが多いようでした.
ところが,ど素人の私にはそれが当たり前とは思えませんでした.そこで,なぜ「重み付き平均」が妥当な推定値を算出するのかを理論的に意味づけしている文献を探したのですが,ぱっと調べたくらいでは見つけられなかったので,自分なりに考えてみることにしました.
前提として、パーティクルフィルタは分布を推定する方法論であり点を推定するものではない、そのため「点推定手法」として「重み付き平均」が用いられているが、これにはどんな意味があるのだろうと、リバース・エンジニアリングをした形式を取っています。したがって、一般的な帰結に至ることができていないままの記事になっておりますことを、お詫び申し上げます。
備忘録ということで,変数等を全て厳密に定義しているわけではありません.ご容赦ください.
カルマンフィルタに関する関連記事
関連項目として,パーティクルフィルタの点推定に関する考察も記述しておりますので,ご興味があればご参照下さい.
式展開と思考実験
ベイズ則
観測データが得られたときの事後分布は,ベイズ則により次のように与えられます.
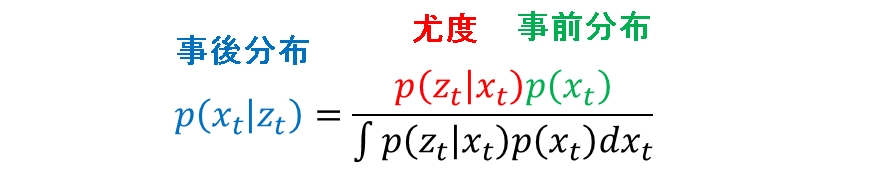
事前分布の近似
事前分布はN個の粒子群によって近似されているものとします.この分布をディラックのデルタ関数を用いて,次の経験分布で表現します.
これで,連続状態空間において,離散的な粒子の状態値を扱えるようになります.
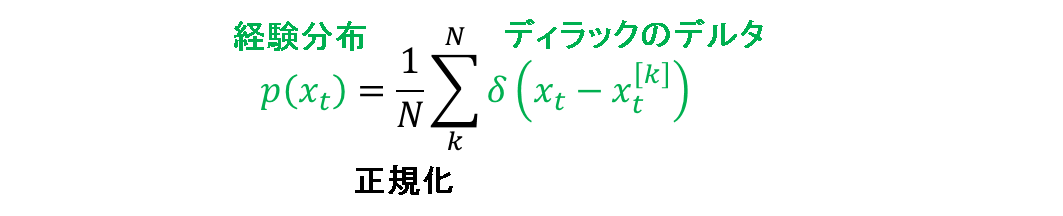
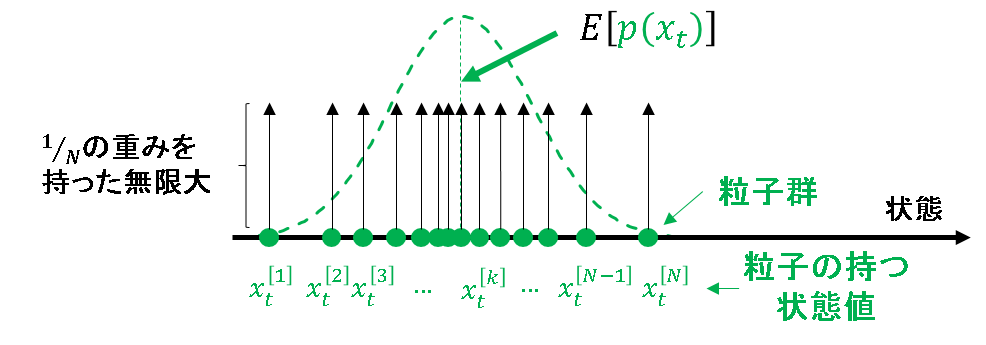
このイメージを,下記に示します.パーティクルフィルタなのでノイズにガウス性を仮定する必要はないのですが,ここでは説明のために事前分布はガウス分布に従うものとします.インデックスも順番に並ぶものではありませんが,簡単のため綺麗に並べているだけです.矢印は,無限大の長さを表します.
これを事後分布の式に代入します.粒子のもつ状態値でしか意味を成し得ない性質を利用しています.
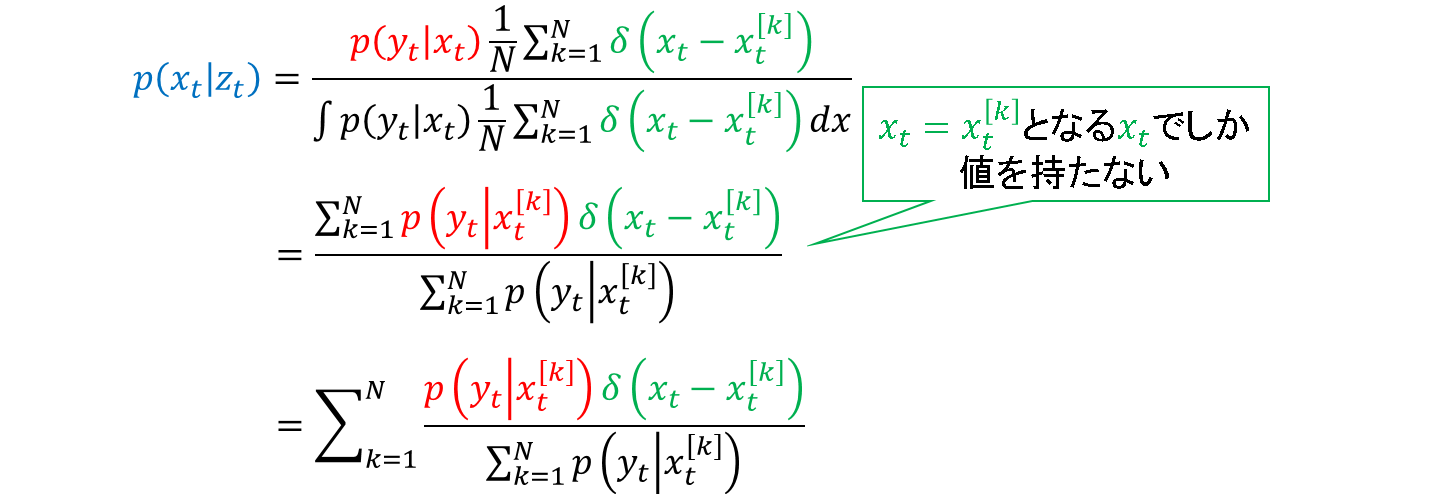
重みの導入
ここで,重みを次の式で与えます.全粒子について,尤度を正規化しているだけです.
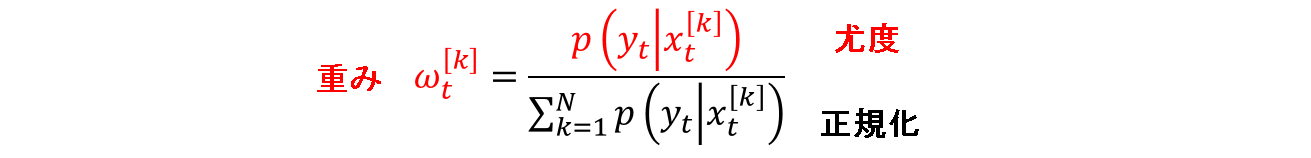
この重みを使って事後分布の式に代入すると,次のようになります.
各粒子が,ω分の重みもったスペクトルを形成するようなイメージです.
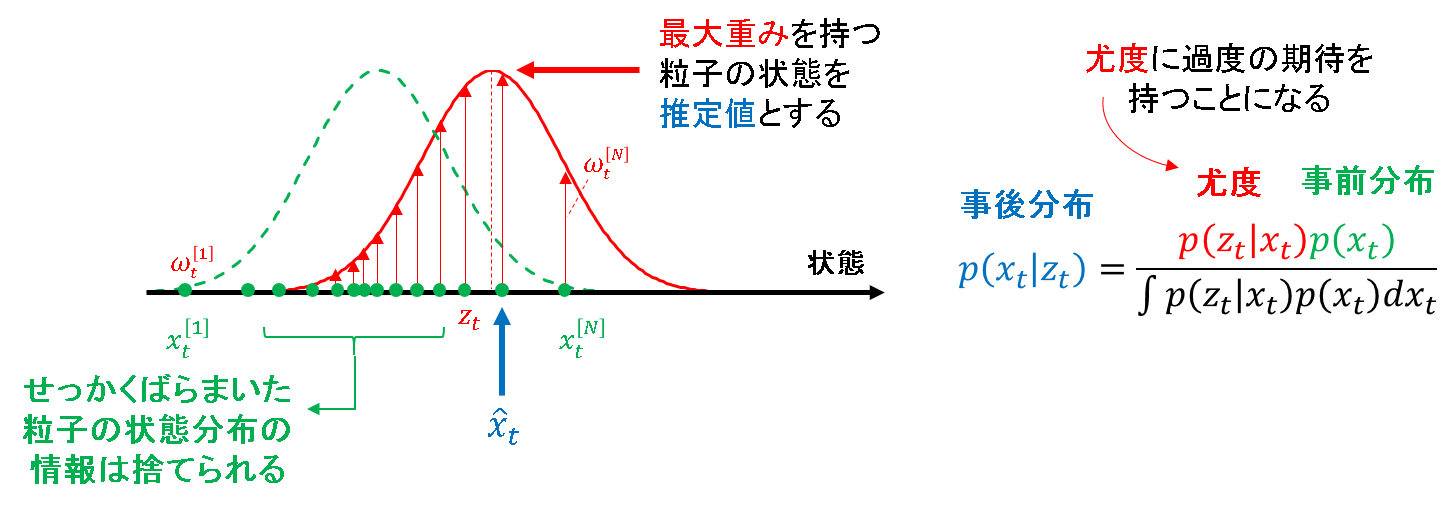
そのイメージを,下図に示します.なお,簡単のため状態空間と観測空間が同一(観測によって直接知りたい情報が得られる)と仮定します.また,こちらも簡単のため,尤度関数がガウス分布に従うものとします.
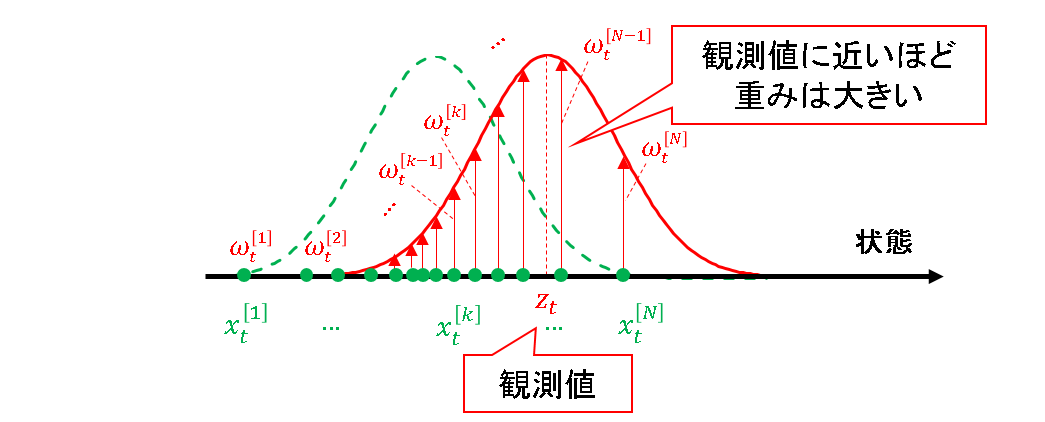
尤度をそのまま重みに当てはめているので,観測値に近い状態を持つ粒子ほど重みが大きくなる,という事実は至極当然です.矢印が出ていない粒子は重みが無いのではなく,小さすぎて尤度関数に合わせて描けないので省略しています.
説明のために挿入した図形を排除したものを再掲すると,下図になります.
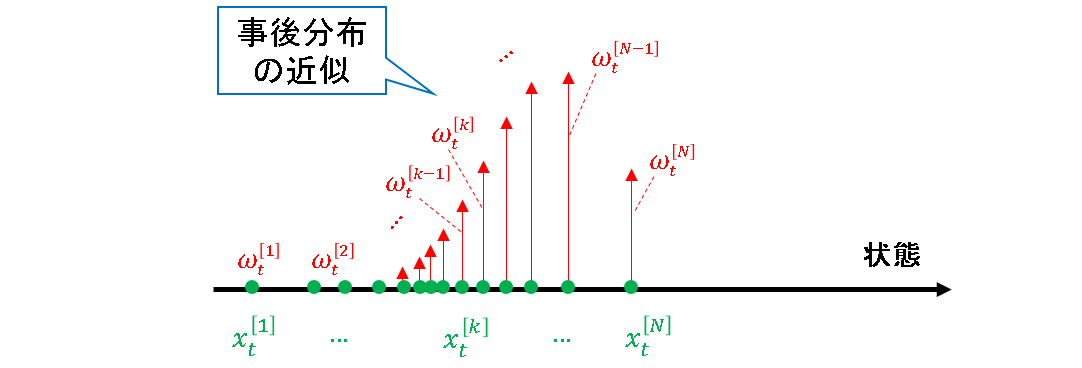
これが粒子によって近似された事後分布の素直な実体です.これだけながめていても,私的には「これが事後分布?」といった感触です.
ですが,パーティクルフィルタとはそう定義されたものです.背後には真の事後分布の形が存在するのでしょうが,それを解析的に計算出来ないから妥協してこのような形で近似しよう,という発想があります.
こうして得られた情報を元にどう推定値を計算するかは,実は利用者側に委ねられています.その手段の一つして,「重み付き平均」という方法が存在する,という位置づけです.
「重み付き平均」の話が出てきたところで,本題に戻ります.
事後分布の点推定値
ようやく本題に来ました.なぜ「重み付き平均」が推定値になるのか,というところです.
これまで説明のためにと,事前分布も観測分布もガウス性のノイズを有することを仮定してきました.ここでも天下り的に,事後分布にもこの仮定を適用してみます.
すると,ガウス分布に従う事後分布の期待値を求めることは,最大事後確率を持つ状態値を算出することと等価になります.これを計算してみます.
結果は,重み付き平均となりました.
つまり,事後分布がガウス分布に従う場合には,その最大事後確率推定値を重み付き平均によって算出できるということです.
この点について,もう少し考察を加えてゆきます.
考察
ノイズにガウス性を仮定した場合
事前分布と観測分布が与えられたところまで一旦話を戻します.
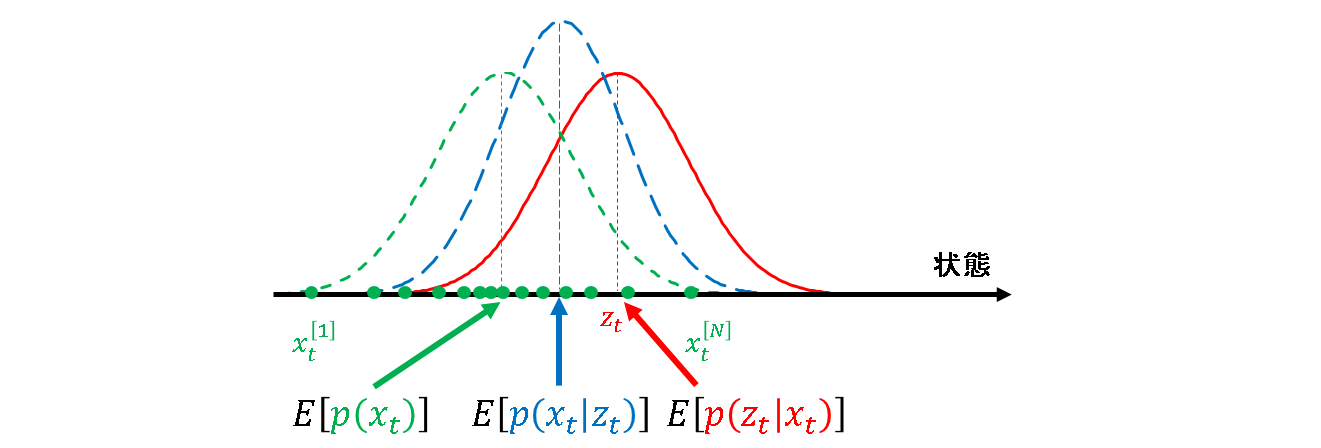
下図を参照ください.ざっくり言うと,「粒子数が多いけど重みが小さい領域」と,「重みが大きいけど粒子数が少ない領域」が存在することが見て取れます.
これは,カルマンフィルタでも見られる,事前分布と観測分布の分散による競合関係とのアナロジーと解釈できます.そこから類推すると,重み付き平均によって算出された事後分布の期待値は,事前分布と観測分布の間のどこかを指すことが想像できます.実際に計算しても,そのような値が算出されます.
今,事後分布を重み付きの粒子で近似している以上,その形状自体を把握する情報はありません.しかし,おそらく背後には上図に示したようなガウス性を有する事後分布が形成されていて,重み付き平均を求めることでその中心を算出しているという解釈になると思います.
事前分布と観測の競合関係についても,より分散の小さい分布の方に事後分布の期待値がよっていくことも容易に想像ができます.これも,カルマンフィルタのもつ性質とのアナロジーと言えます.
カルマンフィルタのもつこの性質については,小生が以前投稿したシンプルなモデルとイラストでカルマンフィルタを直感的に理解してみるに記載しました.
ノイズにガウス性を仮定しない場合
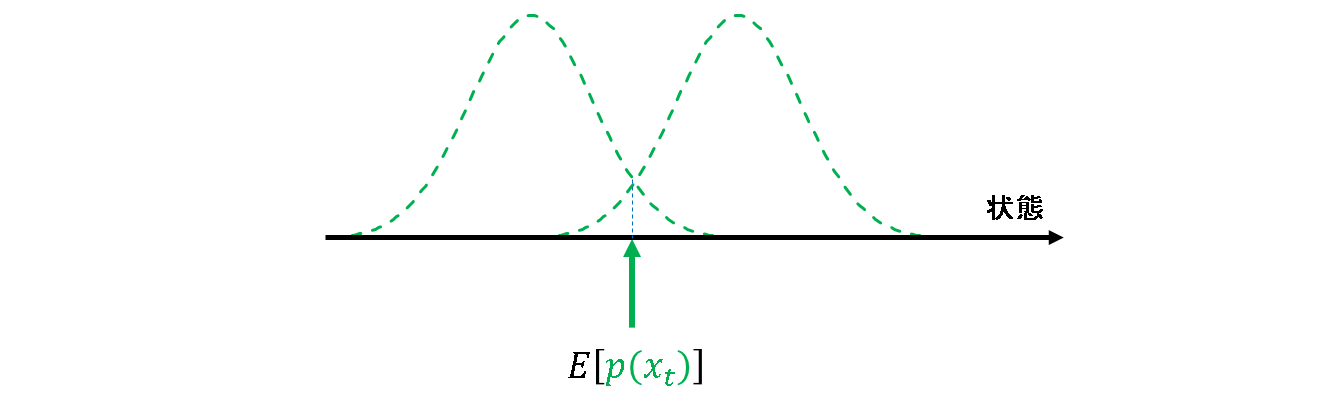
ところが,ノイズが多峰性を有していると,話は単純にはなりません.下図の例を見てみます.例えば,こんな事前分布が得られているとします.この分布に対して,期待値を求めると,峰と峰の間の事後確率が小さくなるような場所に推定値が算出されてしまいます.
重み付き平均を取れば少し観測側に寄った事後推定値が得られるでしょうが,そもそも事前推定値が妥当ではない期待値を元に算出されているので,当てになりません.
これは,システムモデルが非線形であったり,ノイズが非ガウス性であれば起こりうる話です.現実世界では様々な外乱が存在するため,こういうモデルを扱うことが多いので,何も考えずに「パーティクルフィルタの推定値は重み付き平均を使う!」という思想だと,実は危険です.
では実際はどうしているか?
実際には,「定常的なノイズとしてガウス性を仮定」しておいて,+αで「想定できるノイズ成分」や「不測の事態に備えたランダムなノイズ成分」を混合させたりしながら,ロバストな推定ができるのがパーティクルフィルタの特長です.
例えばProbabilistic Roboticsでは,パーティクルフィルタをロボットの位置推定に活用している事例が紹介されており,かなり技巧的に,しかし理論的な裏付けを持って丁寧にモデルが組まれていることを確認できます.これを一読すれば,パーティクルフィルタの実世界適用についての感覚が身につきます.その例だと,やはり重み付き平均は使っておらず,最大重みを使っているようです.
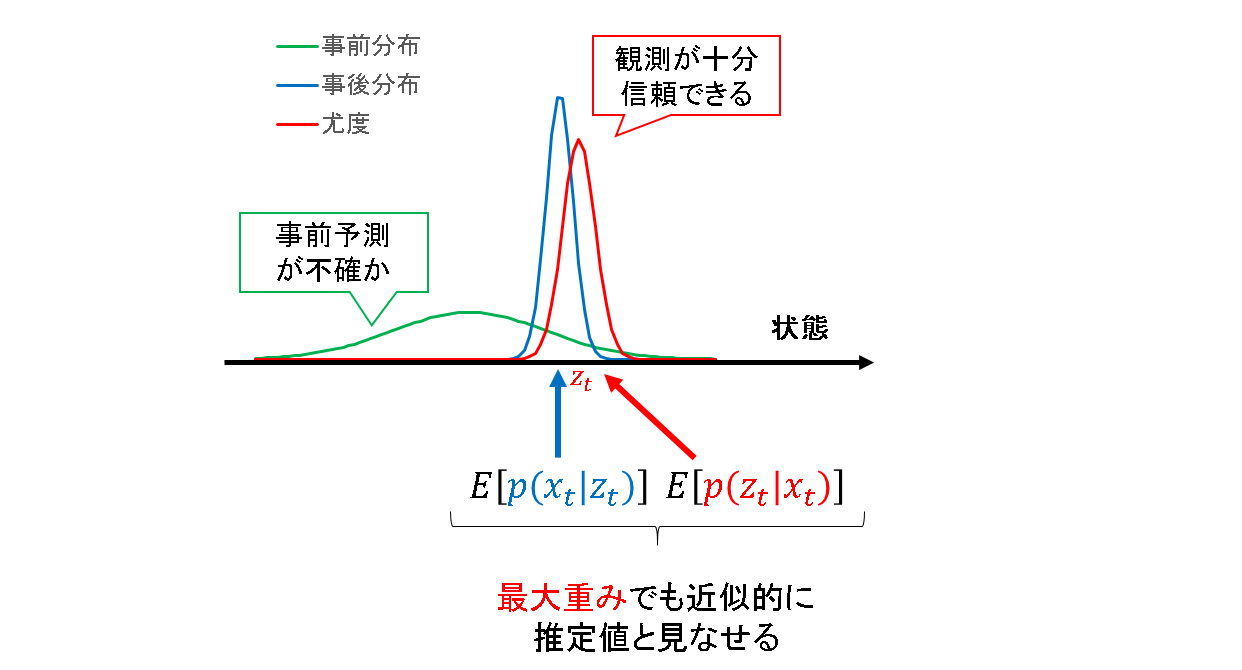
ただし,安易に最大重み推定を使うのもまた考えものです.推定値を求める指標が観測尤度のみとなるので,観測にノイズが乗ってもそのままそのずれを信じてしまう状況です.事後推定値だけを見れば,事前分布の情報はバッサリ捨てられてしまうのです.言い換えれば,理論的には事後確率の最大値とは何ら関係がなくなってしまいます.
したがって,最大重みを採用する際には,「事前予測よりも観測の方が十分に信用できる場合に,近似的に最大重み推定が利用できる」ということを理解しておく必要があります.例えば,ロボットの自己位置推定の場合だと,この仮定が成り立つ(オドメトリはずれまくるけど,レーザセンサやポイントクラウドはそんなに嘘はつかない等)ことが多いため,観測情報を信じることはそんなに悪い話ではない,という解釈です.
おわりに
パーティクルフィルタの点推定に重み付き平均が使えるのは,ノイズにガウス性が仮定できるという制約された状況に限られます.
ただし,その仮定が成り立つと見なせる場合なら,計算時間も少なく,十分な実効性をもって働くようです.
従って,何も考えずに「重み付き平均を使おう!」ではなく,それで許容できるシステムなのかを事前に考えてみると,良いかもしれません.